Л Е К Ц И Я 1 Числовые ряды 1
1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ Определение 1. Если каждому значению по определенному правилу или закону, ставится в соответствие некоторое действительное число , то множество занумерованных действительных чисел называется числовой последовательностью и обозначается символом . При этом числа называются членами последовательности, а выражение аn называется общим членом последовательности. 2
3
Определение 2. Последовательность называется возрастающей (убывающей) если: Определение 3. Последовательность называется ограниченной сверху (ограниченной снизу), если существует такое число М (число m), что 4
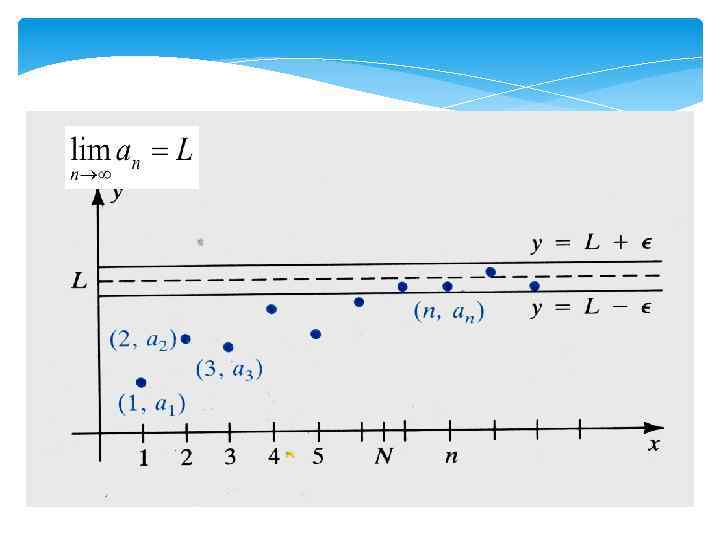
Определение 4. Последовательность называется ограниченной, если она ограниченна как снизу так и сверху, т. е. существуют такие числа М и m , что сл. A и пишут: Определение 5. Число L называется пределом последовательности если для сколь угодно малого положительного числа найдется такой номер зависящий от что для всех натуральных чисел выполняется неравенство 5
. 6
1. Понятие ряда и его сходимости Рассмотрим сл. числовую последовательность: 0, 6; 0, 006; 0, 0006; ……. В этой последовательности Построим сл. последовательность: : 7
Последовательность чисел называют последовательностью частичных сумм. Сумма бесконечной геометрической прогрессии. Бесконечную сумму называют числовым рядом. 8
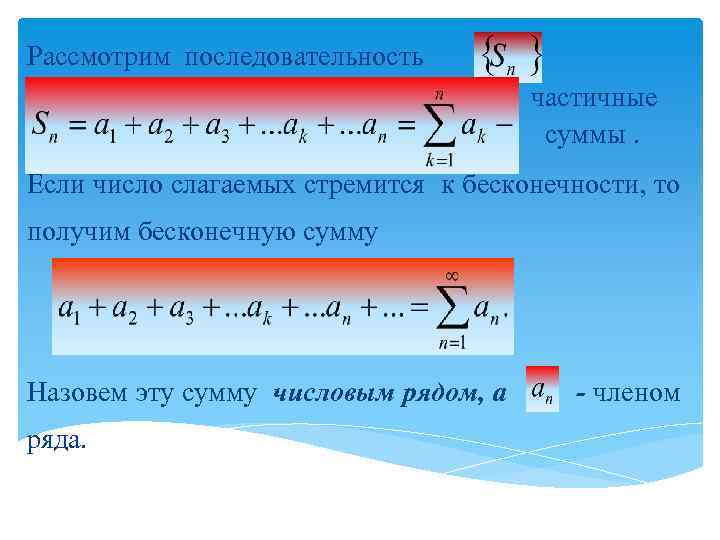Рассмотрим последовательность частичные суммы. Если число слагаемых стремится к бесконечности, то получим бесконечную сумму Назовем эту сумму числовым рядом, а - членом ряда.
Определение. Если существует конечный предел последовательности частичных сумм при ; , то говорят, что ряд сходится, а число называют суммой ряда. Определение. Если последовательность не имеет конечного предела, то говорят, что ряд расходится.
Геометрический ряд. Рассмотрим ряд, составленный из членов геометрической прогрессии с первым членом и знаменателем Такой ряд называют геометрическим. Предел последовательности частичных сумм этого ряда имеет вид:
Пусть Тогда при и тогда геометрический ряд сходится. Если , то при следовательно, последовательность не имеет конечного предела, то есть геометрический ряд расходится. и,
В рассмотренном нами примере ряд геометрический, поэтому данный ряд сходится и как уже показано Т. е. сумма ряда равна
2. Необходимый признак сходимости ряда. Если ряд сходится, то его общий член стремится к нулю, т. е. Это условие необходимо, но не достаточно для сходимости ряда. Рассмотри следующий ряд: Этот ряд называется гармоническим. Несмотря на то, что предел его n- го члена равен нулю, данный ряд расходится.
Если общий член ряда условию удовлетворяет , то ряд расходится. Пример: Рассмотрим сл. ряд . Последовательность частичных сумм этого ряда не имеет предела. Т. е. данный ряд , т. е. . Т. е. данный ряд расходится.
Пример. Найти сумму следующего ряда: Найти предел
Ответ: 3. Основные свойства сходящихся рядов Свойство 1. На сходимость ряда не влияет отбрасывание, добавление или изменение конечного числа его членов. Свойство 2. Пусть даны два сходящихся ряда. Тогда ряд сходится и .
Свойство 3. Пусть даны сходящийся ряд постоянная С. Тогда ряд сходится и и
3. Ряды Дирихле. Рассмотрим числовой ряд вида: P = const. Гармонический ряд можно рассматривать как частный случай ряда Дирихле при При расходится. . ряд сходится, а при ряд
Признаки сходимости положительных рядов Ряд , в котором все , называется положительным или ряд с положительными членами. Общий признак сходимости рядов. Для того, чтобы положительный ряд , сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.
Признаки сравнения положительных рядов. Пусть даны два положительных ряда и , тогда при всех n, то их сходимости ряда 1) если следует сходимость ряда расходимости . А из следует расходимость ряда.
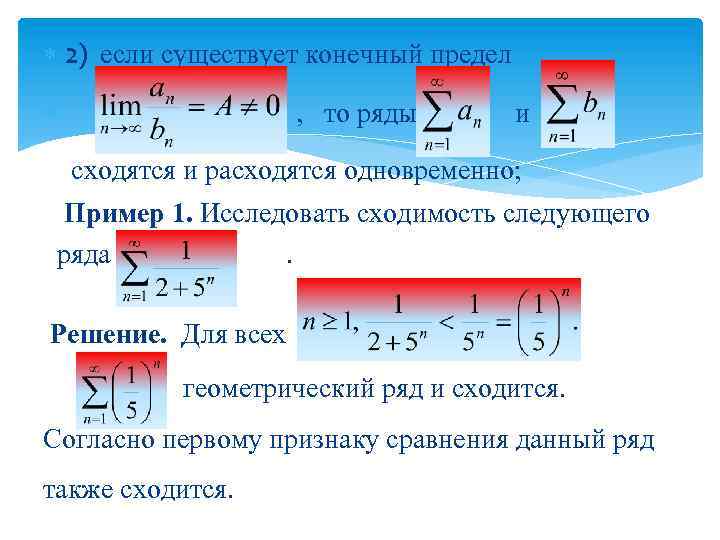2) если существует конечный предел , то ряды и сходятся и расходятся одновременно; Пример 1. Исследовать сходимость следующего ряда. Решение. Для всех геометрический ряд и сходится. Согласно первому признаку сравнения данный ряд также сходится.