l a res it tu ig a D n ig S ! …
Digital Signatures What is a digital signature? A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A digital signature can be used with any kind of message, whether it is encrypted or not, simply so that the receiver can be sure of the sender's identity and that the message arrived intact.
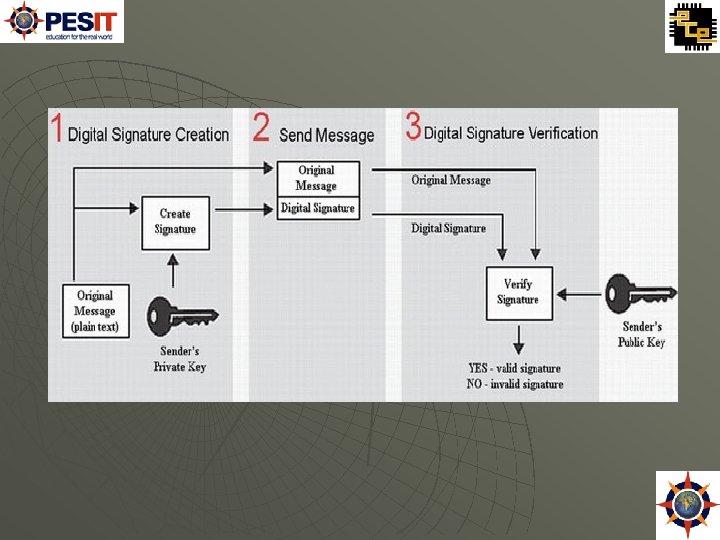
Creation of Digital Signatures A digital signature scheme typically consists of three algorithms: HASHING algorithm. Signature Generation Algorithm A signature verifying algorithm that, given a message, public key and a signature, either accepts or rejects the message's claim to authenticity.
Methods of Encryption based on Privacy Encryption scrambles or modifies a message or document so it cannot be read and understood, except by the intended recipient. A key is necessary to reverse the scrambling or modification, to make the message readable. Methods of Encryption based on Privacy are as follows: • a message may be digitally signed, but not encrypted • a message may be encrypted first, then digitally signed • a message may be digitally signed first, then encrypted
Prerequisites to create a digital signature Public-private digital key pair Certificate Authority. The public key certificate creates proof of the identity of the signer by using the services of a certificate authority. A certificate authority uses a variety of processes to associate the particular public key with an individual. The combination of public key and proof of identity result in a public key certificate - also called a signer's certificate.
Digital Signature Verification It is the process of checking the digital signature by the reference to the original message and a given public key. Verifying also relies on a formula. Here, the formula depends on three inputs: The sequence of characters representing the supposedly originally signed electronic data The public key of the signing party The value representing the supposedly authentic digital signature. The output of the formula is a simple answer: YES or NO.
Digital Signature Schemes The following are the widely used Schemes for Digital Signatures RSA Scheme El. Gamal Scheme Schnorr Scheme Digital Signature Standard (DSS)
RSA Algorithm RSA stands for Rivest, Shamir and Adleman who first publicly described the algorithm RSA involves a public key and a private key. The keys for the RSA algorithm are generated the following way: 1. Choose two distinct prime numbers p and q. 2. Compute n = pq, n is used as a modulus in further steps 3. Compute φ(n) = (p – 1)(q – 1), where φ is Euler's quotient function. 4. Choose an integer e such that 1< e <φ(n) and gcd(e, φ(n)) = 1, i. e. e and φ(n) are co-prime and e is released as the public key exponent. 5. Determine d = e– 1 mod φ(n); i. e. d is the multiplicative inverse of e mod φ(n) and d is kept as the private key exponent.
Digital Signature Standard (DSS) The DSA is used by a signatory to generate a digital signature on data and by a verifier to verify the authenticity of the signature. Each signatory has a public and private key. For both signature generation and verification, the data which is referred to as a message, M, is reduced by means of the Secure Hash Algorithm (SHA) The DSA makes use of the following parameters: 1) 2) 3) 4) p = a prime modulus, where 2 L-1 < p < 2 L for 512 = < L = <1024 and L a multiple of 64 q = a prime divisor of p - 1, where 2159 < q < 2160 g = h(p-1)/q mod p, where h is any integer with 1 < h < p - 1 such that h (p 1)/q mod p > 1 (g has order q mod p) k = a randomly or pseudorandomly generated integer with 0 < k < q The integers p, q, and g can be public and can be common to a group of users. A user's private and public keys are x and y, respectively.
Digital Signature Standard (DSS) The signature of a message M is the pair of numbers r and s computed according to the equations below: r = (gk mod p) mod q and s = (k-1(SHA(M) + xr)) mod q. In the above, k-1 is the multiplicative inverse of k, mod q; i. e. (k-1 k) mod q = 1 and 0< k-1< q. The verification process goes as below: Let M', r' and s' be the received versions of M, r, and s, respectively, and let y be the public key of the signatory. The verifier first checks to see that 0 < r' < q and 0 < s' < q; if either condition is violated the signature shall be rejected. If these two conditions are satisfied, the verifier computes w = (s')-1 mod q ; u 1 = ((SHA(M')w) mod q ; u 2 = ((r')w) mod q ; v = (((g)ul (y)u 2) mod p) mod q. If v = r', then the signature is verified else if v != r’ then the received message could have been modified and hence not authentic
Legal Aspects of Digital Signatures The digital signature is that which makes a document a legal one. It is a representation of assuring that the document meats all legal and is authentic in its framework. The actual digital signature provides the following: • Evidence • Ceremony • Approval • Efficiency
Advantages of Digital Signatures Advantages Authentication, identification of the person that signs. Integrity of data, every change will be detected. Non repudiation, because the author cannot be denied of his work (he created and sent). Imposter prevention Elimination of possibility of committing fraud by an imposter
Disadvantages The disadvantages of using digital signatures involve the primary avenue for any business: money. Though the use of Digital Signatures is very powerful way to secure and authenticate a message or document, its advantages are hampered by lost or theft of keys and the use of vulnerable storage facilities. A number of Digital Signature standard exist which are incompatible with each other and there is a strong need of a standard through which these different methods (keys) can interact.