Л 5 Центр масс Ограниченное в пространстве множество

Л 5 Центр масс Ограниченное (в пространстве) множество материальных точек, произвольно движущихся в пространстве называют механической системой. Рассмотрим такую систему относительно некоторой ИСО K Воображаемую точку с радиус-вектором Z где i - номер точки, n количество точек, mi - масса iой точки и m - масса всей системы точек называют центром масс системы материальных точек Тогда скорость центра масс K rc O Y X 1

Центр масс двух частиц на оси x расположен в точке x. СМ, между частицами ближе к частице большей массы. если x 1=0, х2=d, где d – расстояние между частицами, и m 2=2 m 1, то Обобщая вышеизложенное на систему многих частиц где x – координата i–ой частицы и mi – сумма масс частиц, или mi = M – полная масса системы. Координаты y и z центра масс определяются отношениями: и 2

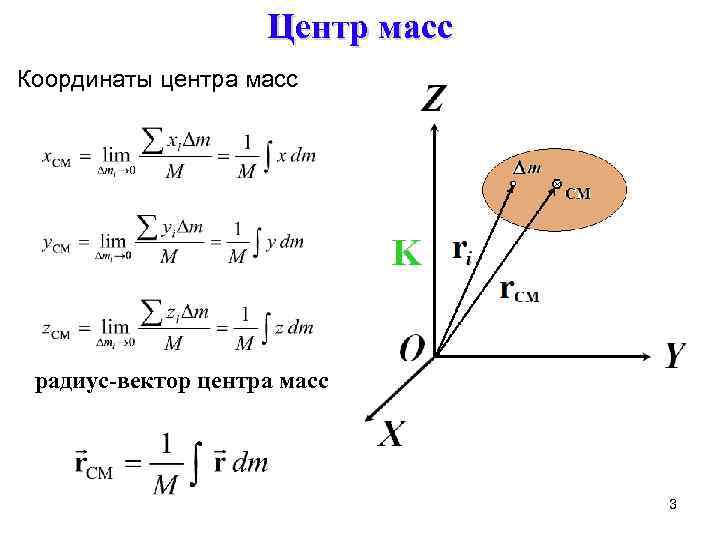Центр масс Координаты центра масс радиус-вектор центра масс 3

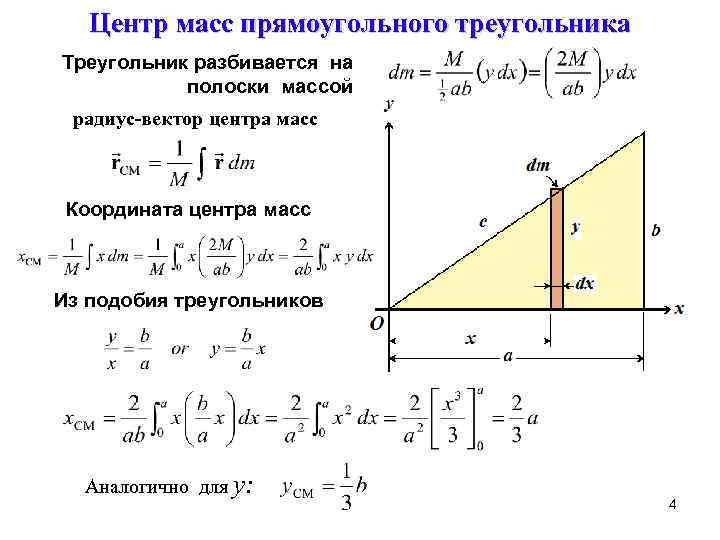Центр масс прямоугольного треугольника Треугольник разбивается на полоски массой радиус-вектор центра масс Координата центра масс Из подобия треугольников Аналогично для y: 4

Центр масс Z является первым динамическим параметром частицы и называется импульсом величину K rc называют импульсом центра масс Таким образом видим, что связь импульса Pc со скоростью vc такая же, как для точки с массой m O Y материальной (масса системы) X Другими словами понятие центра масс представляет строгую математическую процедуру сопоставления произвольной механической системе математически 5 точной модели

Теорема о движении центра масс ускорение центра масс Величина называется вторым динамическим параметром и, согласно 2 закону Ньютона, является силой, действующей на частицу Полученная формула является аналитической формой теоремы о движении центра масс При взаимодействиях каждой из частиц механической системы с окружающей средой, центр масс системы движется таким образом, как будто все силы, действующие на отдельные частицы системы, приложены к одной точке – центру масс 6

Теорема о движении центра масс Силы, действующие на каждую точку системы, разобьем на два типа – силы со стороны всех остальных частиц системы (внутренние силы) – результирующая всех внешних сил В общем виде: F 1 i F 13 F 12 m 3 m 1 (F 1)вш mi По 3 закону Ньютона И теорема о движении центра масс принимает вид: Если система находится во внешнем стационарном и однородном поле, то никакими действиями внутри системы невозможно изменить движение центра масс системы 7

Закон сохранения импульса Механическую систему называют замкнутой, если результирующая всех внешних сил, действующих на систему, равна нулю следовательно ac = 0, т. е. центр масс замкнутой системы относительно произвольной ИСО движется либо равномерно и прямолинейно, либо находится в покое С другой стороны, если система замкнута Итак, получаем закон сохранения импульса Импульс центра масс (т. е. векторная сумма импульсов всех частиц) замкнутой системы сохраняется 8

ДИНАМИКА Описание движения твердого тела 9

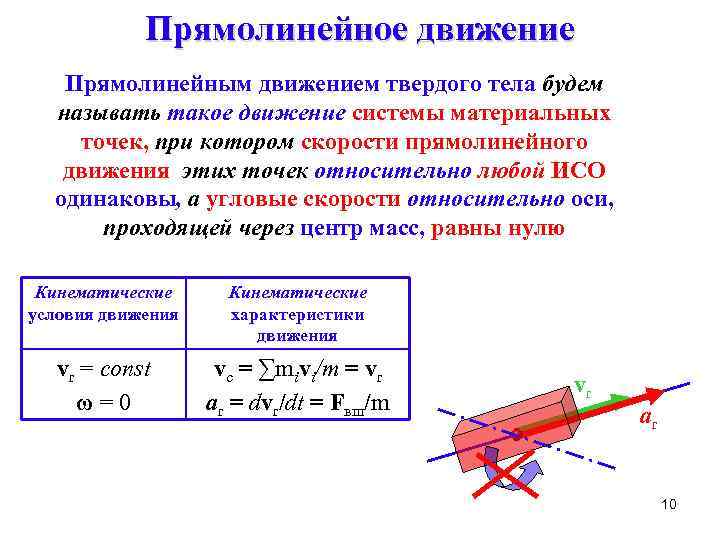Прямолинейное движение Прямолинейным движением твердого тела будем называть такое движение системы материальных точек, при котором скорости прямолинейного движения этих точек относительно любой ИСО одинаковы, а угловые скорости относительно оси, проходящей через центр масс, равны нулю Кинематические условия движения Кинематические характеристики движения vr = const ω=0 vc = ∑mivi/m = vr ar = dvr/dt = Fвш/m vr ar 10

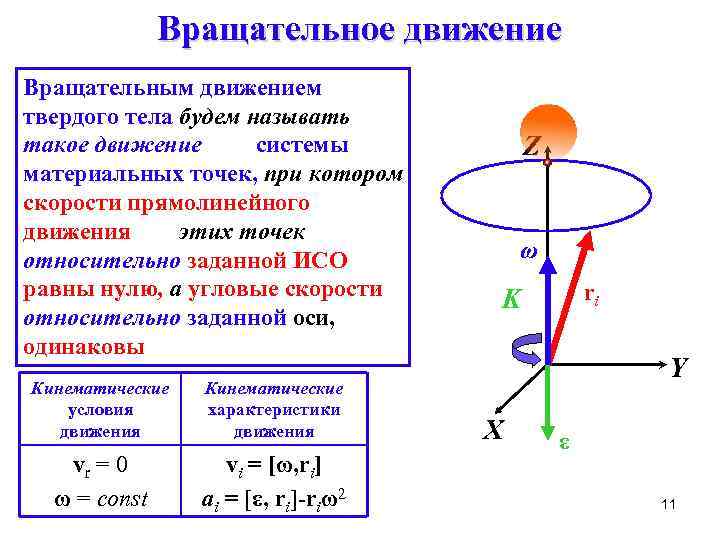Вращательное движение Вращательным движением твердого тела будем называть такое движение системы материальных точек, при котором скорости прямолинейного движения этих точек относительно заданной ИСО равны нулю, а угловые скорости относительно заданной оси, одинаковы Кинематические условия движения Кинематические характеристики движения vr = 0 ω = const vi = [ω, ri] ai = [ε, ri]-riω2 Z ω ri K Y X ε 11

Вращательное движение Для вращательного движения точки введем новые Момент импульса динамические параметры Векторные произведения в этих определениях Момент силы Z Найдем проекции этих выражений на ось ρi вращения (ось Z) ω K θ ri Y 12

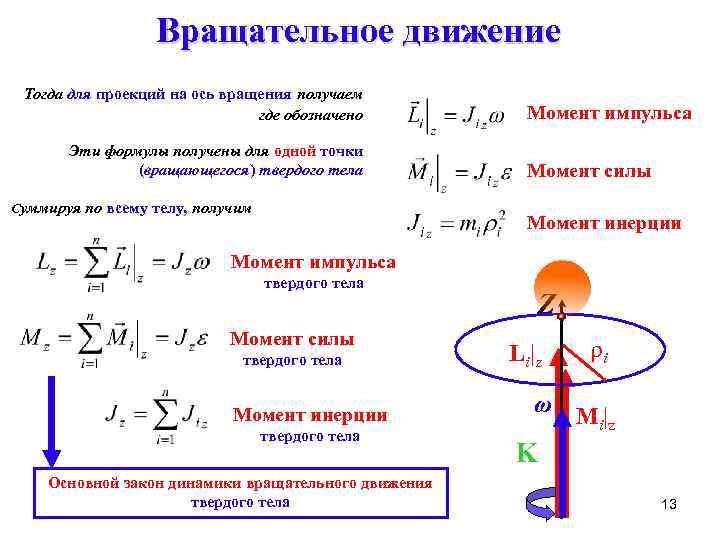Вращательное движение Тогда для проекций на ось вращения получаем где обозначено Эти формулы получены для одной точки (вращающегося) твердого тела Суммируя по всему телу, получим Момент импульса Момент силы Момент инерции Момент импульса твердого тела Момент силы твердого тела Момент инерции твердого тела Основной закон динамики вращательного движения твердого тела Z L i| z ω ρi M i |z K 13

Вращательное движение 14

Основной закон динамики вращательного движения твердого тела Рассмотрим более подробно основной закон динамики вращательного движения твердого тела Найдем производную момента импульса по времени Таким образом получаем основной закон динамики вращательного движения твердого тела в дифференциальной форме Как и прежде, силы, действующие на каждую точку твердого тела, разобьем на внутренние и внешние силы по 3 закону Ньютона 15

Закон сохранения момента импульса Основной закон динамики вращательного движения твердого тела принимает вид Если результирующий момент всех внешних сил, действующих на систему, равен нулю Mвшz = 0, то очевидно Следует отметить, что как и прежде, полученные результаты справедливы только для однородного и стационарного внешнего поля -----------------------------------------------------------------Если результирующий момент всех внешних сил, действующих на механическую систему, совершающую вращательное движение, равен нулю, то систему называют замкнутой по отношению к моментам сил ------------------------------------------------------------------ Никакими действиями внутри замкнутой по отношению к моментам сил системы, находящейся в однородном стационарном поле, невозможно изменить угловую скорость центра масс системы 16

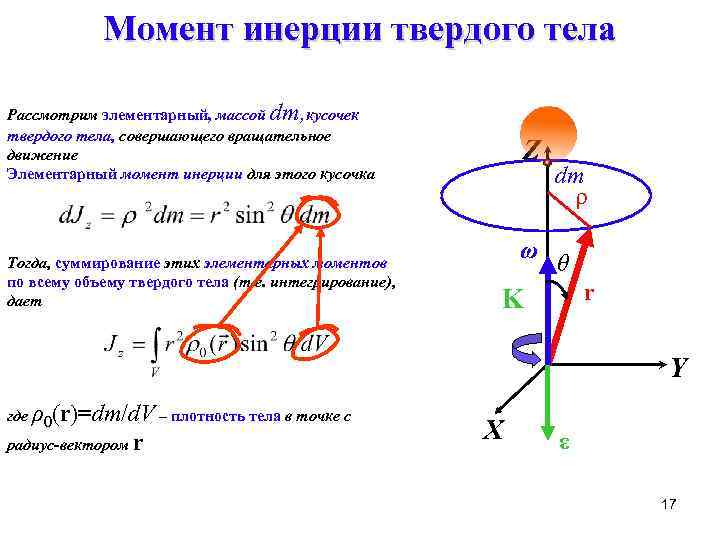Момент инерции твердого тела Рассмотрим элементарный, массой dm, кусочек твердого тела, совершающего вращательное движение Элементарный момент инерции для этого кусочка Тогда, суммирование этих элементарных моментов по всему объему твердого тела (т. е. интегрирование), дает Z ω dm ρ θ r K Y где ρ0(r)=dm/d. V – плотность тела в точке с радиус-вектором r X ε 17

Теорема Штейнера Задача: найти момент инерции Jz произвольного тела массой M относительно некоторой оси Z, если известен момент инерции J 0 этого тела Z' Z центр масс a ρ'i относительно оси Z', проходящей через центр масс тела, параллельно исходной (на расстоянии a) Для решения, выберем произвольную точку тела с массой mi на расстоянии ρi от заданной оси mi ρi M Тогда где ρ'i – расстояние от центра масс тела 18

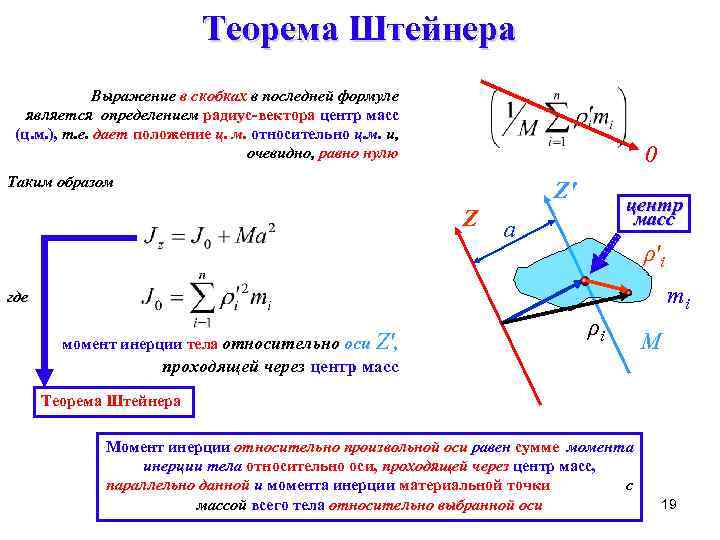Теорема Штейнера Выражение в скобках в последней формуле является определением радиус-вектора центр масс (ц. м. ), т. е. дает положение ц. м. относительно ц. м. и, очевидно, равно нулю 0 Таким образом Z' Z центр масс a ρ'i mi где момент инерции тела относительно оси Z', ρi M проходящей через центр масс Теорема Штейнера Момент инерции относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс, параллельно данной и момента инерции материальной точки с массой всего тела относительно выбранной оси 19