L 32 — Forces and Fields Agenda

L 32 - Forces and Fields. Agenda : 1. Electrical Potential Energy 2. Electrical Potential 3. Gravitational Potential Energy 4. Gravitational Potential 1

1. Electric Potential Energy • Prove that: SI Unit: Joule (J) (Eq. 1) 2

2. Electric Potential • Electric potential VE(r) is UE(r) per unit charge. (Eq. 2) 3

Derivation 1: Potential due to a point charge Q Derive the equation: (Eq. 3) 4

3. Electric potential difference between any two points Potential difference is work done against the electric field to move unit charge from one position to another position. (Eq. 4) 5

4. Consider a constant E field region: e. g. , between the plates of a capacitor. ΔV = - E Δx d. V = - E dx giving the equation: (Eq. 5) • E is the negative of the gradient of V • Thus, the scalar field V can be used to find the vector field E 6

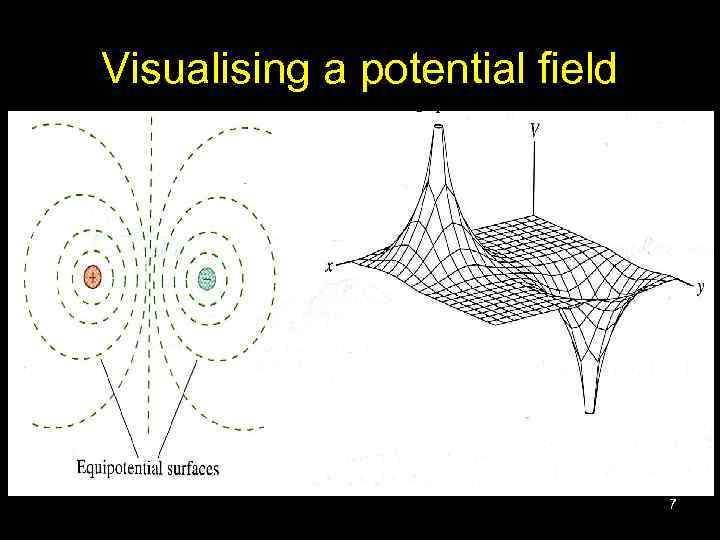Visualising a potential field 7

Example 1: The voltage between the anode and cathode of an electron gun is 2500 V. What is the velocity of the electrons emitted from the gun? 8

Example 2: A parallel plate capacitor consists of two large plates that are 2. 00 cm apart. The potential difference between the plates is 4. 00 V. A) What is the electric field at a distance of 0. 5 cm from the negative plate? B) If a charge of 50. 0 μC is released at a distance 0. 500 cm from the positive plate, what will be its KE when it arrives at the negative plate? 9

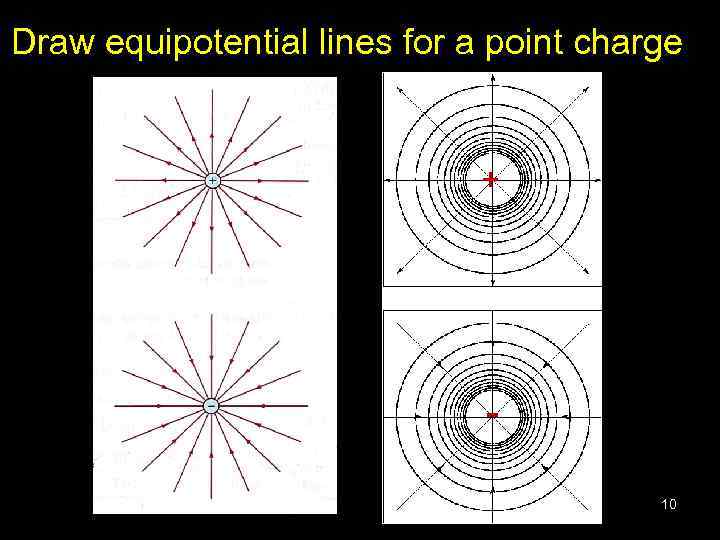Draw equipotential lines for a point charge + 10

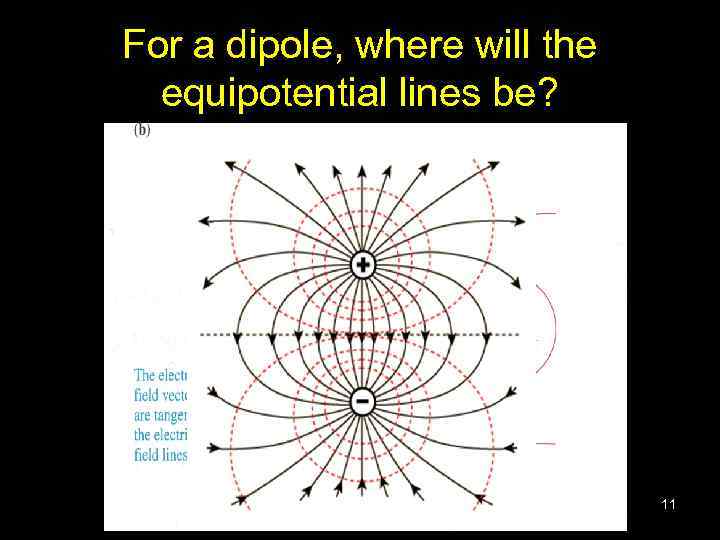For a dipole, where will the equipotential lines be? 11

5. Gravitational Potential Energy (Eq. 6) SI Unit: Joule (J) 12

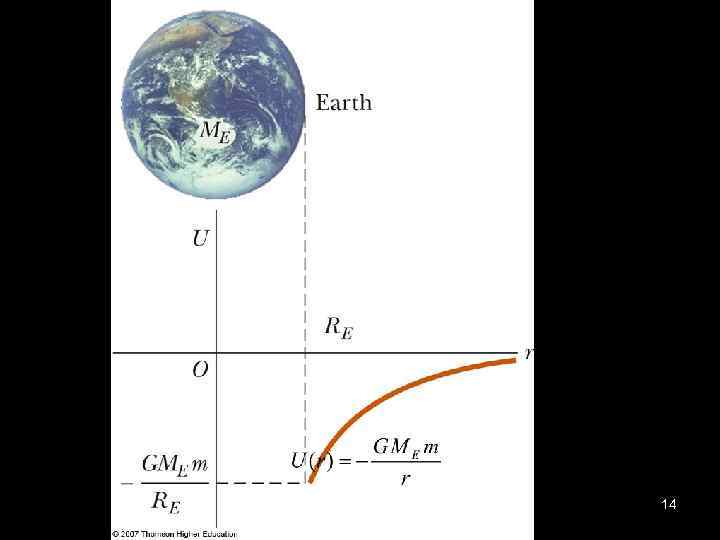
6. The Gravitational field of Earth • Potential energy of mass m near the Earth (Eq. 7) Change of potential energy in moving upwards to height h. (Eq. 8) 13

14

7. Gravitational potential • Gravitational potential VG(x) is the gravitational energy per unit mass. (Eq. 9) SI Unit: Joule per kilogram (J/kg) 15

Derivation 2: Gravitational potential Vg due to sphere of mass M (e. g. , Earth) Recall: Gravitational field is given by Derive (Eq. 10) 16

Example 3 • Calculate the minimum escape velocity of a rocket from the surface of the Earth. 17

Example 4: A 300 kg projectile is launched vertically from the Earth’s surface. a) At what speed must the projectile be launched so that it reaches an altitude equal to the radius of the Earth? b) What is its gravitational potential at this altitude? c) What is its gravitational potential energy? Given ME = 5. 98 x 1024 kg RE = 6. 38 x 106 m G = 6. 67 x 10 -11 N m 2 kg -2 18

Comparison of electrical and gravitational fields 19

Extra Example 5: How much work is required to move a charge of +20. 0 μC from a distance of 3. 00 cm to a distance of 7. 00 cm away from a stationary charge of 30. 0 μC? 20

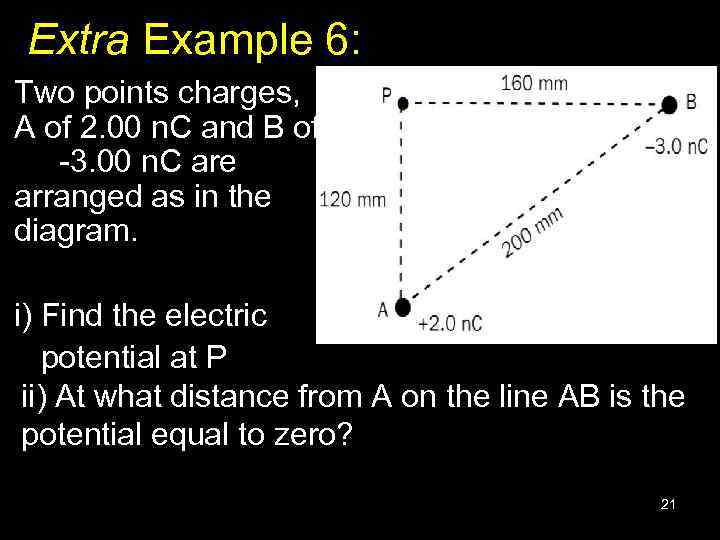Extra Example 6: Two points charges, A of 2. 00 n. C and B of -3. 00 n. C are arranged as in the diagram. i) Find the electric potential at P ii) At what distance from A on the line AB is the potential equal to zero? 21

Further Reading: Serway : 7. 5 - 7. 10 , 15. 1 – 15. 7, 16. 1 – 16. 4; Adams and Allday: 5. 3, 5. 4, 5. 8 - 5. 11, 5. 13. 22

Numerical Answers to Examples 1) V = 2. 96 × 107 m/s 2) a) E = -2. 00 × 102 N/C b) KE = 1. 50 × 10 -4 J 3) 11. 2 km/s 4) a) v = 7. 91 × 103 m/s b) VG = - 3. 13 × 107 J/kg c) UG = - 9. 38 × 109 J 5) W = 1. 03 × 102 J 6) a) V = -18. 7 Volts b) d = 8. 00 cm from A 23

Learning Objectives • Understand, both qualitatively and quantitatively, the relationship between field strength and potential at a point, for electric and gravitational fields • Be able to derive, by integration, the formulae for the potential energy of two particle systems in both electric and gravitational fields • Understand the concepts of potential difference and potential gradient • Know quantitative formulas which define the gravitational potential, electric potential. • Know what an equipotential is • Be able to perform a variety of calculations that demonstrate your understanding 24