L 31 – E & G Forces and Fields. Agenda 1. Forces - The four fundamental forces - Newton’s law and Coulomb’s law 2. Fields : - Electric and gravitational field strength - Field lines - Kepler’s laws - Conservative forces 1
Forces due to gravitation and charge Newton’s law of Gravitation Two particles m 1, m 2 distance r apart Coulomb’s law Two charges q 1, q 2 (in a vacuum) distance r apart G E 2
Constants G is the Universal Gravitational constant G = 6. 67 × 10 -11 ε 0 is the permittivity of free space ε 0 = 8. 85 × 10 -12 k = 8. 99 × 109 Question: What are the units of G, ε 0 and k? 3
Example 1: Suppose the electron and proton inside a hydrogen atom are point masses separated by 5. 29 × 10 -11 m. A) Find the Coulomb force FE and the gravitational force FG between them; B) What is the ratio of these forces? Data: electron charge = 1. 60 × 10 -19 C electron mass = 9. 11 × 10 -31 kg; proton mass = 1. 67 × 10 -27 kg 4
Example 2: A) For an electron orbiting the proton in the hydrogen atom, obtain an equation for the electron’s speed. B) Calculate the speed of the electron at a distance of 0. 530 × 10 -10 m from the Nucleus. C) Should we expect any relativistic effects at this speed? 5
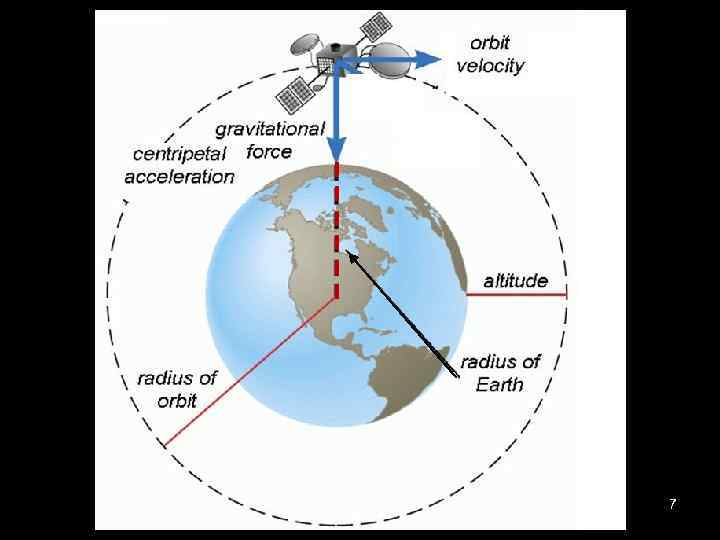
Example 3: A satellite of mass ms is in a circular orbit of radius Rs around the Earth. If the Earth has mass M, show that the speed of the satellite is given by the expression: 6
7
Define “Field” • Field is a region in which a body experiences a force as a result of the presence of some other body. 8
Gravitational Field Electric Field 9
Electric Field due to point charges For fields due to more than one charge, we use the principle of superposition. That is, at any given point in space, we add all E-fields as vectors. 10
Field due to point charges − The flux density and therefore the E field obey inverse square laws; − Field lines start on positive charges and end on negative charges. positive negative − Field lines can never cross. 11
Field lines, flux and flux density • Electric Field lines or “lines of force”. • The tangent to a field line is the direction of the E field at that point. • The flux through an area is the total number of field lines that pass through the area. • The field lines are closer together where the field is greater, i. e. the flux density is greater. • Flux density is the number of lines of force per unit area where the area is perpendicular to the lines. 12
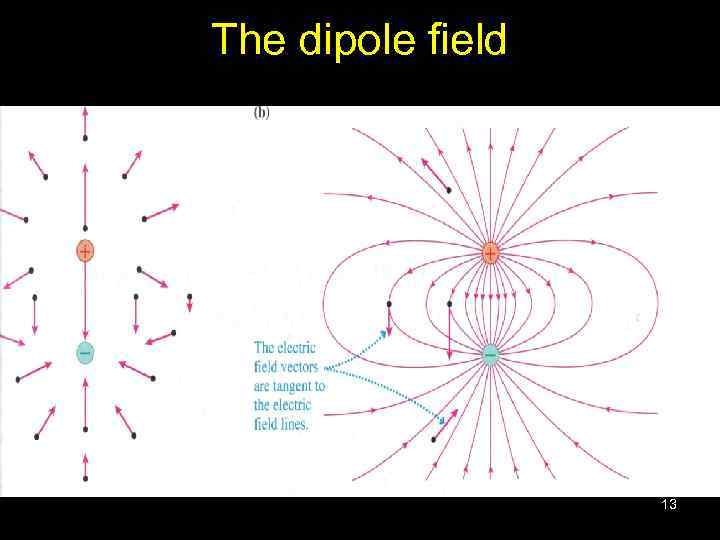The dipole field 13
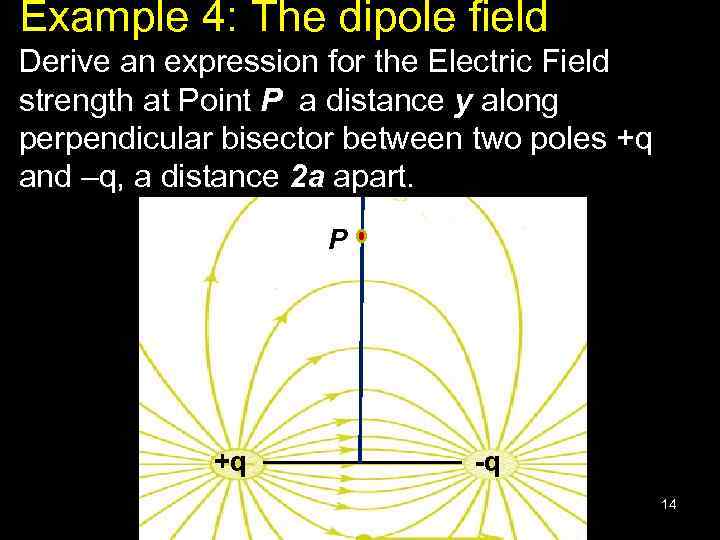Example 4: The dipole field Derive an expression for the Electric Field strength at Point P a distance y along perpendicular bisector between two poles +q and –q, a distance 2 a apart. P +q -q 14
Example 5: Draw the field between two large parallel conducting plates (capacitor). - + + + http: //www. youtube. com/watch? v=DMz 3 Gte. Jf_4 15
Gravitational Field The gravitational field, g, due to a point mass 16
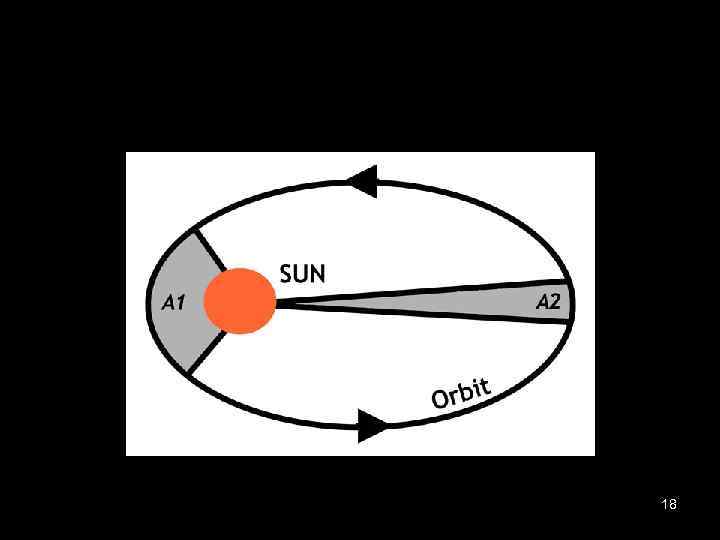
Kepler’s laws 1. The orbit of every planet is an ellipse with the Sun at one of the two foci. 2. A line joining a planet and the Sun sweeps out equal areas during equal intervals of time. 3. The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. (Prove for a circular orbit) 17
18
Example 6: Two points charges, A of 2. 00 n. C and B of -3. 00 n. C, are shown below: i) Find the magnitude and direction of the resultant electric field at P ii) If the charge at B is changed to + 3 n. C, at what distance from A on the line AB is the electric field strength zero?
L 30 - Learning Objectives • State Newton's Law of Universal Gravitation and Coulomb's Law • Know quantitative formulas which define the gravitational field strength, electric field strength. • Understand that field strength is a vector • Be familiar with the ideas of field lines, flux and flux density • Be able to perform a variety of calculations that demonstrate your understanding 20
• Further Reading: • Serway : 7. 5 - 7. 10 , 15. 1 – 15. 7 • Adams and Allday: 5. 1, 5. 2, 5. 7, 5. 9, 5. 14. • Check out: http: //www. physics. sjsu. edu/becker/physics 51/e_ and_v. htm 21
Numerical answers to Examples : • Ex 1) a) FE = 8. 23 × 10 -8 N; b) FE/FG = 2. 27 × 1039; FG = 3. 63 × 10 -47 N. • Ex 2) v = 2. 18 × 106 ms-1 • Ex 6 ) a) E = 1. 64 k. N/C and θ = 49. 8° N of E; b) 89. 9 mm from A. 22