Л 3 Ускорение Производную вектора скорости по времени

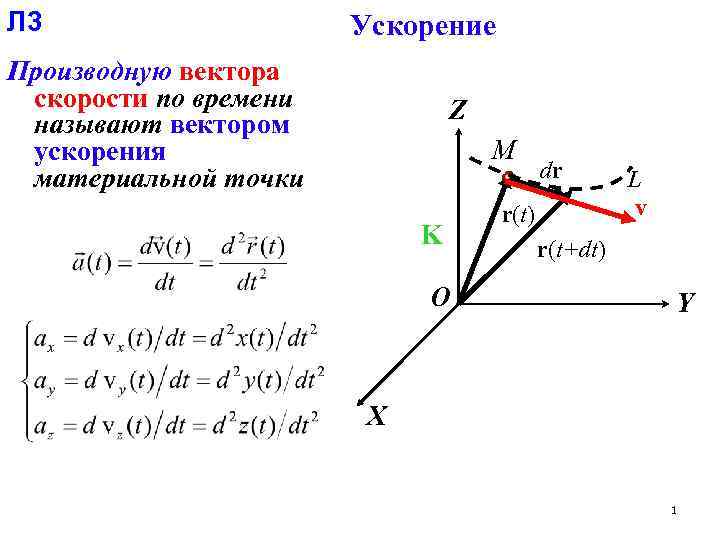Л 3 Ускорение Производную вектора скорости по времени называют вектором ускорения материальной точки Z М K O dr r(t) L v r(t+dt) Y X 1

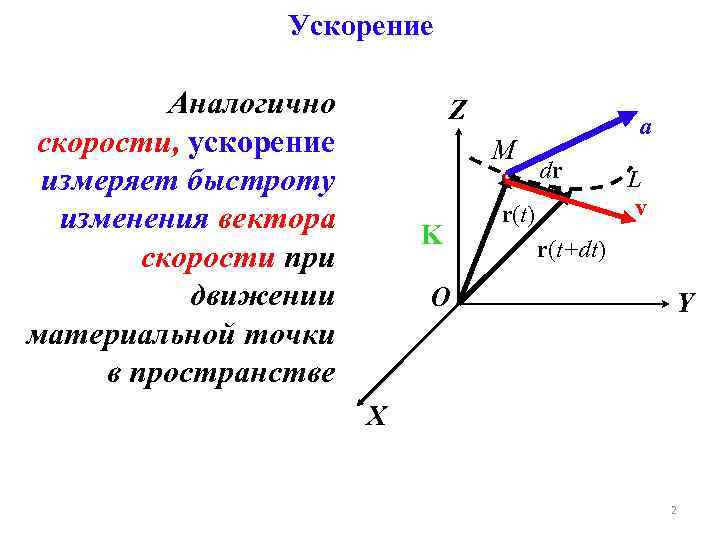Ускорение Аналогично скорости, ускорение измеряет быстроту изменения вектора скорости при движении материальной точки в пространстве Z М K O a dr r(t) L v r(t+dt) Y X 2

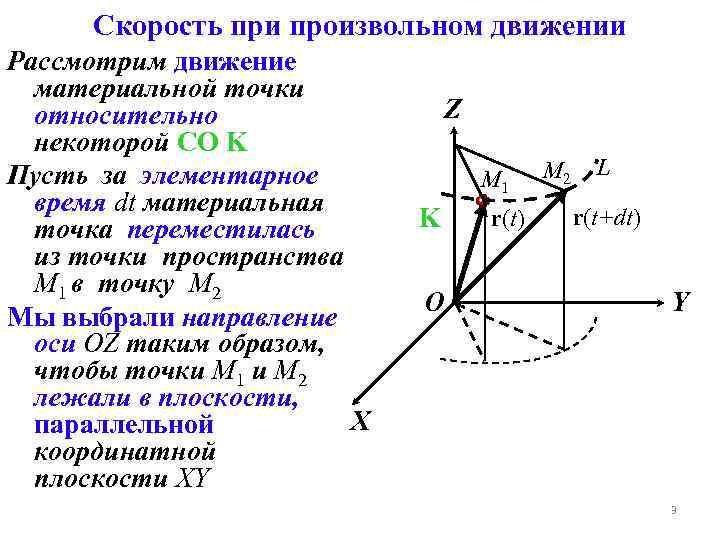Скорость при произвольном движении Рассмотрим движение материальной точки относительно некоторой СО K Пусть за элементарное время dt материальная точка переместилась из точки пространства M 1 в точку M 2 Мы выбрали направление оси OZ таким образом, чтобы точки M 1 и M 2 лежали в плоскости, X параллельной координатной плоскости XY Z М 1 K O r(t) M 2 L r(t+dt) Y 3

Скорость при произвольном движении Z Представим радиус-вектор материальной точки в виде М 1 K L r(t+dt) e(t) где e(t) - единичный вектор, направленный вдоль радиус-вектора Тогда r(t) M 2 O Y X 4

Скорость при произвольном движении Таким образом вектор скорости может быть представлен в виде суммы двух компонент вдоль радиуса-вектора и перпендикулярно радиусу-вектору Z θ de L e(t) K Для того, чтобы найти производную de/dt, проведем единичные векторы вдоль радиус-векторов (первоначального - в момент t и конечного - через промежуток времени dt) Найдем проекции единичных векторов на плоскость XY Очевидно e(t+dt) O e 1 Y e 2 dφ |de| X Тогда длина элементарного отрезка |de| 5

Скорость при произвольном движении производную угла поворота по времени называют угловой скоростью Z ω Следовательно K По определению векторного произведения e 1 de L e(t) θ e(t+dt) dφ Y e 2 |de| X Таким образом, принимая, что вектор угловой скорости направлен вдоль оси вращения получаем 6

Скорость при произвольном движении v компоненту скорости n, перпендикулярную радиус-вектору материальной точки, можем записать теперь в виде Эта скорость является характеристикой вращательного движения материальной точки и называется, соответственно, скоростью вращательного движения Таким образом любое движение материальной точки можно разложить на движения: прямолинейное - вдоль радиус-вектора (со скоростью vr ) и вращательное - относительно начала СО (со скоростью vn ) То есть можно написать 7

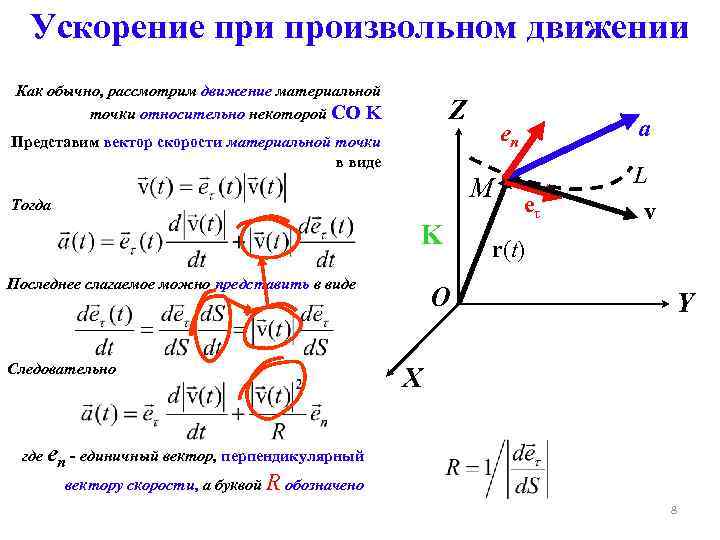Ускорение при произвольном движении Как обычно, рассмотрим движение материальной точки относительно некоторой СО K Z М Тогда K Последнее слагаемое можно представить в виде Следовательно O a en Представим вектор скорости материальной точки в виде eτ L v r(t) Y X где en - единичный вектор, перпендикулярный вектору скорости, а буквой R обозначено 8

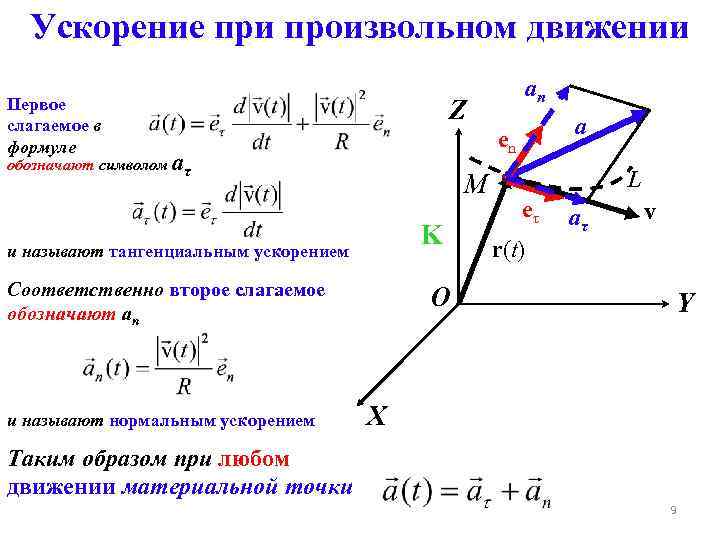Ускорение при произвольном движении Первое слагаемое в формуле Z a en обозначают символом aτ М K и называют тангенциальным ускорением Соответственно второе слагаемое обозначают an и называют нормальным ускорением an O L eτ aτ v r(t) Y X Таким образом при любом движении материальной точки 9

Ускорение при произвольном движении Для того, чтобы выяснить смысл величины R, рассмотрим движение материальной точки по окружности с постоянной по величине скоростью (т. е. ω=const и |r|=const) В этом случае Последнее выражение можно преобразовать по формуле vn (правило BAC-CAB) Получим При движении по окружности a r Следовательно Тогда, вспоминая, что |vn|=|ω||r|, приходим к известному выражению ω Итак видим, что при движении материальной точки по окружности величина R совпадает с радиусом окружности |r| 10

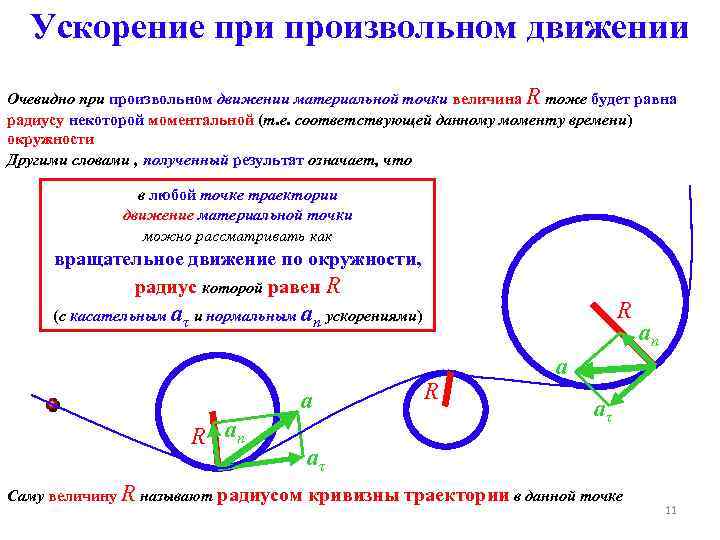Ускорение при произвольном движении Очевидно при произвольном движении материальной точки величина R тоже будет равна радиусу некоторой моментальной (т. е. соответствующей данному моменту времени) окружности Другими словами , полученный результат означает, что в любой точке траектории движение материальной точки можно рассматривать как вращательное движение по окружности, радиус которой равен R R (с касательным aτ и нормальным an ускорениями) a R an Саму величину R называют радиусом R an a aτ aτ кривизны траектории в данной точке 11

Типы ускорений Выясним, какие типы ускорений могут характеризовать движение материальной точки Согласно определению a(t) = dv/dt Тогда, если вспомнить, что при любом движении то несложно найти Напомним, что производную угловой скорости частицы по времени называют угловым ускорением частицы Учитывая, что de/dt=[ω, e], имеем Если теперь раскрыть скобки в последнем векторном произведении, то получим 12

Типы ускорений Величину ar(t) называют ускорением прямолинейного (вдоль радиус-вектора) движения ---------------------------------------- Составляющую ускорения aξ называют переносным ускорением (оно характеризует изменение скорости при движении материальной точки по дуге моментальной окружности) ---------------------------------------- Составляющую ускорения ak называют кориолисовым ускорением (Кориолис) (это ускорение характеризует изменение скорости при движении материальной точки вдоль радиуса вращающейся моментальной окружности) 13

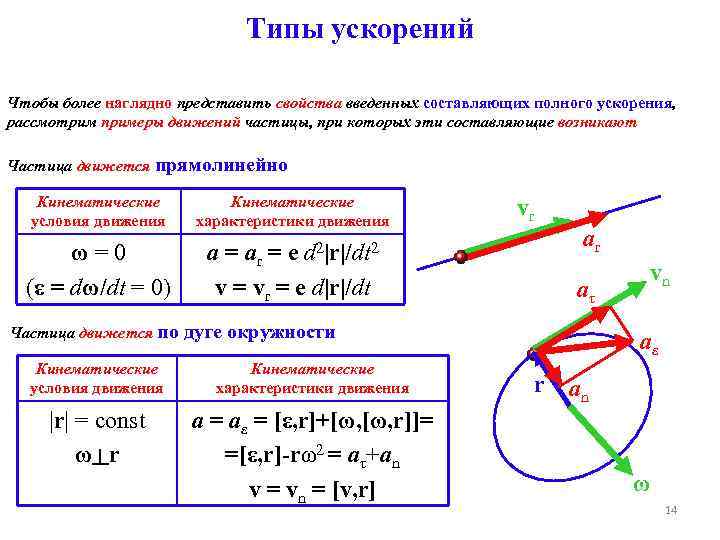Типы ускорений Чтобы более наглядно представить свойства введенных составляющих полного ускорения, рассмотрим примеры движений частицы, при которых эти составляющие возникают Частица движется прямолинейно Кинематические условия движения ω=0 (ε = dω/dt = 0) Частица движется по Кинематические характеристики движения vr d 2|r|/dt 2 a = ar = e v = vr = e d|r|/dt ar aτ дуге окружности Кинематические условия движения Кинематические характеристики движения |r| = const ω ┴r a = aε = [ε, r]+[ω, r]]= =[ε, r]-rω2 = aτ+an v = vn = [v, r] vn aε r an ω 14

Типы ускорений Частица движется по (диска) радиусу вращающегося круга Кинематические условия движения Кинематические характеристики движения ω ω = const vr = const ω ┴r a = 2[ω, vr]+[ω, r]]= =2[ω, vr] - rω2 = ak+an v = vr+[ω, r] = vr+vn an r vr ak Следует обратить внимание на то, что невозможно построить движение при котором ускорение материальной точки сводилось бы только к кориолисову ускорению 15

Восстановление уравнения движения По заданной скорости Пусть задан вектор скорости материальной точки как функция времени Откуда для dr получим Интегрируя это уравнение в пределах от начального момента времени t 0 до любого текущего t, найдем где r(t 0) – радиус-вектор точки в начальный момент времени Таким образом мы видим, что для восстановления уравнения движения по заданной скорости необходимо знать начальное положение материальной точки 16

Восстановление уравнения движения По заданному ускорению Пусть задан вектор ускорения материальной точки как функция времени Тогда для dv получим Интегрируя это уравнение в пределах от начального момента времени t 0 до любого текущего t, найдем где v(t 0) – вектор скорости в начальный момент времени Теперь, для восстановления уравнения движения воспользуемся предыдущим результатом – получим уравнение траектории по заданной скорости Таким образом для восстановления уравнения движения по заданному ускорению необходимо знать два параметра: начальное положение материальной точки и скорость в начальный момент времени 17

Принцип относительности Галилея Во всех инерциальных системах свойства пространства и времени одинаковы, также, и все законы механики Данное утверждение составляет содержание принципа относительности Галилея Формулы преобразования координат при переходе из системы К в систему К’ скорость 18

Преобразования Галилея для однозначного определения кинематических параметров, описывающих движение материальной точки относительно СО K, по измерениям, проведенным в СО K', необходимо знать связь моментов времени t и t’ В классической механике проблема взаимосвязи моментов времени в различных СО решается постулатом Галилея Моменты времени в различных СО совпадают с точностью до постоянной Обычно считают часы синхронизированными так, что const = 0, так что t = t’ несложно получить связь ускорений в произвольных СО, где ao ускорение системы K 0 относительно системы K Эти уравнения называют преобразованиями Галилея 19

Преобразования Галилея Среди всех возможных СО особое место занимает множество таких СО, которые относительно друга движутся с постоянными скоростями (т. е. их относительные ускорения = 0 ) Такие СО называют инерциальными системами отсчета (ИСО) преобразования Галилея для ИСО Последнее уравнение в преобразованиях Галилея для ИСО означает, что ускорение материальной точки во всех ИСО одинаково 20

Галилео Галилей Galileo Galilei 15. 02. 1564 - 08. 01. 1642 Родился в Пизе, Италия (Pisa, Italy) Умер в Арчетри, Италия (Arcetri) астроном, философ и физик важнейшие работы улучшение телескопа разнообразные астрономические наблюдения первый закон движения