L 28 Integration in Physics Setting up

L 28 – Integration in Physics Setting up integrals in physics Geometry of a problem: Areas and Volumes Finding masses Finding moment of inertia 1

2

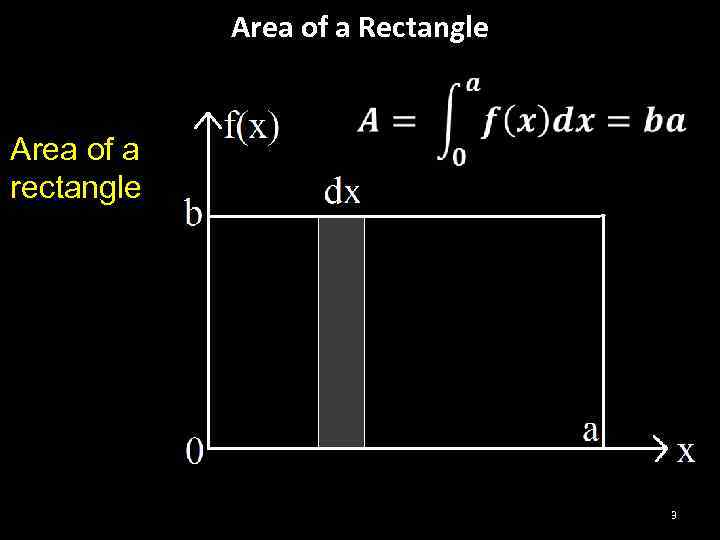Area of a Rectangle Area of a rectangle 3

Area and Volume Elements of Simple Geometric Objects With Central and Axial Symmetry Area of a Circle R r dr 4

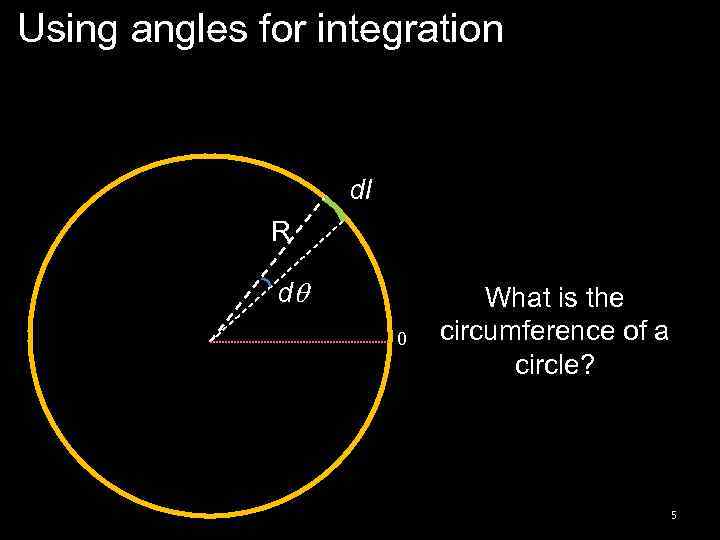Using angles for integration dl R dq 0 What is the circumference of a circle? 5

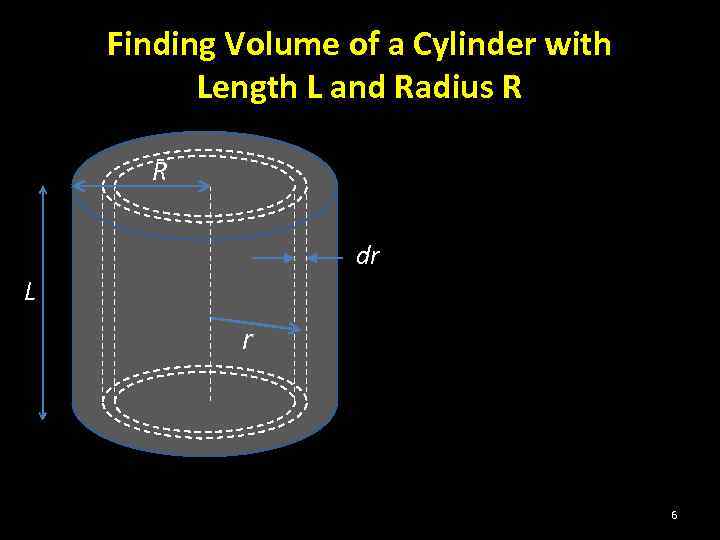Finding Volume of a Cylinder with Length L and Radius R R dr L r 6

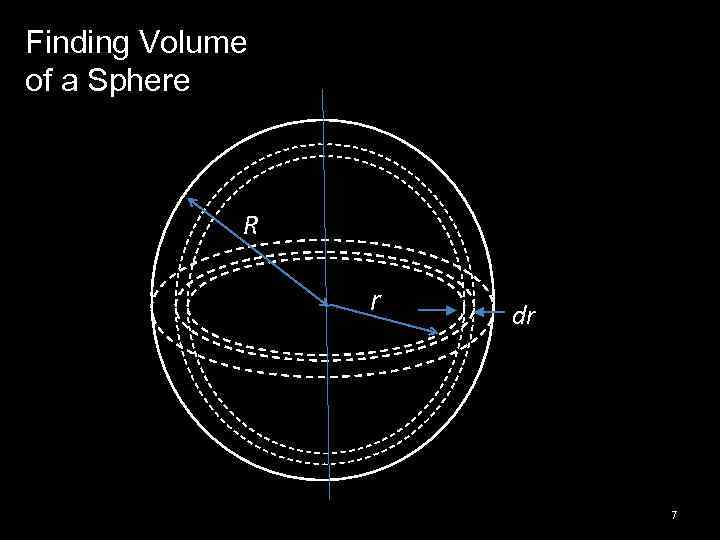Finding Volume of a Sphere R r dr 7

Finding masses Example 1: R The mass density of an axially symmetric solid cylinder L of height L and radius R changes as follows: Find the total mass of the cylinder. 8

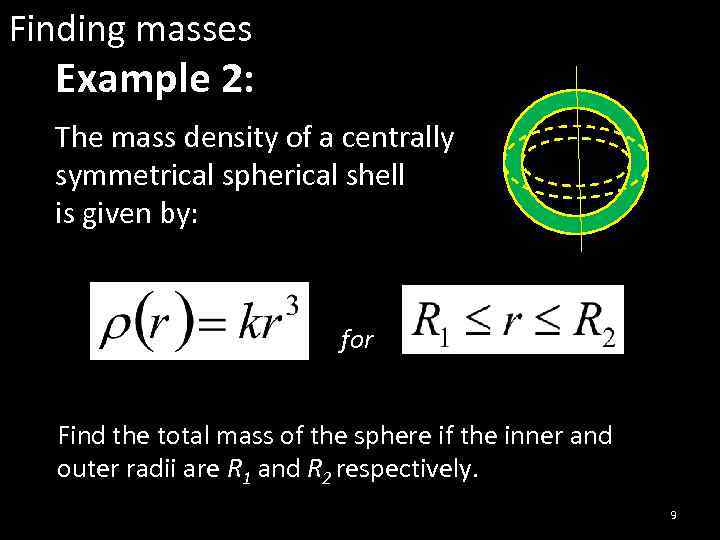Finding masses Example 2: The mass density of a centrally symmetrical spherical shell is given by: for Find the total mass of the sphere if the inner and outer radii are R 1 and R 2 respectively. 9

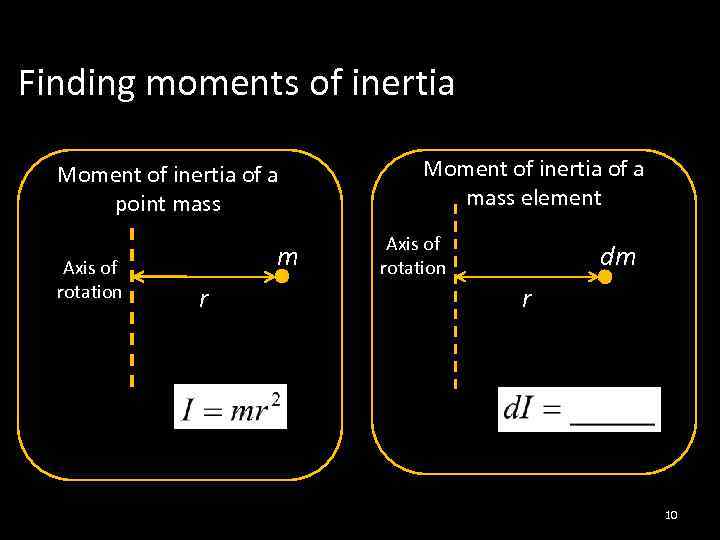Finding moments of inertia Moment of inertia of a point mass Axis of rotation m r Moment of inertia of a mass element Axis of rotation dm r 10

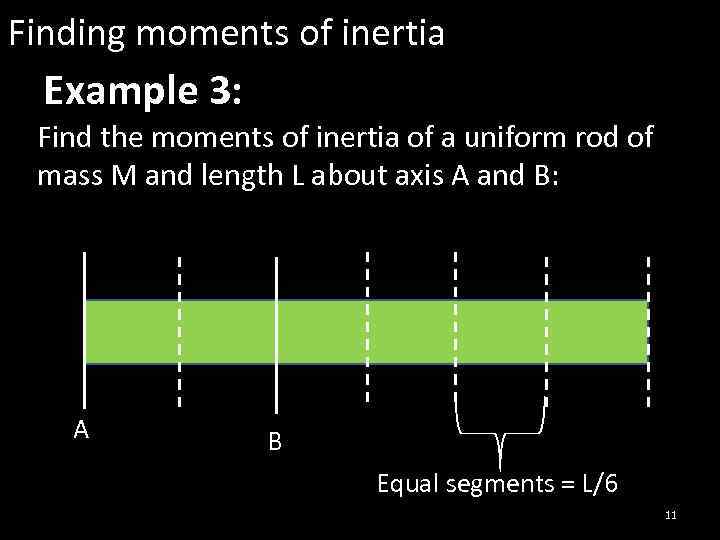Finding moments of inertia Example 3: Find the moments of inertia of a uniform rod of mass M and length L about axis A and B: A B Equal segments = L/6 11

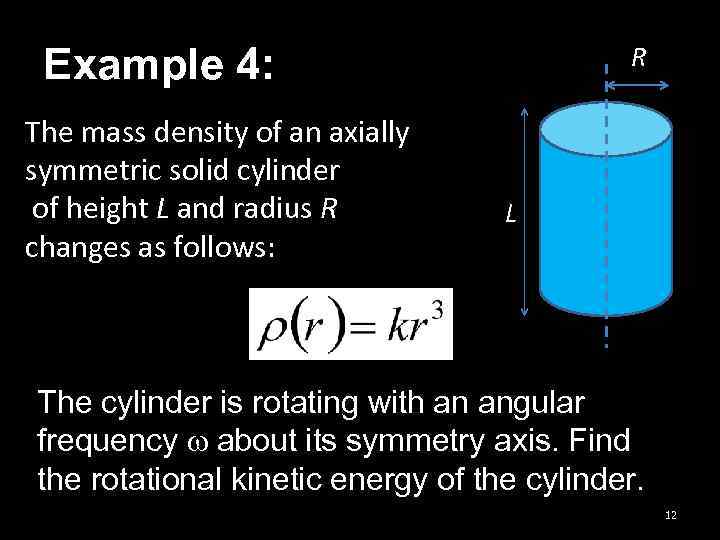Example 4: The mass density of an axially symmetric solid cylinder of height L and radius R changes as follows: R L The cylinder is rotating with an angular frequency w about its symmetry axis. Find the rotational kinetic energy of the cylinder. 12

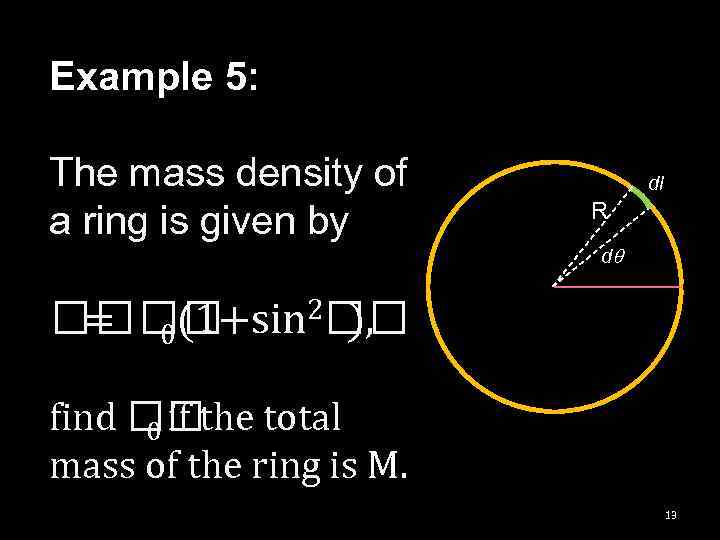Example 5: The mass density of a ring is given by dl R dq 0 2 0(1+sin ), = find the total 0 if mass of the ring is M. 13

By the end of this lecture you should be able to: • Know the Importance of Integration in Understanding Physics • Find the Area of simple Geometric Shapes using integration • Find the Total Mass and Center of Mass (centroid) of simple Geometric Shapes • Set up Formulas for other physical examples of changing characteristics ( mass density, charge density, kinetic energy, etc…) and • Use these formulas in integrals to solve for the unknowns 14

Additional Resources • http: //www. intmath. com/applicationsintegration/1 -apps-indefinite-integral. php • http: //hyperphysics. phyastr. gsu. edu/hbase/hframe. html A general site that can help you find specific example from many different areas of physics 15

Additional Slides 16

Integration Variable and Integrand §Generic expression for an integral (one dimensional) f(x) is the integrand, x is the integration variable, “a” and “b” are the limits of integration 17

Integration Variable and Limits of Integration §In many cases, integration variables are x, y, z coordinates, radius, length, height, volume etc. §In other words, mathematical/geometrical values usually serve as integration variables §Try to reduce the integration variable to the simplest possible case, for example volume to a function of radius, area to length times width etc §Limits of integration are usually defined in the problem (explicitly or implicitly) §Wrong limits of integration will definitely lead to a wrong solution 18

The Integrand §Integrands are crucial for integration and represent the essence of the physical problem in hand §Integrands are usually physical quantities such as density, mass, charge, moment of inertia, field strength etc times some mathematical values. §Once you have defined the integrand properly, the problem is mostly done §Even though you might write initially the differential of a physical quantity, dm for example, you then reduce it to the differential of mathematical/geometrical variable (dm= d. V) 19

Splitting the Problem § Integration means you have to sum the small parts of the problem together § In order to do this, you have to split the problem in hand into smaller problems § The smaller problems must satisfy the following three conditions: 1. Simplify the original problem. Usually this means the integrand can be treated as a constant in a smaller problem. 2. Reproduce the original problem when summed together 3. The relative error must go to zero when the scale of the problems decreases. 20

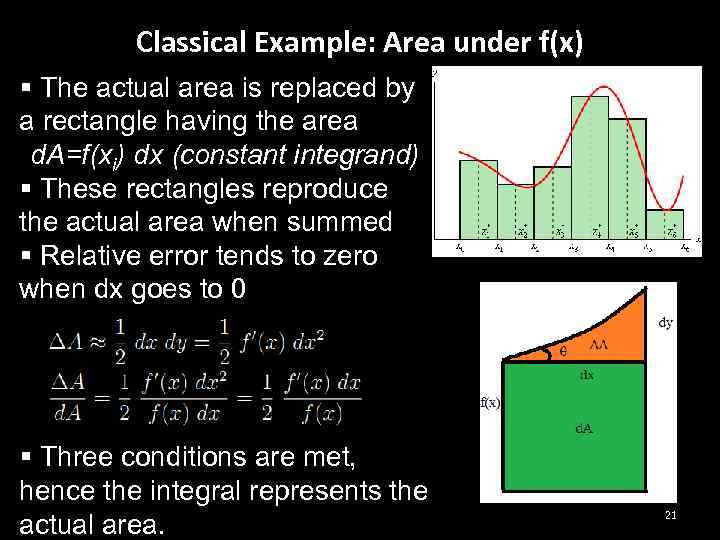Classical Example: Area under f(x) § The actual area is replaced by a rectangle having the area d. A=f(xi) dx (constant integrand) § These rectangles reproduce the actual area when summed § Relative error tends to zero when dx goes to 0 § Three conditions are met, hence the integral represents the actual area. 21

Typical Errors § The smaller problems are not simpler than the original problem. In this case you will not be able to solve the original problem. § The smaller problems do not reproduce the original problem. In this case you will obtain a solution for some other problem. § Relative error does not go to zero when the scale of the problems is reduced. In this case you will end up with a wrong solution. Where is the mistake here? 22

Physical Example: Mass of a Solid Sphere § Density is given as = 10. 0 – 2. 00 r 2 [kg m-3]. §Radius of the sphere is 1. 00 meter §You have volume, radius and density §Following our observations, mathematical values such as volume or radius will be the integration variable §Similarly, the only physical value, density, must be in the integrand §Limits of integration are given explicitly (R=1. 00 m), and implicitly (solid sphere, hence starts at zero). 23

Physical Example: Mass of a Solid Sphere ctd §In order to find the total mass, you have to split it into small masses dm= d. V § There are different ways you can split the sphere, for example into disks or into spherical shells. You have to choose the one that leads to constant integrand. §The splitting into disks will not simplify the problem, since the disks will be of varying density 24

Physical Examples: Mass of a Solid Sphere ctd The splitting into spherical shells will do the job, because: • For a spherical shell, the radius is constant, so is the integrand; • The addition of spherical shells forms a solid sphere; • The relative error tends to zero as dr goes to zero (prove it). 25

Physical Examples: Mass of a Solid Sphere ctd § Collecting all results together, we obtain the following integral for the mass §The integrand here is (constant for the same r) §The integration variable is the radius r §At this point, the integral is set and the only thing left to do is the integration (evaluate the integral using = 10. 0 – 2. 00 r 2 [kg m-3] and R=1. 00 m). 26

Physical Example: Moment of Inertia §The geometry of smaller problems depends on the problem in hand §For example, find the moment of inertia for a solid sphere of constant density § In this case, the split into disks would be beneficial §You can use the moment of inertia for a solid disk I=1/2 MR 2 §The radius of a disk depends on z as §The mass of the disk is §The moment of inertia is then (calculate it) 27

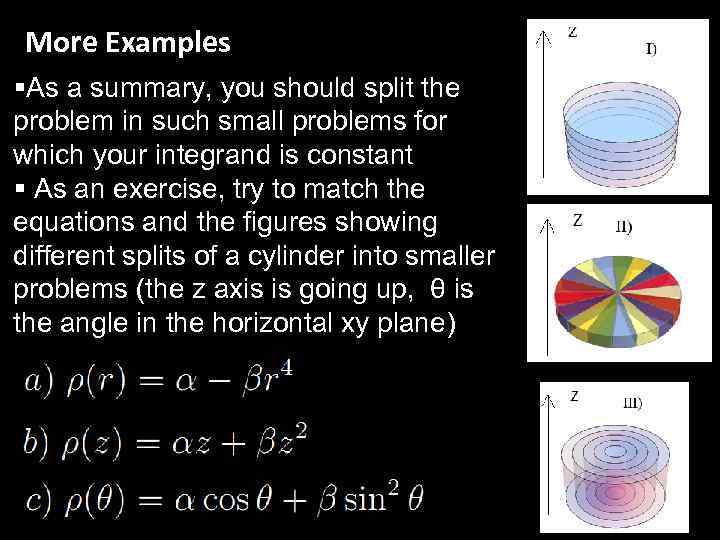More Examples §As a summary, you should split the problem in such small problems for which your integrand is constant § As an exercise, try to match the equations and the figures showing different splits of a cylinder into smaller problems (the z axis is going up, θ is the angle in the horizontal xy plane) 28