L 24 — Atomic Physics Quantum Physics 2 Outline

L 24 - Atomic Physics/Quantum Physics 2 Outline: 1. 1 - Rutherford's experiment; 1. 3 - The neutron; 1. 4 - Representation of the nucleus; 2. 1 - Emission and absorption spectra, spectroscopy; 3. 0 - The Bohr model; 3. 1 - Energy levels and transitions; 3. 2 - Bohr's electron orbits; 4. 0 -The wave function, probability density, wave-particle duality; 4. 2 - Schrodinger's atom; 1

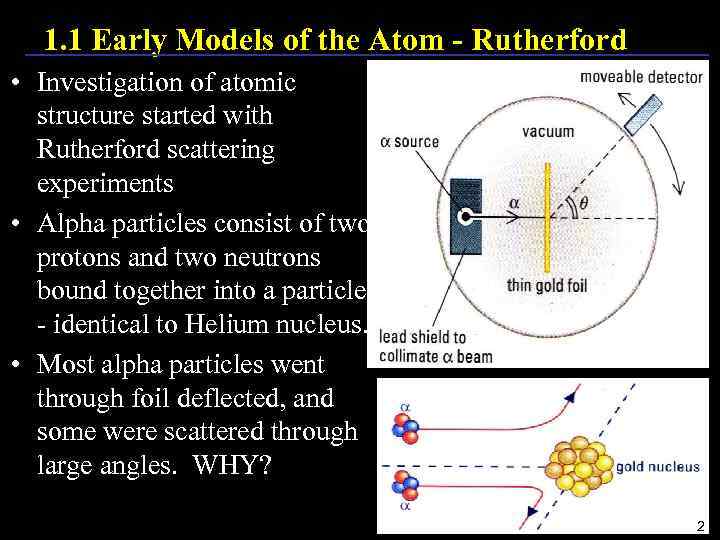1. 1 Early Models of the Atom - Rutherford • Investigation of atomic structure started with Rutherford scattering experiments • Alpha particles consist of two protons and two neutrons bound together into a particle - identical to Helium nucleus. • Most alpha particles went through foil deflected, and some were scattered through large angles. WHY? 2

1. 2 Rutherford’s Model (cont. ) Conclusions from Rutherford’s experiment • Planetary model (most of atom is empty) • Positive charge located at the centre of atom (nucleus) • Electrons orbit the nucleus (like planets around stars) 3

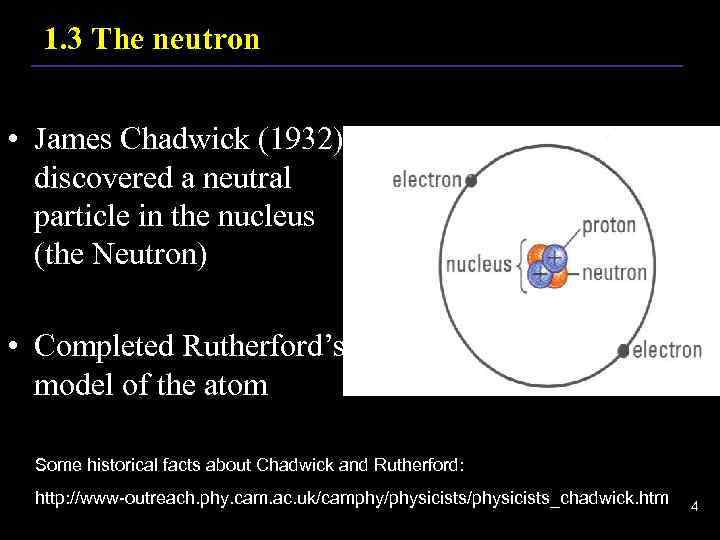1. 3 The neutron • James Chadwick (1932) discovered a neutral particle in the nucleus (the Neutron) • Completed Rutherford’s model of the atom Some historical facts about Chadwick and Rutherford: http: //www-outreach. phy. cam. ac. uk/camphy/physicists_chadwick. htm 4

1. 4 Representation of the nucleus • One writes the structure of the nucleus of an atom X as follows: • A (Mass number) = number of protons and neutrons • Z (Atomic number) = number of protons Example : 4 Has 2 protons, 2 neutrons 2 He and is called “Helium 4” 5

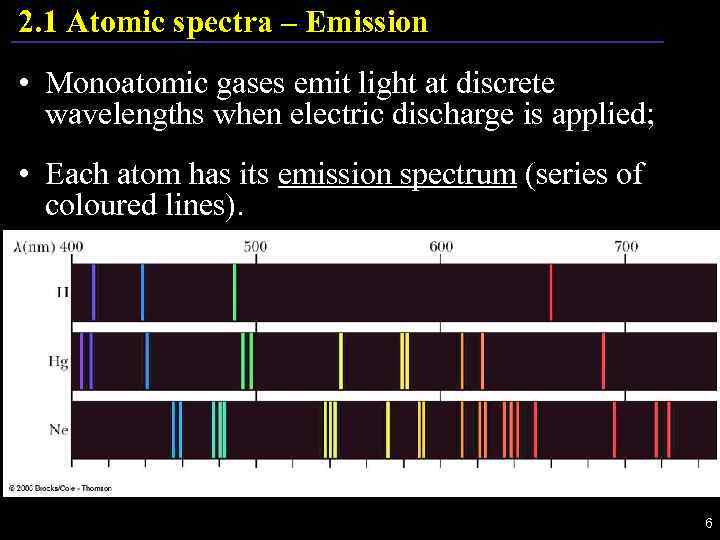2. 1 Atomic spectra – Emission • Monoatomic gases emit light at discrete wavelengths when electric discharge is applied; • Each atom has its emission spectrum (series of coloured lines). 6

2. 2 Atomic spectra – Absorption • Individual atoms can also absorb light at specific wavelengths; • The absorbed wavelengths of an atom form its absorption spectrum (series of dark lines); • Example: spectrum of absorption of white light by a hydrogen gas. 7

2. 3 Atomic spectroscopy • Atomic spectral lines (specific wavelengths) observed in emission and absorption spectra • Each atom has a given set of spectral lines • Spectroscopy studies allow determination of elemental composition of a source or a sample (e. g. detection of atomic elements in planets’ and stars’ atmospheres) 8

3. The Bohr Model of the Atom (3 Postulates) Postulate 1 Only certain electron orbits are stable and allowed where each orbit has a specific energy level; The greater the radius, the higher the energy level; In these orbits no energy in the form of EM radiation is emitted, so the total energy of the atom remains constant. 9

3. The Bohr Model of the Atom (3 Postulates) Postulate 2 Radiation is emitted by the hydrogen atom when the electron “jumps” from a more energetic initial state to a less energetic state. The frequency of the radiation emitted in the jump is related to the change in the atom’s energy, given by where Ei > Ef 10

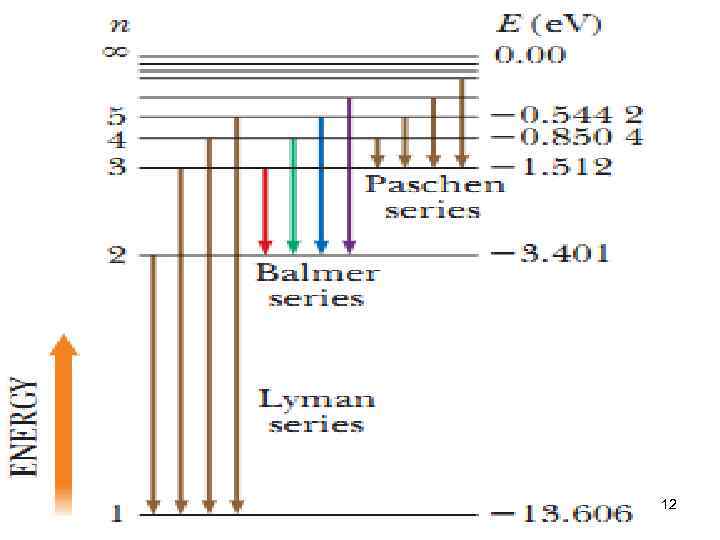
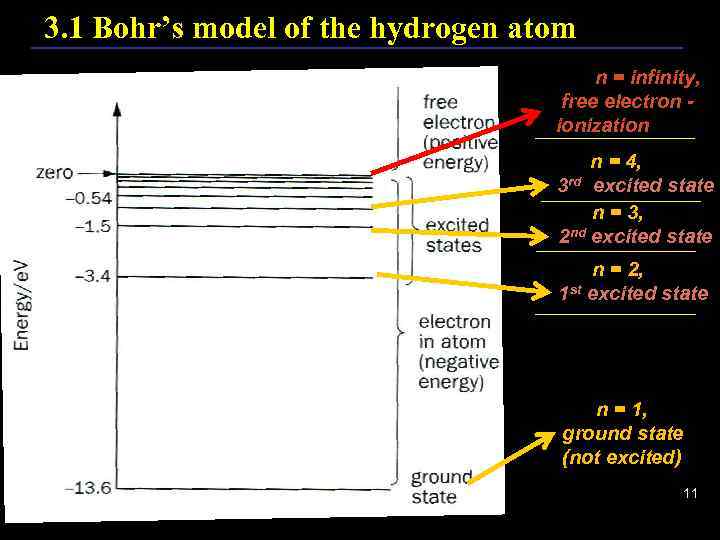3. 1 Bohr’s model of the hydrogen atom n = infinity, free electron ionization n = 4, 3 rd excited state n = 3, 2 nd excited state n = 2, 1 st excited state n = 1, ground state (not excited) 11

12

3. 2 Hydrogen quantized energy levels • In a hydrogen atom, when an electron moves from the first excited state (n=2) to the ground state (n=1), a photon of energy: hf = -3. 4 - (- 13. 6) e. V= 10. 2 e. V is emitted For the hydrogen atom, the energy levels are given by: (eq. 1) 13

3. 2 Hydrogen quantized energy levels (cont. ) In general, for a transition from an energy state m to an energy state n (m n) we write: (eq. 2) if m > n ! Substituting Eq. 1 into Eq. 2 : (eq. 3) 14

3. 3 The Bohr Model of the Atom (continued) Postulate 3 The circumference of an electron’s orbit must contain an integral number of de Broglie wavelengths: Electrons’ orbits in Bohr’s atomic model are similar to standing waves fitting into the circumferences of the electrons’ orbits: 15

3. 3 Bohr’s electron orbits (cont. ) • The requirement of standing waves along the circumference of stable orbits yields: • the quantization of the electron’s angular momentum requires/defines the principal quantum number n; • Other quantum numbers have been introduced to explain other experimental observations and properties, e. g. orbital quantum number ℓ 16

Example 1: Bohr’s atomic model a) An electron from a Hydrogen atom moves from the 3 rd excited state to the 1 st excited state. Is this transition followed by a photon emission or absorption? b) What is the wavelength of this photon? c) What is the minimum frequency of a photon that ionizes a hydrogen atom in its n = 4 state? d) What happens to the excess energy of a photon if it has a frequency greater than the minimum frequency required for ionization? 17

4. The Wave Function ψ • The wave nature of matter, e. g. electron, can be described by a probability wave function, ψ ; • ψ(x, t) depends on position and time, and can be used to determine the probability of locating the electron; • Schrödinger’s wave equation describes matter waves, such as electron waves, and the behaviour of atomic and nuclear systems. It is used to calculate ψ(x, t); • ψ(x, t) is similar to classical waves, which produce interference patterns. 18

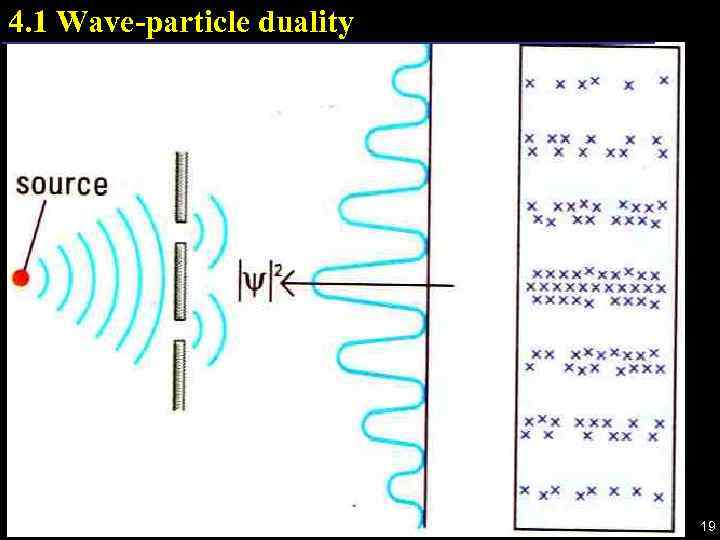4. 1 Wave-particle duality 19

20

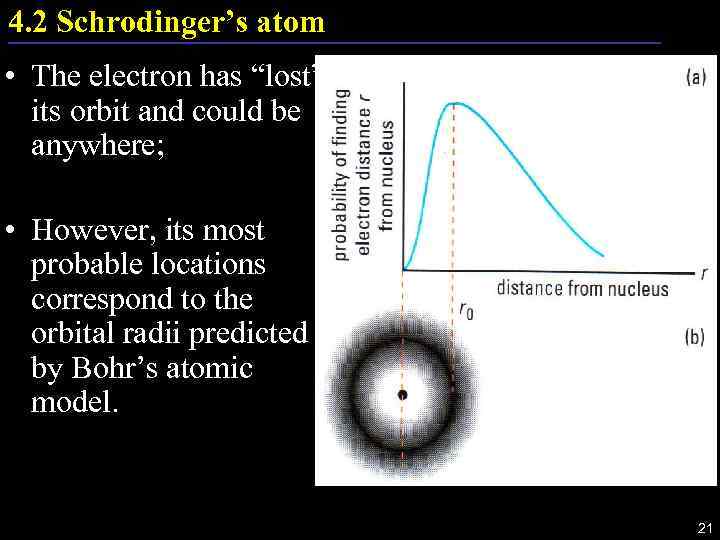4. 2 Schrodinger’s atom • The electron has “lost” its orbit and could be anywhere; • However, its most probable locations correspond to the orbital radii predicted by Bohr’s atomic model. 21

22

Example 2. Schrodinger’s Wave Equation Consider a particle of mass m travelling along the xaxis and interacting with the surroundings through a potential energy function U(x). Then: 23

Checklist Introduction to quantum physics 2 • Know Thomson’s model. Understand why it fails. • Know Rutherfords experiment and understand what conclusions can be derived from it. • Understand how does the neutron fits into Rutherford’s model of an atom. • Know the representation of the nucleus • Understand the origin of emission and absorption spectra spectroscopy. • Understand the Bohr model and the relevant postulates. • Understand the concept of energy levels and transitions between them. • Understand the concept of Bohr's electron orbits and standing waves. • Understand the concept of a wave function, probability density, wave-aprtic duality, Schrodinger's atom. 24

Further Reading: • Serway: Sections 28. 1 – 28. 5 • Adams and Allday: Sections 8. 7, 8. 9 -8. 10 Suggested Resource: Dr. Quantum and the Quantum Double Slit Experiment http: //www. youtube. com/watch? v=Df. Pepr. Q 7 o. Gc Answer to Example 1: a. ) emitted b. ) 487 nm c. ) 2. 05 × 1014 Hz d. ) The excess energy is transferred to the ejected electron as KE. 25