L 15 Introduction to Waves 1 Types of

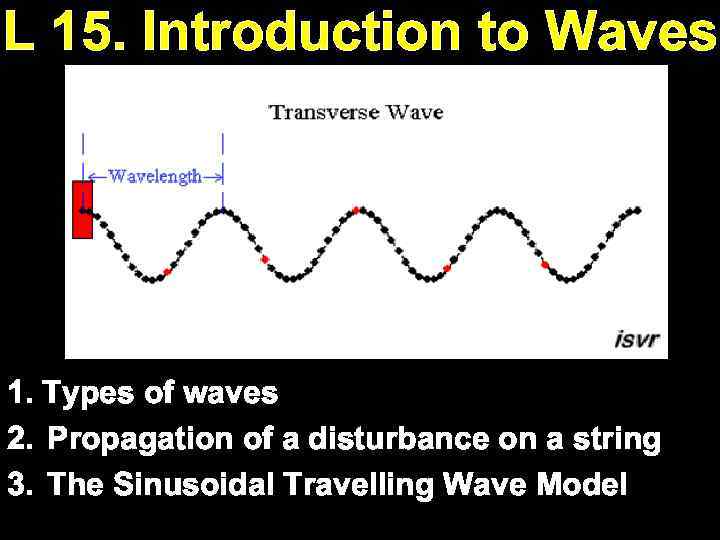L 15. Introduction to Waves 1. Types of waves 2. Propagation of a disturbance on a string 3. The Sinusoidal Travelling Wave Model

Announcements Today, Monday th 24 Nov • Group leaders MUST submit their windmills in the Newton’s lab 4. 00 pm- 5. 00 pm • No extension of deadline

Tomorrow, Tue th 25 Nov • ALL students to be present for final testing at 2. 30 pm, Atrium in front of block 9. • Group leaders should collect windmills at 2. 00 pm from Newton’s lab.

Support sessions • Sign up sheets for support sessions are placed in front of Physics office 2422 ( B ).

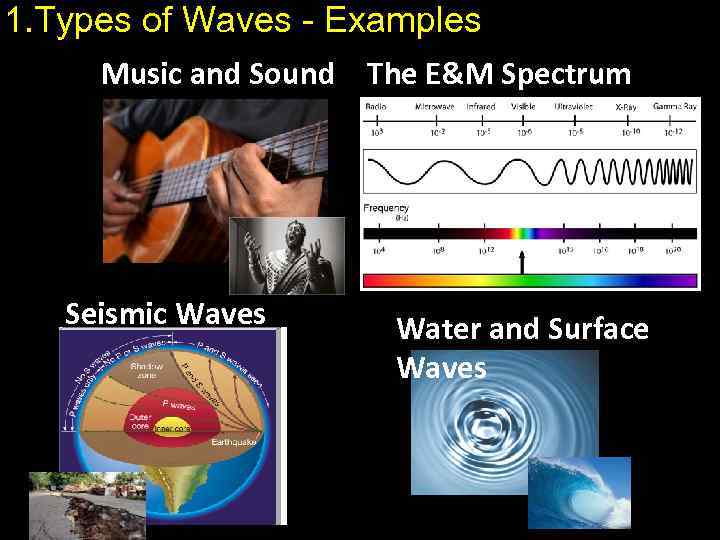1. Types of Waves - Examples Music and Sound The E&M Spectrum Seismic Waves Water and Surface Waves

1. 1 Longitudinal waves In a longitudinal wave, the direction of vibration of each particle is parallel to the wave’s direction of motion. 6

Longitudinal Waves 7

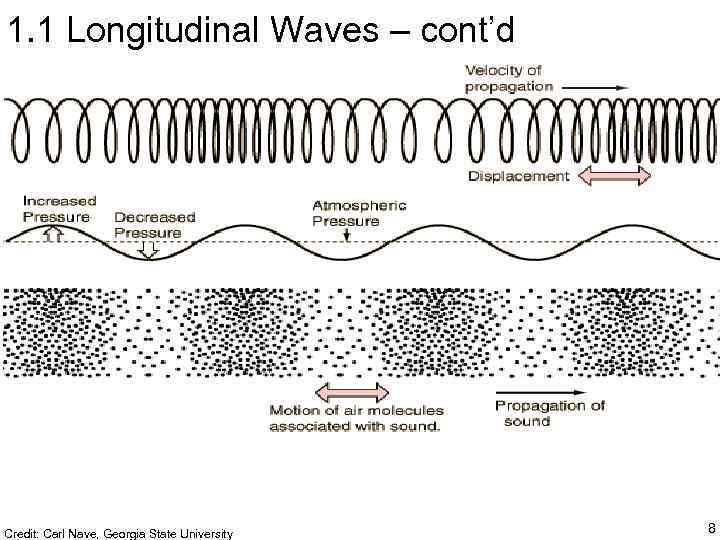1. 1 Longitudinal Waves – cont’d Credit: Carl Nave, Georgia State University 8

1. 1 Longitudinal Waves (Cont’d) The sound wave travels horizontally, as individual particles oscillate back and forth 9 Credit: Dr Dan Russel, Ketting University

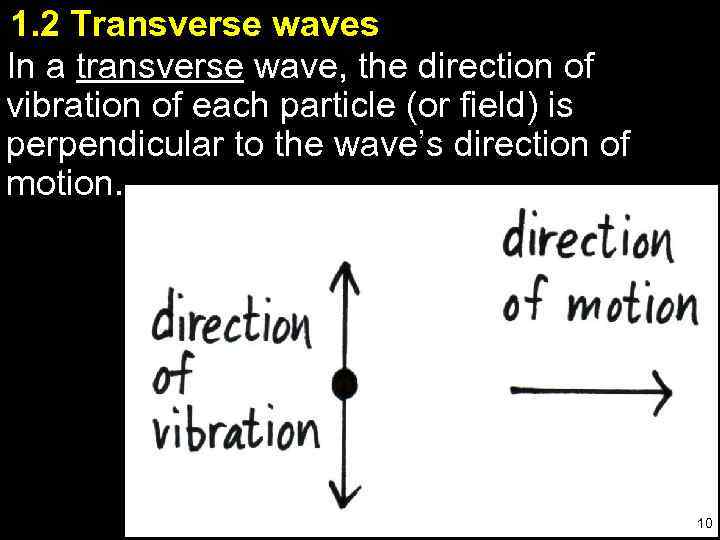1. 2 Transverse waves In a transverse wave, the direction of vibration of each particle (or field) is perpendicular to the wave’s direction of motion. 10

Transverse Waves 11

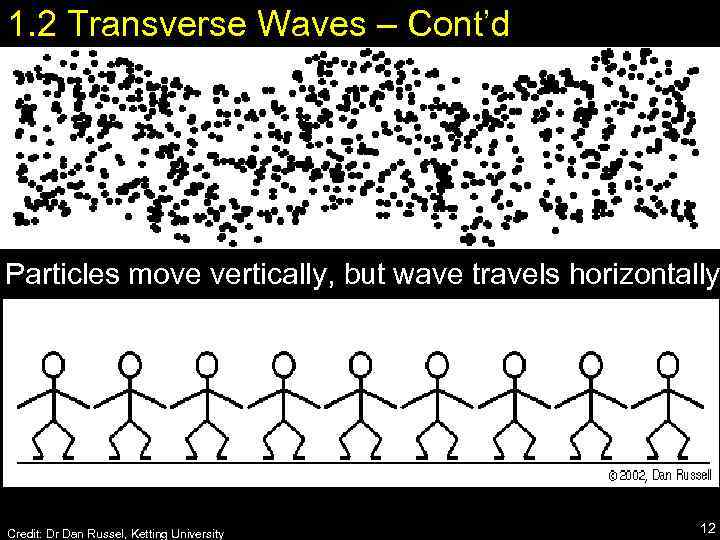1. 2 Transverse Waves – Cont’d Particles move vertically, but wave travels horizontally Credit: Dr Dan Russel, Ketting University 12

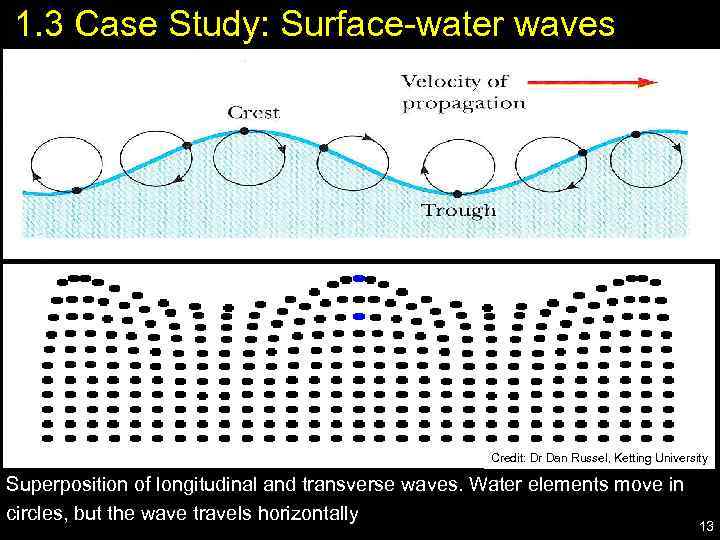1. 3 Case Study: Surface-water waves Credit: Dr Dan Russel, Ketting University Superposition of longitudinal and transverse waves. Water elements move in circles, but the wave travels horizontally 13

1. 4 Types of waves – Brief Review Progressive or Standing Waves Transverse Longitudinal Mechanical Non-Mechanical Provide a definition and an example for each type of wave listed above 14

Mechanical and Electromagnetic (EM) waves A mechanical wave requires a propagation medium, and it can also be a transverse, longitudinal, progressive or standing wave; EM waves do not need a propagation medium. EM waves are always transverse, but they could also be stationary or progressive. 15

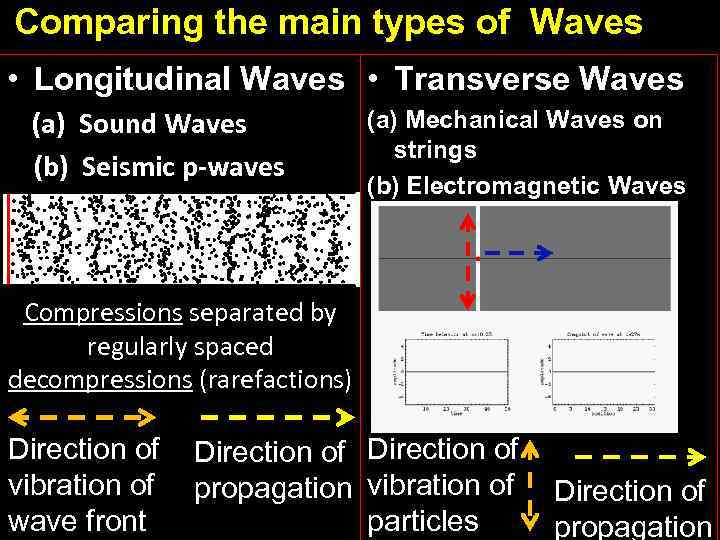Comparing the main types of Waves • Longitudinal Waves • Transverse Waves (a) Sound Waves (b) Seismic p-waves (a) Mechanical Waves on strings (b) Electromagnetic Waves Compressions separated by regularly spaced decompressions (rarefactions) Direction of vibration of propagation vibration of Direction of wave front particles propagation

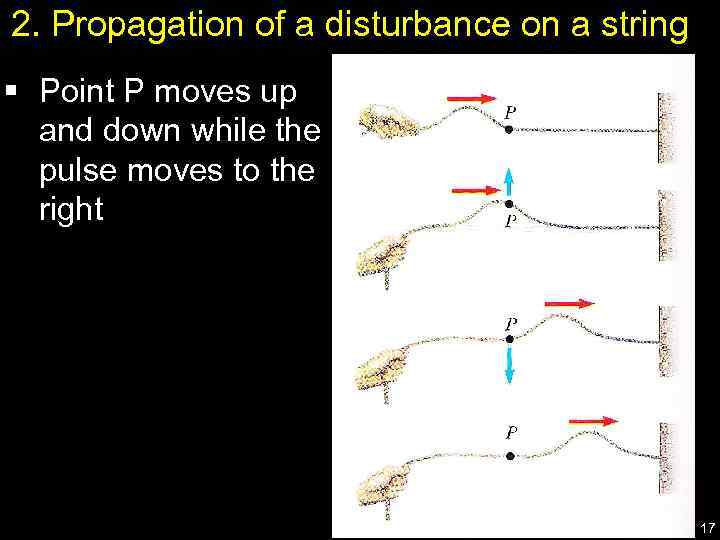2. Propagation of a disturbance on a string § Point P moves up and down while the pulse moves to the right 17

18

19

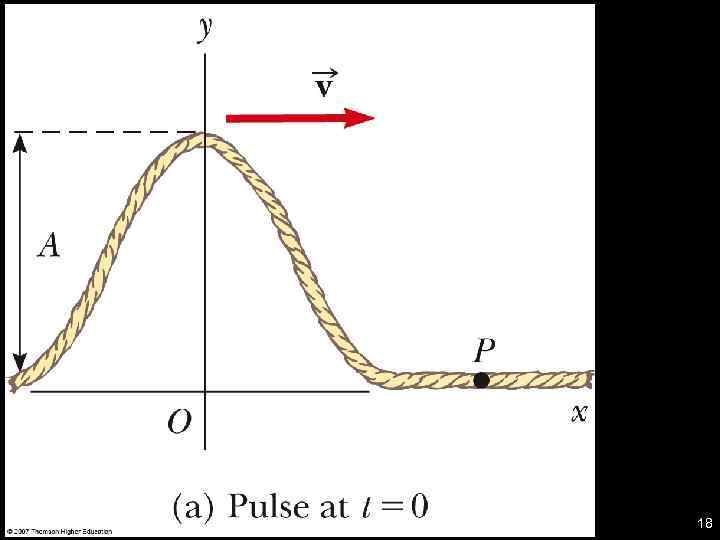
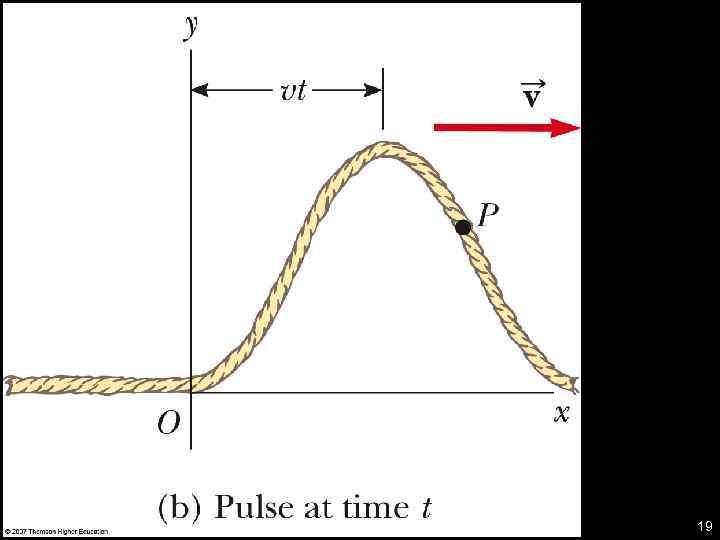
Propagation of a disturbance on a string ■ The wave function y(x, t) representing the transverse position of any element of string at any point of coordinate x and at any time t is given by: for a pulse travelling towards the positive x-axis at speed v. ■ Similarly: for a pulse travelling towards the negative xaxis. ● Here, the function f represents the shape of the pulse at time t = 0. 20

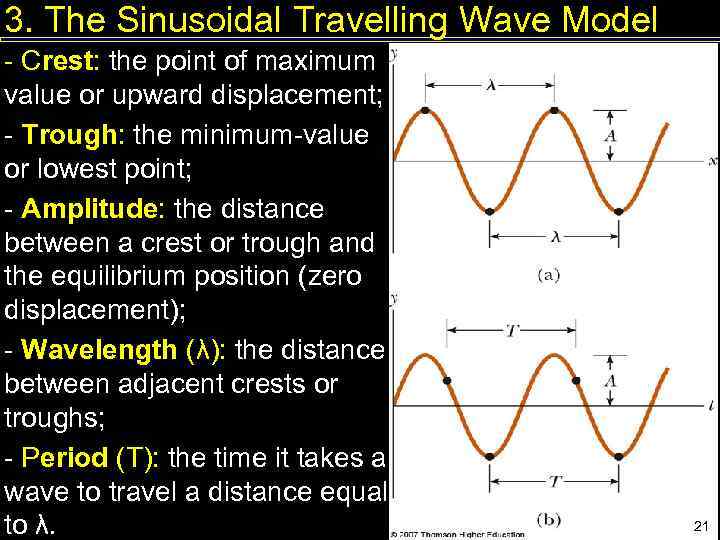3. The Sinusoidal Travelling Wave Model - Crest: the point of maximum value or upward displacement; - Trough: the minimum-value or lowest point; - Amplitude: the distance between a crest or trough and the equilibrium position (zero displacement); - Wavelength (λ): the distance between adjacent crests or troughs; - Period (T): the time it takes a wave to travel a distance equal to λ. 21

3. 1 The progressive wave equation • The simplest wave is sinusoidal; • Let x be the distance measured in the direction of travel and y the particle displacement; • Suppose that y = 0 at x = 0 22

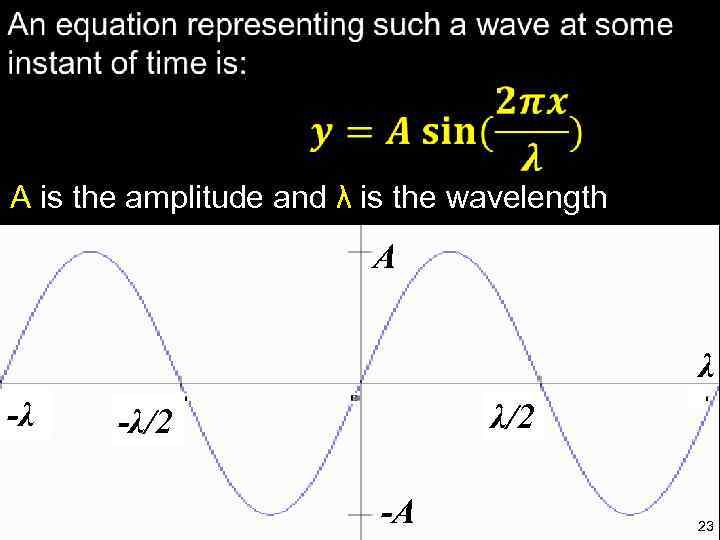A is the amplitude and λ is the wavelength A λ -λ λ/2 -A 23

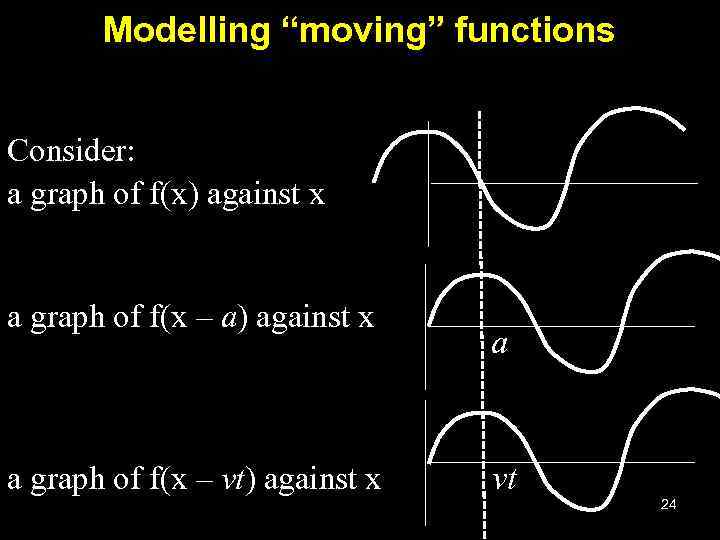Modelling “moving” functions Consider: a graph of f(x) against x a graph of f(x – a) against x a graph of f(x – vt) against x a vt 24

The equation of a moving sine wave The wave travels a distance x = λ in a time t = T Then: The frequency of a wave is the number of complete waves passing a given point in a second 25

Example 1 What is the frequency of visible light of wavelength 0. 500 μm? 26

The general travelling wave equation For waves travelling in the positive x-direction For waves travelling in the negative x-direction is the phase of the wave and φ is the initial phase or phase shift or arbitrary phase difference 28

3. 2 Waves and SHM • In general, every point on the wave undergoes Simple Harmonic Motion (SHM); • For any point with x ≠ 0 the displacement y is a harmonic function of both time and distance from the origin; • At a particular x as x can be treated as a constant. This is the SHM equation; • NOTE: Although the wave travels at constant speed, each point in the wave is in SHM. The SHM period is the same as that of the wave. 29

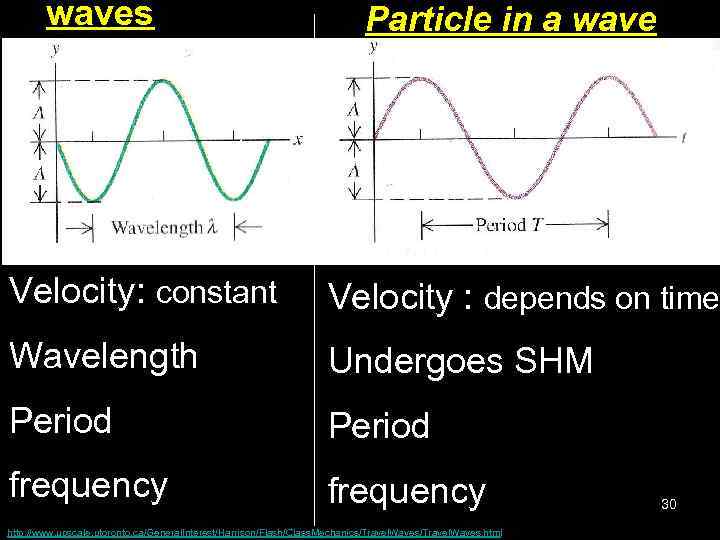waves Particle in a wave Velocity: constant Velocity : depends on time Wavelength Undergoes SHM Period frequency http: //www. upscale. utoronto. ca/General. Interest/Harrison/Flash/Class. Mechanics/Travel. Waves. html 30

Example 2 Starting with the general travelling wave equation, derive expressions for the velocities and accelerations of the oscillating particles of the wave 31

Example 3 A sinusoidal wave is described by the following equation: With y and x in cm and t in s (a) Find the frequency, wavelength and speed of propagation of this wave; At x = 2. 0 cm and t = 2. 0 s; Find (b) the velocity of a particle (c) the acceleration of a particle (d) Calculate the maximum speed(s) and acceleration(s). 32

READING: - Adams and Allday: Section 6. 1; - Serway & Vuille: pages 340 -344. 33

LECTURE CHECKLIST At the end of this lecture you should: • know what is a wave; • be able to define each type of wave and provide at least one example of each type of wave; • know how waves are produced and propagate on strings; • know what is meant by the sinusoidal wave model and what are its properties; • be able to write a mathematical expression that describes a wave travelling in one dimension; • be able to define and identify the wavelength, period, frequency, crest, trough, amplitude and velocity for any one-dimensional wave and know how to use the equation v=f ; • know what is the phase of a wave; • be able to write an equation for the displacement of a particle on a travelling wave, and use that equation to derive equations for the particle’s velocity and acceleration; • be able to sketch the displacement, velocity and acceleration of particles on travelling waves. 34