Л 14 Изопроцессы в газах Среди разнообразных термодинамических

Л 14 Изопроцессы в газах Среди разнообразных термодинамических процессов обычно выделяют процессы, проходящие в условиях постоянства того или иного параметра системы: 1

на вакуумных установках при непрерывной откачке выделяющихся газов могут быть осуществлены как изохорные, так и изобарные условия. изохорные условия В том случае, когда скорость откачки много меньше скорости газовыделения, технологический процесс можно считать протекающим при V = const, где V объем вакуумной камеры. 2

изобарные условия В том случае, когда скорость откачки много больше скорости газовыделения имеет место условие Р = const, где Р – предельное давление вакуумного насоса. 3

• адиабатические (изэнтропные) процессы, протекающие в условиях идеальной тепловой изоляции тела, когда d. Q = Td. S = 0, так что S - const. • изотермические процессы, протекающие в условиях идеального теплового контакта с термостатом, когда тело принимает его температуру Т = const, при этом d. Q = Td. S 0 4

• изохорные процессы, протекающие в условиях постоянства объема системы V = const, так что Pd. V = 0; • изобарные процессы, протекающие в условиях постоянства давления Р = const, при этом d. A = Pd. V 0. 5

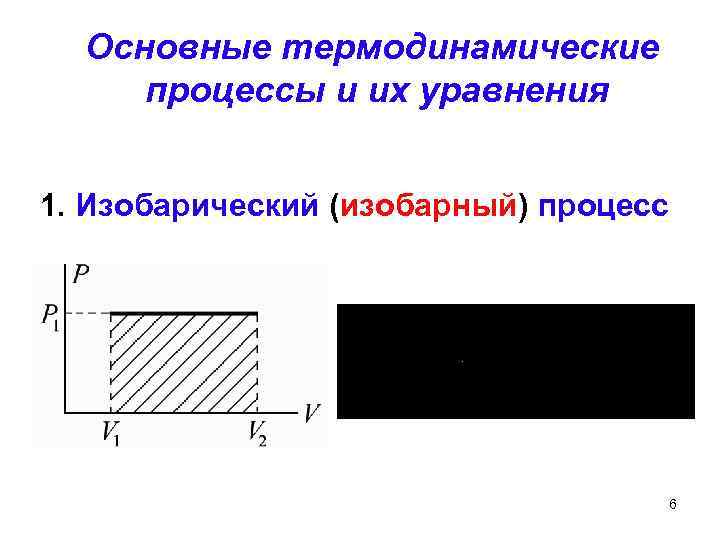
Основные термодинамические процессы и их уравнения 1. Изобарический (изобарный) процесс 6

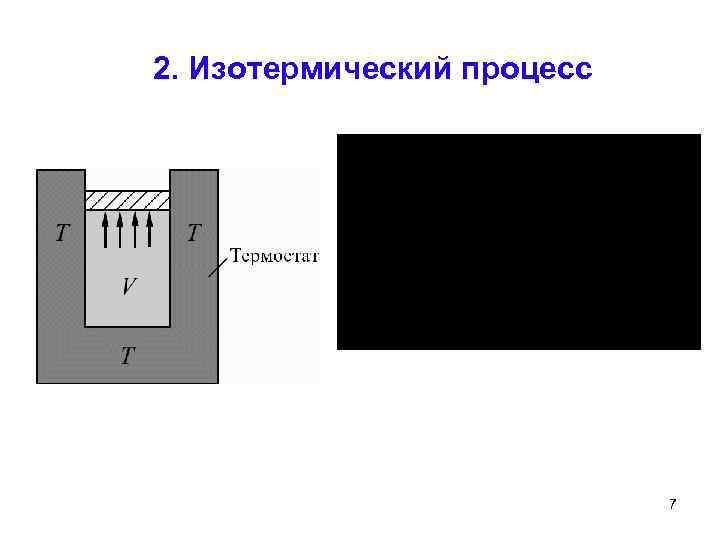
2. Изотермический процесс 7

3. Адиабатный процесс 8

9

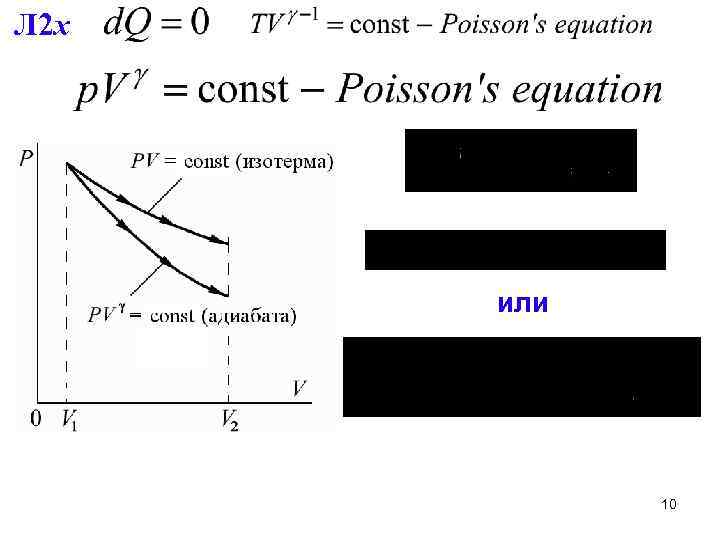
Л 2 x или 10

4. Изохорный процесс 11

Изобарный процесс Для изобарного расширения по первому закону термодинамики имеем Термодинамическую функцию называют энтальпией H: 12

энтальпия 13

Политропические процессы Политропическими называются процессы, при которых теплоемкость тела остается постояной Уравнение политропы для идеального газа Уравнение для I начала термодинамики или: и с учетом того, что учитывая получаем: и разделив на p. V имеем 14

интегрируя введя обозначение имеем - уравнение политропы - показатель политропы 15

При C=CV имеем откуда следует, что V в ходе процесса остается постоянной. Т. о, процесс при C=CV является изохорическим. Показатель полиропы при изохорическом процессе n = Изопроцессы относятся к категории политропических процессов. Процесс n Изобарический 0 Изотермический 1 Адиабатический Изохорический 16

Уравнение для теплоемкости идеального газа при политропическом процессе Частными случаями политропического процесса являются: n=0; изобарический C = CР, n=1; изотермический С = ± , n= ; изохорный C = CV, n= ; изоэнтропийный (адиабатический) С = 0. 17

уравнение политропы в переменных Т и V Исключая из него Т с помощью уравнения состояния T = PV/R, находим при С = 0 n = , данное уравнение соответствует уравнению адиабаты; при С = ± n = 1, получаем уравнение изотермы; при C = CP n = 0 – уравнение изобары; при С = СV n = ± – уравнение изохоры. 18

продифференцируем уравнение политропы , откуда Подставляя данное уравнение в имеем 19

Работа газа при политропических процессах Работу можно вычислить с помощью формулы: Эту же работу можно вычислить с помощью I начала термодинамики: где Т = Т 2 – Т 1 известно Для молей имеем: и При политропических процессах работа газа 20

Тепловая машина Основными элементами любой тепловой машины являются нагреватель, рабочее тело, холодильник Q Рабочее тело – это часть тепловой машины, которая принимает тепло, подводимое к тепловой машине в течение каждого кругового процесса (цикла) рабочее тело Согласно первому началу термодинамики, все количество тепла, подведенное к ТС за цикл, расходуется на совершение работы При этом, если Ao>0 , то цикл называют прямым, иначе – обратным (Ao<0) Задачей тепловой машины, работающей по прямому циклу (Тм. П) является совершение работы A над внешними телами за счет подведенного тепла Q 1 Величину η называют коэффициентом полезного действия Тм. П N 1 21

Идеальная тепловая машина Идеальной тепловой машиной называется тепловая машина, рабочее тело которой совершает круговой процесс, описываемый циклом Карно Цикл Карно – это круговой процесс, состоящий из: двух изотерм - 1→ 2, 3→ 4 и двух адиабат - 2→ 3, 4→ 1 P 2 Изотермический процесс - идеален для теплообмена (CT = ∞) Адиабатический процесс - идеален для изменения внутренней энергии рабочего тела (A = -ΔU) 4 3 V Q 2 Идеальная Тм. П Согласно диаграмме цикла Карно, для Q 1 1 Тм. П первое начало N 1 N 2 коэффициент полезного действия идеальной Тм. П 22

Второе начало термодинамики Второе начало определяет условия, при которых возможны превращения одних видов энергии в другие , а также возможные направления протекания процессов. второе начало термодинамики Клаузиус (1850): невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому телу Кельвин (1851): невозможны процессы, единственным конечным результатом которых было бы превращение тепла целиком в работу. невозможен вечный двигатель 2 -го рода или невозможно создать тепловой двигатель с КПД η = 1 23

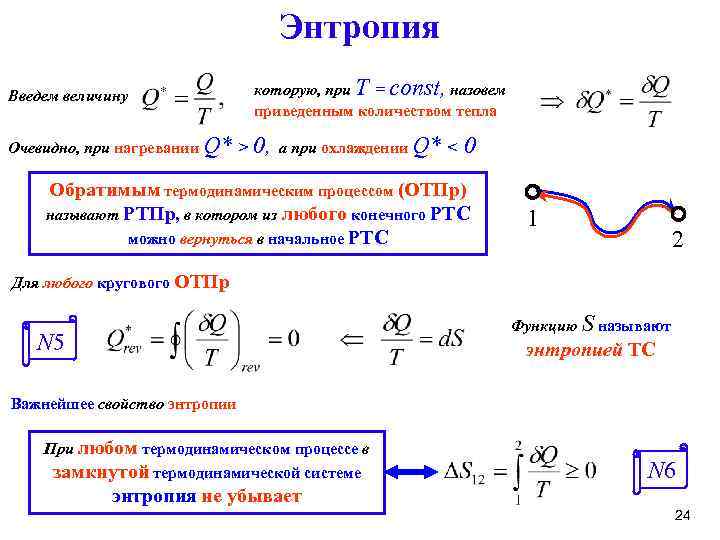
Энтропия Введем величину которую, при T = const, назовем приведенным количеством тепла Очевидно, при нагревании Q* > 0, а при охлаждении Q* < 0 Обратимым термодинамическим процессом (ОТПр) называют РТПр, в котором из любого конечного РТС можно вернуться в начальное РТС 1 2 Для любого кругового ОТПр Функцию S называют N 5 энтропией ТС Важнейшее свойство энтропии При любом термодинамическом процессе в замкнутой термодинамической системе N 6 энтропия не убывает 24

Энтропия и внутренняя энергия Т. о. , первое начало термодинамики для ОТПр принимает вид Тогда для элементарной работы можно написать где введено обозначение: – свободная энергия ТС Из N 7 очевидно, что при T = const N 7 следовательно при изотермическом процессе работа равна убыли свободной энергии С помощью свободной энергии F, внутреннюю энергию U можно найти, как при этом произведение TS называют связанной энергией Связанная энергия это та часть внутренней энергии TC, которая не может быть передана TC в виде работы (при T = const) 25

Понятие энтропии было впервые введено Рудольфом Клаузиусом в 1865 г. Для обратимых процессов изменение энтропии это выражение называется равенством Клаузиуса. 26

Клаузиус Рудольф Юлиус Эмануэль (1822 – 1888) немецкий физиктеоретик, один из создателей термодинамики и кинетической теории газов. 27

Свойства энтропии 1. Энтропия — функция состояния. Если процесс проводят вдоль адиабаты, то энтропия системы не меняется. Значит адиабаты — это одновременно и изоэнтропы. 2. Энтропия — величина аддитивная: энтропия макросистемы равна сумме энтропии ее отдельных частей. 3. Энтропия замкнутой (т. е. теплоизолированной) макросистемы не уменьшается — она либо возрастает, либо остается постоянной. 28

Теорема Нернста (1906) приближении температуры к абсолютному нулю энтропия макросистемы также стремится к нулю: можно вычислять абсолютное значение энтропии по формуле Отсюда следует, что при Т 0 теплоемкость Сp всех макросистем должна тоже стремиться к нулю Теорема Нернста не может быть логически выведена из первых двух начал, поэтому ее часто называют третьим началом термодинамики. 29

вычисление энтропии Основное уравнение термодинамики: т. к. Энтропия идеального газа. Если начальное и конечное состояния, газа 1 и 2, то здесь учтено Взяв дифференциал логарифма от v. RT = p. V, получим и Проинтегрировав последнее выражение, имеем: 30

Цикл Карно рассмотрел цикл из двух изотерм и двух адиабат. Данный цикл является обратимым (если его проводить бесконечно медленно). На S - T диаграмме цикл Карно имеет вид прямоугольника. Полученное тепло равно площади под отрезком 1 -2 Отданное холодильнику тепло равно площади под отрезком 4— 3 равна работе А, Площадь прямоугольника, т. е. совершаемой двигателем за цикл. КПД цикла Карно: 31

Третье начало термодинамики Идеальная тепловая машина работает по циклу Карно и, следовательно, является обратимой ТС Это означает, что для идеальной Тм. П формулу N 2 для к. п. д. идеальной тепловой машины можно записать в виде, где T 1 и S 1 T 2 - температуры нагревателя и холодильника, соответственно вечным двигателем 3 -го рода называют тепловую машину, температура холодильника которой равна нулю T 2 =0 K Принцип Нернста При любом изотермическом процессе (T=const), проведенном при T→ 0 Формулировка Планка ΔST→ 0 = 0 (т. е. S = const δQ = Td. S = 0) При температуре абсолютного нуля (T=0 невозможен такой ТП, в результате которого тело можно охладить до температуры T =0 K K) энтропия любой ТС S= 0 вечный двигатель 3 -го рода невозможен 32

Статистический смысл энтропии 33

Макросостояние – это состояние вещества, характеризуемое его термодинамическими параметрами. Состояние же системы, характеризуемое состоянием каждой входящей в систему молекулы, называют микросостоянием. Так как молекулы движутся хаотически, то имеется много микросостояний, соответствующих одному макросостоянию. Обозначим число микросостояний соответствующее данному макросостоянию (как правило >> 1). 34

Термодинамической вероятностью или статистическим весом макросостояния называется число микросостояний, осуществляющих данное макросостояние (или число перестановок одноименных элементов, при которых сохраняется данное макросостояние). Термодинамическая вероятность максимальна, когда система находится в равновесном состоянии. 35

В состоянии равновесия в термодинамике вероятность максимальна и энтропия максимальна. Из этого можно сделать вывод, что между ними существует связь. Энтропия S – аддитивная величина: , где сумма энтропий тел, входящих в систему. 36

Вероятность сложного события, есть произведение вероятностей где 1 – первое состояние; 2 – второе состояние. Поэтому аддитивной величиной является логарифм : - термодинамическая вероятность или статистический вес. 37

Поэтому Больцман предложил где k – коэффициент Больцмана. С этой точки зрения энтропия выступает, как мера беспорядочности, хаотичности состояния. Например, в ящике черные и белые шары. Они порознь, есть порядок и невелика. После встряхивания – шары перемещаются и – увеличивается и энтропия тоже. 38

И сколько бы не встряхивать потом ящик, никогда черные шары не соберутся у одной стенки, а белые у другой, хотя эта вероятность не равна нулю. Связь между S и позволяет несколько иначе сформулировать второе начало термодинамики: наиболее вероятным изменением энтропии является ее возрастание. 39

Энтропия и вероятность. Расширение идеального газа в пустоту газ идеальный, А = 0, Q = 0, т. е. U =0 T = const приращение энтропии в процессе V 1 - V 2 : где N— число молекул в газе. 1) вероятность обратимся к вероятностям нахождения одной молекулы газа в объеме V 1 равна V 1/V 0 ; Вероятность всех N молекул собраться в объеме V 1 равна Соответственно в объеме V 2 40

отношение этих вероятностей: приращение энтропии : Поскольку вероятность макросистемы пропорциональна ее статистическому весу, т. е. P , имеем: и мы приходим к знаменитой формуле Больцмана Принцип возрастания энтропии со статистической точки зрения привел Больцмана к фундаментальному выводу: все замкнутые макросистемы стремятся переходить от состояний менее вероятных к более вероятным. 41

Энтропия – вероятностная статистическая величина. И утверждение о возрастании энтропии потеряло свою категоричность. Её увеличение вероятно, но не исключаются флуктуации. На этих рассуждениях Клаузиус в 1867 г. и выдвинул гипотезу о тепловой смерти Вселенной Л. Больцман один из первых опроверг эту гипотезу и показал, что закон возрастания энтропии – статистический закон, т. е. возможны отклонения. 42

Энтропия системы – максимальна, при достижении замкнутой системой равновесного состояния. 43