L 14 - Energy in SHM LECTURE OUTLINE 1. Energy in Simple Harmonic Motion; 2. Simple Harmonic and Uniform Circular Motion; 3. Damped Oscillations; 4. Forced Oscillations and Resonance. 1
Project announcement • You have only 2 lab days to take distance v/s voltage readings. • Group leaders MUST submit their windmills in the Newton’s lab at 4. 00 pm on Monday 24 th Nov. • No extension of deadline is permitted.
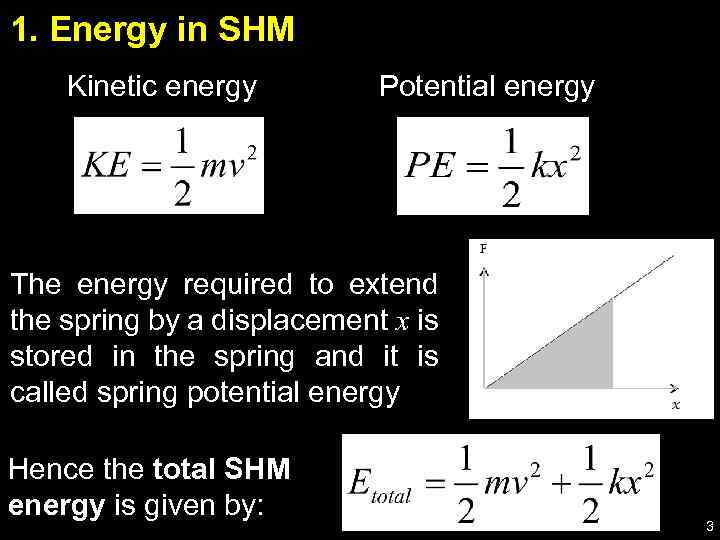1. Energy in SHM Kinetic energy Potential energy The energy required to extend the spring by a displacement x is stored in the spring and it is called spring potential energy Hence the total SHM energy is given by: x 3
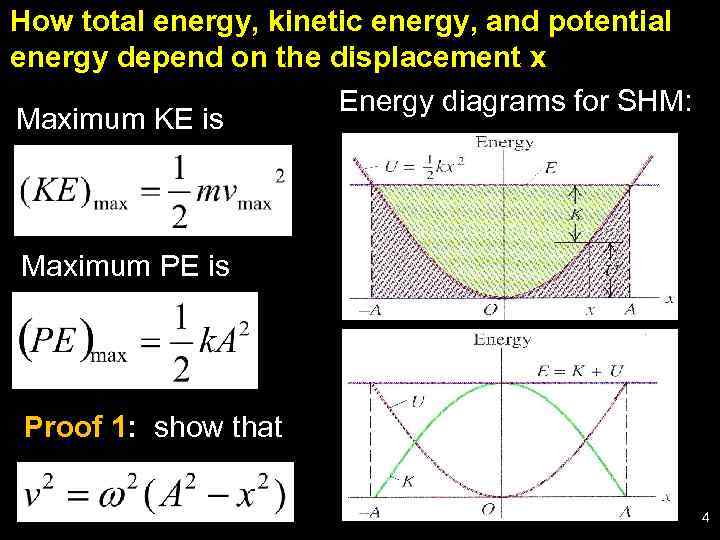How total energy, kinetic energy, and potential energy depend on the displacement x Energy diagrams for SHM: Maximum KE is Maximum PE is Proof 1: show that 4
Example 1 A 0. 500 kg object, attached to a vertical spring of k = 0. 200 k. N/m, is initially in equilibrium. The object is then pulled downwards over a distance of 2. 00 cm and released so that it undergoes SHM. When the object has travelled halfway between the equilibrium position and the release point calculate: a) velocity b) net acceleration c) total SHM energy d) kinetic energy e) spring potential energy 5
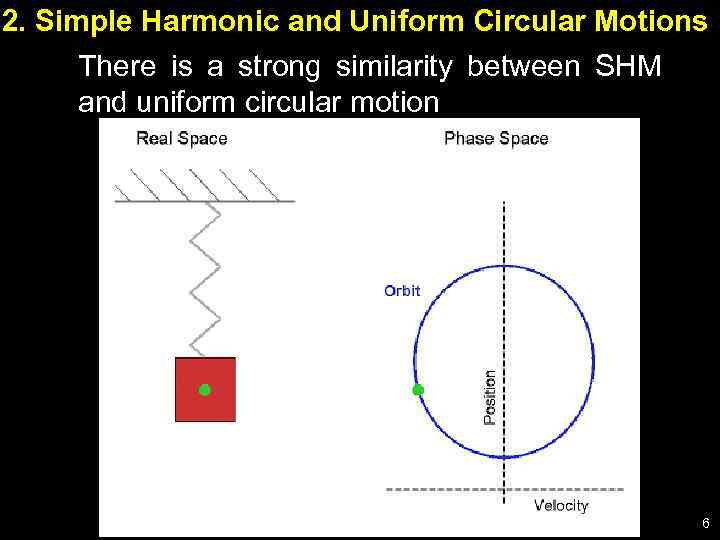2. Simple Harmonic and Uniform Circular Motions There is a strong similarity between SHM and uniform circular motion 6
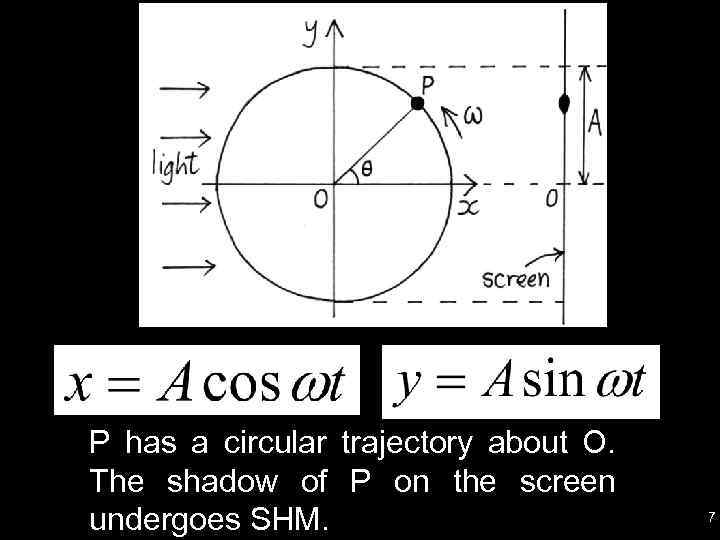P has a circular trajectory about O. The shadow of P on the screen undergoes SHM. 7
3. Damped oscillations SHM is more realistic if it includes friction, air resistance, etc. (damping). The equation of motion becomes: Proof 2: show that the total rate of energy loss is equal to the power dissipated through friction: 8
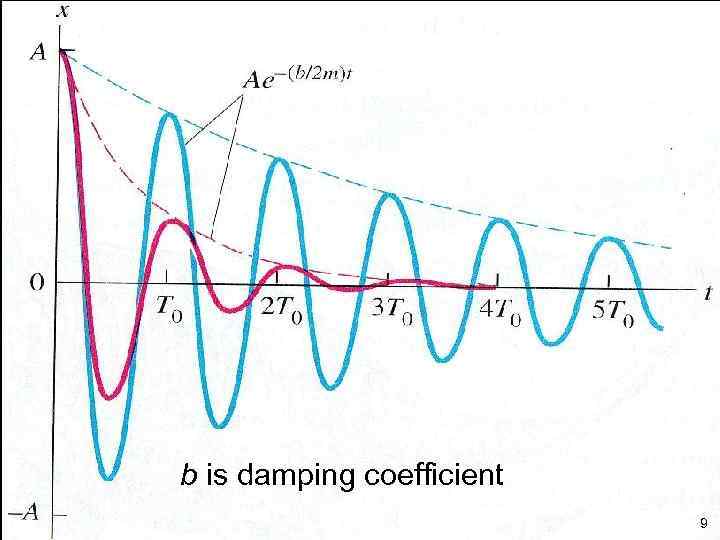b is damping coefficient 9
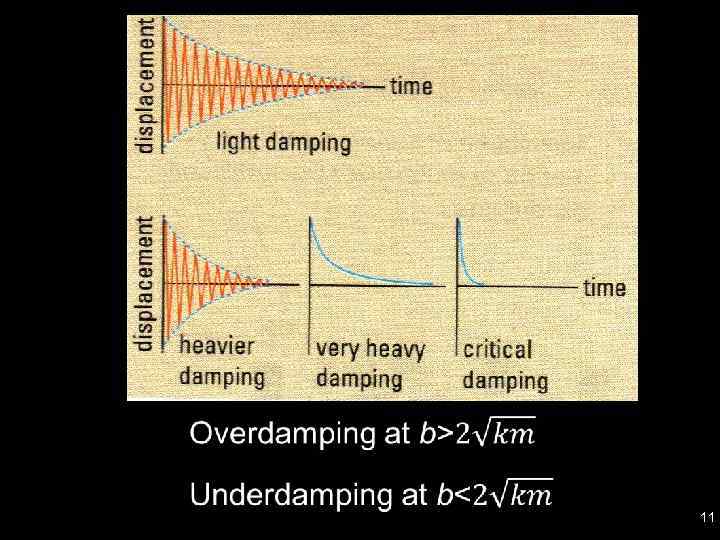
Examples of damping • A car’s suspension system; • Shock absorbers on a mountain bike; • Friction slowing down a pendulum; • Electromagnetic damping. 10
11
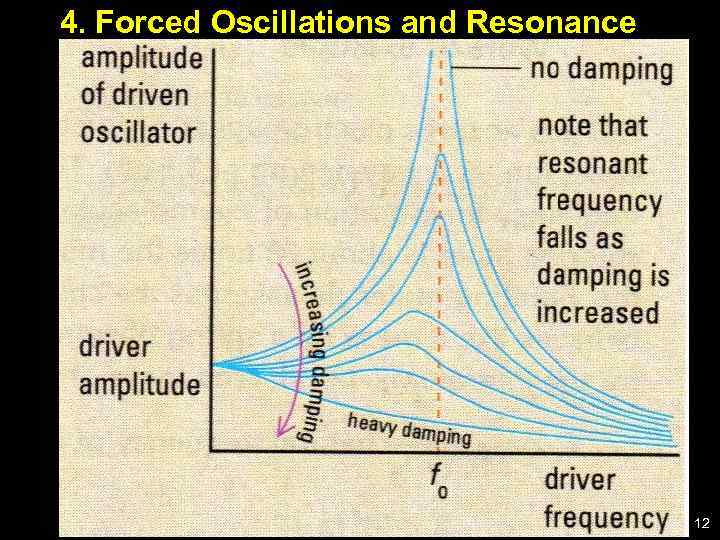4. Forced Oscillations and Resonance 12
Periodic Driving Force Apply a periodic force to a damped system undergoing SHM at its natural frequency. Consider a periodic force And the equation of motion becomes: 13
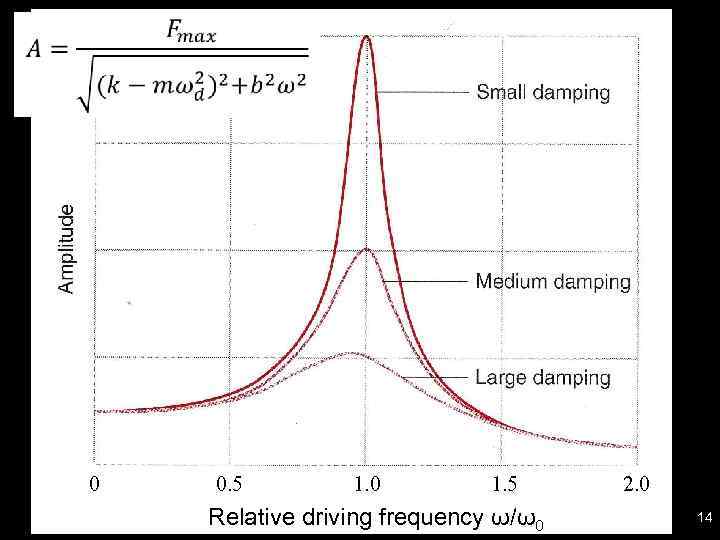0 0. 5 1. 0 1. 5 Relative driving frequency ω/ω0 2. 0 14
Web Interactive. Example: of driven simple harmonic oscillator: http: //www. upscale. utoronto. ca/General. Interest/Harrison/Flash/Class. Mechanics/Drive n. SHM/Driven. SHM. html 15
Resonance • Resonance (highest amplitude peak) occurs when the driving frequency, ω, equals the natural frequency, ω0; • Amplitude increases as damping decreases; • The amplitude vs. frequency curve (resonance curve) broadens as damping increases; • The shape of the resonance curve depends on the damping coefficient b. 16
Example 2 A free swing is a lightly damped system. If a girl starts swinging from a amplitude A = 50. 0 cm with a frequency 0. 500 Hz, calculate the maximum damping force if the damping coefficient is 58. 3 N s m-1 17
Examples of resonance • Bridge collapse due to turbulent winds; • Collapse of buildings following earthquakes; • Nuclear Magnetic Resonance (NMR); • Magnetic Resonance Imaging (MRI); • Electron Spin Resonance (ESR); • Children on swings; • Singing or playing a musical instrument. 18
Shattering a wine glass: http: //www. acoustics. salford. ac. uk/feschools/waves/wine 1 video. htm Volgograd Bridge on May 2010: http: //www. youtube. com/watch? v=4 Pnl. DAHW 9 co&feature=related Tacoma Narrows Bridge on July 1940: http: //www. youtube. com/watch? v=Az 503 VJ 6 k. Hw&feature=related 19
• • LECTURE CHECK LIST Understand PE and KE and total energy for SHM; Be able to perform calculations to find the amplitude, period, frequency and angular frequency of objects performing SHM in a variety of situations; Be able to perform calculations involving PE, KE, acceleration velocity, displacement and energy; Understand the links between SHM and circular motion Understand the notions of natural frequency of an oscillating system and the driving frequency of a system Be able to define resonance Give some real examples of resonance Understand what is meant by damping and be able to give examples in which damping occurs 20
READING: Adams and Allday, 3. 32 3. 36 Serway, Chapter 13, Sections 13. 1 13. 4 Answers: Example 1. a) 0. 346 m/s; b) 4. 00 m/s²; c) 4. 00 x 10 ²־ J; d) 3. 00 x 10 ² J; e) 1. 00 x 10 ²־ J. ־ Example 2. 91. 6 N 21