 Л 13 Первое начало термодинамики Q = d. U + pd. V Внутренняя энергия U является функцией состояния и не зависит от того, каким путем система переведена в данное состояние 1
Л 13 Первое начало термодинамики Q = d. U + pd. V Внутренняя энергия U является функцией состояния и не зависит от того, каким путем система переведена в данное состояние 1
 Теплоемкость Экспериментальный факт: внутренняя энергия идеального газа зависит только от температуры Теплоемкость С тела – количество тепла, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин: -теплоемкость Используют понятие удельной c = C/m и молярной cμ = μc = μC/m теплоемкости, где m - масса, μ - молярная масса ТС 2
Теплоемкость Экспериментальный факт: внутренняя энергия идеального газа зависит только от температуры Теплоемкость С тела – количество тепла, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин: -теплоемкость Используют понятие удельной c = C/m и молярной cμ = μc = μC/m теплоемкости, где m - масса, μ - молярная масса ТС 2
 Опыт показывает, что в широком интервале температур теплоемкость C почти не меняется C - константа ТС Понятие теплоемкости (например молярной) позволяет записать первое начало термодинамики для любого РТПр в виде Для изопроцессов особое значение имеют дополнительные определения теплоемкостей: при постоянном объеме - при постоянном давлении 3
Опыт показывает, что в широком интервале температур теплоемкость C почти не меняется C - константа ТС Понятие теплоемкости (например молярной) позволяет записать первое начало термодинамики для любого РТПр в виде Для изопроцессов особое значение имеют дополнительные определения теплоемкостей: при постоянном объеме - при постоянном давлении 3
 теплоемкость при постоянном объеме теплоемкость при постоянном давлении При постоянном объеме d. V = 0 , согласно d. Q = d. U + pd. V имеем и Таким образом: 4
теплоемкость при постоянном объеме теплоемкость при постоянном давлении При постоянном объеме d. V = 0 , согласно d. Q = d. U + pd. V имеем и Таким образом: 4
 Для киломоля газа процесс изобарический PV = RT при P = const уравнение Майера 5
Для киломоля газа процесс изобарический PV = RT при P = const уравнение Майера 5
 Майер, Юлиус Роберт Julius Robert von Mayer 25. 11. 1814 — 20. 03. 1878 Родился в Хайльбруне, Германия (Heilbronn , Deutschland) Умер в Хайльбруне, Германия (Heilbronn , Deutschland) немецкий физик и врач 6
Майер, Юлиус Роберт Julius Robert von Mayer 25. 11. 1814 — 20. 03. 1878 Родился в Хайльбруне, Германия (Heilbronn , Deutschland) Умер в Хайльбруне, Германия (Heilbronn , Deutschland) немецкий физик и врач 6
 при При нагревании при постоянном давлении часть тепла идет на работу, совершаемую расширяющимся телом, а часть - на увеличение его внутренней энергии, тогда как при нагревании при постоянном объеме вся теплота расходуется на увеличение внутренней энергии. 7
при При нагревании при постоянном давлении часть тепла идет на работу, совершаемую расширяющимся телом, а часть - на увеличение его внутренней энергии, тогда как при нагревании при постоянном объеме вся теплота расходуется на увеличение внутренней энергии. 7
 по определению, имеем Согласно первому началу термодинамики при постоянном объеме d. V = 0, Q = d. U , и Отсюда следует, что CV функция состояния При постоянном давлении : т. о. , ( Q)P полный дифференциал от функции H = U +PV, называемой энтальпией. Отсюда: 8
по определению, имеем Согласно первому началу термодинамики при постоянном объеме d. V = 0, Q = d. U , и Отсюда следует, что CV функция состояния При постоянном давлении : т. о. , ( Q)P полный дифференциал от функции H = U +PV, называемой энтальпией. Отсюда: 8
 энтальпия 9
энтальпия 9
 Запишем еще раз уравнение Майера Уравнение Майера хорошо подтверждается экспериментальными данными Если идеальный газ состоит из атомных частиц, обладающих i степенями свободы, то внутренняя энергия одного моля идеального газа будет равна: тогда: Отсюда: 10
Запишем еще раз уравнение Майера Уравнение Майера хорошо подтверждается экспериментальными данными Если идеальный газ состоит из атомных частиц, обладающих i степенями свободы, то внутренняя энергия одного моля идеального газа будет равна: тогда: Отсюда: 10
 Степени свободы Так называют число независимых координат, необходимых для однозначного задания положения молекулы в пространстве. Ориентация гантели определяется заданием трех углов: и - полярный угол θ - азимутальный угол φ - положение гантели относительно собственной оси задается углом ψ 11
Степени свободы Так называют число независимых координат, необходимых для однозначного задания положения молекулы в пространстве. Ориентация гантели определяется заданием трех углов: и - полярный угол θ - азимутальный угол φ - положение гантели относительно собственной оси задается углом ψ 11
 теорема о равнораспределении энергии по степеням свободы средняя кинетическая энергия, приходящаяся при тепловом равновесии на одну степень свободы любой атомно-молекулярной системы равна: 12
теорема о равнораспределении энергии по степеням свободы средняя кинетическая энергия, приходящаяся при тепловом равновесии на одну степень свободы любой атомно-молекулярной системы равна: 12
 Общее число степеней свободы у молекулы складывается из поступательных i 1, вращательных i 2 и удвоенной величины колебательных степеней свободы i 3, поскольку с колебаниями связаны два вида энергии – потенциальная и кинетическая, средние значения которых при гармонических колебаниях равны между собой i = i 1 + i 2 + 2 i 3 13
Общее число степеней свободы у молекулы складывается из поступательных i 1, вращательных i 2 и удвоенной величины колебательных степеней свободы i 3, поскольку с колебаниями связаны два вида энергии – потенциальная и кинетическая, средние значения которых при гармонических колебаниях равны между собой i = i 1 + i 2 + 2 i 3 13
 средняя кинетическая энергия молекулы внутренняя энергия моля идеального газа где 14
средняя кинетическая энергия молекулы внутренняя энергия моля идеального газа где 14
 Отношение называется показателем адиабаты, однозначно определяет обе молярные теплоемкости и представляет характерную для каждого газа величину одноатомные газы двухатомные газы трехатомные газы 15
Отношение называется показателем адиабаты, однозначно определяет обе молярные теплоемкости и представляет характерную для каждого газа величину одноатомные газы двухатомные газы трехатомные газы 15
 откуда сравнивая получаем еще одно уравнение для внутренней энергии Таким образом: определяется числом и характером степеней свободы молекулы 16
откуда сравнивая получаем еще одно уравнение для внутренней энергии Таким образом: определяется числом и характером степеней свободы молекулы 16
 Изопроцессы в газах Среди разнообразных термодинамических процессов обычно выделяют процессы, проходящие в условиях постоянства того или иного параметра системы: 17
Изопроцессы в газах Среди разнообразных термодинамических процессов обычно выделяют процессы, проходящие в условиях постоянства того или иного параметра системы: 17
 на вакуумных установках при непрерывной откачке выделяющихся газов могут быть осуществлены как изохорные, так и изобарные условия. изохорные условия В том случае, когда скорость откачки много меньше скорости газовыделения, технологический процесс можно считать протекающим при V = const, где V объем вакуумной камеры. 18
на вакуумных установках при непрерывной откачке выделяющихся газов могут быть осуществлены как изохорные, так и изобарные условия. изохорные условия В том случае, когда скорость откачки много меньше скорости газовыделения, технологический процесс можно считать протекающим при V = const, где V объем вакуумной камеры. 18
 изобарные условия В том случае, когда скорость откачки много больше скорости газовыделения имеет место условие Р = const, где Р – предельное давление вакуумного насоса. 19
изобарные условия В том случае, когда скорость откачки много больше скорости газовыделения имеет место условие Р = const, где Р – предельное давление вакуумного насоса. 19
 • адиабатические (изэнтропные) процессы, протекающие в условиях идеальной тепловой изоляции тела, когда d. Q = Td. S = 0, так что S - const. • изотермические процессы, протекающие в условиях идеального теплового контакта с термостатом, когда тело принимает его температуру Т = const, при этом d. Q = Td. S 0 20
• адиабатические (изэнтропные) процессы, протекающие в условиях идеальной тепловой изоляции тела, когда d. Q = Td. S = 0, так что S - const. • изотермические процессы, протекающие в условиях идеального теплового контакта с термостатом, когда тело принимает его температуру Т = const, при этом d. Q = Td. S 0 20
 • изохорные процессы, протекающие в условиях постоянства объема системы V = const, так что Pd. V = 0; • изобарные процессы, протекающие в условиях постоянства давления Р = const, при этом d. A = Pd. V 0. 21
• изохорные процессы, протекающие в условиях постоянства объема системы V = const, так что Pd. V = 0; • изобарные процессы, протекающие в условиях постоянства давления Р = const, при этом d. A = Pd. V 0. 21
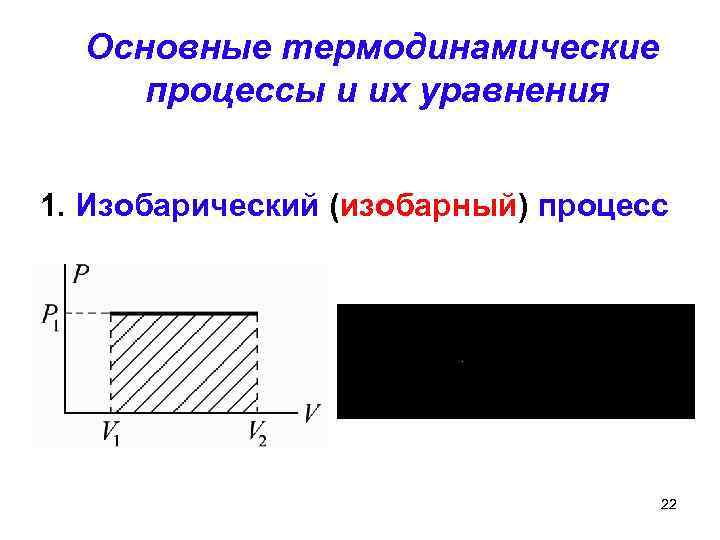 Основные термодинамические процессы и их уравнения 1. Изобарический (изобарный) процесс 22
Основные термодинамические процессы и их уравнения 1. Изобарический (изобарный) процесс 22
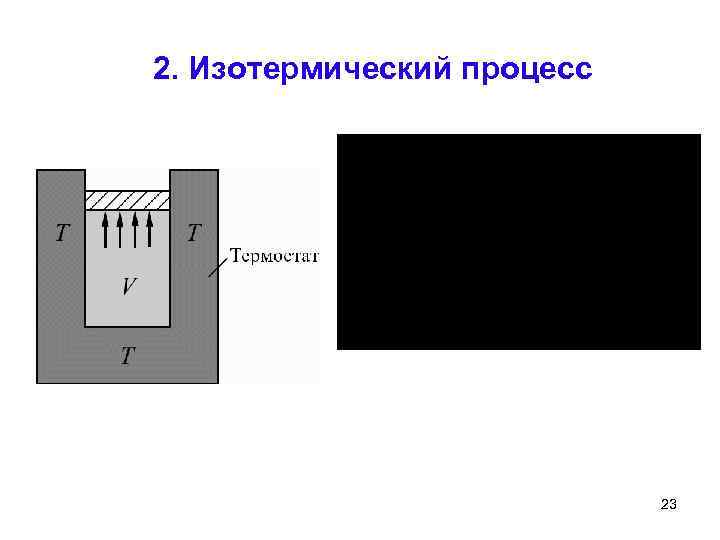 2. Изотермический процесс 23
2. Изотермический процесс 23
 3. Адиабатный процесс 24
3. Адиабатный процесс 24
 25
25
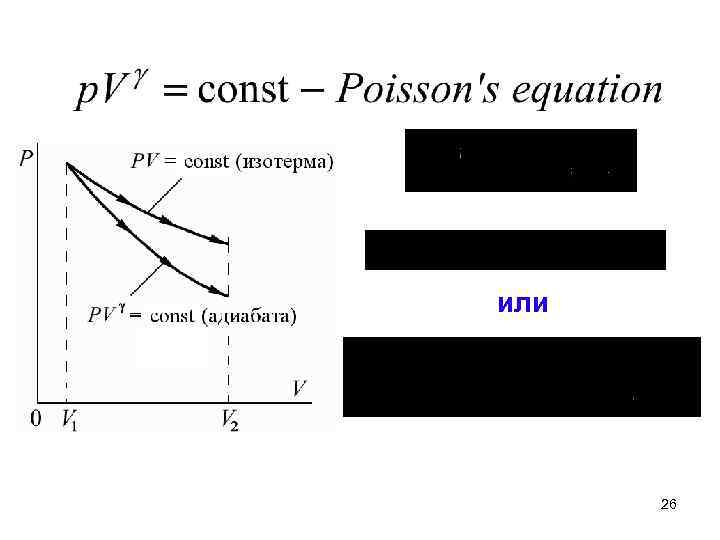 или 26
или 26
 4. Изохорный процесс 27
4. Изохорный процесс 27
 5. Политропический (политропный) процесс, происходящий при С = const. Частными случаями политропического процесса являются: изобарический C = CР, изотермический С = ± , изохорный C = CV, изоэнтропийный (адиабатический) С = 0. теплоемкость в политропическом процессе: тогда: учитывая получаем: где показатель политропы. 28
5. Политропический (политропный) процесс, происходящий при С = const. Частными случаями политропического процесса являются: изобарический C = CР, изотермический С = ± , изохорный C = CV, изоэнтропийный (адиабатический) С = 0. теплоемкость в политропическом процессе: тогда: учитывая получаем: где показатель политропы. 28
 уравнение политропы в переменных Т и V Исключая из него Т с помощью уравнения состояния T = PV/R, находим Продифференцируем , откуда 29
уравнение политропы в переменных Т и V Исключая из него Т с помощью уравнения состояния T = PV/R, находим Продифференцируем , откуда 29
 Подставляя данное уравнение в имеем при С = 0 n = , данное уравнение соответствует уравнению адиабаты; при С = ± n = 1, получаем уравнение изотермы; при C = CP n = 0 – уравнение изобары; при С = СV n = ± – уравнение изохоры. 30
Подставляя данное уравнение в имеем при С = 0 n = , данное уравнение соответствует уравнению адиабаты; при С = ± n = 1, получаем уравнение изотермы; при C = CP n = 0 – уравнение изобары; при С = СV n = ± – уравнение изохоры. 30
 Работа газа при политропических процессах Работу можно вычислить с помощью формулы: Эту же работу можно вычислить с помощью I начала термодинамики: где Т = Т 2 – Т 1 известно Для молей имеем: и При политропических процессах работа газа 31
Работа газа при политропических процессах Работу можно вычислить с помощью формулы: Эту же работу можно вычислить с помощью I начала термодинамики: где Т = Т 2 – Т 1 известно Для молей имеем: и При политропических процессах работа газа 31
 Тепловая машина Основными элементами любой тепловой машины являются нагреватель, рабочее тело, холодильник Q Рабочее тело – это часть тепловой машины, которая принимает тепло, подводимое к тепловой машине в течение каждого кругового процесса (цикла) рабочее тело Согласно первому началу термодинамики, все количество тепла, подведенное к ТС за цикл, расходуется на совершение работы При этом, если Ao>0 , то цикл называют прямым, иначе – обратным (Ao<0) Задачей тепловой машины, работающей по прямому циклу (Тм. П) является совершение работы A над внешними телами за счет подведенного тепла Q 1 Величину η называют коэффициентом полезного действия Тм. П N 1 32
Тепловая машина Основными элементами любой тепловой машины являются нагреватель, рабочее тело, холодильник Q Рабочее тело – это часть тепловой машины, которая принимает тепло, подводимое к тепловой машине в течение каждого кругового процесса (цикла) рабочее тело Согласно первому началу термодинамики, все количество тепла, подведенное к ТС за цикл, расходуется на совершение работы При этом, если Ao>0 , то цикл называют прямым, иначе – обратным (Ao<0) Задачей тепловой машины, работающей по прямому циклу (Тм. П) является совершение работы A над внешними телами за счет подведенного тепла Q 1 Величину η называют коэффициентом полезного действия Тм. П N 1 32
 Идеальная тепловая машина Идеальной тепловой машиной называется тепловая машина, рабочее тело которой совершает круговой процесс, описываемый циклом Карно Цикл Карно – это круговой процесс, состоящий из: двух изотерм - 1→ 2, 3→ 4 и двух адиабат - 2→ 3, 4→ 1 P 2 Изотермический процесс - идеален для теплообмена (CT = ∞) Адиабатический процесс - идеален для изменения внутренней энергии рабочего тела (A = -ΔU) 4 3 V Q 2 Идеальная Тм. П Согласно диаграмме цикла Карно, для Q 1 1 Тм. П первое начало N 1 N 2 коэффициент полезного действия идеальной Тм. П 33
Идеальная тепловая машина Идеальной тепловой машиной называется тепловая машина, рабочее тело которой совершает круговой процесс, описываемый циклом Карно Цикл Карно – это круговой процесс, состоящий из: двух изотерм - 1→ 2, 3→ 4 и двух адиабат - 2→ 3, 4→ 1 P 2 Изотермический процесс - идеален для теплообмена (CT = ∞) Адиабатический процесс - идеален для изменения внутренней энергии рабочего тела (A = -ΔU) 4 3 V Q 2 Идеальная Тм. П Согласно диаграмме цикла Карно, для Q 1 1 Тм. П первое начало N 1 N 2 коэффициент полезного действия идеальной Тм. П 33
 Второе начало термодинамики Второе начало определяет условия, при которых возможны превращения одних видов энергии в другие , а также возможные направления протекания процессов. второе начало термодинамики Клаузиус (1850): невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому телу Кельвин (1851): невозможны процессы, единственным конечным результатом которых было бы превращение тепла целиком в работу. невозможен вечный двигатель 2 -го рода или невозможно создать тепловой двигатель с КПД η = 1 34
Второе начало термодинамики Второе начало определяет условия, при которых возможны превращения одних видов энергии в другие , а также возможные направления протекания процессов. второе начало термодинамики Клаузиус (1850): невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому телу Кельвин (1851): невозможны процессы, единственным конечным результатом которых было бы превращение тепла целиком в работу. невозможен вечный двигатель 2 -го рода или невозможно создать тепловой двигатель с КПД η = 1 34


