L 12 Rotational Dynamics Lecture Outline 1 Moment

L 12. Rotational Dynamics Lecture Outline 1. Moment of inertia 2. Angular momentum 3. Work and Power in Rotational Motion 4. Work-KE Theorem in Rotational Motion 5. Linear and Rotational Motion equations 1 1

1. Moment of Inertia - Consider a rigid body rotating with angular speed ω; - The body is divided into many individual masses, m 1, m 2, etc. , at distances r 1, r 2, etc. , respectively, from the stationary rotation axis or pivot. 2

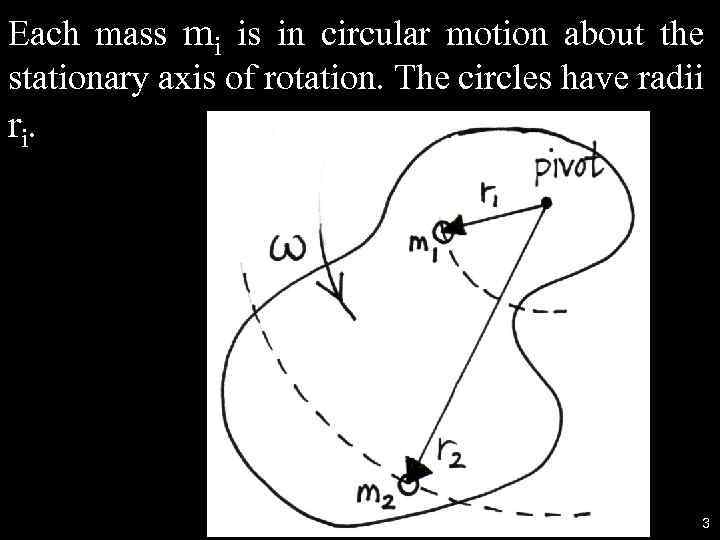Each mass mi is in circular motion about the stationary axis of rotation. The circles have radii ri. 3

Rotational or Angular KE 4

Moment of inertia (I) - definition § I is called the moment of inertia of the body about the chosen axis of rotation: § I is a measure of the distribution of mass about the axis of rotation § [ I ] = M L 2 and its SI units are kg m 2 5

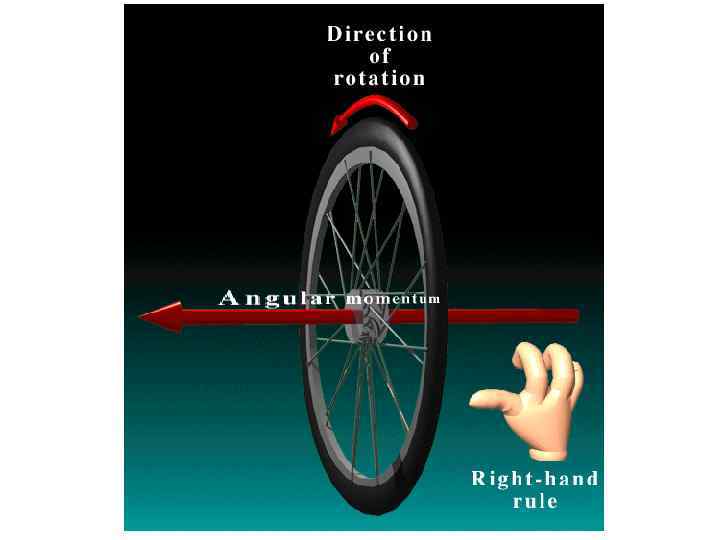
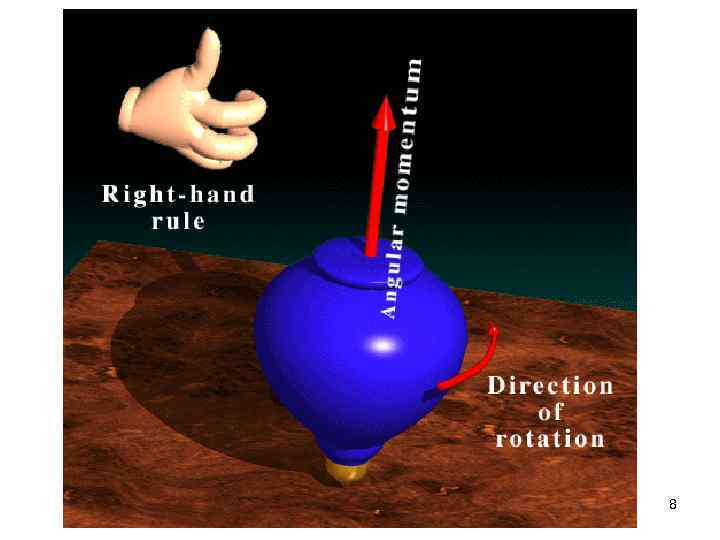
2. Angular momentum § Similar to torque, § the Angular Momentum of a particle of mass m rotating at a distance r about some axis is defined as: where r is the particle’s position vector and linear momentum; its § L is perpendicular to the plane of r and , and its direction is given by the right hand rule. 6

7

8

Angular and Linear momenta • Linear momentum: p = mv • It can be shown that the angular momentum: L = Iω • I is also a measure of an object’s angular inertia 9

Angular Momentum and Torque • It can be shown that: • From which Newton’s second law for rotational motion follows: where the torques and the moment of inertia are calculated about the same axis 10 10

Conservation of Momentum 1) Linear momentum is conserved if the net external force is zero; 2) Angular momentum is conserved if the net external torque is zero. 11

Conservation of angular momentum • L = I ω is constant if there is no net external torque; • As the skater moves her arms closer to her body, ri decrease, I decreases and ω increases. Thus the skater spins faster. 12

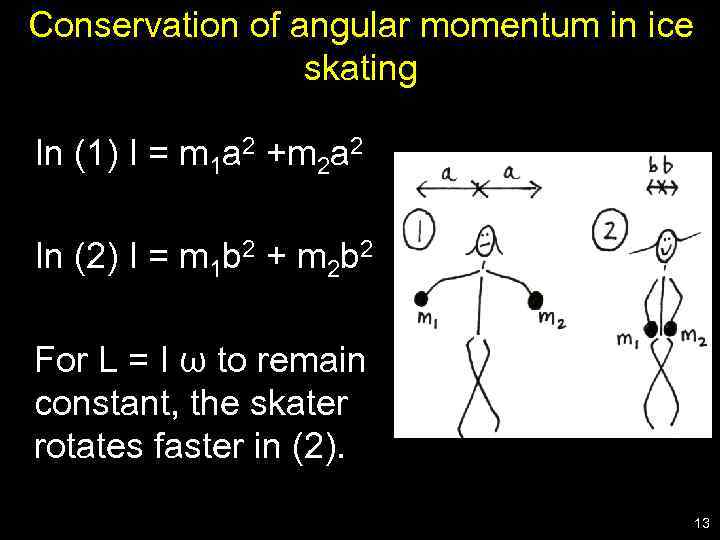Conservation of angular momentum in ice skating In (1) I = m 1 a 2 +m 2 a 2 In (2) I = m 1 b 2 + m 2 b 2 For L = I ω to remain constant, the skater rotates faster in (2). 13

Warning: Attempt at your own risk! A crazy physics teacher stands on a swivel chair with weights in his outstretched arms. A student startles him by rotating the chair. The teacher quickly moves his arms in, and… 14

3. Work and Power in Rotational Motion It can be shown that the work done by a torque t that rotates a rigid object by an angle q : W = tq Then, the power 15

4. Work-Kinetic Energy Theorem § The net work done by external torques rotating a rigid object about a fixed axis equals the change in kinetic energy of the object: § It can be shown that: 16

5. Linear and Angular motion equations 17

Example 1: the motion of a yo-yo § The end of the string of a yo-yo is held stationary and the cylinder (mass M, radius R) is released rest; § The string unwinds but does not slip as the cylinder falls and rotates; § Find the speed v. CM of the centre of mass of the cylinder after it has dropped a distance h. Note: the moment of inertia of the cylinder about an axis passing through its centre of mass is ½MR 2 18

Ex 2. Conservation of angular momentum A horizontal disc rotates freely about a vertical axis at 90. 0 rpm. A 20. 0 g small piece of chewing gum falls onto the disc and sticks to it at a distance of 5. 00 cm from its axis of rotation. The rotation frequency is reduced to 80. 0 rpm. Find the disc’s moment of inertia. 19

Ex 3. Work and Power in Rotational Motion An electric motor supplies a maximum power of 500 W to drive a flywheel of I = 2. 00 kgm 2 at a speed of 600 rev/min. How long will it take the flywheel to come to rest after the power is switched off, assuming the retarding torque, due to friction, is constant? 20

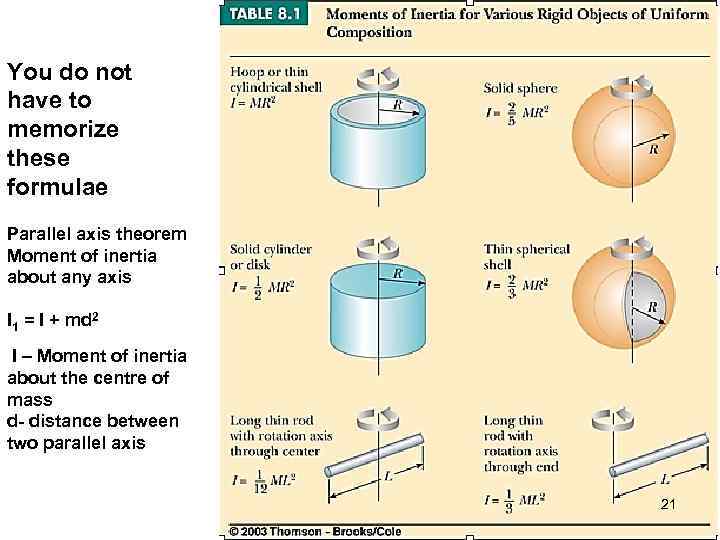You do not have to memorize these formulae Parallel axis theorem Moment of inertia about any axis I 1 = I + md 2 I – Moment of inertia about the centre of mass d- distance between two parallel axis 21

Linear (translational) and Angular (rotational) Motion 22

CHECKLIST READING Adams and Allday: 3. 30, 3. 31 , Serway 8. 5, 8. 6, 8. 7 At the end of this lecture you should • • • Be able to define angular momentum; Be able to define the moment of inertia of a rigid body or system of point particles; Understand the link between angular momentum, moment of inertia and angular speed; Be able to define the work done by a torque rotating a rigid object by an angle and the power delivered by this torque; Know the equation for the kinetic energy of a body rotating with angular speed ; Know the similarity between linear and angular equations of motion and be able to use them. 23

• 24