L 11 Circular Motion Circular Motion

L 11 – Circular Motion • Circular Motion and Angular Velocity • Radial and Tangential Acceleration (Polar Coordinates) • Uniform Circular Motion • Circular Motion Vectors • Centripetal Acceleration • Centripetal Force • Dynamics of Circular Motion • Motion of Satellites 1 1

Announcements: Physics Project Reminder Preliminary Testing is This Week: • Groups 01 - 19 on Tuesday 11 th Nov • Groups 20 – 38 on Thursday 13 th Nov • Groups 39 – 56 on Friday 14 th Nov Your group must have a working Wind generator ready for testing by 4 pm at the latest on these days. 2

Announcements: Course Work Test 2 Wednesday, 12 th November, 4 pm Same rooms as your last CW test. Will cover: Course Works 4, 5 Lectures and PSCs 7, 8, 9, 10 3

Announcements: Support sessions If you sign up for Office Hours – you are required to attend them. If you miss the office hours you signed up for, and do not contact the teacher, you may be unable to sign up for other office hours 4

Circular motion We can now extend the ideas of Newton’s Laws and the conservation of energy to motion in a circle. First, define ω(t) = dθ/dt as the angular velocity. 5

6

Radial and Tangential Acceleration § To derive the expression for the acceleration vector in circular motion, we define polar coordinates § Prove the following equations: 7

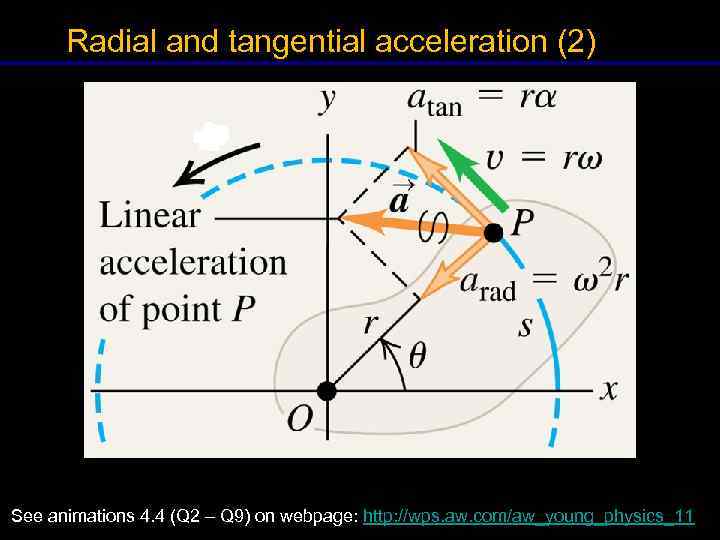Radial and tangential acceleration (2) 8 See animations 4. 4 (Q 2 – Q 9) on webpage: http: //wps. aw. com/aw_young_physics_11

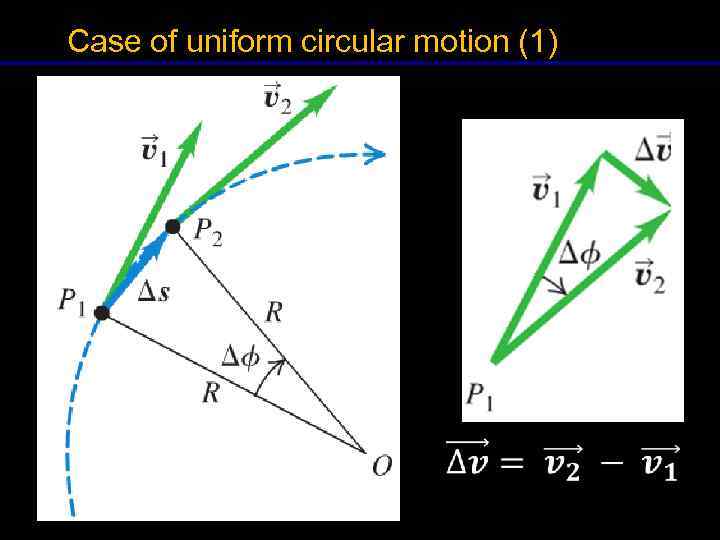Case of uniform circular motion (1) 9

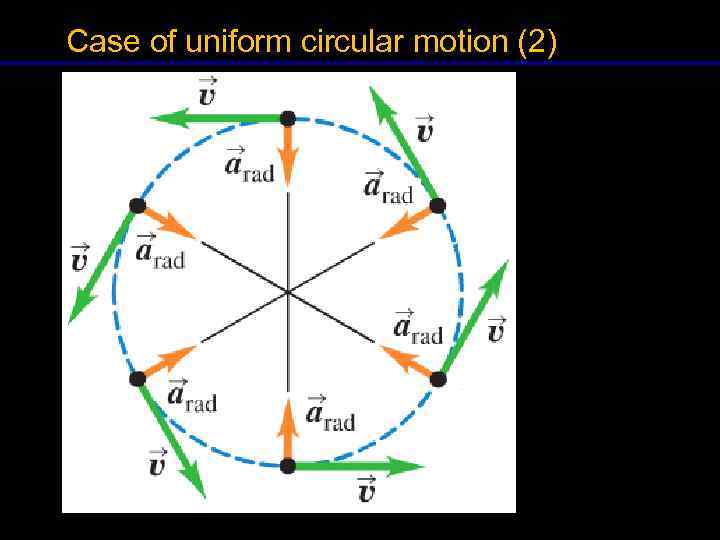Case of uniform circular motion (2) 10

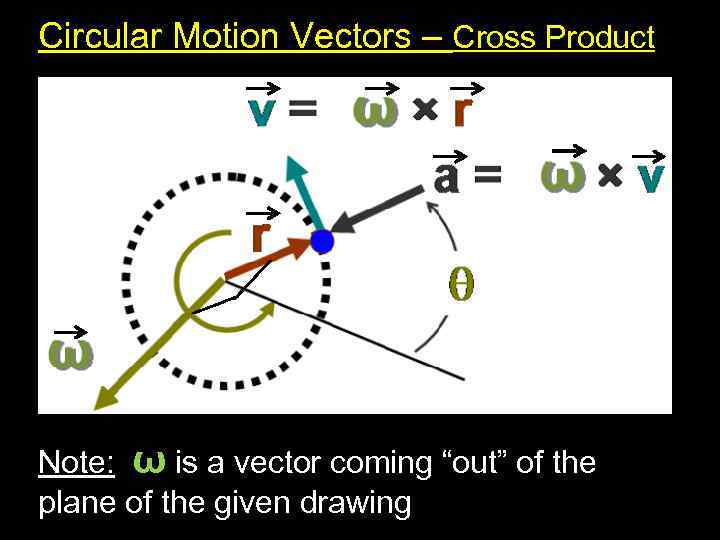Circular Motion Vectors – Cross Product Note: ω is a vector coming “out” of the plane of the given drawing 11

Rotation with constant angular acceleration 12

Centripetal force Clearly, if an object is accelerating there must be a force acting on it. The net force which causes centripetal acceleration is called the centripetal force. The centripetal force is always supplied by some other force or set of forces (e. g. gravitation or tension). It is always directed toward the centre of the circle. 13

Centripetal force 14

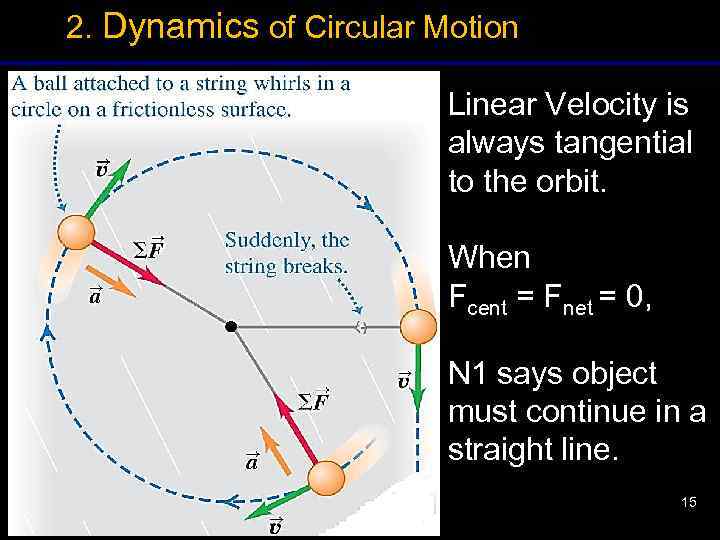2. Dynamics of Circular Motion Linear Velocity is always tangential to the orbit. When Fcent = Fnet = 0, N 1 says object must continue in a straight line. 15 15

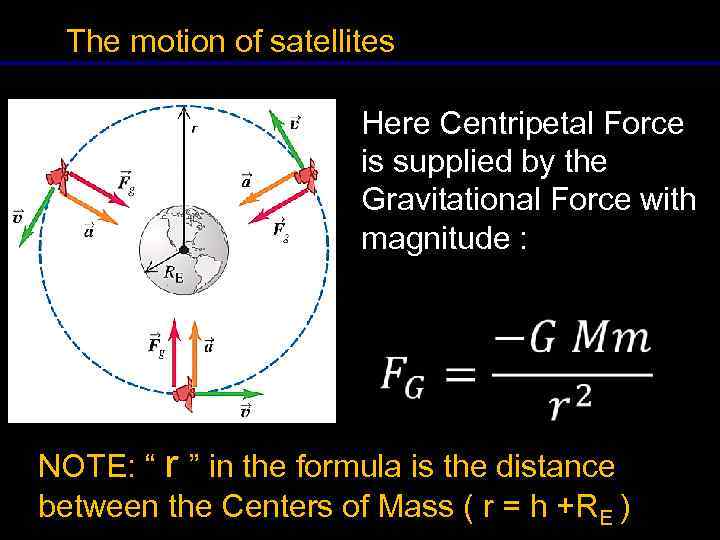The motion of satellites Here Centripetal Force is supplied by the Gravitational Force with magnitude : NOTE: “ r ” in the formula is the distance between the Centers of Mass ( r = h +RE ) 16

Geostationary satellites • A geostationary satellite stays above one point on the Earth’s surface, and thus has a period of 24 hours 17

Example 1: • A tube is placed upon the table and shaped into a three-quarters circle. A golf ball is pushed into the tube at one end at high speed. The ball rolls through the tube and exits at the opposite end. Describe the path of the golf ball as it exits the tube. • Why does the golf ball act in that it way? 18

A turntable rotating at 33. 3 rpm For Example 2: 19

Example 2: A 5 Tenge coin is placed at the edge of a turntable as in the previous image, with diameter d = 30. 0 cm. The turntable makes 33. 3 revolutions per minute. a) draw a free body diagram of the forces acting on the coin b) find the angular speed of the record c) if the coin is 2. 00 g and the maximum Ffriction provided by the turntable is 6. 00 x 10 -4 N, calculate whether the coin will stay on or slip 20 off.

Circular motion for non-constant ω For objects moving in a circle, the angular speed, ω, will generally not be constant. For example: a stone at the end of a string moving in a vertical circle, or a skateboarder in a hemispherical ‘bowl’, an airplane looping the loop! This is because the centripetal force is varying. 21

Example 3: A stone at the end of a piece of string moves vertically with a circular motion about “O”. Its mass is 0. 150 kg, speed at the top is 3. 50 m s-1 and the string is 0. 700 m long. a) Sketch a free body diagram for the stone at the top of the circle b) Find the resultant force on the stone at that position c) Find the tension in the string at that position d) Calculate T when the stone is at the bottom 22 of the circle

CHECK LIST READING Adams and Allday: 3. 28, 3. 29 Serway : 7. 1, 7. 2, 7. 3, 7. 4 At the end of this lecture you should • Be able to define angular speed, centripetal acceleration, centripetal force • Appreciate why an object moving in a circle must have a force acting on it • Understand the direction and nature of both the centripetal force and centrifugal force • Understand how circular motion can arise in a number of different situations in which the force applied to an object is perpendicular to the direction of the object's motion • Appreciate the difference between circular motion of uniform angular speed and circular motion in which the angular speed may be varying • Be able to give examples of such situations and perform calculations to work out various properties of the circular motion in these different cases 23

• Numerical Answers • : Ex 2 - b) 3. 49 rads-1 c) Fcentripetal is supplied by Ffriction. (opposes motion of coin) Therefore if Fcent > 6. 00 x 10 -4 , the coin will slip off. Here ω = 3. 49 rad/sec, and Fcent= (36. 3 x 10 -4), so the coin does indeed slip and flies off tangential to motion of record. Ex 3 - b) 2. 63 N c) 1. 15 N d) 9. 98 N 24