L 02 Vectors and Scalars Outline 1 Physical

L 02. Vectors and Scalars Outline 1. Physical quantities - vectors and scalars; 2. Geometrical representation and properties of vectors; 3. Operations with vectors and concept of a resultant vector; 4. Vector components and unit vectors; 5. North-South-West-East vector notation; 6. Relative velocity; 7. Dot product. NU-CPS Physics 2014

1. Physical quantities - vectors and scalars Many physical quantities have both magnitude and direction: they are called vectors. • Examples: displacement, velocity, acceleration force, momentum. . . Other physical quantities have only magnitude: they are called scalars. • Examples: distance, speed, mass, energy. . . 2

Displacement and Distance • Displacement is the vector connecting a starting point A and some final point B B A • Distance is the length one would travel from point A to the final point B. Therefore distance is a scalar 3

2. Geometrical representation and properties of vectors • Arrows on a plane or space • To indicate a vector we use bold letters or an arrow on top of a letter • You are supposed to use arrows 4

Properties of Vectors 1. The opposite of a vector a is vector - a 2. It has the same length but opposite direction 3. Two vectors a and b are parallel if one is a positive multiple of the other: a = m b, m>0 Example: if a = 3 b, then a is parallel to b (if a = -2 b then a is anti-parallel to b) 5

3. Operations with vectors and concept of a resultant vector When we add two vectors, we get the resultant vector a + b, with the parallelogram rule: 6

Operations: Adding more vectors • We can add more vectors by pairing them appropriately 7

Operations: Vector Subtraction • Special case of vector addition q Add the negative of the subtracted vector • a – b = a + (– b) 8

4. Vector components and unit vectors • A component is a part or shadow along a given direction • It is useful to use rectangular components – projections of the vector along the xand y-axes 9

Components of a Vector, cont. • A vector in the component form 2 D: a=(ax, ay); 3 D: a=(ax, ay, az) • The x-component of a vector is the projection along the x-axis q ax = a cosθ • The y-component of a vector is the projection along the y-axis q ay = a sinθ 2 + a 2 )½ • The magnitude of vector : a = (ax y 10

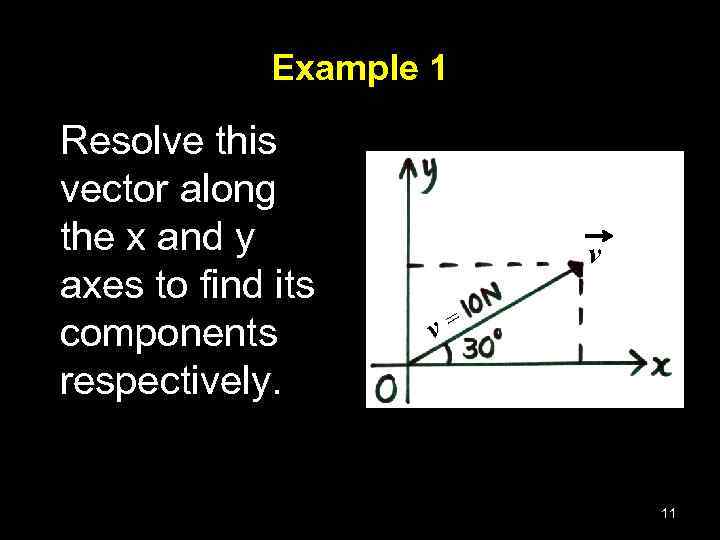Example 1 Resolve this vector along the x and y axes to find its components respectively. v v= 11

Example 2 A vector of 15. 0 N at 120º to the x-axis is added to the vector in Example 1. Find the x and y components of the resultant vector. u = 15. 0 N u v = 10. 0 N v 12

The Unit Vectors: i, j, k A unit vector has a magnitude of 1 i is the unit vector in the x-direction, j is in the y-direction and k is in the z-direction. 13

The Unit Vectors, Magnitude • Any vector a can be written as: q a=xi+yj+zk Example 3 : Given the two displacements Show that the magnitude of e is approximately 17 units where: 14

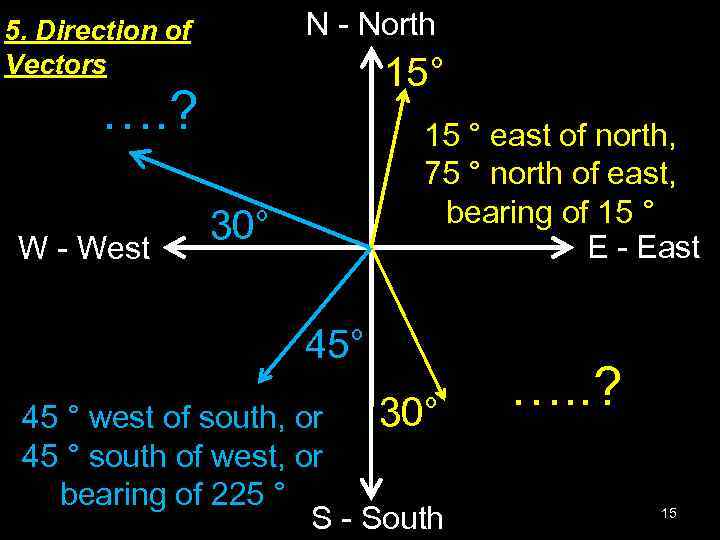N - North 5. Direction of Vectors 15° …. ? W - West 15 ° east of north, 75 ° north of east, bearing of 15 ° E - East 30° 45° 30° 45 ° west of south, or 45 ° south of west, or bearing of 225 ° S - South …. . ? 15

Example 4 Find the magnitude and direction of the electric field vector E with components 3 i – 4 j. Note: This vector could also be written in matrix form: 16

6. Relative velocity Suppose a cyclist (C) travels in a straight line relative to the earth (E) with velocity VCE. A pedestrian (P) is travelling relative to the earth (E) with velocity VPE. The relative velocity of the cyclist (C) with respect to the pedestrian (P) is given by : q VCP = VCE - VPE 17

Example 5 A boat is heading due north as it crosses a wide river with a velocity of 8. 0 km/h relative to water. The river has a uniform velocity of 6. 0 km/h due east. Determine the velocity (i. e. speed and direction) of the boat relative to an observer on the riverbank. 18

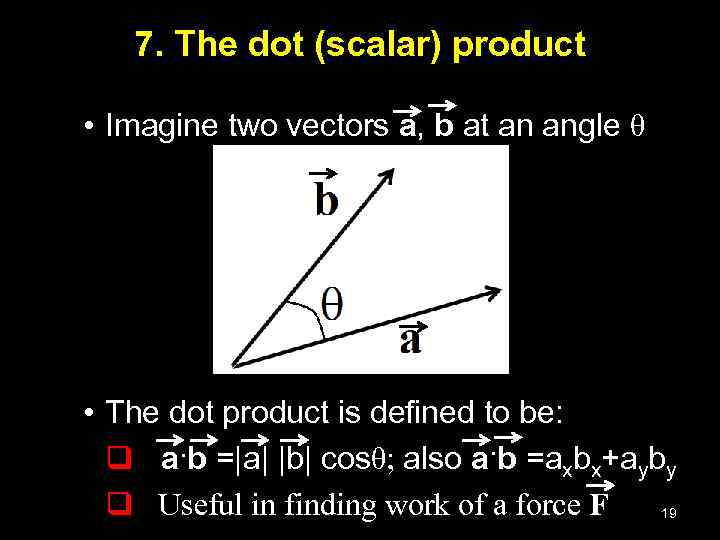7. The dot (scalar) product • Imagine two vectors a, b at an angle θ • The dot product is defined to be: q a·b =|a| |b| cosθ; also a·b =axbx+ayby q Useful in finding work of a force F 19

CHECK LIST • READING Serway’s Essentials of College Physics pages 41 -46 and 53 -55. Adams and Allday: 3. 3 pages 50 -51, 52 -53. Summary • Be able to give examples of physical quantities represented by vectors and scalars • Understand how to add and subtract vectors • Know what a resultant vector is • Know how to find the change in a vector quantity, calculate relative and resolve a vector into components • Understand how vectors can be represented in component form in a coordinate system • Be able to do calculations which demonstrate that you have understood the above concepts 20

Numerical Answers for Examples • • Ex 1 – Vx = 8. 7 N, Vy = 5 N Ex 2 – coordinates of resultant vector are (1. 16, 18. 0) Ex 3 – length is 16. 9 units, or approximately 17 units Unknown Directions – • Ex Yellow is 60° S of E, or 30 ° E of S, or bearing 150° (90+60) Blue is 30° N of W, or 60 ° W of N, or bearing 300° (270+30) 4 – Resultant vector E : magnitude 5 units, – Direction 53° S of E, or 37° E of S, or bearing 143° (90 + 53) 5 – velocity of boat relative to earth: magnitude 10 km/hr – Direction 53° N of E, or 37° E of N, or bearing 37° 21