Квантовые свойства света Равновесное тепловое излучение Энергия

Квантовые свойства света Равновесное тепловое излучение

Энергия, расходуемая светящимся телом на излучение, может пополняться из различных источников. Самым распространенным является свечение тел, обусловленное их нагреванием. Этот вид свечения называется тепловым излучением. Оно имеет место при любой температуре, однако при невысоких температурах излучаются лишь длинные (инфракрасные) ЭМВ. Окружим излучающее тело непроницаемой оболочкой с идеально отражающей поверхностью. Воздух из оболочки удалим. Отраженное оболочкой излучение, упав на тело, поглотится им частично или полностью.

Значит, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Если распределение энергии между телом и излучением остается неизменным для каждой длины волны, состояние системы «тело-излучение» будет равновесным. Единственный вид излучения, которое может находиться в равновесии с излучающими телами – тепловое. Все остальные виды тепловое излучения, объединяемые общим названием люминесценция, оказываются люминесценция неравновесными. Такая способность теплового излучения связана с тем, что его интенсивность возрастает с повышением температуры.

Если равновесие между телом и излучением нарушено, тело может излучать больше, чем поглощает. Тогда внутренняя энергия тела будет убывать, что приведет к понижению температуры. Это в свою очередь обусловит уменьшение количества излучаемой энергии. Температура будет понижаться до тех пор, пока количество излучаемой энергии не станет равно количеству поглощаемой. Если равновесие нарушится в другую сторону, температура будет возрастать до тех пор, пока снова не установится равновесие. Таким образом нарушение равновесия в системе «тело-излучение» вызывает возникновение процессов, восстанавливающих равновесие.

Иначе дело обстоит в случае люминисценции. Покажем это на примере хемолюминесценции (окисляющийся на воздухе фосфор светится за счет энергии, выделяемой при химических превращениях). Пока протекает химическая реакция, излучающее тело все дальше удаляется от своего первоначального состояния. Поглощение телом излучения не изменит направление реакции, а наоборот, приведет к более быстрому (вследствие нагревания) протеканию реакции в первоначальном направлении. Равновесие установится лишь когда будет израсходован весь запас реагирующих веществ, и свечение, обусловленное химическими процессами, заменится тепловым излучением. К равновесным состояниям и процессам применимы законы термодинамики и общие закономерности, вытекающие из них.

Испускательная и поглощательная способность тела. Закон Кирхгофа Для характеристики теплового излучения будем пользоваться величиной потока энергии, измеряемой в ваттах. Поток энергии, испускаемый единицей поверхности излучающего тела по все направлениям (в пределах телесного угла 2π), называют энергетической светимостью тела RЭ. rw – испускательная способность тела. Она сильно зависит от температуры тела, т. е. она – функция и частоты, и температуры. Соответственно, и энергетическая светимость является функцией температуры:

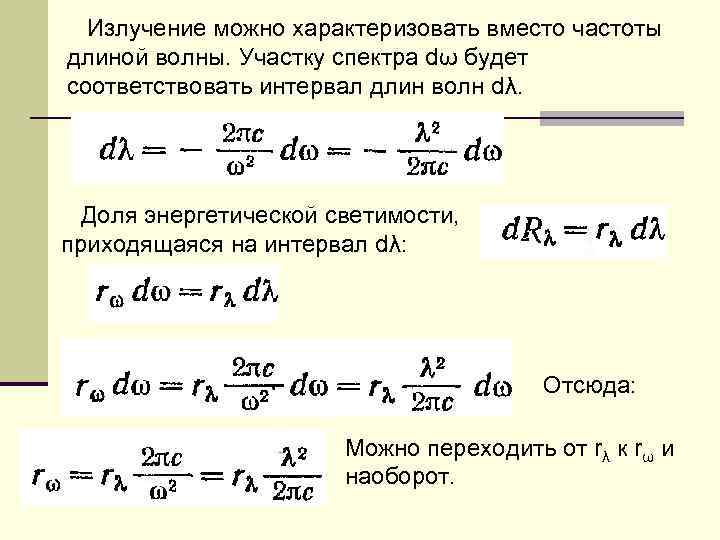Излучение можно характеризовать вместо частоты длиной волны. Участку спектра dω будет соответствовать интервал длин волн dλ. Доля энергетической светимости, приходящаяся на интервал dλ: Отсюда: Можно переходить от rλ к rω и наоборот.

Пусть на элементарную площадку поверхности падает поток лучистой энергии d. Фω, обусловленный электромагнитными волнами, частота которых заключена в интервале dω. Часть потока поглощается телом. Поглощательная способность тела: Поглощательная способность тела зависит от его температуры, т. е. она – функция и частоты, и температуры. По определению поглощательная способность не может быть больше единицы. Тело, полностью поглощающее упавшее на него излучение абсолютно черное: - серое тело

Между испускательной и поглощательной способностью любого тела имеется определенная связь. Пусть внутри замкнутой оболочки, поддерживаемой при постоянной температуре T, помещены несколько тел. Полость внутри оболочки эвакуирована, так что тела могут обмениваться энергией между собой и с оболочкой только путем испускания и поглощения электромагнитных волн. Через некоторое время эта система придет в состояние теплового равновесия – все тела примут одну и ту же температуру, равную температуре оболочки T.

Тело, обладающее большей испускательной способностью, теряет в единицу времени с единицы поверхности больше энергии, чем тело, обладающее меньшей rω. Поскольку температура тел не меняется, то тело, испускающее больше энергии, должно и поглощать больше. То есть чем больше испускательная, там больше и поглощательная способность тела. Отсюда для нескольких тел вытекает соотношение: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты (длины волны) и температуры Кирхгоф сформулировал следующий закон:

Испускательная и поглощательная способности тела, взятые отдельно, могут меняться чрезвычайно сильно при переходе от одного тела к другому, но их отношение – одинаковая величина для всех тел. Для абсолютно черного тела. Тогда для него rω = f(ω, T). Значит, универсальная функция Кирхгофа – это испускательная способность абсолютно черного тела. Абсолютно черных тел в природе не существует. Сажа или платиновая чернь имеют поглощательную способность, близкую к единице лишь в ограниченном интервале частот. В инфракрасной области их поглощательная способность значительно меньше единицы.

Можно создать устройство сколь угодно близкое по своим свойствам к абсолютно черному телу, например – почти замкнутую полость с небольшим отверстием. Излучение, проникшее через отверстие, прежде чем выйти обратно, претерпевает многократные отражения. При каждом отражении часть энергии поглощается, в результате почти все излучение любой частоты поглощается полостью. По той же причине внутренность комнаты в яркий солнечный день при рассматривании издали в открытое окно кажется темной. Если стенки полости поддерживаются при некоторой температуре Т, то из отверстия выходит излучение, близкое по спектральному составу к излучению абсолютно черного тела при той же температуре.

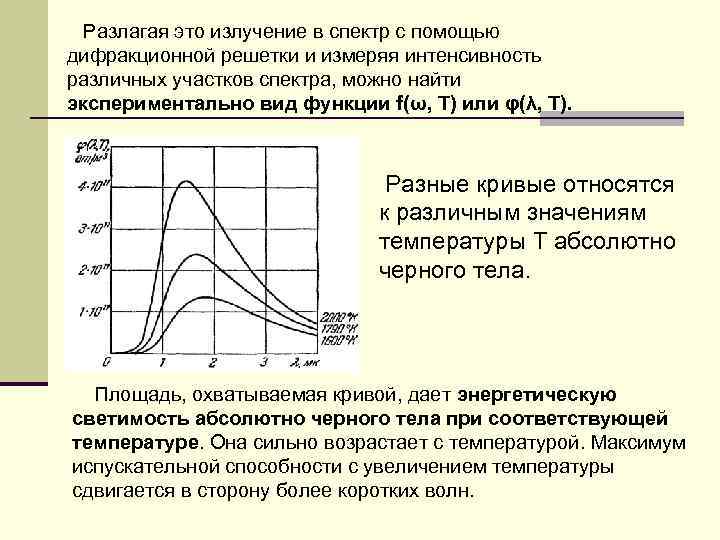Разлагая это излучение в спектр с помощью дифракционной решетки и измеряя интенсивность различных участков спектра, можно найти экспериментально вид функции f(ω, T) или φ(λ, T). Разные кривые относятся к различным значениям температуры Т абсолютно черного тела. Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре. Она сильно возрастает с температурой. Максимум испускательной способности с увеличением температуры сдвигается в сторону более коротких волн.

Закон Стефана-Больцмана и закон Вина Теоретическое объяснение излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к понятию квантов энергии. Долгое время попытки получить вид функции f(ω, T) не давали общего решения задачи. Австрийский физик Йозеф Стефан (1879 г. ), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость любого тела пропорциональна четвертой степени абсолютной температуры Однако последующие более точные измерения показали ошибочность его выводов.

В 1884 г. ассистент Стефана Людвиг Больцман, исходя из термодинамических соображений, получил значение Здесь σ – постоянная величина, Т – абсолютная температура. Таким образом, заключение, к которому Стефан пришел для нечерных тел (он не проводил опыты с абсолютно черными) оказались справедливыми лишь для черных тел. Соотношение между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана-Больцмана. Константу σ называют постоянной Стефана-Больцмана. Ее экспериментальное значение равно:

Вильгельм Вин, немецкий физик, в 1893 г. воспользовался также электромагнитной теорией и показал, что функция спектрального распределения должны иметь вид: Здесь F – неизвестная функция отношения частоты к температуре. Согласно формуле получается выражение: где - неизвестная функция произведения. Это соотношение позволяет установить зависимость между длиной волны, на которую приходится максимум функции φ(λT), и температурой.

Продифференцируем его по длине волны: Выражение в квадратных скобках представляет собой некоторую функцию ψ(λT). При длине волны λm, соответствующей максимуму функции φ(λ, T), выражение для dφ/dλ должно обращаться в ноль: Поскольку λm не равно бесконечности, должно выполняться условие: Решение этого уравнения относительно неизвестного произведения λm. T дает для неизвестного некоторое число, которое обозначим буквой b. Таким образом, получается соотношение, называемое законом смещения Вина: Экспериментальное значение константы b равно:

Формула Рэлея-Джинса Джон Стретт (лорд Рэлей) и Джеймс Джинс, британские физики, в 1905 г. сделали попытку определить функцию f(ω, T), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебания приходится в среднем энергия, равная двум половинкам k. T – одна половинка на электрическую, вторая – на магнитную энергию волны. Рассмотрим излучение, находящееся в равновесии в веществом. Представим себе эвакуированную полость, стенки которой поддерживаются при постоянной температуре T. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью u=u(T).

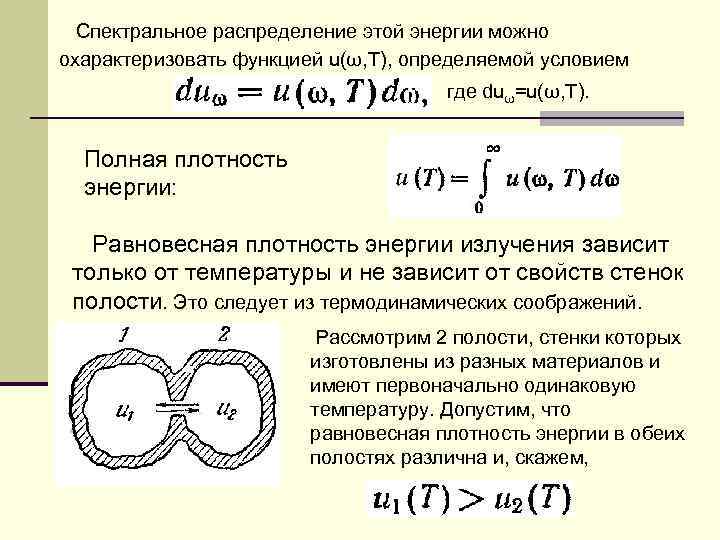Спектральное распределение этой энергии можно охарактеризовать функцией u(ω, T), определяемой условием где duω=u(ω, T). Полная плотность энергии: Равновесная плотность энергии излучения зависит только от температуры и не зависит от свойств стенок полости. Это следует из термодинамических соображений. Рассмотрим 2 полости, стенки которых изготовлены из разных материалов и имеют первоначально одинаковую температуру. Допустим, что равновесная плотность энергии в обеих полостях различна и, скажем,

Соединим полости небольшим отверстием, что вызовет теплообмен через излучение. Поток энергии во вторую полость будет больше, и ее стенки поглощают больше, чем излучают, значит, температура повышается. Стенки первой полости станут поглощать энергии меньше, чем излучать, значит, температура снизится. Однако 2 тела с первоначально одинаковой температурой не могут вследствие теплообмена друг с другом приобрести различные температуры – это запрещено вторым началом термодинамики. Поэтому наше допущение о неодинаковости u 1 и u 2 должно быть признано неправомерным. Вывод о равенстве u 1(Т) и u 2(Т) распространяется на каждую спектральную составляющую u(ω, T).

Равновесная плотность энергии излучения U связана с энергетической светимостью абсолютно черного тела Rэ* простым соотношением, которое мы сейчас выведем. В случае плоской волны плотность потока энергии – это произведение плотности энергии u и скорости волны c: I=cu. Поток энергии распределен равномерно в пределах телесного угла 4π. В пределах телесного угла dΩ будет заключен поток энергии с плотностью Если взять элементарную площадку ∆S, она посылает в пределах телесного угла dΩ=sin d dφ поток энергии:

Площадка ∆S посылает по всем направлениям внутрь телесного угла 2π поток энергии: Но поток должен быть таким же, как если бы его излучали абсолютно черные стенки. По определению он равен Rэ* ∆S. Значит, Это соотношение должно выполняться для каждой спектральной составляющей излучения. Отсюда

Рэлей и Джинс исходили из того, что равновесное излучение в полости представляет собой систему стоячих волн. Такое представление оправдывается тем, что замена поглощающих стенок полости идеально отражающими не изменяет плотности энергии равновесного излучения. Исходя из закона равнораспределения энергии по степеням свободы, Рэлей и Джинс приписали каждому колебанию энергию, равную k. T: или Перейдя от u(ω, T) к f(ω, T), получим

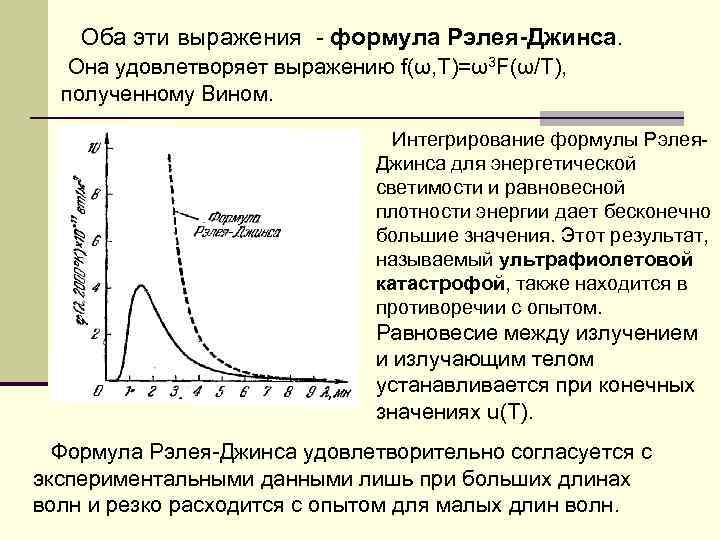Оба эти выражения - формула Рэлея-Джинса. Она удовлетворяет выражению f(ω, T)=ω3 F(ω/T), полученному Вином. Интегрирование формулы Рэлея. Джинса для энергетической светимости и равновесной плотности энергии дает бесконечно большие значения. Этот результат, называемый ультрафиолетовой катастрофой, также находится в противоречии с опытом. Равновесие между излучением и излучающим телом устанавливается при конечных значениях u(T). Формула Рэлея-Джинса удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн и резко расходится с опытом для малых длин волн.

Формула Планка Расхождение формулы Рэлея-Джинса с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической статистической физики и электродинамики. В 1900 г. Макс Планк, немецкий физик, нашел вид функции f(ω, T), в точности соответствующий опытным данным. Для этого он сделал предположение, совершенно чуждое классическим представлениям – что электромагнитное излучение испускается в виде отдельных порций энергии ε (квантов), величина которых пропорциональна частоте излучения: ε=ħω.

Коэффициент пропорциональности получил впоследствии название постоянной Планка. Из опыта она равна ħ=1, 054· 10 -34 Дж·с. На научном жаргоне эту величину обычно называют «постоянная с планкой» , используется также соотношение ħ=h/2π Если излучение испускается порциями ħω, то его энергия εп должна быть кратной этой величине: εп =nħω (n=0, 1, 2. . ). Для средней энергии излучения частоты ω можно получить выражение При ħ->0 эта формула переходит в классическое выражение ε=k. T. В этом можно убедиться, положив Это будет выполняться тем точнее, чем меньше ħ.

Таким образом, если бы энергия могла принимать непрерывный ряд значений, ее среднее значение было бы равно k. T. Заменив в формуле Рэлея-Джинса k. T выражением для εср, получим формулу, найденную Планком: Эта формула точно согласуется с экспериментальными данными во всем интервале частот от 0 до ∞. Она удовлетворяет критерию Вина: При условии, что (малые частоты или большие длины волны), можно положить равным приближенно , в результате формула Планка перейдет в формулу Рэлея-Джинса.

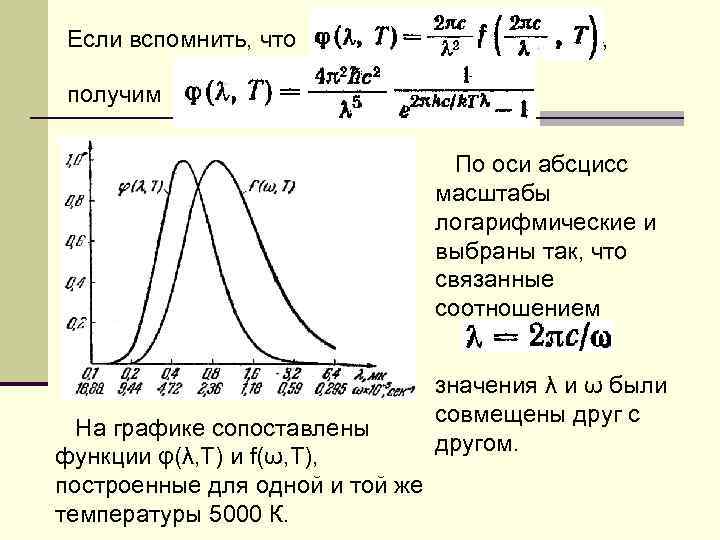Если вспомнить, что , получим По оси абсцисс масштабы логарифмические и выбраны так, что связанные соотношением На графике сопоставлены функции φ(λ, T) и f(ω, T), построенные для одной и той же температуры 5000 К. значения λ и ω были совмещены друг с другом.

Из рисунка видно, что частота ωm, соответствующая максимуму f(ω, T), не совпадает с 2πc/λm, где λm – длина волны, отвечающая максимуму φ(λ, T). Для энергетической светимости абсолютно черного тела получается выражение Введем вместо ω безразмерную переменную x=ħω/k. T. Тогда для энергетической светимости получим: Интеграл в этой формуле можно вычислить. Он равен π4/15 ≈ 6, 5. Подставив это, придем к закону Стефана-Больцмана: Подставляя в эту формулу численные значения k, с и ħ, получим для постоянной Стефана-Больцмана значение, очень хорошо согласующееся с экспериментальным значением.

Найдем постоянную в законе смещения Вина. Для этого продифференцируем функцию φ(λ, Т) по λ и приравняем получившееся выражение нулю: Значение λm, при котором функция достигает максимума, обращает в ноль выражение, стоящее в числителе в квадратных скобках. Пусть . Получим уравнение xex-5(ex-1)=0. Решая, получим x=4, 965 и. Подстановка значений ħ, c и k дает величину b, совпадающую с экспериментальным значением. То есть формула Планка исчерпывающе описывает равновесное тепловое излучение.

Тормозное рентгеновское излучение Квантовая природа излучения подтверждается также существованием коротковолновой границы тормозного рентгеновского спектра. Рентгеновские лучи возникают при бомбардировке быстрыми электронами твердых мишеней. Существуют 2 вида рентгеновских трубок – ионные (в них при низком давлении поддерживается тлеющий разряд) и электронные, где свободные электроны возникают вследствие электронной эмиссии с нагреваемого током катода. Электронные трубки гораздо устойчивее и проще в эксплуатации.

Если между катодом и мишенью (антикатодом) приложено напряжение U, электроны разгонятся до энергии e. U. Попадая в вещество антикатода, они тормозятся и становятся источником ЭМВ. Интенсивность излучения равна: Заметное излучение может наблюдаться лишь при резком торможении быстрых электронов. Чем меньше длина волны, тем меньше электроны поглощаются веществом. При достаточно большой скорости электронов, кроме тормозного излучения (обусловленного торможением электронов) возбуждается также характеристическое излучение (вызванное возбуждением внутренних электронных оболочек антикатода). Но сейчас мы рассматриваем только тормозное излучение, а о характеристическом будет рассказано в курсе атомной физики.

Согласно классической электродинамике, при торможении электрона должны возникать волны всех длин – от нуля до бесконечности. Длина волны, на которую приходится максимум интенсивности излучения, должна уменьшаться по мере увеличения скорости электронов, т. е. напряжения на трубке U. На рисунке даны экспериментальные кривые распределения интенсивности тормозного рентгеновского излучения по длинам волн для разных U. Но имеется отступление от требований классической электродинамики. Кривые распределения интенсивности не идут к началу координат, а обрываются при конечных значениях длины волны λmin.

Экспериментально установлено, что коротковолновая граница тормозного рентгеновского спектра λmin связана с ускоряющим напряжением U соотношением: Здесь λ выражена в ангстремах, а U – в вольтах. Существование коротковолновой границы непосредственно вытекает из квантовой природы излучения. Если излучение возникает за счет энергии, теряемой электроном при торможении, то величина кванта ħω не может превысить энергию электрона e. U: Значит, частота излучения не должна превысить значения ωmax=e. U/ħ, а значит, длина волны не может быть меньше значения (а это совпадает с экспериментом) Из всех методов определения постоянной Планка измерение коротковолновой границы тормозного рентгеновского спектра считается самым точным.

Фотоэффект Фотоэлектрическим эффектом или фотоэффектом называется испускание электронов веществом под действием света. Это явление было открыто в 1887 г. немецким физиком Генрихом Герцем. В 1889 русский физик Александр Столетов исследовал фотоэффект и выявил следующие закономерности: 1) испускаемые под действием света заряды имеют отрицательный знак; 2) наибольшее действие оказывают ультрафиолетовые лучи; 3) величина испущенного телом заряда пропорциональна поглощенной им световой энергии.

В 1898 г. английский физик Джозеф Томсон и немецкий физик Филипп Ленард, измерив удельный заряд испускаемых под действием света частиц, установили, что эти частицы являются электронами. На рисунке показана схема установки для исследования фотоэффекта. Свет проникает через кварцевое окошко в эвакуированный баллон и освещает катод, изготовленный из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду. В результате в цепи прибора течет фототок, измеряемый гальванометром. Напряжение между анодом и катодом можно изменять с помощью потенциометра.

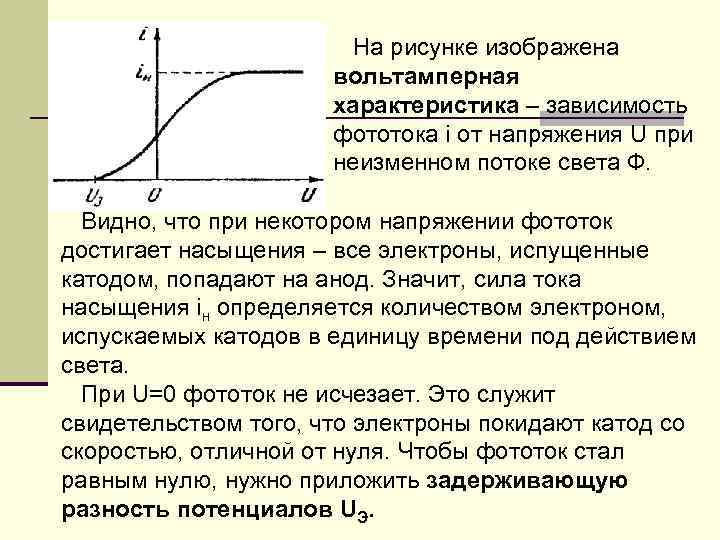На рисунке изображена вольтамперная характеристика – зависимость фототока i от напряжения U при неизменном потоке света Ф. Видно, что при некотором напряжении фототок достигает насыщения – все электроны, испущенные катодом, попадают на анод. Значит, сила тока насыщения iн определяется количеством электроном, испускаемых катодов в единицу времени под действием света. При U=0 фототок не исчезает. Это служит свидетельством того, что электроны покидают катод со скоростью, отличной от нуля. Чтобы фототок стал равным нулю, нужно приложить задерживающую разность потенциалов UЭ.

При таком напряжении ни одному из электронов, даже обладающему при вылете из катода наибольшим значением скорости, не удается преодолеть задерживающее поле и достигнуть анода. Поэтому (где m – масса электрона). Измерив задерживающее напряжение UЭ, можно определить максимальное значение скорости фотоэлектронов. При неизменном спектральном составе падающего на катод света сила тока насыщения строго пропорциональна световому потоку Ф: Это утверждение – закон Столетова. Задерживающее напряжение от интенсивности света не зависит.

Для того, чтобы электроны могли покинуть катод под действием света, необходимо выполнение условия: Частота или длина волны λ 0 называется красной границей фотоэффекта. Ее можно найти, определив частоту, при которой задерживающее напряжение обращается в ноль. Законы фотоэффекта противоречат представлениям волновой теории света. По этим представлениям под действием световой ЭМВ электроны вещества совершают вынужденные колебания, и связь их с веществом при интенсивных колебаниях может быть нарушена так, что электроны будут вылетать наружу со скоростью, зависящей от интенсивности света. В действительности такой зависимости нет – скорость электронов зависит только от частоты падающего света.

Альберт Эйнштейн в 1905 г. показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет поглощается такими же порциями ħω (квантами), как и испускается. Энергия, полученная электроном, доставляется ему в виде кванта ħω, который усваивается целиком. Часть этой энергии, равная работе выхода eφ, затрачивается на то, чтобы электрон покинул тело. Часть может быть затрачена на случайные столкновения в веществе. Остаток образует кинетическую энергию Wħ электрона, покинувшего вещество. Она будет максимальна, если энергия на столкновения в веществе не тратится. Тогда следующее соотношение называется формулой Эйнштейна:

Кроме рассмотренного нами внешнего фотоэффекта, называемого обычно просто фотоэффектом, существует также внутренний фотоэффект, наблюдаемый в диэлектриках и полупроводниках. Он заключается в обусловленном действием света перераспределении электронов по энергетическим уровням. В результате появляется дополнительная пара носителей заряда - электрон и дырка, а электропроводность вещества возрастает. Если в веществе есть примеси, под действием света электроны могут переходить из валентной зоны на уровни примеси или с примесных уровней в зону проводимости. В первом случае возникает дырочная, во втором – электронная проводимость. Количество носителей заряда пропорционально падающему световому потоку. На внутреннем фотоэффекте основано действие фотосопротивлений, которые применяются в фотометрии.

Принцип действия p-n перехода: в процессе контакта из области с полупроводником n-типа в область с полупроводником p-типа проходят электроны, которые затем рекомбинируют с дырками. В области p-n перехода или на границе металла с полупроводником может наблюдаться вентильный фотоэффект. Он заключается в возникновении под действием света электродвижущей силы. На рисунке показан ход потенциальной энергии электронов и дырок. Неосновные для данной области носители проходят через переход, в p-области накапливается избыточный положительный, а в области – отрицательный заряд. Это приводит к возникновению приложенного к переходу напряжения, которое представляет собой фотоэлектродвижущую силу.