Квантовая Теория_2012.ppt
- Количество слайдов: 101
 Квантовая Теория Курс 2012
Квантовая Теория Курс 2012
 Ауд 193 а • Запрягаев Сергей Александрович • 1 лекция – 1 час практики в неделю
Ауд 193 а • Запрягаев Сергей Александрович • 1 лекция – 1 час практики в неделю
 Литература • А. С. Давыдов. Квантовая механика • Д. И. Блохинцев. Квантовая механика • Флюгге З. Задачи по квантовой механике, том 1 (Мир, 1974) • Флюгге З. Задачи по квантовой механике, том 2 (Мир, 1974
Литература • А. С. Давыдов. Квантовая механика • Д. И. Блохинцев. Квантовая механика • Флюгге З. Задачи по квантовой механике, том 1 (Мир, 1974) • Флюгге З. Задачи по квантовой механике, том 2 (Мир, 1974
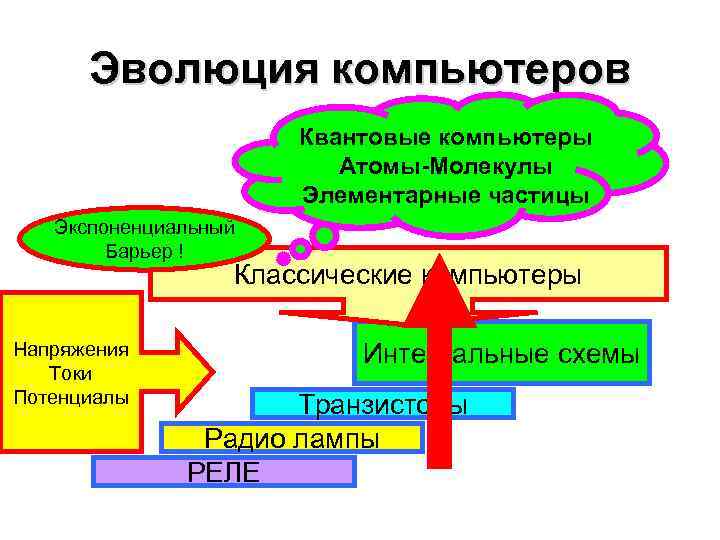 Эволюция компьютеров Квантовые компьютеры Атомы-Молекулы Элементарные частицы Экспоненциальный Барьер ! Классические компьютеры Напряжения Токи Потенциалы Интегральные схемы Транзисторы Радио лампы РЕЛЕ
Эволюция компьютеров Квантовые компьютеры Атомы-Молекулы Элементарные частицы Экспоненциальный Барьер ! Классические компьютеры Напряжения Токи Потенциалы Интегральные схемы Транзисторы Радио лампы РЕЛЕ
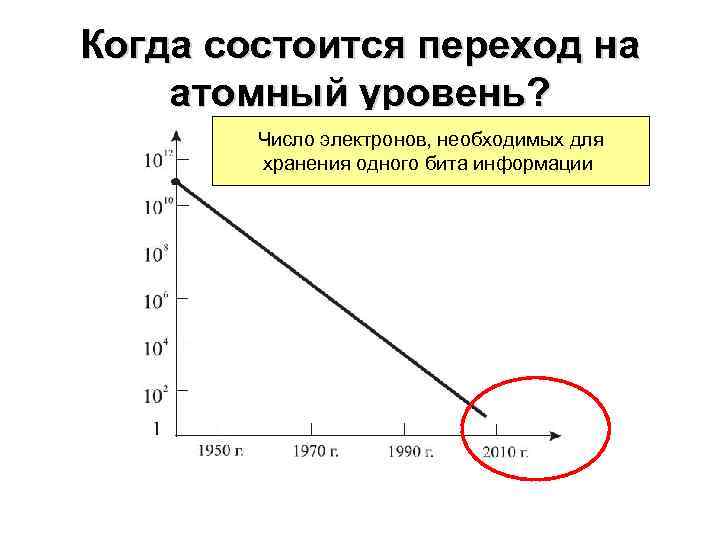 Когда состоится переход на атомный уровень? Число электронов, необходимых для хранения одного бита информации
Когда состоится переход на атомный уровень? Число электронов, необходимых для хранения одного бита информации
 Модель Томсона
Модель Томсона
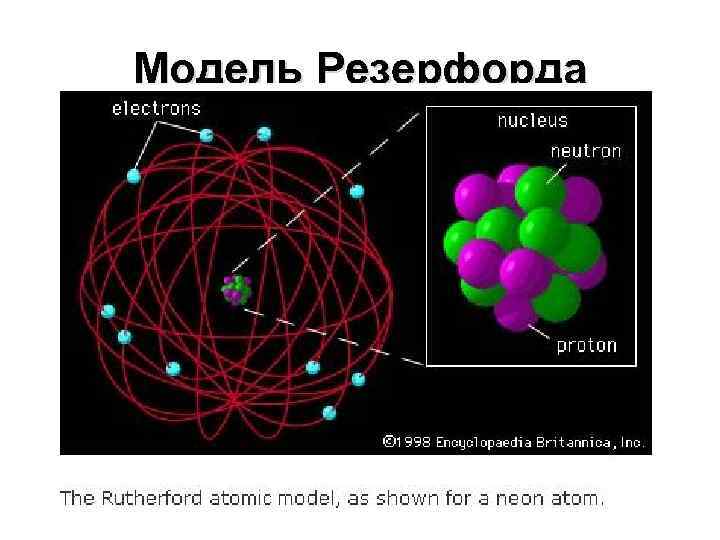 Модель Резерфорда
Модель Резерфорда
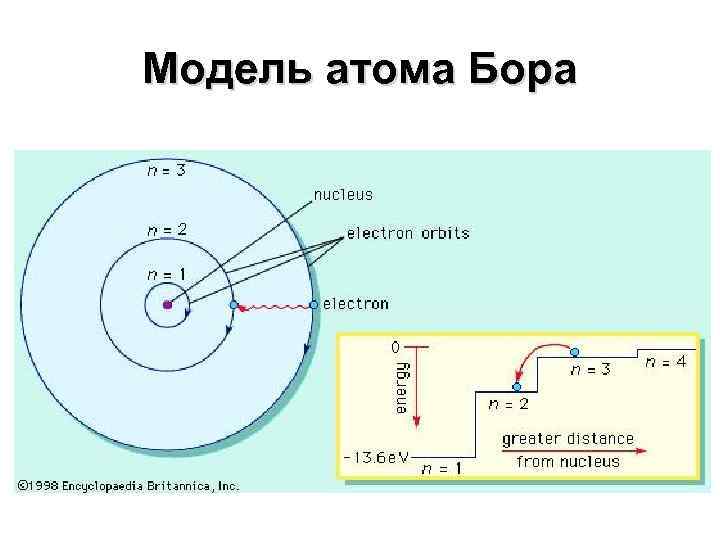 Модель атома Бора
Модель атома Бора
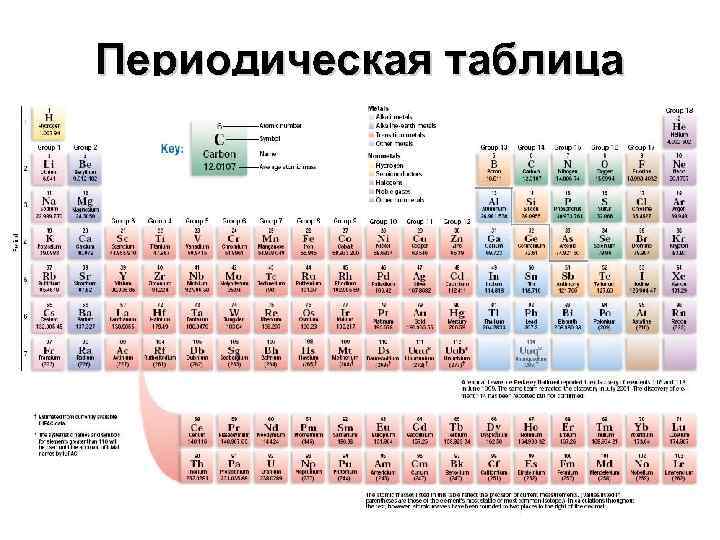 Периодическая таблица
Периодическая таблица
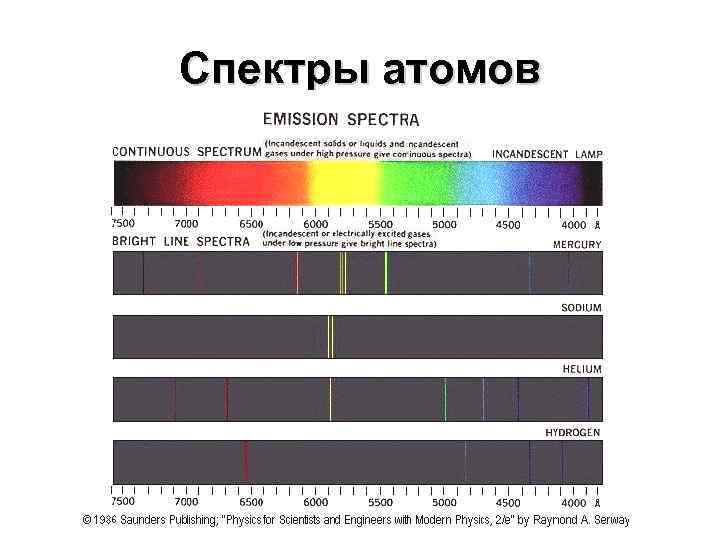 Спектры атомов
Спектры атомов
 Рубиновый лазер
Рубиновый лазер
 CD / DVD диски
CD / DVD диски
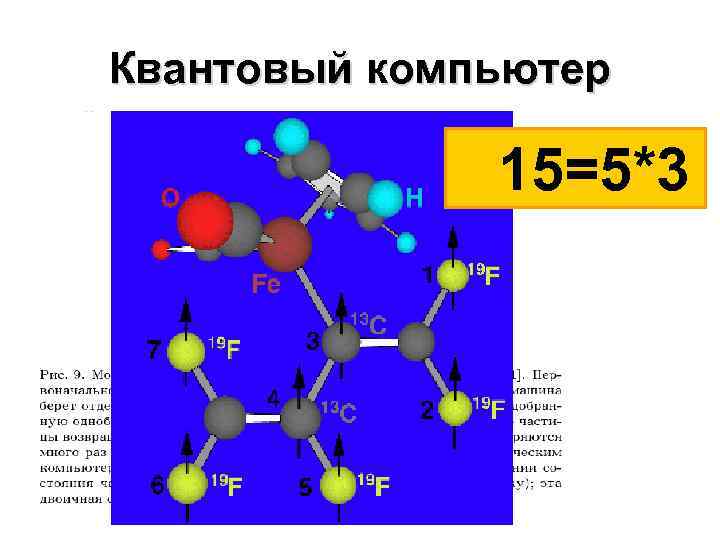 Квантовый компьютер 15=5*3
Квантовый компьютер 15=5*3
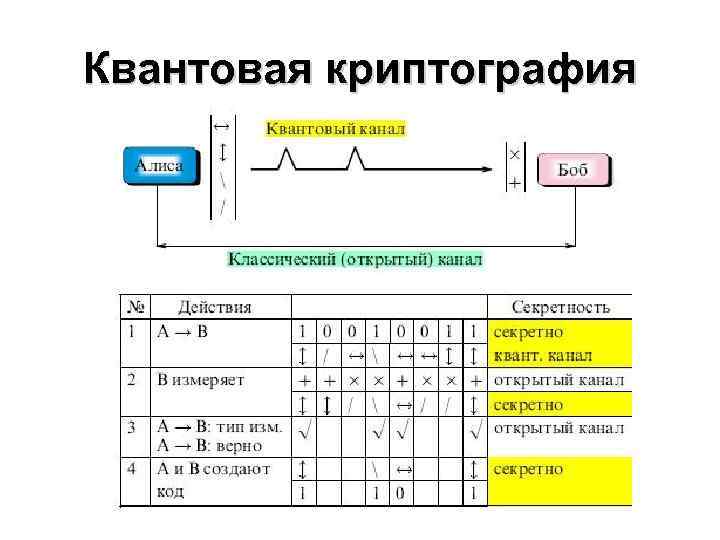 Квантовая криптография
Квантовая криптография
 Телепортация Город В Город А
Телепортация Город В Город А
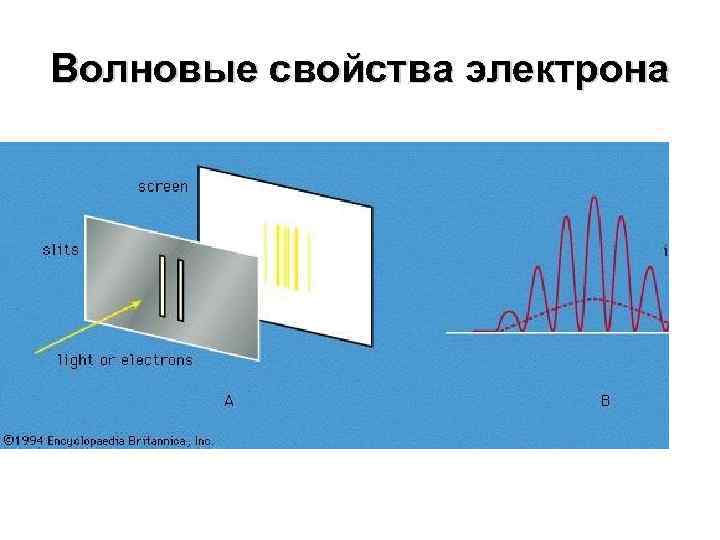 Волновые свойства электрона
Волновые свойства электрона
 Волновые свойства • Электромагнитное поле • Векторный потенциал • Волна де Бройля
Волновые свойства • Электромагнитное поле • Векторный потенциал • Волна де Бройля
 § Алгебра операторов • y=F(x) ; y = F x; • Оператор == математическая операция • Символическое обозначение • Равенство операторов • Число – частный случай оператора • Линейность операторов
§ Алгебра операторов • y=F(x) ; y = F x; • Оператор == математическая операция • Символическое обозначение • Равенство операторов • Число – частный случай оператора • Линейность операторов
 § Алгебра операторов … • • Сложение (вычитание) операторов Произведение операторов !! Коммутатор двух операторов Целая положительная степень Обратный оператор Функция от оператора Эрмитовский оператор
§ Алгебра операторов … • • Сложение (вычитание) операторов Произведение операторов !! Коммутатор двух операторов Целая положительная степень Обратный оператор Функция от оператора Эрмитовский оператор
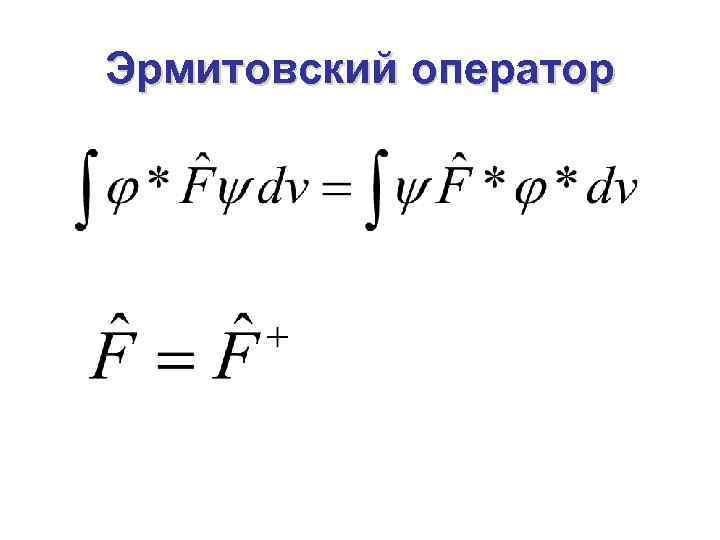 Эрмитовский оператор
Эрмитовский оператор
 § Собственные функции оператора • Собственные функции и собственные значения оператора Оператор Собственное значение Собственная функция
§ Собственные функции оператора • Собственные функции и собственные значения оператора Оператор Собственное значение Собственная функция
 § Спектр оператора • Спектр оператора - дискретный, непрерывный, смешанный Дискретный спектр f 1 , f 2 , f 3 , … f n … 1, 2, 3 …, n Непрерывный спектр
§ Спектр оператора • Спектр оператора - дискретный, непрерывный, смешанный Дискретный спектр f 1 , f 2 , f 3 , … f n … 1, 2, 3 …, n Непрерывный спектр
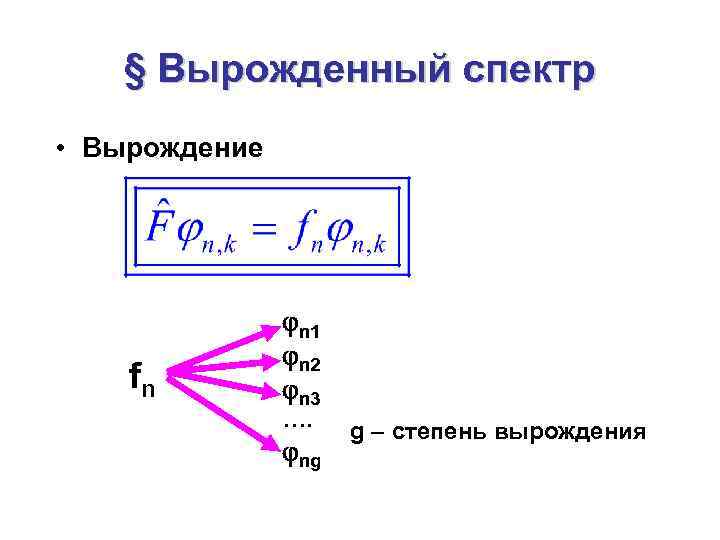 § Вырожденный спектр • Вырождение fn n 1 n 2 n 3 …. ng g – степень вырождения
§ Вырожденный спектр • Вырождение fn n 1 n 2 n 3 …. ng g – степень вырождения
 Теоремы для эрмитовских операторов • Теорема 1. Собственные функции образуют полный набор. • Теорема 2. Собственные значения – действительные числа!
Теоремы для эрмитовских операторов • Теорема 1. Собственные функции образуют полный набор. • Теорема 2. Собственные значения – действительные числа!
 Теоремы для эрмитовских операторов … • Теорема 3. Собственные функции коммутирующих линейных эрмитовских операторов одинаковы • Теорема 4. Собственные функции эрмитовских операторов – ортонормированы
Теоремы для эрмитовских операторов … • Теорема 3. Собственные функции коммутирующих линейных эрмитовских операторов одинаковы • Теорема 4. Собственные функции эрмитовских операторов – ортонормированы
 Постулаты квантовой теории • Состояние • Принцип суперпозиции состояний • Волновая функция (статистическая интерпретация волновой функции) • Физическая величина – оператор • Уравнение Шредингера (стандартные условия) • Постулат об измерении
Постулаты квантовой теории • Состояние • Принцип суперпозиции состояний • Волновая функция (статистическая интерпретация волновой функции) • Физическая величина – оператор • Уравнение Шредингера (стандартные условия) • Постулат об измерении
 Волновая функция • Статистическая интерпретация • Одномерное уравнение Шредингера
Волновая функция • Статистическая интерпретация • Одномерное уравнение Шредингера
 Статистическая интерпретация
Статистическая интерпретация
 Ортонормировка
Ортонормировка
 Оператор импульса в координатном представлении
Оператор импульса в координатном представлении
 операторы содержащие p
операторы содержащие p
 Уравнение Шредингера
Уравнение Шредингера
 Стационарное уравнение Шредингера
Стационарное уравнение Шредингера
 Одномерное уравнение Шредингера Волновая функция: • Непрерывна • Ограничена • Однозначна
Одномерное уравнение Шредингера Волновая функция: • Непрерывна • Ограничена • Однозначна
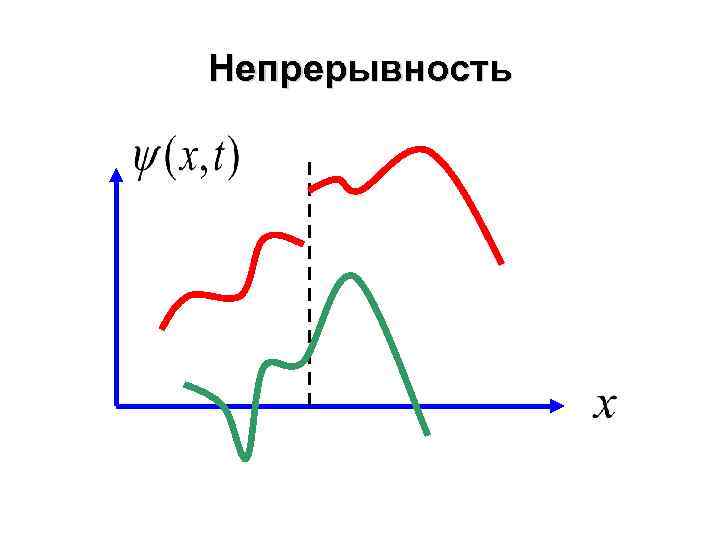 Непрерывность
Непрерывность
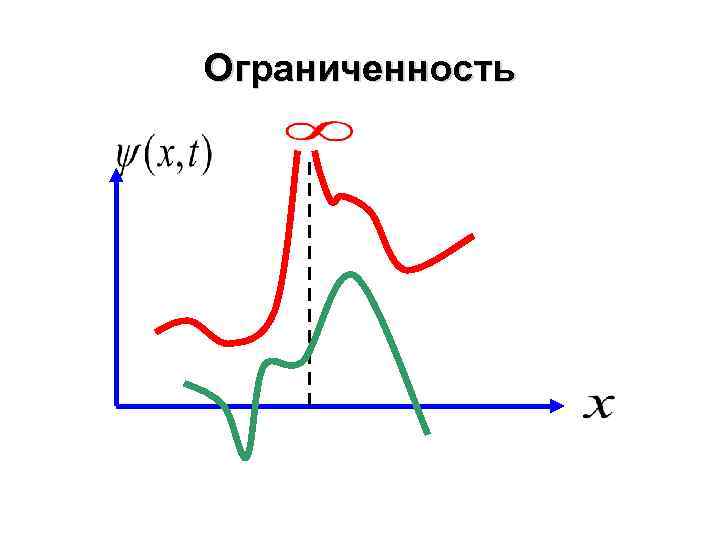 Ограниченность
Ограниченность
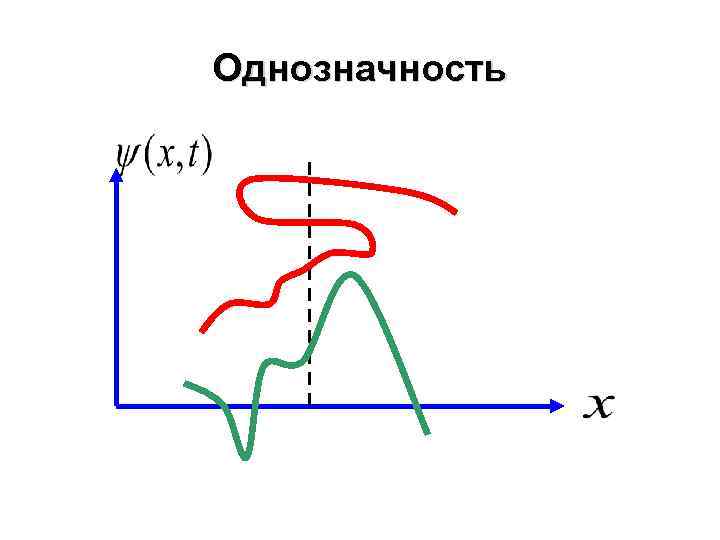 Однозначность
Однозначность
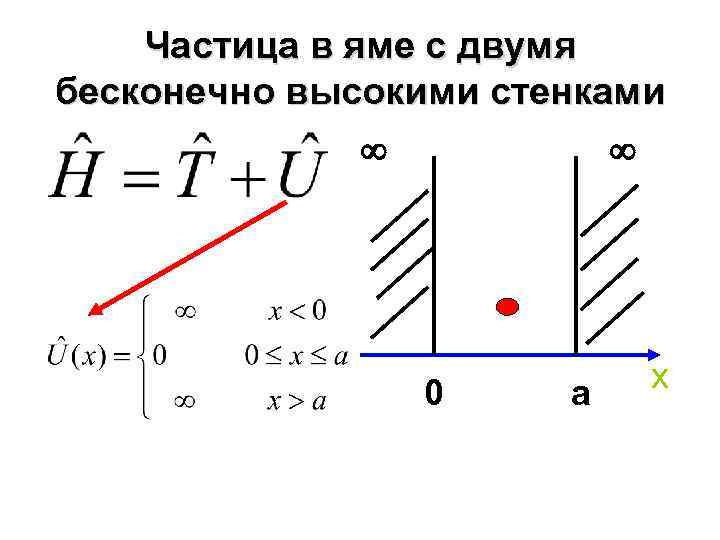 Частица в яме с двумя бесконечно высокими стенками 0 a x
Частица в яме с двумя бесконечно высокими стенками 0 a x
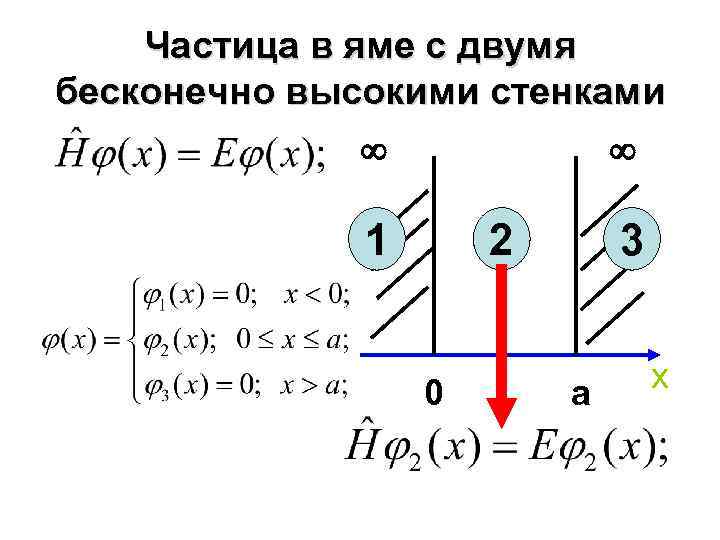 Частица в яме с двумя бесконечно высокими стенками 1 2 0 3 a x
Частица в яме с двумя бесконечно высокими стенками 1 2 0 3 a x
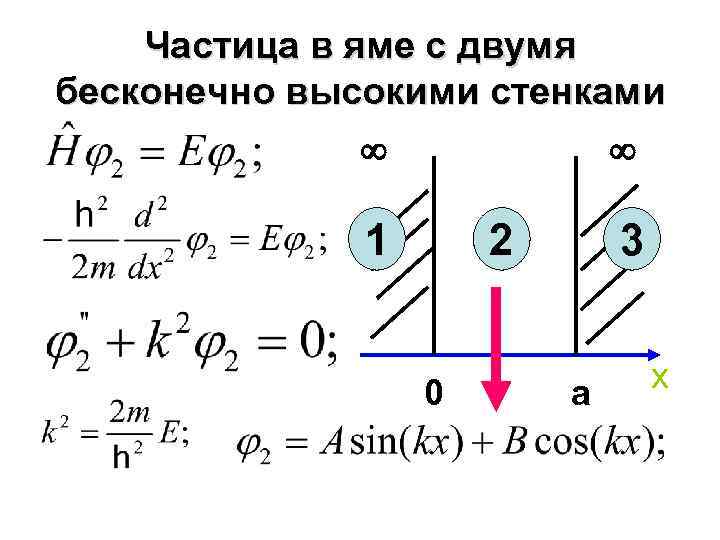 Частица в яме с двумя бесконечно высокими стенками 1 2 0 3 a x
Частица в яме с двумя бесконечно высокими стенками 1 2 0 3 a x
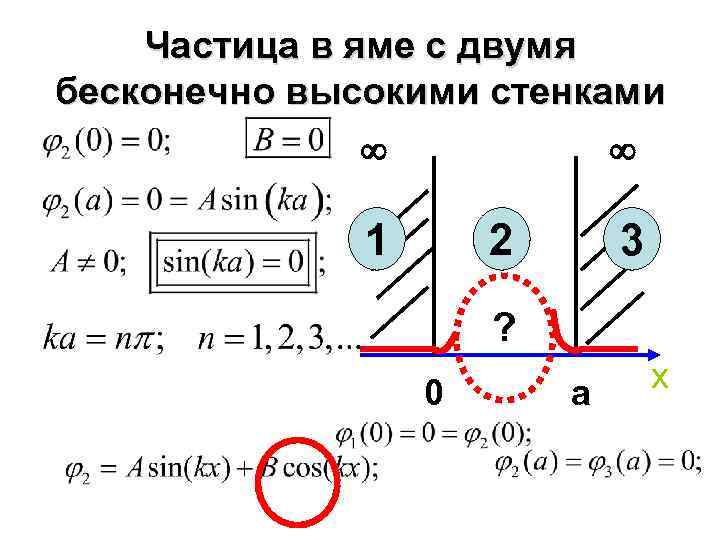 Частица в яме с двумя бесконечно высокими стенками 1 2 3 ? 0 a x
Частица в яме с двумя бесконечно высокими стенками 1 2 3 ? 0 a x
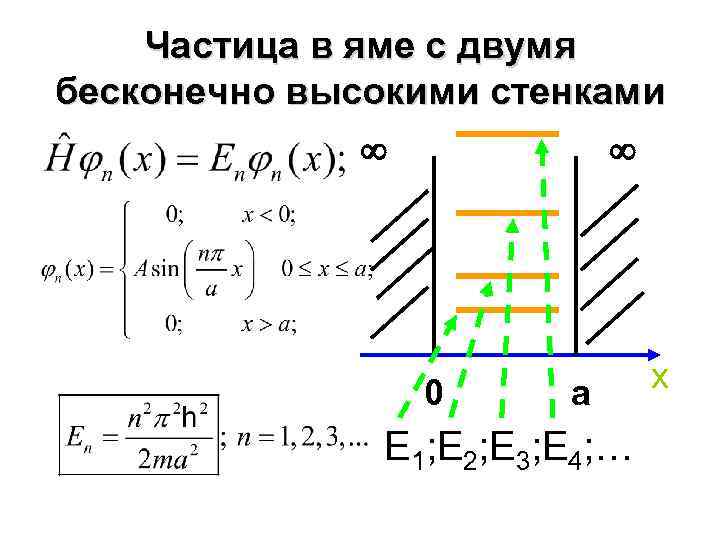 Частица в яме с двумя бесконечно высокими стенками 0 a E 1; E 2; E 3; E 4; … x
Частица в яме с двумя бесконечно высокими стенками 0 a E 1; E 2; E 3; E 4; … x
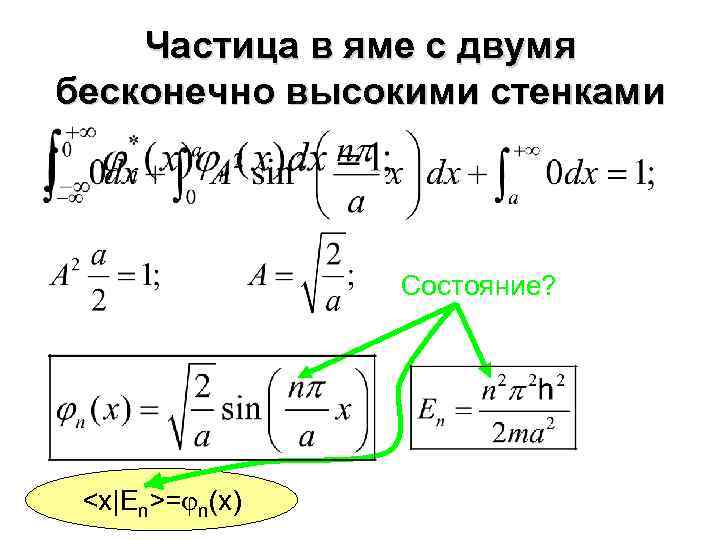 Частица в яме с двумя бесконечно высокими стенками Состояние?
Частица в яме с двумя бесконечно высокими стенками Состояние?
 Частица в яме с двумя бесконечно высокими стенками n=1 | n=1|2 | n=2|2 n=2
Частица в яме с двумя бесконечно высокими стенками n=1 | n=1|2 | n=2|2 n=2
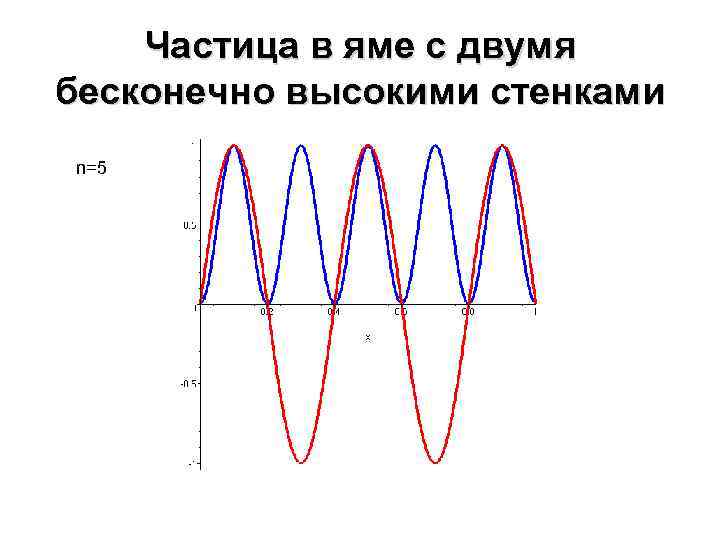 Частица в яме с двумя бесконечно высокими стенками n=5
Частица в яме с двумя бесконечно высокими стенками n=5
 Предельный переход от квантовой механики к классической Сравнить
Предельный переход от квантовой механики к классической Сравнить
 Мячик в поле тяжести z 0 (0)=0
Мячик в поле тяжести z 0 (0)=0
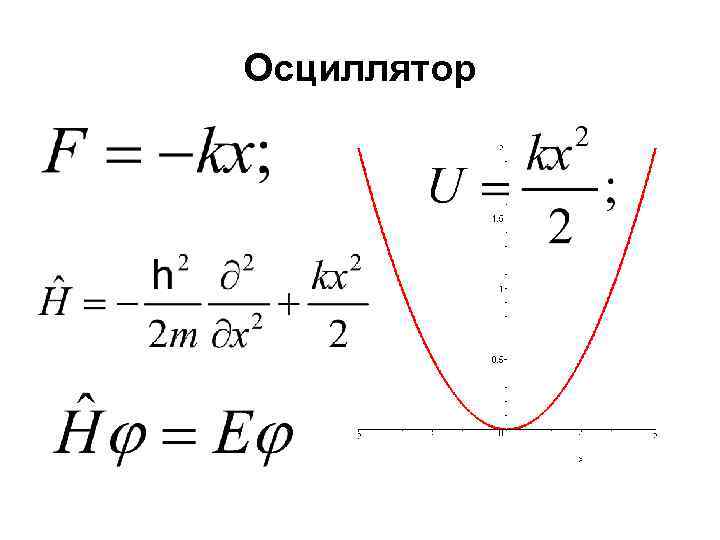 Осциллятор
Осциллятор
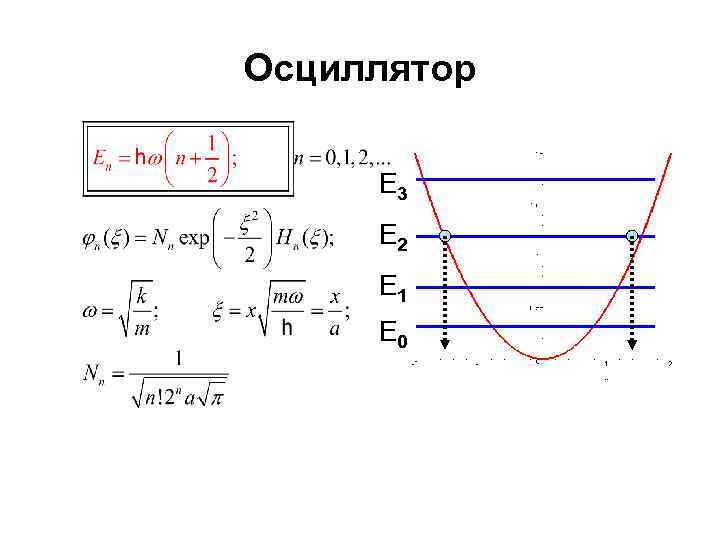 Осциллятор E 3 E 2 E 1 E 0
Осциллятор E 3 E 2 E 1 E 0
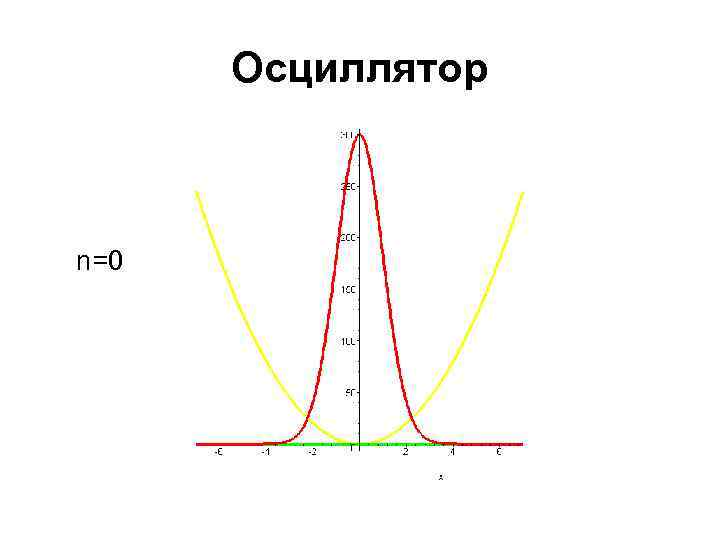 Осциллятор n=0
Осциллятор n=0
 … Осциллятор Волновая функция n=5
… Осциллятор Волновая функция n=5
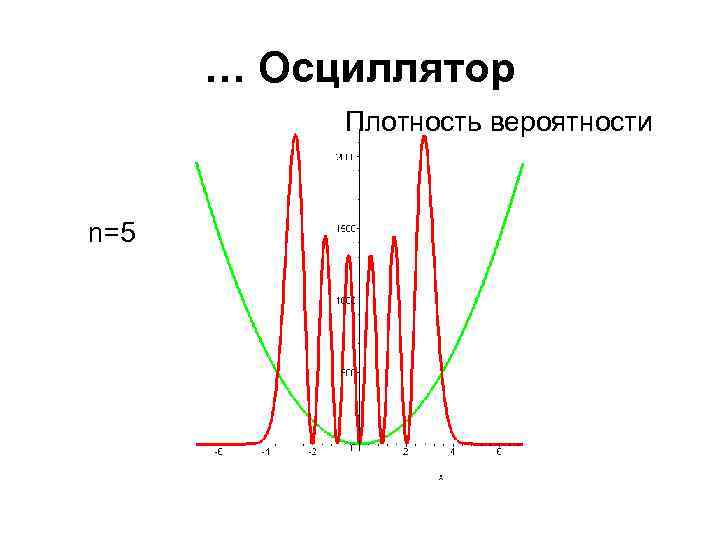 … Осциллятор Плотность вероятности n=5
… Осциллятор Плотность вероятности n=5
 Двумерное уравнение Шредингера y x
Двумерное уравнение Шредингера y x
 Трехмерное уравнение Шредингера
Трехмерное уравнение Шредингера
 Трехмерное уравнение Шредингера. Свободное движение
Трехмерное уравнение Шредингера. Свободное движение
 Волновые свойства • Волна де Бройля • Свободное движение
Волновые свойства • Волна де Бройля • Свободное движение
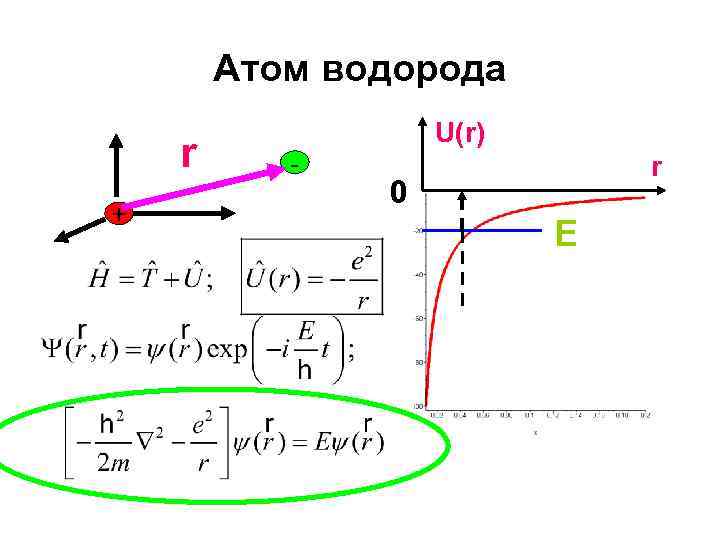 Атом водорода r + - U(r) r 0 E
Атом водорода r + - U(r) r 0 E
 Атом водорода
Атом водорода
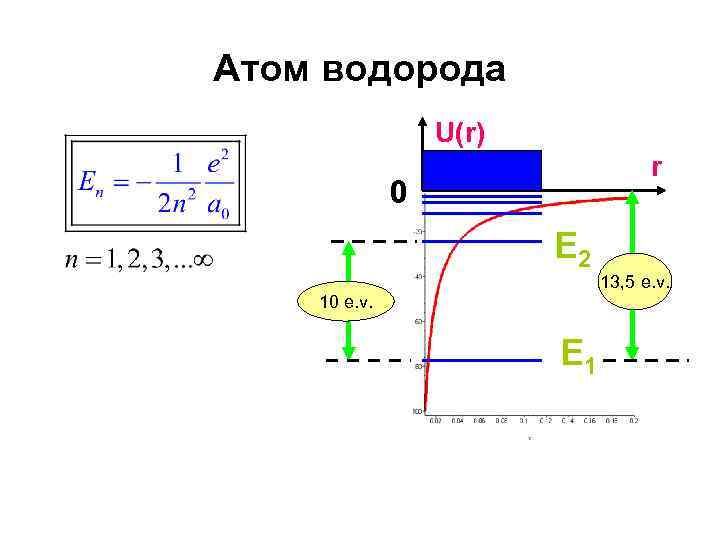 Атом водорода U(r) r 0 E 2 13, 5 e. v. 10 e. v. E 1
Атом водорода U(r) r 0 E 2 13, 5 e. v. 10 e. v. E 1
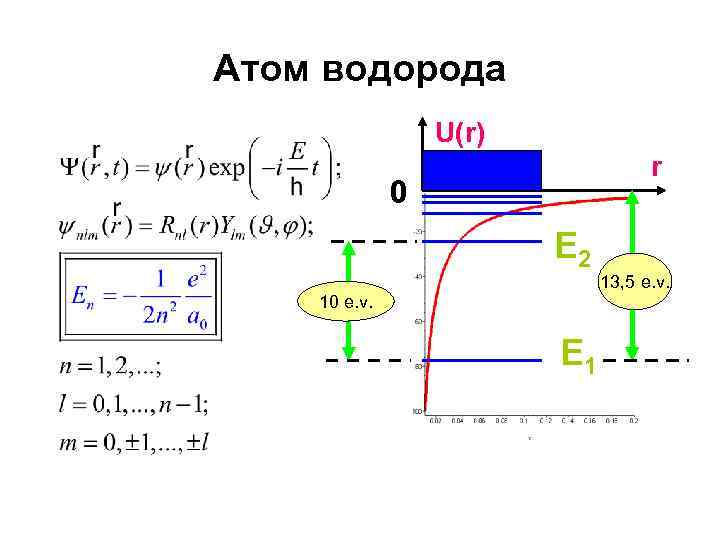 Атом водорода U(r) r 0 E 2 13, 5 e. v. 10 e. v. E 1
Атом водорода U(r) r 0 E 2 13, 5 e. v. 10 e. v. E 1
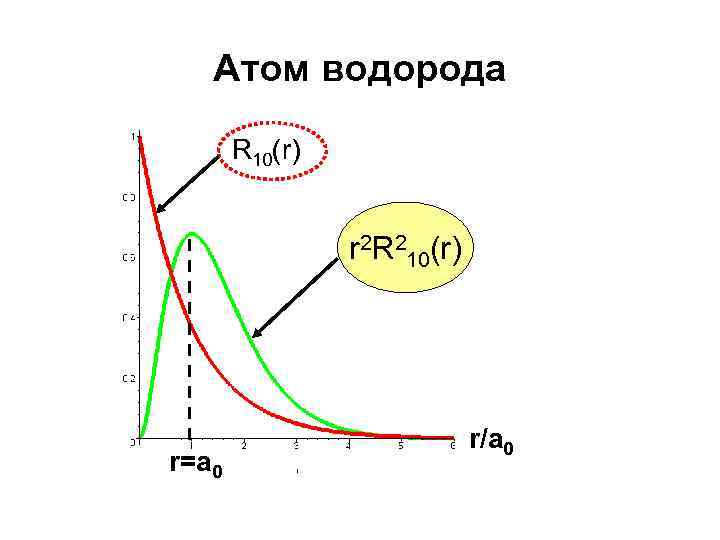 Атом водорода R 10(r) r 2 R 210(r) r=a 0 r/a 0
Атом водорода R 10(r) r 2 R 210(r) r=a 0 r/a 0
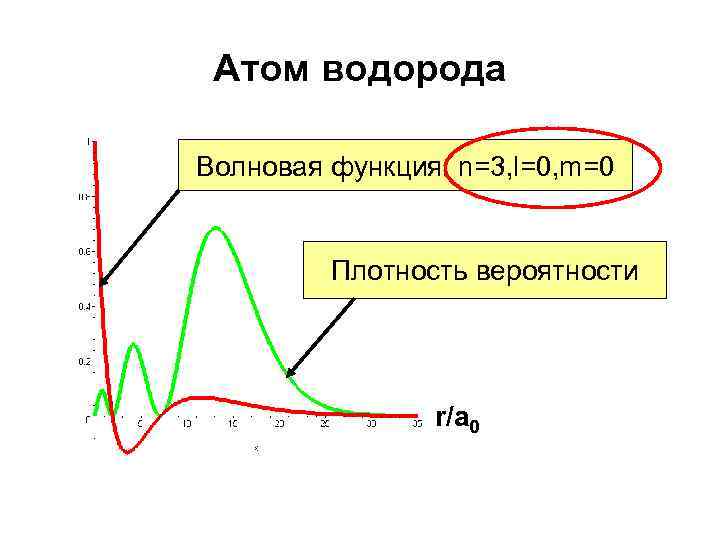 Атом водорода Волновая функция. n=3, l=0, m=0 Плотность вероятности r/a 0
Атом водорода Волновая функция. n=3, l=0, m=0 Плотность вероятности r/a 0
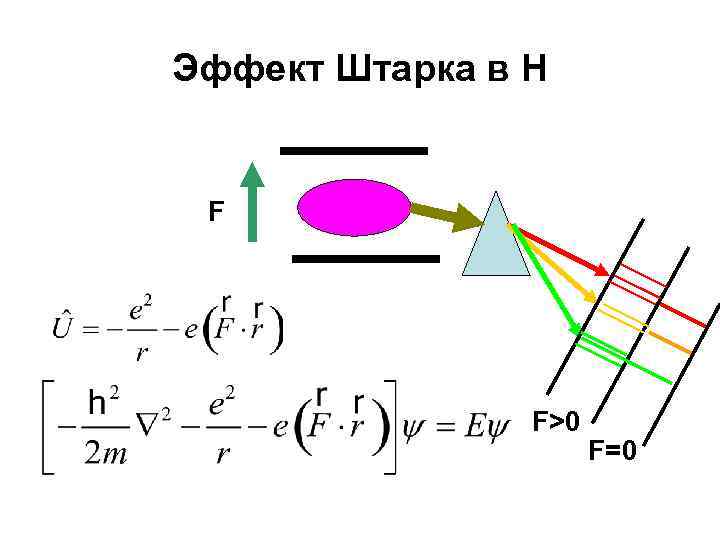 Эффект Штарка в H F F>0 F=0
Эффект Штарка в H F F>0 F=0
 Эффект Зеемана • Расщепление спектральных линий в магнитном поле
Эффект Зеемана • Расщепление спектральных линий в магнитном поле
 Представление операторов
Представление операторов
 Представление операторов
Представление операторов
 Оператор в собственном представлении • Оператор координаты в х представлении– x • Оператор импульса в р представлении - p
Оператор в собственном представлении • Оператор координаты в х представлении– x • Оператор импульса в р представлении - p
 Спин электрона Внешнее поле +h/2 -h/2
Спин электрона Внешнее поле +h/2 -h/2
 Оператор спина
Оператор спина
 Матрицы Паули
Матрицы Паули
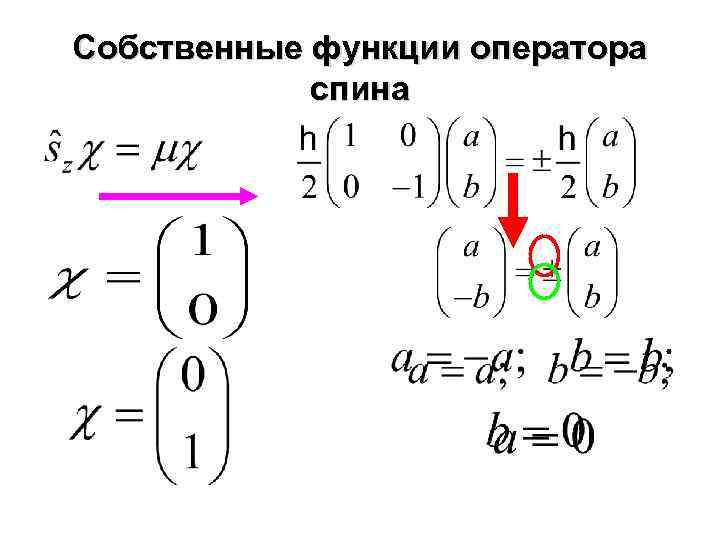 Собственные функции оператора спина
Собственные функции оператора спина
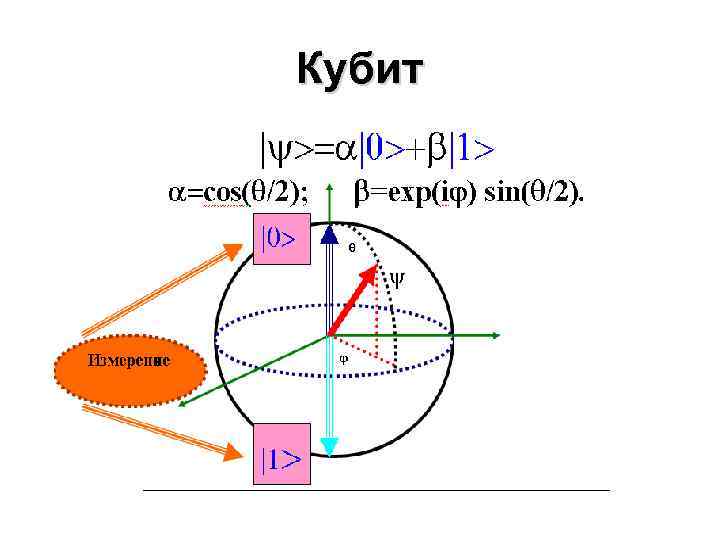 Кубит
Кубит
 Однокубитовые гейты
Однокубитовые гейты
 Многокубитовые гейты
Многокубитовые гейты
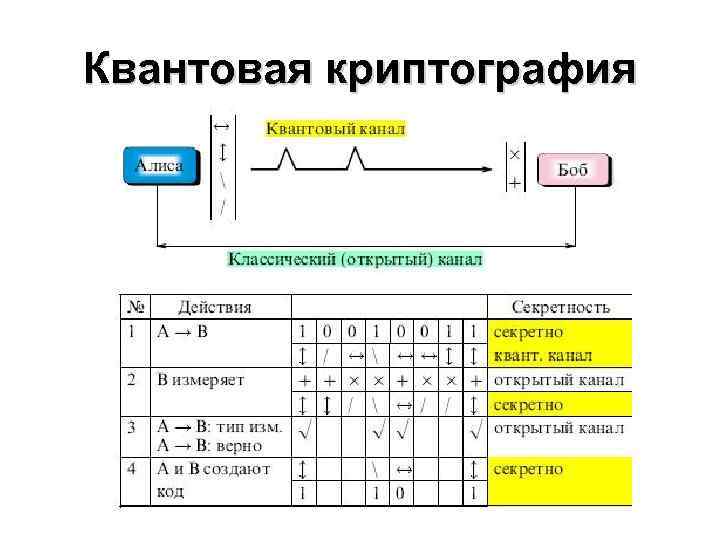 Квантовая криптография
Квантовая криптография
 Уравнение Паули
Уравнение Паули
 Квантовая механика системы частицы • • • Тождественные частицы Оператор перестановки частиц Симметричные состояния Антисимметричные состояния Принцип Паули
Квантовая механика системы частицы • • • Тождественные частицы Оператор перестановки частиц Симметричные состояния Антисимметричные состояния Принцип Паули
 Атом
Атом
 Спектроскопические обозначения n=3 n=2 3 s, 3 p, 3 d 2 s, 2 p l=0, 1, 2, s, p, d -состояния l=0, 1, s, p, - состяния
Спектроскопические обозначения n=3 n=2 3 s, 3 p, 3 d 2 s, 2 p l=0, 1, 2, s, p, d -состояния l=0, 1, s, p, - состяния
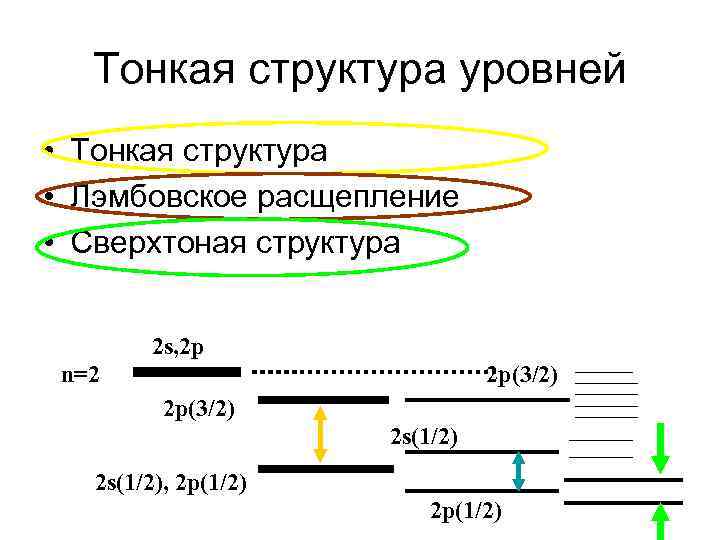 Тонкая структура уровней • Тонкая структура • Лэмбовское расщепление • Сверхтоная структура 2 s, 2 p n=2 2 p(3/2) 2 s(1/2), 2 p(1/2)
Тонкая структура уровней • Тонкая структура • Лэмбовское расщепление • Сверхтоная структура 2 s, 2 p n=2 2 p(3/2) 2 s(1/2), 2 p(1/2)
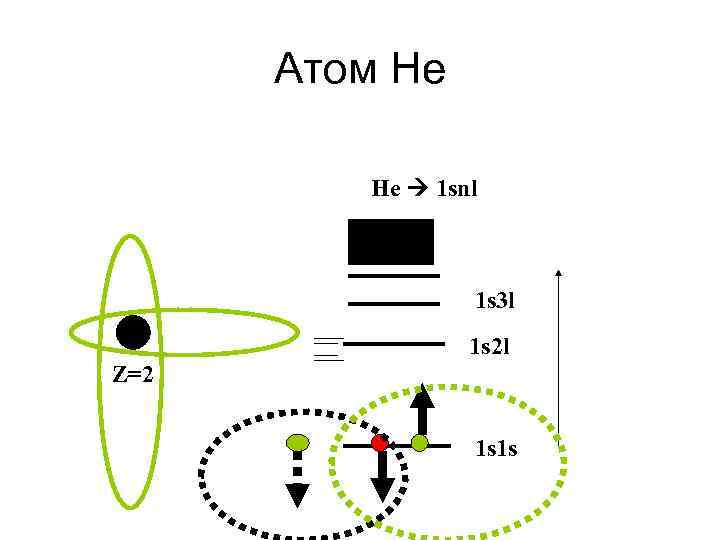 Атом Не He 1 snl 1 s 3 l 1 s 2 l Z=2 1 s 1 s
Атом Не He 1 snl 1 s 3 l 1 s 2 l Z=2 1 s 1 s
 Многоэлектронные атомы • • Литий Li Берилий Be Бор B Углерод С Азот N Кислород O Фтор F Неон Ne (1 s)2 nl Z=3 (1 s) 22 snl Z=4 (1 s) 2(2 s)2 nl Z=5 (1 s) 2(2 s)22 pnl Z=6 (1 s) 2(2 s)2(2 p)2 nl Z=7 (1 s) 2(2 s)2(2 p)3 nl Z=8 (1 s) 2(2 s)2(2 p)4 nl Z=9 (1 s) 2(2 s)2(2 p)5 nl Z=10
Многоэлектронные атомы • • Литий Li Берилий Be Бор B Углерод С Азот N Кислород O Фтор F Неон Ne (1 s)2 nl Z=3 (1 s) 22 snl Z=4 (1 s) 2(2 s)2 nl Z=5 (1 s) 2(2 s)22 pnl Z=6 (1 s) 2(2 s)2(2 p)2 nl Z=7 (1 s) 2(2 s)2(2 p)3 nl Z=8 (1 s) 2(2 s)2(2 p)4 nl Z=9 (1 s) 2(2 s)2(2 p)5 nl Z=10
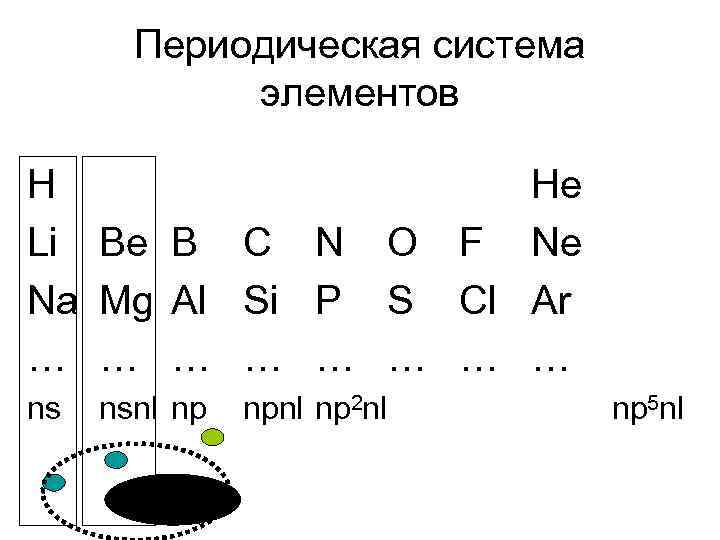 Периодическая система элементов H Li Be B C N O F Na Mg Al Si P S Cl … … … … ns nsnl np npnl np 2 nl He Ne Ar … np 5 nl
Периодическая система элементов H Li Be B C N O F Na Mg Al Si P S Cl … … … … ns nsnl np npnl np 2 nl He Ne Ar … np 5 nl
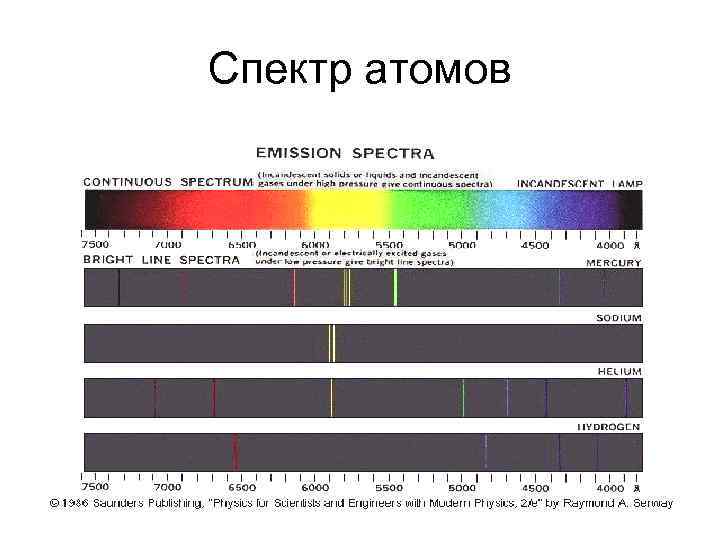 Спектр атомов
Спектр атомов
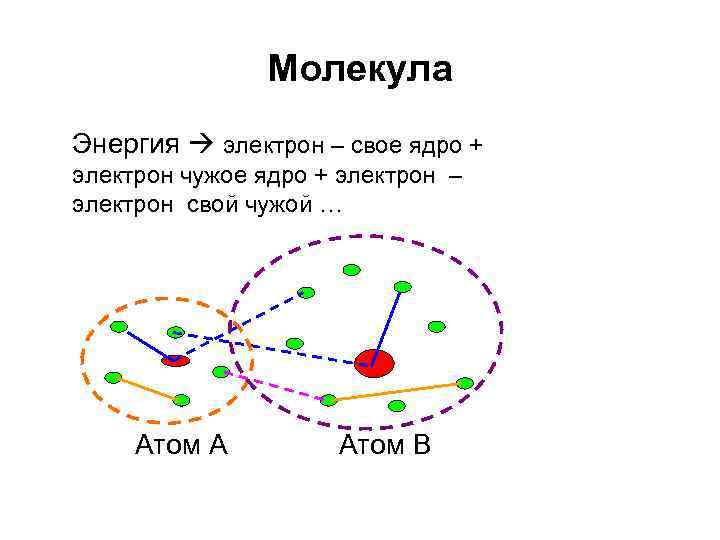 Молекула Энергия электрон – свое ядро + электрон чужое ядро + электрон – электрон свой чужой … Атом А Атом В
Молекула Энергия электрон – свое ядро + электрон чужое ядро + электрон – электрон свой чужой … Атом А Атом В
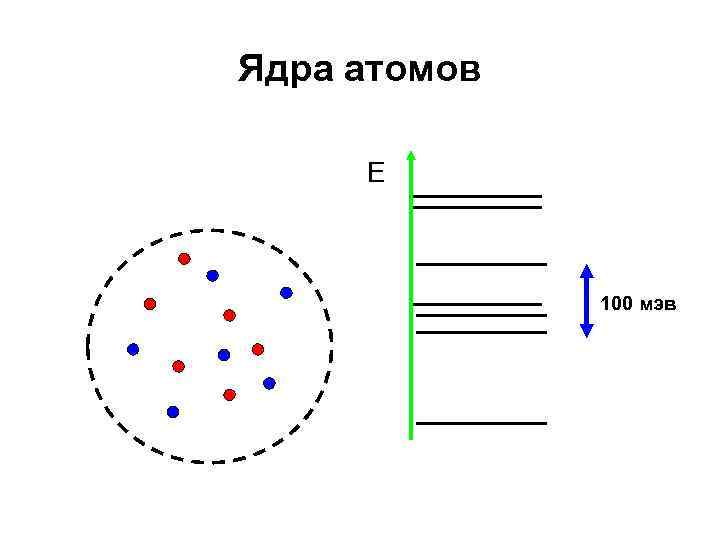 Ядра атомов E 100 мэв
Ядра атомов E 100 мэв
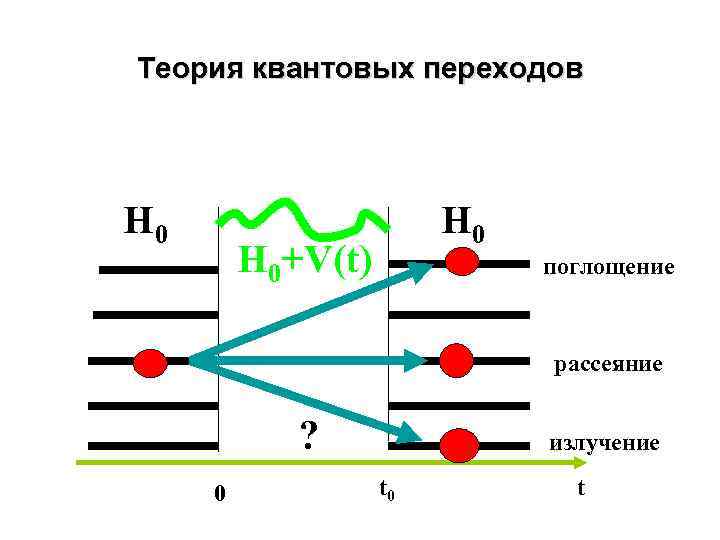 Теория квантовых переходов H 0 H 0+V(t) поглощение рассеяние ? 0 излучение t 0 t
Теория квантовых переходов H 0 H 0+V(t) поглощение рассеяние ? 0 излучение t 0 t
 Теория квантовых переходов
Теория квантовых переходов
 Теория квантовых переходов
Теория квантовых переходов
 Теория квантовых переходов
Теория квантовых переходов
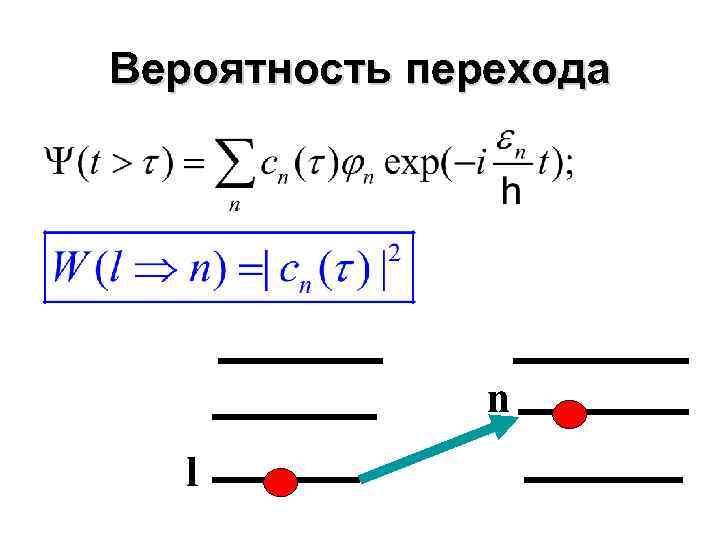 Вероятность перехода n l
Вероятность перехода n l
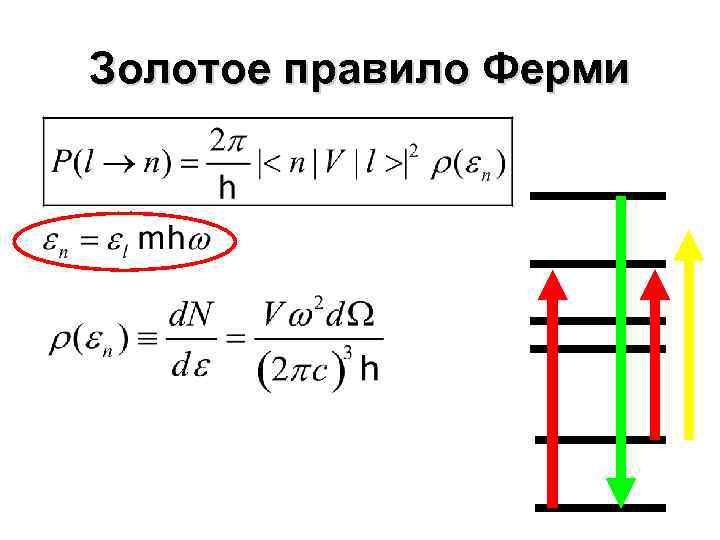 Золотое правило Ферми
Золотое правило Ферми
 § 33. Ток плотности вероятности
§ 33. Ток плотности вероятности
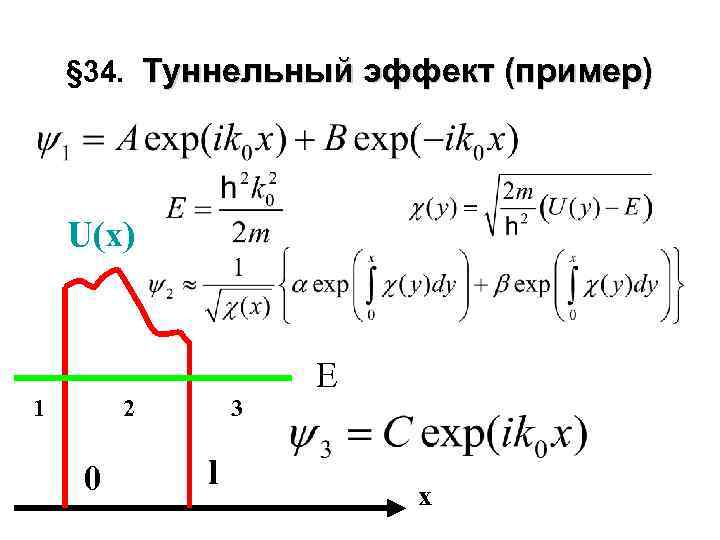 § 34. Туннельный эффект (пример) U(x) 1 2 0 3 l Е x
§ 34. Туннельный эффект (пример) U(x) 1 2 0 3 l Е x
 § 34. … Коэффициенты отражения и прохождения барьера
§ 34. … Коэффициенты отражения и прохождения барьера
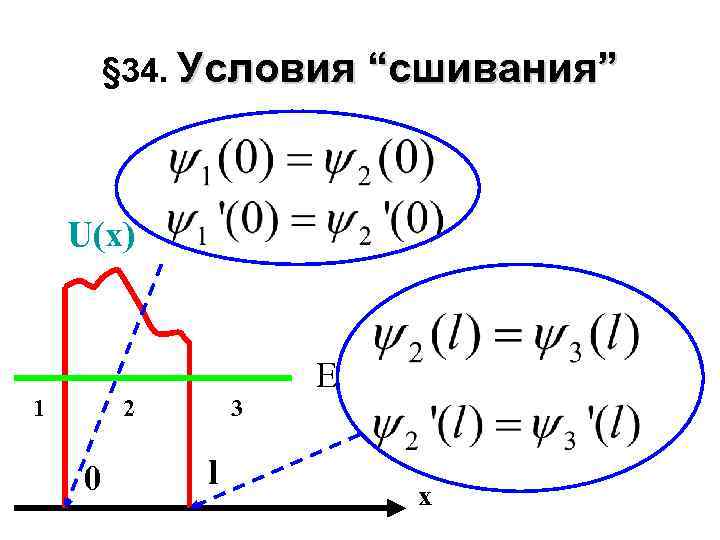 § 34. Условия “сшивания” U(x) 1 2 0 3 l Е x
§ 34. Условия “сшивания” U(x) 1 2 0 3 l Е x
 § 34. … Коэффициент прохождения При увеличении массы от электрона к протону прозрачность уменьшается в 1, 000, 000 раз!
§ 34. … Коэффициент прохождения При увеличении массы от электрона к протону прозрачность уменьшается в 1, 000, 000 раз!
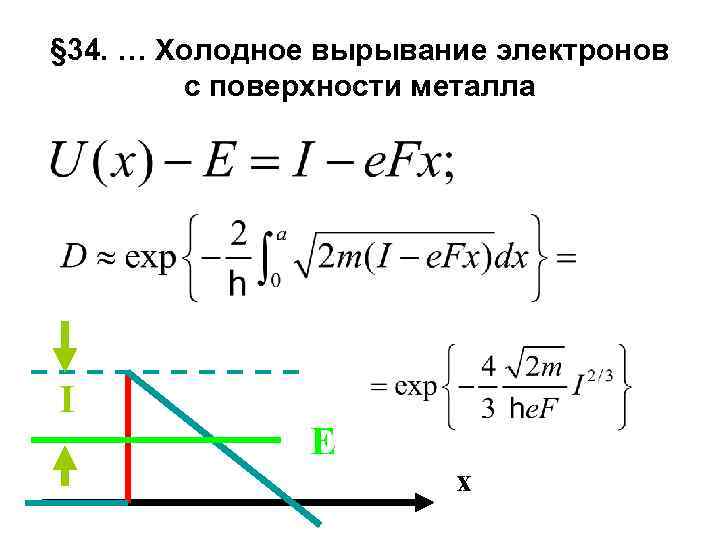 § 34. … Холодное вырывание электронов с поверхности металла I E x
§ 34. … Холодное вырывание электронов с поверхности металла I E x
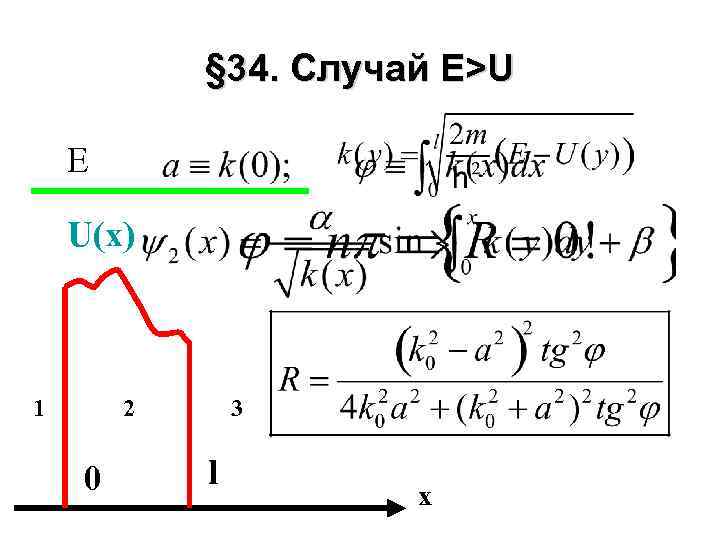 § 34. Случай E>U Е U(x) 1 2 0 3 l x
§ 34. Случай E>U Е U(x) 1 2 0 3 l x
 Квантовые генераторы
Квантовые генераторы
 Квантовые компьютеры
Квантовые компьютеры


