Квантовая механика молекул 63 Колебательно-вращательный спектр двухатомной молекулы

Квантовая механика молекул 63. Колебательно-вращательный спектр двухатомной молекулы. 64. Квантовая механика молекулы водорода. 65. Квантовая теория химических сил.

63. Колебательно-вращательный спектр двухатомной молекулы. 2 атома: A Рис. 1 B r Приведенная масса: Уравнение Шредингера:

Существует 3 вида движения: 1. Поступательное движение – движение как единого целого с центром масс 2. Относительное движение атомов внутри молекулы с Атомы совершают колебательные движения. 3. Молекула может вращаться, то есть вращательное движение атомов относительно центра тяжести

Движение в центральном (сферически симметричном) потенциальном поле Рассмотрим вклады вращательного и внутримолекулярного движений в энергии электронов. Для этого нужно решить уравнение Шредингера: Для гамильтониана:

- приведенная масса. - оператор механического момента орбитального движения атомов молекулы. Гамильтониан описывает энергию вращательного и внутримолекулярного движения. Поступательное движение не учитываем. Это уравнение записывается для центрального потенциального поля:

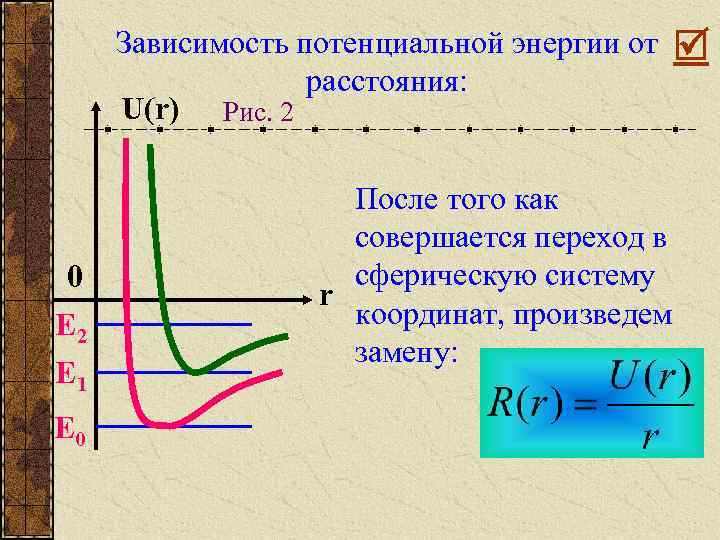
Зависимость потенциальной энергии от расстояния: U(r) Рис. 2 0 E 2 E 1 E 0 После того как совершается переход в сферическую систему r координат, произведем замену:

Появляется добавка, это кинетическая энергия орбитального движения атомов в молекуле. Получается, если молекула сильно раскрутится, то она распадается, происходит диссоциация молекулы. Вместо обычной потенциальной энергии, появляется эффективная потенциальная энергия взаимодействия. Можно ввести:

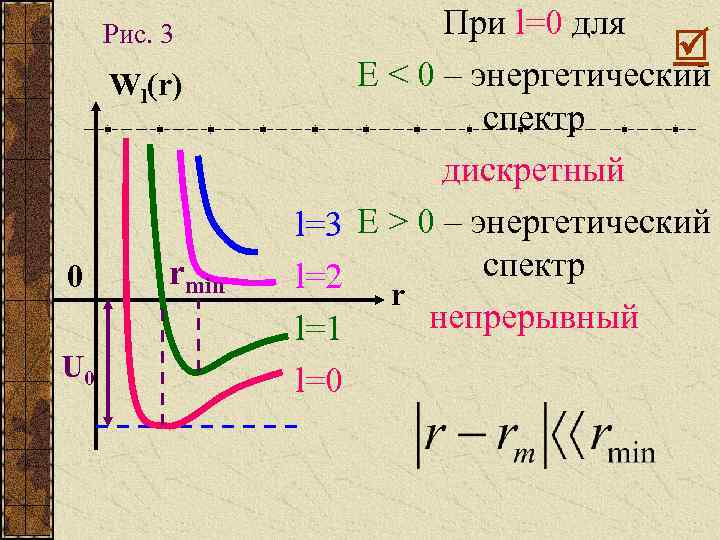
Рис. 3 Wl(r) 0 U 0 rmin При l=0 для Е < 0 – энергетический спектр дискретный l=3 Е > 0 – энергетический спектр l=2 r непрерывный l=1 l=0

Положение точки равновесия, где силы притяжения и отталкивания равны между собой: rmin=rl =0

Разложение начинается с квадратичного вклада: Запишем уравнение Шредингера для ЛГО: - частота связанная с вращательным квантовым числом

Запишем энергию вращательного движения молекулы в целом: Относительно минимума частицы совершаются малые колебания. В итоге: x 0 – амплитуда ЛГО

- Энергия осциллятора Полная энергия складывается из трех энергий: гармонических колебаний, энергии равновесия и энергии вращательного движения

Для молекулы водорода Колебательный квант: Вращательный квант: Здесь Энергия диссоциации Из-за того, что есть нулевые колебания, существует нулевая энергия: Так как n =0

- энергия электрона в атоме - атомная энергия - кинетическая энергия вращения всей молекулы - энергия внутримолекулярных колебаний

Рис. 4 n=2 n=1 n=0 l=2 В итоге: кроме одной l=1 линии возникают l=0 полосы. Линейный или полосатый спектр двух атомной молекулы. Это l=2 энергетический спектр. l=1 Но это не спектр l=0 переходов между уровнями. Такой спектр l=3 l=2 будет другим. Он l=1 складывается из l=0 переходов:

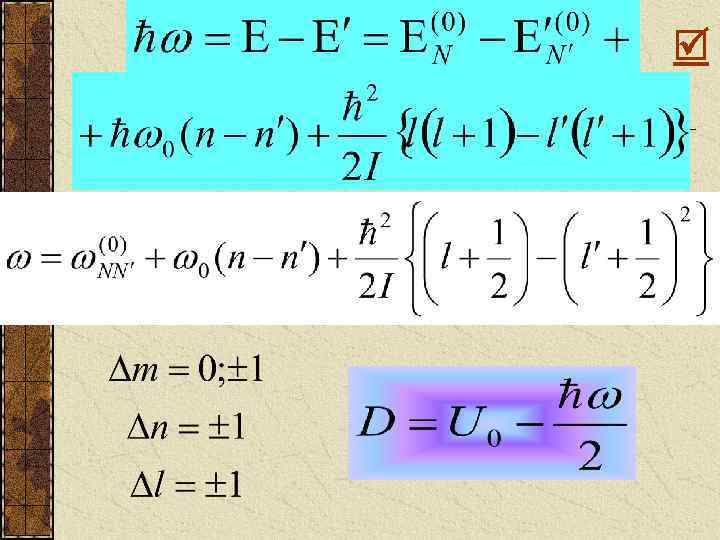
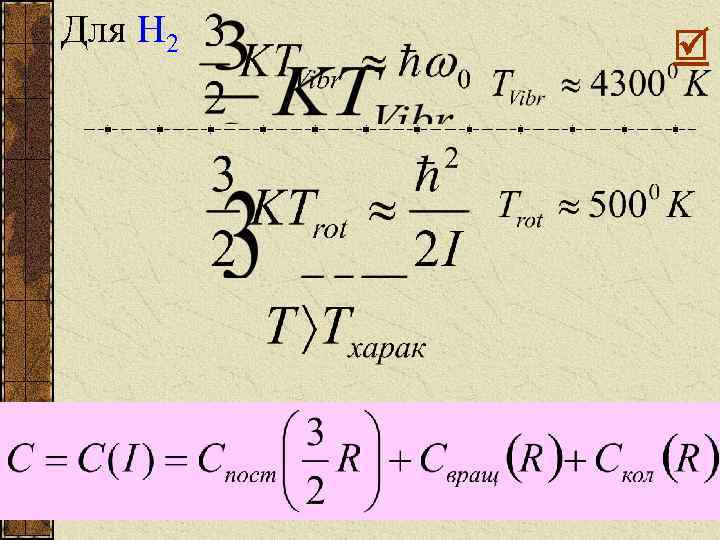
Для H 2

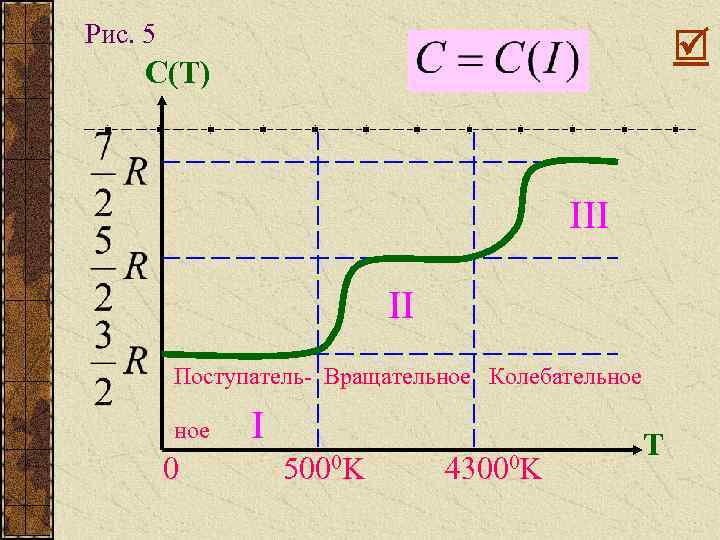
Рис. 5 С(Т) III II Поступатель- Вращательное Колебательное 0 I 5000 K 43000 K Т

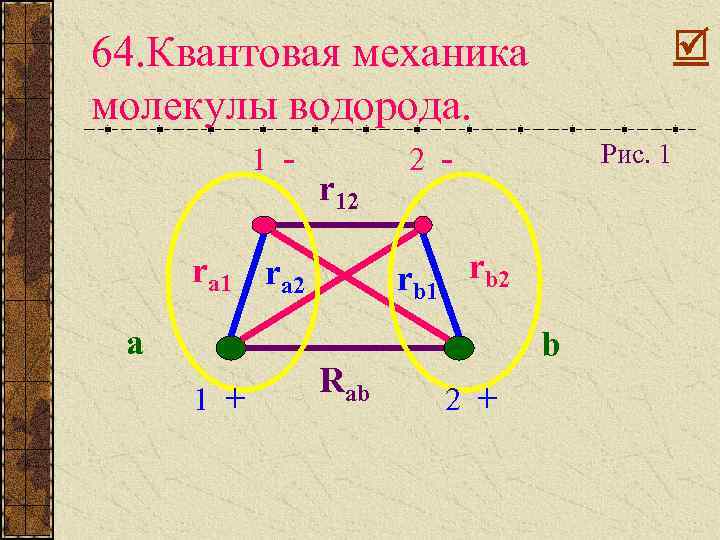
64. Квантовая механика молекулы водорода. 1 - r 12 rb 1 rb 2 ra 1 ra 2 a 1 + Рис. 1 2 - Rab b 2 +

Задача: надо объяснить при каких условиях возникает между атомами притяжение. Энергия взаимодействия двух атомов: Запишем уравнение Шредингера: Представим гамильтониан в виде трех вкладов:

При приближении атомов друг к другу произойдет образование электронного облака. Оно свяжет два атома в единую устойчивую молекулу. Если атомы развести, то будет два отдельных атома водорода. Поэтому полная энергия зависит от расстояния между двумя ядрами и добавки, которая обеспечивает взаимное притяжение. Если поменять два электрона местами, ничего не изменится, но возникает обменное выражение. Облака разные, а энергия одна и та же. Эта задача легко решается при помощи теории возмущения:

E 0 – основное состояние атома H

2 состояния: 1. Ортоводород 2. Пара - водород

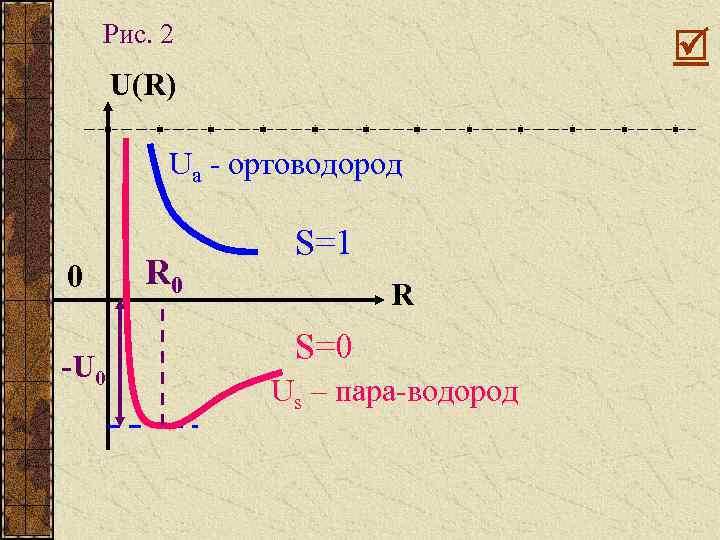
Рис. 2 U(R) Ua - ортоводород 0 -U 0 R 0 S=1 R S=0 Us – пара-водород

Общая энергия: потенциальная энергия симметричная и антисимметричная - обычная энергия удвоенных атомов - энергия отталкивания

К – средняя энергия электростатического взаимодействия А – обменная энергия S 2 – квантово механический интеграл перекрытия волновых функций

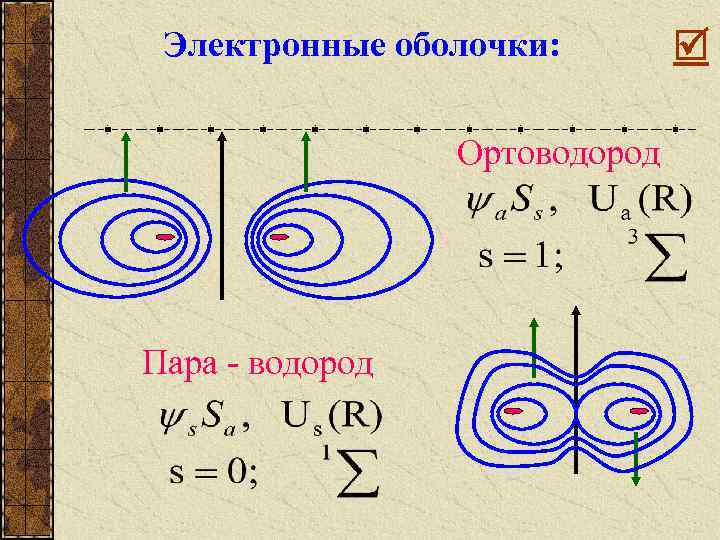
Электронные оболочки: Ортоводород Пара - водород

65. Квантовая теория химических сил. Химические связи: ионные и ковалентные. Ионная связь реализуется в тех случаях, когда молекулу можно представить как образование из положительных и отрицательных ионов. Ковалентная связь реализуется в тех случаях, когда деление на ионы провести невозможно. Ионные силы возникают между ионами, когда электронное облако замкнуто в пространстве около иона. Ковалентные связи обусловлены наличием общего электронного облака.

Классическая физика позволяет понять существование ионов. Ковалентную связь можно объяснить только на основе квантовой механики, так ковалентная связь создается за счет обменных взаимодействий. А+ принцип тождественности частиц H 2, H 3, H 4. Существует только Н 2, так как в случае Н 3 Н 4 устойчивых молекул нет, из-за того, что спин не равен нулю

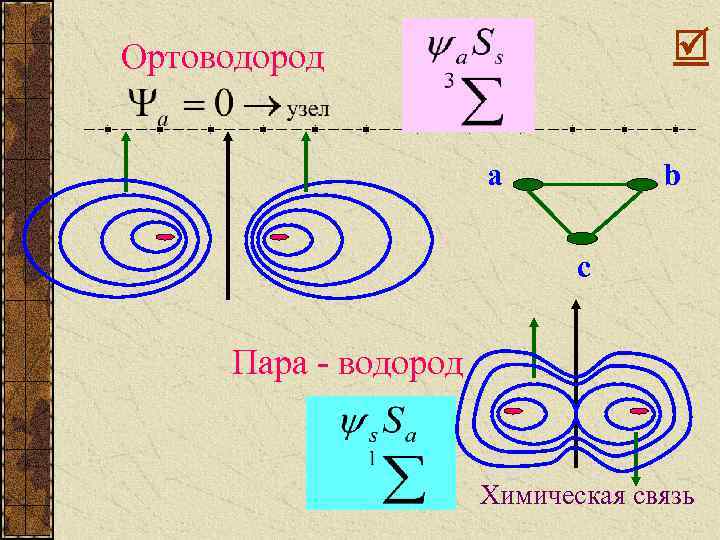
Ортоводород a b c Пара - водород Химическая связь

Можно показать, что химические силы обладают свойством насыщения. Если молекуле Н 2 добавить третий атом Н, то возникнет новая волновая функция. Она должна быть ассиметроичной, но минимальный суммарный спин +1/2. Поэтому не будет общего волнового облака, будет возникать отталкивание. Пусть Полная волновая функция должна быть антисимметричной:

Единственная асимметричная функция:

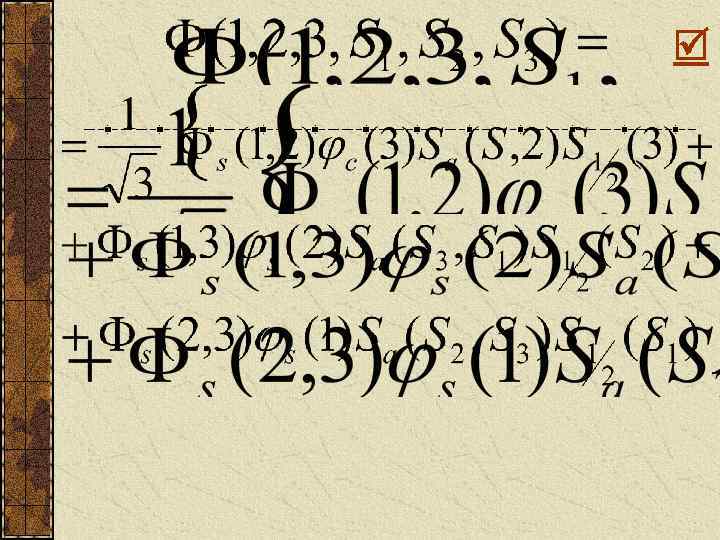
Вероятность положения электронов в окрестности точек

Вопросы ? Опишите три вида движения. ? Из каких вкладов состоит гамильтониан атома водорода? ? Виды химических связей. Описать их. ? Опишите орто- и пара водород.