Скачать презентацию Квантовая механика многоэлектронных атомов 60 Квантовая механика многоэлектронных Скачать презентацию Квантовая механика многоэлектронных атомов 60 Квантовая механика многоэлектронных

12.Квантовая механика многоэлектронных атомов..ppt

  • Количество слайдов: 41

Квантовая механика многоэлектронных атомов 60. Квантовая механика многоэлектронных атомов. Качественная теория атома гелия. 61. Квантовая механика многоэлектронных атомов 60. Квантовая механика многоэлектронных атомов. Качественная теория атома гелия. 61. Приближенная количественная теория атома гелия. 62. Квантовая механика и периодическая система элементов Д. И. Менделеева.

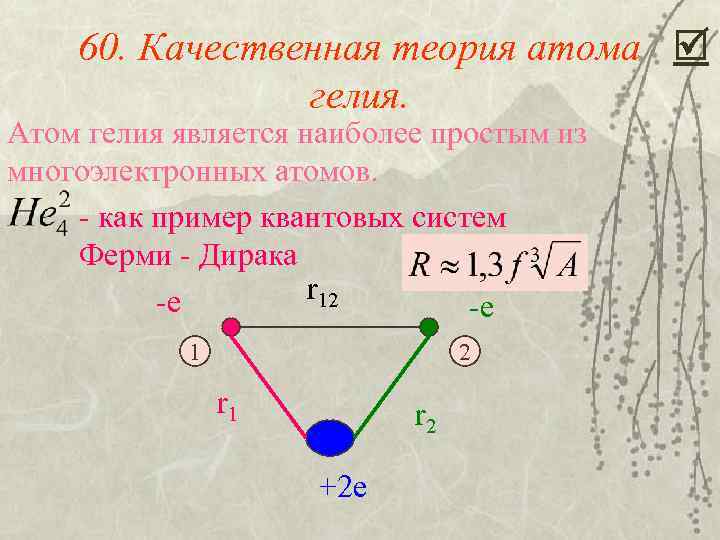60. Качественная теория атома гелия. Атом гелия является наиболее простым из многоэлектронных атомов. - 60. Качественная теория атома гелия. Атом гелия является наиболее простым из многоэлектронных атомов. - как пример квантовых систем Ферми - Дирака r 12 -е -е 1 2 r 1 r 2 +2 е

Решаем уравнение Шредингера для данной системы: Определим вид оператора гамильтониана для электронов атома гелия: Решаем уравнение Шредингера для данной системы: Определим вид оператора гамильтониана для электронов атома гелия: Взаимодействия состоят из двух групп. 1. Кулоновские взаимодействия между ядром и электронами:

- оператор кинетической энергии первого электрона - оператор кинетической энергии второго электрона - кулоновская - оператор кинетической энергии первого электрона - оператор кинетической энергии второго электрона - кулоновская энергия взаимодействия 2. Слабое магнитное взаимодействие, обусловленное взаимодействием спинов электронов между собой.

Запишем полную волновую функцию двух электронов атома гелия в виде: 1 -координатная волновая Запишем полную волновую функцию двух электронов атома гелия в виде: 1 -координатная волновая функция - спиновая волновая функция

Разделим на координатные и волновые функции. Электроны – фермионы должны быть антисимметричны, поэтому: 2 Разделим на координатные и волновые функции. Электроны – фермионы должны быть антисимметричны, поэтому: 2 Поскольку волновая функция разделена, то оператор перестановки можно представить в виде произведения двух операторов перестановки: 3 -действует на координатную часть - действует на спиновую часть

3 и 1 подставляем в 2 Есть 2 случая. Этот минус «-» сначала подставляем 3 и 1 подставляем в 2 Есть 2 случая. Этот минус «-» сначала подставляем в координатную часть к Ф, а потом в спиновую часть к S:

I У спиновой функции знак плюс «+» Координатная часть антисимметрична а спиновая – симметрична I У спиновой функции знак плюс «+» Координатная часть антисимметрична а спиновая – симметрична Тогда полная волновая функция:

II У спиновой функции знак минус «-» Координатная часть симметрична а спиновая – симметрична II У спиновой функции знак минус «-» Координатная часть симметрична а спиновая – симметрична Тогда полная волновая функция:

Найдем спиновые волновые функции. Каждую функцию можно написать в виде произведения спиновых функций, относящихся Найдем спиновые волновые функции. Каждую функцию можно написать в виде произведения спиновых функций, относящихся к каждому электрону в отдельности: - указывают направление спина электрона относительно оси ОZ

А Рассмотрим антисимметричную полную спиновую функцию (спины направлены противоположно) Суммарный спин для антисимметричного спинового А Рассмотрим антисимметричную полную спиновую функцию (спины направлены противоположно) Суммарный спин для антисимметричного спинового состояния: + -

То есть Это состояние называется синглетным, когда спиновые функции антисимметричные, а координатные функции симметричные. То есть Это состояние называется синглетным, когда спиновые функции антисимметричные, а координатные функции симметричные. В таком состоянии гелий называется - Пара-гелий синглет

Б Если спины электронов параллельны, то антисимметричные состояния невозможны Расщепляем на произвольные односпиновые функции Б Если спины электронов параллельны, то антисимметричные состояния невозможны Расщепляем на произвольные односпиновые функции

В этом случае мы можем иметь следующие состояния спина электронов: 1. 2. 3. В этом случае мы можем иметь следующие состояния спина электронов: 1. 2. 3.

3 состояния: + + - - 2 S+1=3 – триплетное состояние В таком состоянии 3 состояния: + + - - 2 S+1=3 – триплетное состояние В таком состоянии когда спиновая функция симметричная, а координатная функция антисимметричная гелий называется - Орто-гелий

Вспомним о свойствах ЛГО: То есть, возбужденное состояние соответствует узлу (n = число узлов). Вспомним о свойствах ЛГО: То есть, возбужденное состояние соответствует узлу (n = число узлов). Чем больше узлов, тем больше энергия. У пара -гелия симметричная, у орто-гелия антисимметричная координатная функция. То есть хотя бы на один узел там больше, значит это состояние принадлежит к большей энергии.

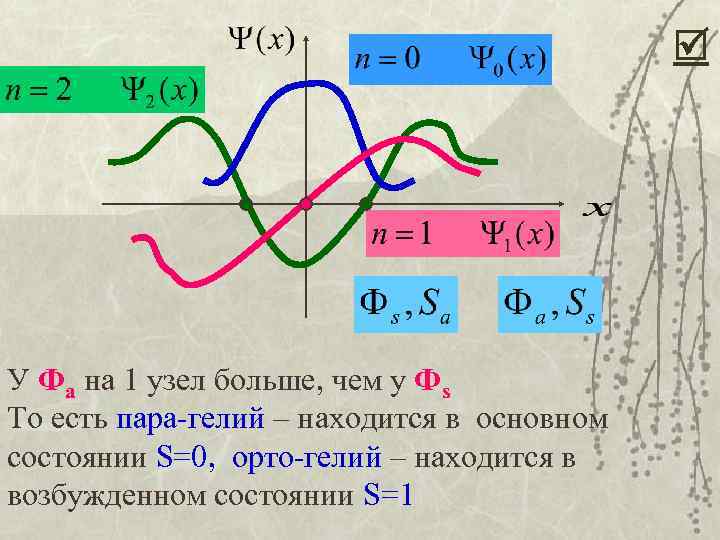У Фа на 1 узел больше, чем у Фs То есть пара-гелий – У Фа на 1 узел больше, чем у Фs То есть пара-гелий – находится в основном состоянии S=0, орто-гелий – находится в возбужденном состоянии S=1

61. Приближенная количественная теория атома гелия. Расчитаем квантовые уровни атома гелия. Рассмотрим уравнение Шредингера: 61. Приближенная количественная теория атома гелия. Расчитаем квантовые уровни атома гелия. Рассмотрим уравнение Шредингера: Если принибречь спиново-орбитальными взаимодействиями, тогда гамильтониан имеет вид:

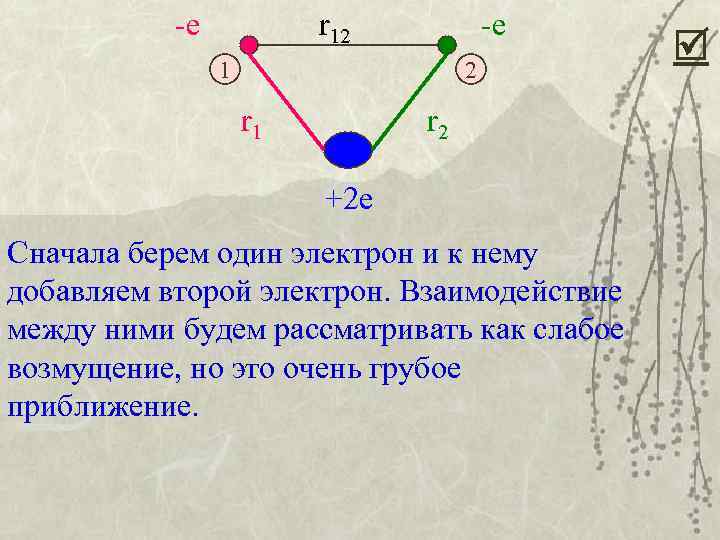-е r 12 -е 1 2 r 1 r 2 +2 е Сначала берем -е r 12 -е 1 2 r 1 r 2 +2 е Сначала берем один электрон и к нему добавляем второй электрон. Взаимодействие между ними будем рассматривать как слабое возмущение, но это очень грубое приближение.

Оператор - оператор полной энергии двух электронов в поле ядра без взаимодействия их между Оператор - оператор полной энергии двух электронов в поле ядра без взаимодействия их между собой. - энергия взаимодействия электронов (как малая поправка)

Представим, что 1 -й электрон находится в n-ом квантовом состоянии: 2 -й электрон возьмем Представим, что 1 -й электрон находится в n-ом квантовом состоянии: 2 -й электрон возьмем в другом состоянии, состояние - m Если это так, то полная волновая функция нулевого приближения будет выглядеть следующим образом: 1

Но электроны можно поменять местами: Получилось другое состояние, то есть волновые функции, облака изменились, Но электроны можно поменять местами: Получилось другое состояние, то есть волновые функции, облака изменились, а энергия осталась та же самая - двукратное вырождение Когда энергия одна, а волновые функции разные, такое состояние называется вырожденным состоянием. Это случай обменного вырождения. Мы имеем дело с теорией возмущений для двукратно вырожденного случая. 2

Применим теорию возмущений для двукратно вырожденного случая: вопрос N 45. 3 - кулоновское отталкивание Применим теорию возмущений для двукратно вырожденного случая: вопрос N 45. 3 - кулоновское отталкивание 4

5 К и А – энергии кулоновского взаимодействия, они обе разные. К – это 5 К и А – энергии кулоновского взаимодействия, они обе разные. К – это средняя энергия кулоновского взаимодействия двух электронов. К- любой из диагональных объектов. и - разные функции. Второе состояние получается из первого обменом квантовыми состояниями электронов.

Поэтому А называют обменной энергией. Понятие обменной энергии существует только в квантовой механике и Поэтому А называют обменной энергией. Понятие обменной энергии существует только в квантовой механике и связано с неразличимостью 6 У орто-гелия К-А, у пара-гелия К+А. Поправки к энергии отличаются знаком обменной энергии. В разных спиновых состояниях влияние обменной энергии разное, оно зависит от спина электронной оболочки.

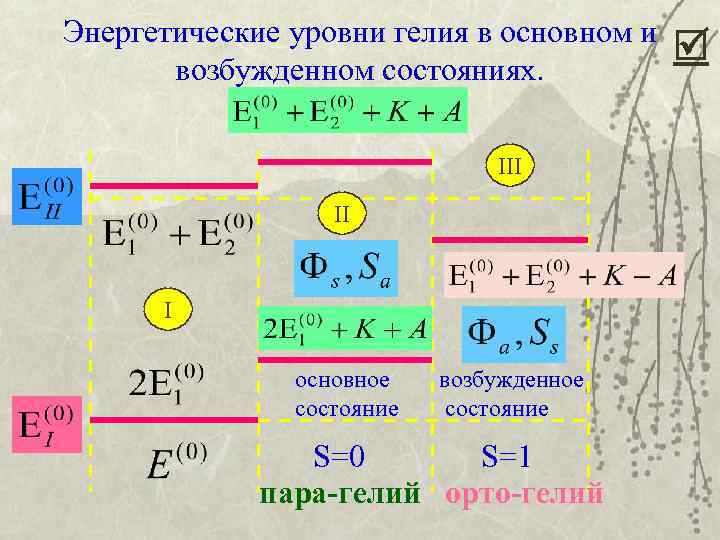Энергетические уровни гелия в основном и возбужденном состояниях. III II I основное состояние возбужденное Энергетические уровни гелия в основном и возбужденном состояниях. III II I основное состояние возбужденное состояние S=0 S=1 пара-гелий орто-гелий

62. Квантовая механика и периодическая система элементов Д. И. Менделеева. Периодичность свойств химических элементов 62. Квантовая механика и периодическая система элементов Д. И. Менделеева. Периодичность свойств химических элементов тесно связана с периодичностью занятия внешних электронных оболочек атомов этой таблицы. Начнем строить электронные оболочки: Главное в описании: Z –изотопы, порядковый номер или заряд.

А – атомный вес. Устойчивый атом – это атом с наименьшей энергией: - главное А – атомный вес. Устойчивый атом – это атом с наименьшей энергией: - главное квантовое число - орбитальное квантовое число - квантовое число полного механического момента - магнитное квантовое число

Электроны подчиняются запрету Паули: не может быть одинаковый набор квантовых чисел в одном и Электроны подчиняются запрету Паули: не может быть одинаковый набор квантовых чисел в одном и том же состоянии. Z=1 H 1 электрон - электронная конфигурация - основное состояние электронной оболочки атома водорода.

Z=2 Hе 2 электрона: 1 как у H, второй: - электронная конфигурация Суммарный орбитальный Z=2 Hе 2 электрона: 1 как у H, второй: - электронная конфигурация Суммарный орбитальный момент: Суммарный спиновый момент: - квантовое число полного механического момента - основное состояние атома гелия

Z=3 Li 3 электрона: 2 как у He, третий: - электронная конфигурация Суммарный орбитальный Z=3 Li 3 электрона: 2 как у He, третий: - электронная конфигурация Суммарный орбитальный момент: Суммарный магнитный момент: Суммарный спиновый момент:

квантовое число полного механического момента: - основное состояние электронной оболочки атома гелия. квантовое число полного механического момента: - основное состояние электронной оболочки атома гелия.

Z=4 Be 4 электрона: 3 как у Li, 4 -ый: - электронная конфигурация Суммарный Z=4 Be 4 электрона: 3 как у Li, 4 -ый: - электронная конфигурация Суммарный орбитальный момент: Суммарный магнитный момент: Суммарный спиновый момент: - квантовое число полного механического момента - основное состояние электронной оболочки атома бериллия.

Z=5 B 5 электронов: 4 как у Be, 5 -ый: - электронная конфигурация Суммарный Z=5 B 5 электронов: 4 как у Be, 5 -ый: - электронная конфигурация Суммарный орбитальный момент: Суммарный магнитный момент: Суммарный спиновый момент: - квантовое число полного механического момента - основное состояние электронной оболочки атома бора.

Z=6 C 6 электронов: 5 как у B, 6 -oй: - электронная конфигурация Суммарный Z=6 C 6 электронов: 5 как у B, 6 -oй: - электронная конфигурация Суммарный орбитальный момент: Суммарный спиновый момент: - квантовое число полного механического момента - основное состояние электронной оболочки атома углерода.

Z=7 N 7 электронов: 6 как у C, 7 -oй: - электронная конфигурация - Z=7 N 7 электронов: 6 как у C, 7 -oй: - электронная конфигурация - основное состояние электронной оболочки.

Z=8 O 8 электронов: 7 как у N, 8 -oй: Z=9 F 9 электронов: Z=8 O 8 электронов: 7 как у N, 8 -oй: Z=9 F 9 электронов: 8 как у O, 9 -ый:

Z=10 Ne 10 электронов: 9 как у F, 10 -ый: - электронная конфигурация Суммарный Z=10 Ne 10 электронов: 9 как у F, 10 -ый: - электронная конфигурация Суммарный орбитальный момент: Суммарный спиновый момент: - квантовое число полного механического момента - основное состояние

В таблице есть: Щелочные Li, Na, K, Rb, Cs, Fr металлы: Z = 3, В таблице есть: Щелочные Li, Na, K, Rb, Cs, Fr металлы: Z = 3, 11, 19, 37, 55, 87 После инертных газов в таблице находятся щелочные металлы. У них во внешней электронной оболочке один электрон, он может легко уйти. Они химически агрессивные элементы. Металлы характеризуются электропроводимостью.

F, Cl, Br, J, Z = 9, 17, 35, 53, У них во F, Cl, Br, J, Z = 9, 17, 35, 53, У них во внешней электронной оболочке не хватает одного электрона, поэтому они берут один электрон. Они химически агрессивны. Инертные He, Ne, Ar, Kr, Xe, Rn газы: Z = 2, 10, 18, 36, 54, 86 Галоиды: У них внешняя электронная оболочка сферически симметрична, то есть полностью заполнена, плотно упакована. Они плохо вступают в реакции, так как не могут отдать или взять электрон.

Вопросы ? В каком состоянии гелий называется ортогелием? ? Чем отличаются щелочные металлы от Вопросы ? В каком состоянии гелий называется ортогелием? ? Чем отличаются щелочные металлы от галогенов и инертных газов?