Квантовая логика Введение Квантовая механика раздел

Квантовая логика

Введение Квантовая механика — раздел теоретической физики, описывающий квантовые системы и законы их движения. Классическая механика, хорошо описывающая системы макроскопических масштабов, не способна описать явления на уровне атомов, электронов и фотонов. Квантовая механика способна с великолепной точностью описывать электроны, фотоны, а также другие элементарные частицы. Эксперименты подтверждают результаты, полученные с помощью квантовой механики.

Введение Возникновение квантовой механики, пришедшей на смену классической механике Ньютона, произвело подлинный переворот в физическом мышлении. В частности, вывод о недетерминированности Вселенной долго не давал покоя ученым начала XX века Пересмотр традиционных представлений привел к возникновению идеи особой логики квантовой механики(квантовой логики).

Введение Предполагалось, что теории классической физики, описывающие факты, опираются на законы обычной логики — логики макромира; квантовая же физика имеет дело не просто с фактами, а с их вероятностными связями, и в ней рассуждают, опираясь на совершенно иные схемы мышления. Выявление и систематическое описание последних — задача специальной логики микромира.

Цель работы В своей работе я попытаюсь понять, чем же отличается логика микромира от типичной логики макромира. Действительно ли квантовая механика руководствуется особой логикой? Что она из себя представляет? Влияние квантовой механики на современные фундаментальные и прикладные науки трудно переоценить, поэтому очень важно понять логику этой, без сомнения, грандиозной теории.

Определение Квантовая логика - раздел логики, необходимый для рассуждения о предложениях, которые учитывают принципы квантовой теории. В этой работе я буду считать термины «Логика Квантовой Механики» и «Квантовая логика» взаимозаменяемыми, хотя некоторые исследователи иногда различают эти понятия.

Особенности квантовой логики У квантовой логики существует множество вариаций. Эти «квантовые логики» серьезно различаются как множествами принимаемых в них законов, так и способами своего обоснования. Чаще всего в них отказываются от классических законов дистрибутивности и ассоциативности, касающихся сложных утверждений, построенных с помощью союзов «и» и «или» . Иногда отбрасывается даже закон исключенного третьего.

Особенности квантовой логики Основной особенностью является отсутствие классического закона дистрибутивности, которое я рассмотрю на двух примерах: Дифракция электрона Измерение дополнительных величин

Дифракция электрона Рассмотрим мысленный эксперимент с прохождением электрона через одну и две щели экрана. Пусть высказывание А означает «электрон проходит через первую щель» , высказывание B означает «электрон проходит через вторую щель» , высказывание C означает «электрон оставляет на фотопластинке-мишени точечный след» . В этом случае высказывание (A/B)/C истинно в случае, когда открыта одна из щелей. Если открыты обе щели, то ситуация, казалось бы, должна описываться высказыванием (A/C)/(B/C), т. е. электрон проходит через первую щель и оставляет точечный след, либо электрон проходит через вторую щель и оставляет точечный след на фотопластинке-мишени.

Дифракция электрона Согласно закону дистрибутивности (A/B)/C= (A/C)/(B/C) и тождество истинно в силу того, что обе части описывают один и тот же результат — точечный след на мишени. На самом же деле на фотопластинке мы получаем дифракционную картину и нарушение закона дистрибутивности.

Измерение дополнительных величин Рассмотрим движущуюся по прямой частицу. Далее, пусть логические переменные p, q и r имеют следующие значения: p = «частица двигается вправо» ; q = «частица слева от начала координат» ; Принцип неопределённости r = «частица справа от начала координат» . Тогда предложение «q или r» всегда верно, точно как и «p и (q или r)» С другой стороны, «p и q» и «p и r» неверны, так как требуют более жёстких условий одновременных значений координаты и импульса, что не возможно по принципу неопределённости Гейзенберга. Поэтому «(p и q) или (p и r)» неверно и дистрибутивность не может существовать. Рассмотрим отношение дополнительности более подробно.

Логическая система, формализующая квантовый эффект дополнительности Две величины называются дополнительными, если они одновременно ненаблюдаемы(см. принцип неопределенности выше). К таким относятся, например, координата и импульс, энергия и время и т. д. Пусть Т есть множество предложений квантово-механической теории, в которой содержится принцип дополнительности. Поставим задачу описать логическую систему для этой теории, придерживаясь семантического направления. В качестве возможных истинностных значений для предложений из {Т} введем следующее: логически истинно (ЛИ), логически ложно (ЛЛ), фактически истинно (ФИ), фактически ложно (ФЛ) и наконец, фактически неопределенно (ФН). При определении условий истинностей предложений из {Т} мы будем руководствоваться различением терминов предложений на логические(выражения естественного языка «и» , «или» , «если. . . , то. . . » , «неверно, что. . . » и т. п. ) и дескриптивные(параметры, величины, и их значения). Использование этого различения как раз и позволит нам найти критерий в оценках предложений {Т}. В зависимости от того, к смыслу логических или дескриптивных терминов мы обращаемся при установлении истинностного значения предложения, мы будем относить предложения к истинам логики или истинам факта соответственно. Теперь, упорядочим элементы множества возможных значений и покажем это в виде графа : Здесь представляет отношение <=. Видим, что наше множество частично упорядоченно.

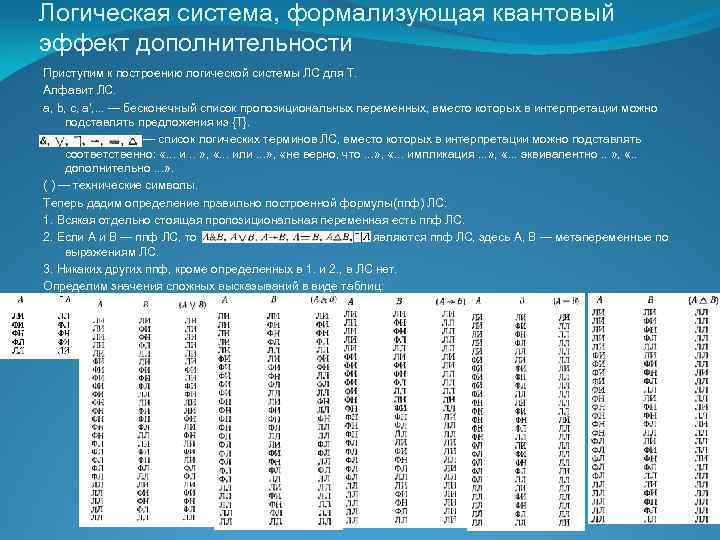Логическая система, формализующая квантовый эффект дополнительности Приступим к построению логической системы ЛС для Т. Алфавит ЛС. а, b, с, а', . . . — бесконечный список пропозициональных переменных, вместо которых в интерпретации можно подставлять предложения из {Т}. — список логических терминов ЛС, вместо которых в интерпретации можно подставлять соответственно: «. . . и. . » , «. . . или. . . » , «не верно, что. . . » , «. . . импликация. . . » , «. . . эквивалентно. . » , «. . дополнительно. . . » . ( ) — технические символы. Теперь дадим определение правильно построенной формулы(ппф) ЛС: 1. Всякая отдельно стоящая пропозициональная переменная есть ппф ЛС. 2. Если А и В — ппф ЛС, то являются ппф ЛС, здесь А, В — метапеременные по выражениям ЛС. 3. Никаких других ппф, кроме определенных в 1. и 2. , в ЛС нет. Определим значения сложных высказываний в виде таблиц:

Логическая система, формализующая квантовый эффект дополнительности Приведенные таблицы являются также средством определения тавтологий ЛС. Будем называть ппф ЛС «тавтологией» , если и только если она принимает истинностное значение ЛИ для всех возможных значений входящих в нее переменных. Отрицание тавтологии назовем "противоречием". Все остальные ппф ЛС будем называть «выполнимыми» . В качестве доказуемых формул ЛС будем рассматривать те и только те ппф ЛС, которые являются тавтологиями. Приведем список важнейших тавтологий ЛС: Нижеприведенные ппф являются лишь «выполнимыми» : формулами: Заметим, что многие важнейшие тавтологии стандартной логической системы не являются тавтологиями в ЛС. Особенно это интересно в случае «законов исключенного третьего» , «непротиворечия» , законов, выражающих парадоксы материальной импликации , дистрибутивных законов.

Логическая система, формализующая квантовый эффект дополнительности Необходимыми свойствами отношения дополнительности , так как они присущи ему в квантовомеханической теории, являются свойства антирефлексивности (ибо дополнительные высказывания обязательно являются высказываниями о значениях различных квантовомеханических величин), симметричности (ибо каждое из высказываний о значении одновременно ненаблюдаемых величин считается дополнительным к другому), и наконец, отношение дополнительности не должно обладать свойством транзитивности (что также следует из понимания дополнительности как отношения между высказываниями о значениях одновременно ненаблюдаемых величин). Исследуем свойства отношения ∆. Для этого представим его таблицу в виде матрицы: Прежде всего проверим, обладает ли отношение ∆ свой- ством рефлексивности. Для этого воспользуемся, несколько е переформулировав, теоремой из теории отношений: 1) отношение ∆ — рефлексивно, если на главной диагонали матрицы, представляющей его, стоят только ЛИ; 2) отношение ∆ — антирефлексивно, если на главной диагонали представляющей его матрицы стоят только ЛЛ. Легко видеть, что отношение ∆ антирефлексивно, ибо на главной диагонали матрицы стоят только ЛЛ. Проверим теперь это отношение на симметричность. Отношение А∆В будет симметричным, если из А∆В следует В∆А. В случае матричного представления симметричного отношения все его элементы, симметричные относительно главной диагонали, должны быть равны между собой. Легко убедиться, что это верно для нашей матрицы. Следовательно, отношение ∆ — симметрично. И наконец, исследуем отношение ∆ на транзитивность. Отношение ∆ будет транзитивным, если из того, что имеет место А∆В и В∆С, следует, что имеет место А∆С. В случае матричного представления это требование выразится следующим образом: Следовательно, отношение ∆ не является транзитивным. Таким образом, мы построили логическую систему ЛС, адекватно описывающую квантовый эффект дополнительности, основополагающий в квантовой механике.

Примеры формальных системы КЛ l l l система Гольдблатта, система Нишимуры система Катленда-Гиббинса система Хардегри система Кальмбах

Определения

Система Гольдблатта

Система Гольдблатта

Система Нишимуры

Система Нишимуры

Система Катленда-Гиббинса

Система Хардегри Стрелка Сасаки как импликация в ЛКМ

Система Г. Хардегри

Система Г. Кальмбах

Система Г. Кальмбах

Система Г. Кальмбах

Применение ЛКМ Возможные применения логики квантовой механики, прежде всего, связаны с применением образующей науки этой логики - , собственно, квантовой механики. Где бы не применялась квантовая механика, законы всех процессов невозможно полностью объяснить какой-то другой логикой. Рассмотрим некоторые примеры:

Парадокс человеческих суждений о вероятности Международная группа ученых установила [6], что квантовая механика позволяет лучше объяснить парадоксы человеческих суждений о вероятности. Людям регулярно приходится выносить суждения о вероятности того или иного события на "бытовом" уровне, то есть не пользуясь формальной логикой и теорией вероятности. Например, людям предлагается изучить следующую характеристику: Линде 31 год, она интеллектуал. Будучи студенткой она принимала участие в антивоенных демонстрациях, а также была обеспокоена проблемами дискриминации и социальной несправедливости. Затем испытуемым предлагается выбрать из двух утверждений "Линда работает банковским служащим" и "Линда работает банковским служащим и участвует в феминистском движении" более, на их взгляд, вероятное. В результате 85 процентов людей выбирают второе утверждение. При этом, с точки зрения теории, вероятность одновременной истинности двух событий не может превосходить вероятность одного из них. Этот парадокс в суждениях получил называние конъюнктивного. Распределение вероятности в случае конъюнктивного парадокса(60 экспериментов)

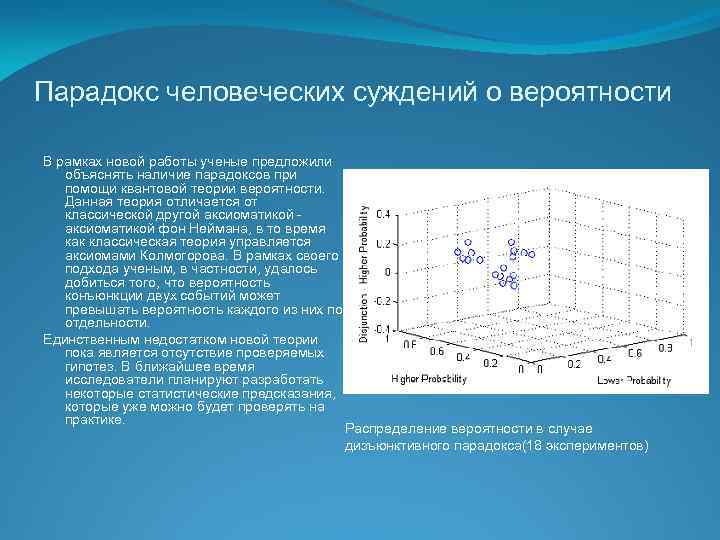Парадокс человеческих суждений о вероятности В рамках новой работы ученые предложили объяснять наличие парадоксов при помощи квантовой теории вероятности. Данная теория отличается от классической другой аксиоматикой - аксиоматикой фон Неймана, в то время как классическая теория управляется аксиомами Колмогорова. В рамках своего подхода ученым, в частности, удалось добиться того, что вероятность конъюнкции двух событий может превышать вероятность каждого из них по отдельности. Единственным недостатком новой теории пока является отсутствие проверяемых гипотез. В ближайшее время исследователи планируют разработать некоторые статистические предсказания, которые уже можно будет проверять на практике. Распределение вероятности в случае дизъюнктивного парадокса(18 экспериментов)

Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Если классический процессор в каждый момент может находиться ровно в одном из состояний , (обозначения Дирака) то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии - со своей комплексной амплитудой λj. Это квантовое состояние называется «квантовой суперпозицией» данных классических состояний и обозначается как Квантовое состояние может изменяться во времени двумя принципиально различными путями: 3 кубита квантового регистра А) Унитарная квантовая операция (квантовый вентиль против 3 битов обычного - quantum gate, ). Б) Измерение (наблюдение). Если классические состояния есть пространственные положения группы электронов в квантовых точках, управляемых внешним полем V то унитарная операция есть решение уравнения Шредингера для этого потенциала.

Квантовый компьютер Измерение есть случайная величина, принимающая значения с вероятностями | λj | 2 соответственно. В этом состоит квантово механическое правило Борна. Измерение есть единственная возможность получения информации о квантовом состоянии, так как значения λj нам непосредственно не доступны. Измерение квантового состояния не может быть сведено к унитарной шредингеровской эволюции, так как, в отличие от последней, оно необратимо. При измерении происходит так называемый коллапс волновой функции , физическая природа которого до конца не ясна. Спонтанные вредоносные измерения состояния в ходе вычисления ведут к декогерентности, то есть отклонению от унитарной эволюции, что является главным препятствием при построении квантового компьютера. Вычисление Упрощённая схема вычисления на квантовом компьютере выглядит так: берется система квантовых битов(кубитов), на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством базовых квантовых операций. В конце измеряется значение, и это результат работы компьютера. Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система дает результат, только с некоторой вероятностью являющийся правильным. Но за счет небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице. С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней Приложения к криптографии Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма RSA. Даже для самых быстрых современных компьютеров разложение числа из ста цифр на простые множители заняло бы больше бы времени, чем возраст Вселенной. Благодаря алгоритму Шора эта задача становится вполне осуществимой, если квантовый компьютер будет построен.

Применение ЛКМ в фундаментальных науках Из-за особенностей квантовой логики и самой квантовой механики, в наше время они скорее имеют большее значение для фундаментальных, чем для прикладных, наук. На мой взгляд, это направление исследований является более важным для человечества в долгосрочной перспективе. Рассмотрим влияние квантовых процессов и, соответственно, логики на космологию.

Излучение Хокинга В терминах общей теории относительности( которая, в общем, подчиняется классической логике) черные дыры из-за гравитации не выпускают даже электромагнитного излучения. Поэтому они могут лишь увеличиваться в размерах и никогда не исчезают. Излуче ние Хо кинга — процесс испускания разнообразных элементарных частиц, преимущественно фотонов, чёрной дырой. В силу закона сохранения энергии, этот процесс должен сопровождаться уменьшением массы чёрной дыры, то есть её «испарением» . Предсказан теоретически Стивеном Хокингом в 1974 году. Испарение чёрной дыры — чисто квантовый процесс. Дело в том, что понятие о чёрной дыре как объекте, который ничего не излучает, а может лишь поглощать материю, справедливо до тех пор, пока не учитываются квантовые эффекты. В квантовой же механике, благодаря туннелированию, появляется возможность преодолевать потенциальные барьеры, непреодолимые для неквантовой системы.

Излучение Хокинга В случае чёрной дыры ситуация выглядит следующим образом. В квантовой теории поля физический вакуум наполнен постоянно рождающимися и исчезающими флуктуациями различных полей (можно сказать и «виртуальными частицами» ). В поле внешних сил динамика этих флуктуаций меняется, и если силы достаточно велики, прямо из вакуума могут рождаться пары частица-античастица. Такие процессы происходят и вблизи (но всё же снаружи) горизонта событий чёрной дыры. При этом возможен случай, когда полная энергия античастицы оказывается отрицательной, а полная энергия частицы — положительной. Падая в чёрную дыру, античастица уменьшает её полную энергию покоя, а значит и массу, в то время как частица оказывается способной улететь в бесконечность. Для удалённого наблюдателя это выглядит как излучение чёрной дыры. Излучение Хокинга — главный аргумент учёных относительно распада (испарения) небольших чёрных дыр, которые теоретически могут возникнуть в ходе экспериментов на Большом Адронном Коллайдере.

Вывод Квантовая механика является одной из основополагающих теорий об устройстве нашего мира. Мы будем продолжать видеть плоды работы ученых в этой сфере. И разумеется, никакие квантовые открытия не могут быть объяснены без использования аппарата квантовой логики. С. Хокинг уже в 1974 г. смог объединить результаты ОТО и квантовой теории для построения термодинамики черных дыр(см. выше). Именно объединение результатов этих двух теорий – главная задача физиков нашего времени, ведь это приведет к созданию теории квантовой гравитации. Гениальный А. Энштейн потратил на эту задачу большую часть своей жизни, однако, не достиг успеха. Объяснение всех четырех фундаментальных взаимодействий(электромагнитного, слабое, сильное, гравитационное) в рамках квантовой теории приведет к созданию т. н. «теории всего» , полного знания человека об устройстве Вселенной. Мне остается лишь надеяться, что я стану свидетелем этого величайшего события в истории человечества.

Список литературы(с актуальными ссылками на материалы): 1. 2. 3. 4. 5. 6. Васюков В. Л Квантовая логика М. , 2005 Ивин А. А Логика М. , 1998 Меськов В. С. Очерки по логике квантовой механики М. , 1986 Печенкин А. А О природе квантовой логики http: //wikipedia. org(Квантовая Логика, Квантовый компьютер, Квантовая механика, Излучение Хокинга) Jerome R. Busemeyer, Riccardo Franco, Emmanuel M. Pothos Quantum Probability Explanations for Probability Judgment 'Errors‘