Квантовая физика Волновая функция и её статистический смысл

Квантовая физика Волновая функция и её статистический смысл. Гипотеза де Бройля. Соотношение неопределенностей Гейзенберга. Уравнение Шредингера.

Гипотеза де Бройля. • Французский ученый Луи де Бройль (1892— 1987), развивая представления о двойственной корпускулярноволновой природе света, выдвинул в 1923 году гипотезу об универсальности корпускулярно-волнового дуализма. Он утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами. • Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия и импульс , а с другой стороны — волновые характеристики — частота и длина волны.

• В 1924 Луи де Бройль выступил с гипотезой о том, что корпускулярно-волновой дуализм присущ всем без исключения видам материи — электронам, протонам, атомам и т. д. , причём количественные соотношения между волновыми и корпускулярными свойствами частиц те же, что и установленные ранее для фотонов. • А именно, если частица имеет энергию E и импульс p, то с ней связана волна, частота которой υ = E/h и длина волны λ = h/p, где h = 6· 10 -34 Дж·сек — постоянная Планка. • Для частиц не очень высокой энергии λ = h/mv, где m и v — масса и скорость частицы. Таким образом, длина волн де Бройля тем меньше, чем больше масса частицы и её скорость. • Например, частице массой в 1 г, движущейся со скоростью 1 м/сек, будет соответствовать длина волны де Бройля с λ = 10 -18 Å, что лежит за пределами доступной наблюдению области.

Волновая функция и ее статистический смысл • Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, а также противоречие целого ряда экспериментов с применяемыми в начале XX в. теориями привели к новому этапу развития квантовой теории — созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. • Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20 -х годов XX в. ; оно связано прежде всего с работами австрийского физика Э. Шредингера (1887— 1961), немецкого физика В. Гейзенберга и английского физика П. Дирака (1902— 1984). Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории.

• Волнова я фу нкция (функция состояния, пси-функция, амплитуда вероятности) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы, имеющей протяжённость в пространстве. В широком смысле — то же самое, что и вектор состояния.

• Описание состояния микрообъекта с помощью волновой функции имеет статистический, т. е. вероятностный характер: квадрат абсолютного значения (модуля) функции указывает значение вероятностей тех величин, от которых она зависит. • Например, если задана зависимость волновой функции частицы от координат х, у, z и времени t, то квадрат модуля этой функции определяет вероятность обнаружить частицу в момент t в точке с координатами х, у, z. Поскольку вероятность состояния определяется квадратом волновой функции, её называют также амплитудой вероятности.

Волновая функция одновременно отражает и наличие волновых свойств у микрообъектов. • Так, для свободной частицы с заданным импульсом р и энергией E, которой сопоставляется волна де Бройля с частотой υ = E/h и длиной волны λ = h/p (где h — постоянная Планка), волновая функция должна быть периодична в пространстве и времени с соответствующей величиной λ и периодом Т = 1/υ. • Для волновой функции справедлив принцип суперпозиций: если система может находиться в различных состояниях с псифункцией ψ1, ψ2. . , то возможно и состояние с пси-функцией, равной сумме (и вообще любой линейной комбинации) этих функций. Сложение пси-функций (амплитуд вероятностей), а не вероятностей (квадратов функции) принципиально отличает квантовую теорию от любой классической статистической теории (в которой справедлива теорема сложения вероятностей).

Клинтон Дэвиссон (слева) и Лестер Джермер (справа).

Опыт Дэвиссона и Джермера. Параллельный пучок электронов, создаваемый «электронной пушкой» А, направлялся на монокристалл никеля. Коллектор мог устанавливаться под любым углом Θ относительно падающего пучка, вращая его все время в одной плоскости. По показанию гальванометра можно было судить об интенсивности пучков электронов, рассеянных в различных направлениях. Измерения силы тока при разных положениях коллектора позволило получить представление об интенсивности отражения электронов в различных направлениях. Схема опыта Дэвиссона — Джермера: К — монокристалл никеля; А — источник электронов; В — приёмник электронов; θ— угол отклонения электронных пучков. Пучок электронов падает перпендикулярно отшлифованной плоскости кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы.

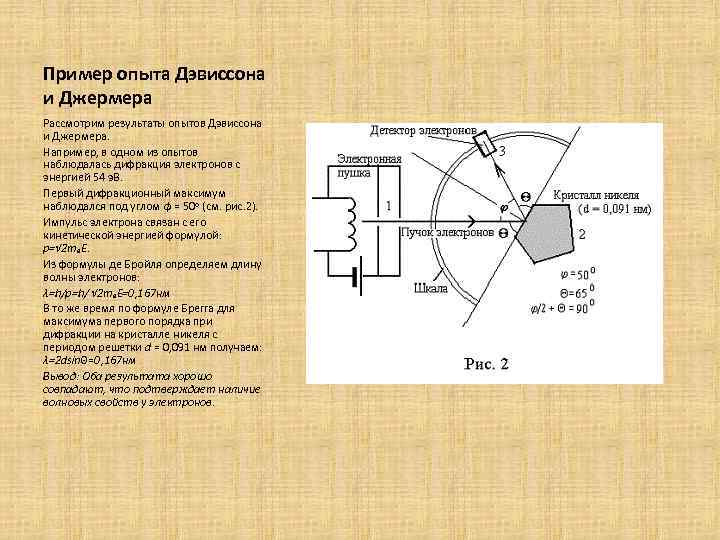Пример опыта Дэвиссона и Джермера Рассмотрим результаты опытов Дэвиссона и Джермера. Например, в одном из опытов наблюдалась дифракция электронов с энергией 54 э. В. Первый дифракционный максимум наблюдался под углом ϕ = 50 о (см. рис. 2). Импульс электрона связан с его кинетической энергией формулой: p=√ 2 mₑE. Из формулы де Бройля определяем длину волны электронов: λ=h/p=h/ √ 2 mₑE=0, 167 нм В то же время по формуле Брегга для максимума первого порядка при дифракции на кристалле никеля с периодом решетки d = 0, 091 нм получаем: λ=2 dsinΘ=0, 167 нм Вывод: Оба результата хорошо совпадают, что подтверждает наличие волновых свойств у электронов.

Вернер Гейзенберг

Соотношение неопределенностей Гейзенберга • Принцип неопределённости Гейзенбе рга в квантовой механике — принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы и нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. • Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г. , является одним из краеугольных камней квантовой механики. Согласно принципу неопределённостей, частица не может быть описана как классическая частица, то есть например у нее не могут быть одновременно точно измерено положение и скорость. • Пример: частица с определённым значением энергии, находящаяся в коробке с идеально отражающими стенками; она не характеризуется ни каким-либо определённым «положением» или пространственной координатой, ни определённым значением импульса.

Принцип неопределенности заключается в принципиальной невозможности одновременно точно определить положение микрочастицы в пространстве и ее импульс: • Δpx · Δ x ≥ h / 2π, • где Δpx = m Δvxx - неопределенность (ошибка в определении) импульса микрообъекта по координате х; Δx - неопределенность (ошибка в определении) положения микрообъекта по этой координате. • Таким образом, чем точнее определена скорость, тем меньше известно о местоположении частицы, и наоборот. Поэтому для микрочастицы становится неприемлемым понятие о траектории движения, поскольку оно связано с конкретными координатами и импульсом частицы. Можно лишь говорить о вероятности обнаружить ее какой-то областях пространства.

• Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей: ∆ε ∆t ≥ ħ • Если под неопределённостями координаты и импульса понимать среднеквадратичные отклонения этих физических величин от их средних значений, то принцип неопределённости для них имеет вид: ∆px ∆x ≥ ħ/2, ∆py ∆y ≥ ħ/2, ∆pz ∆z ≥ ħ/2

Эрвин Шрёдингер — один из основоположников квантовой механики.

Уравнение Шрёдингера • Уравнение, описывающее изменение в пространстве и во времени состояния, задаваемого волновой функцией, в квантовых системах. • Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике. Его можно назвать уравнением движения квантовой частицы. • Установлено Эрвином Шрёдингером в 1926 году. • Уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света. В случае быстрых частиц и частиц со спином используются его обобщения ( уравнение Паули, уравнение Дирака и др. ). • Открытие уравнения Шрёдингера последовало за революционным предположением де Бройля, что не только свету, но и вообще любым телам (в том числе и любым микрочастицам) присущи волновые свойства.

Основное уравнение Шредингера. Это уравнение позволяет найти волновую функцию ψ(x, y, z, t) как функцию координат и времени, определить плотность вероятности нахождения частицы в любой точке пространства в любой момент времени и тем самым полностью описать квантовое состояние частицы, движущейся в силовом поле. Где: -- оператор полной энергии частицы (оператор Гамильтона) Стационарное уравнение Шредингера. где оператор Лапласа. Его решения – функции и соответствующие значения энергии Е - определяются конкретным видом потенциальной энергии частицы . Часто уравнение Шредингера для стационарных состояний записывают в следующей форме:

Волновое уравнение было предложено в 1926 г. немецким физиком Э. Шрёдингером (1887 -1961) для описания состояния электрона в атоме водорода. Он объединил математические выражения для колебательных процессов и уравнение де Бройля: где ψ - волновая функция (аналог амплитуды для волнового движения), характеризующая движение электрона в пространстве как волнообразное возмущение; x, y, z - координаты, m - масса покоя электрона, h - постоянная Планка, E - полная энергия электрона, Ep - потенциальная энергия электрона.

• Решениями уравнения Шрёдингера являются волновые функции. Для одноэлектронной системы (атома водорода) выражение для потенциальной энергии электрона имеет простой вид: • Ep = −e 2 / r, • где e - заряд электрона, r - расстояние от электрона до ядра. • В этом случае уравнение Шрёдингера имеет точное решение.