Кванторные операции Продолжение Отрицание предложений с кванторами

Кванторные операции Продолжение

Отрицание предложений с кванторами. Известно, что часто для отрицания некоторого предложения достаточно предпослать сказуемому этого предложения отрицательную частицу “не”. Например, отрицанием предложения “Река х впадает в Черное море. ” является предложение “ Река х не впадает в Черное море ”. Годится ли этот прием для построения отрицаний предложений с кванторами?

• Сравните высказывания: “Все птицы летают ” и “Все птицы не летают”. • Эти высказывания не являются отрицаниями друга, т. к. они оба ложны. Или • “ Некоторые птицы летают ” и “ Некоторые птицы не летают ”. • И эти высказывания не являются отрицанием друга, т. к. они оба истинны.

• Таким образом , добавление частицы “не” к сказуемому в предложениях , содержащих кванторы (“Все х суть Р” и “Некоторые х суть Р” ) не образуют отрицания этих высказываний.

• Универсальным способом построения отрицания данного высказывания является добавление словосочетания “наверно, что” в начале предложения.

• Таким образом, отрицанием высказывания “Все птицы летают” является предложение “Неверно, что все птицы летают”; но это предложение имеет тот же смысл, что и предложение “Некоторые птицы не летают”.

• По аналогии, отрицанием высказывания “Некоторые птицы летают” является высказывание “Неверно, что некоторые птицы летают”, которое имеет тот же смысл, что и предложение “Все птицы не летают”.

• Условимся отрицание предложения записывать как , а отрицание предложения – как .

• Иначе говоря, для того, чтобы построить отрицание предиката, связанного квантором общности нужно квантор общности заменить на квантор существования, а предикат на его отрицание.

• F(x) : всякая конфета шоколадная. • : найдется конфета не шоколадная.

• Для того, чтобы построить отрицание предиката, связанного квантором существования нужно квантор существования заменить на квантор общности, а предикат на его отрицание.

• В(х): существуют реки, впадающие в озера. • : любая река не впадает в озеро.

Отрицание сложных высказываний (законы де Моргана) • Рассмотрим сложное высказывание: • Число 9 – простое и кратно 3. • Это высказывание представляет конъюнкцию двух простых высказываний. (А Λ В). • Это высказывание ложно.

• Как сформулировать отрицание этого высказыания? • Можно …. • 1. • 2.

• 1. С помощью слов «неверно, что…» • 2. С помощью частицы «не» перед сказуемым.

• 1. Неверно, что число 12 -простое и кратно 3. • Это высказывание также ложно. • 2. Число 12 не является четным и кратным 3. • И это высказывание ложно. • Следовательно для построения отрицания ни 1 , ни 2 способ не подходят

Огастес (Август) де Мо рган (англ. Augustus de Morgan, 27 июня 1806, Мадура, Индия — 8 марта 1871, Лондон) — шотландский математик и логик; профессор математики в Университетском колледже Лондона (1828— 1831, 1836— 1866). Первый президент (1866) Лондонского математического общества. Основные труды: по математической логике и теории рядов; к своим идеям в алгебре логики пришёл независимо от Дж. Буля. Изложил (1847) элементы логики высказываний и логики классов, дал первую развитую систему алгебры отношений. С его именем связаны известные теоретико-множественные соотношения (законы де Моргана)

• Первый закон Де Моргана • Отрицанием конъюнкции двух высказываний А и В является дизъюнкция их отрицаний.

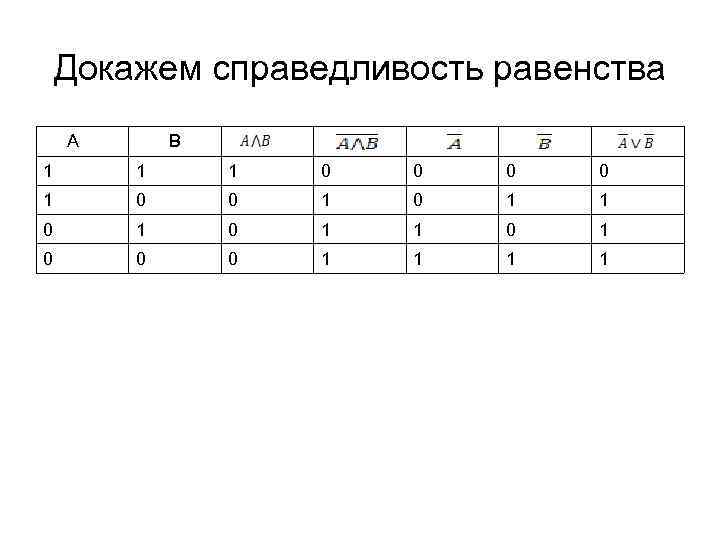Докажем справедливость равенства Aa A B 1 1 1 0 0 1 0 1 0 0 0 1 1 B

• Второй закон де Моргана • Отрицанием дизъюнкции высказываний • A и B является конъюнкция их отрицаний.

• Ответ на поставленный вопрос будет таким: • Число 12 – не простое или не кратно 3

• 3 форма мышления умозаключение

• Умозаключение – это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение. • Существование такой формы в нашем мышлении обусловлено самой объективной действительностью. • Вместе с понятиями и суждениями умозаключения преодолевают ограниченность чувственного познания.

• Умозаключения оказываются незаменимыми там, где органы чувств бессильны: в постижении причин и условий возникновения какого-либо предмета или явления, его сущности и форм существования, закономерностей развития. • Умозаключения участвуют в образовании понятий и суждений, которые нередко выступают как итог умозаключений, чтобы стать средством дальнейшего познания.

• Под рассуждением или умозаключением будем понимать логическую операцию, посредством которой из одного или нескольких высказываний (посылок), формулируется новое по отношению к исходным заключение.

• В словесных формулировках заключение отделяется от посылок с помощью слов «следовательно» , «значит» … • Для удобства договорились записывать умозаключение с посылками А 1 и А 2 и заключением В в виде Черта в данной записи заменяет слово следовательно.

• • • Например: А 1: 1∙ 2=1+1=2 А 2: 1∙ 3=1+1+1=3 А 3: 1∙ 4=1+1+1+1=4, следовательно 1∙а=а. Умозаключение построено путем рассуждения от частного к общему.

• Пример 2. При обосновании выбора действий при решении уравнения х+5=12 • А 1: Для нахождения неизвестного слагаемого нужно от суммы вычесть известное слагаемое. • А 2: В уравнении х+5=12 не известно первое слагаемое. Заключение: х=12 -5. х=7 Рассуждение проведено от общего к частному.

• Умозаключения бывают самые разные. В одних идем от частного к общему, в других от общего к частному. • В основе классификации умозаключений, лежит отношение логического следования. Умозаключения Дедуктивные Недедуктивные

• Дедуктивными называют умозаключения, в которых между посылками и заключением имеет место отношение логического следования. • Недедуктивными называют умозаключения, в которых нет логического следования между посылками и заключением.

• Примерами дедуктивных рассуждений могут быть: • Умозаключение, сформулированное на основе применения в решении доказанной теоремы. • Умозаключение, сформулированное на основе общепризнанного факта (аксиомы)

• Схемы , наиболее часто встречающихся дедуктивных умозаключений. В математике такие схемы называются правилами вывода. • 1. правило заключения. • 2 правило отрицания. • 3. правило силлогизма.

• Например: Если треугольник равнобедренный, то углы при основании равны. Треугольник АВС – равнобедренный. Следовательно, в треугольнике АВС углы при основании равны. • Логическая структура умозаключения будет иметь вид:

• Еще один пример. Если треугольник равнобедренный, то углы при основании равны. В треугольнике MNP углы при его основании не равны, следовательно, треугольник MNP не равнобедренный. • Логическая структура этого умозаключения имеет вид:

• Примерами недедукивных рассуждений могут быть: • Рассуждения на основе неполной индукции. • Рассуждения на основе полной индукции (метод математической индукции). • Рассуждения по аналогии.

Неполная индукция • Определение. Умозаключение называется индуктивным, если на основании того, что некоторые объекты класса обладают определенным свойством, делается вывод, что этим свойством обладают все объекты данного класса.

• • • Например: 1+2=2+1 3+5=5+3 7+9=9+7 14+27=27+14 Следовательно, от перемены мест слагаемых сумма не меняется.

• Но! • • 3+5<3∙ 5 2+7<2∙ 7 4+8<4∙ 8 Следовательно, сумма двух натуральных чисел больше их произведения. • Но! 4+1 > 4∙ 1.

• На основе индкутивных рассуждений можно сформулировать гипотезу, которую необходимо доказать или опровергнуть.

Метод математической индукции • Метод математической индукции основан на аксиоме 4 Дж. Пиано. • Аксиома 4. • Пусть множество M есть подмножество множества N и известно, что • 1. единица содержится в M; • 2. из того, что a содержится в M, следует, что и a′ содержится в M. • Тогда множество M совпадает со множеством N.

• Метод математической индукции является строгим доказательством. • Он состоит из трех этапов: • 1. проверки справедливости высказывания для n=1 • 2. выдвижения гипотезы (предположения) о справедливости высказывания для n=k

• Доказать, что 1+2+3+4…n= Выберем множество M, для элементов которого данное равенство верно. 1. n=1 1=1, так как 2. n=2 1+2=3, так как Следовательно, 1 принадлежит M

• 2. Предположим, что равенство верно для всех k

• Доказательство. Выделим первые k слагаемых и заменим их суммой. • (1+2+3+4+…+k)+(k+1)= • = ч. т. д. Вывод: данное равенство верно на множестве N чисел.

Теорема. Структура теоремы. Виды теорем • Любое понятие характеризуется объемом и содержанием. Часть существенных свойств отражаются в определении понятия. • Другая часть свойств формулируется в виде умозаключения (логического следования) с квантором общности или существования. • Такие умозаключения мы называем теоремами.

• Например: • В любом равнобедренном треугольнике углы при основании равны.

• В любой теореме можно выделить условие, заключение и разъяснительную часть. • Эти три компонента составляют структуру теоремы.

• С логической точки зрения теорема есть высказывание , А – условие, Взаключение. Разъяснительная часть обычно явно не присутствует в формулировке теореме, но всегда подразумевается.

• • • Например: теорема. Если углы вертикальные, то они равны. Условие: углы вертикальные. Заключение: вертикальные равны. Разъяснительная часть множество вертикальных углов, образованных при пересечении прямых.

Виды теорем • • Прямая теорема Обратная теорема Противоположная теорема Теорема, обратная противоположной.

• Если углы вертикальные, то они равны. (прямая теорема) • Если углы равны, то они вертикальные. • (обратная теорема) • Если углы не вертикальные, то они не равны. (противоположная теорема) • Если углы не равны, то они не вертикальные. (обратная противоположной).

Закон контрапозиции • Прямая теорема и теорема, обратная противоположной, истинны одновременно. • Символичная запись данного закона имеет вид:

Спасибо за внимание!