КВАЛІФІКАЦІЙНА РОБОТА МАГІСТРА Розробка та дослідження методів оптимального синтезу складних гідравлічних мереж для різних видів початкового завдання потокорозподілу Виконала: студентка 5 курсу групи МТз-271 спеціальності 8. 04030101 «Прикладна математика» Бєда Оксана Василівна Науковий керівник: доцент кафедри прикладної математики, кандидат технічних наук Малий Вячеслав Вадимович 1
n. Мета дипломної роботи Здійснити: • а) аналіз стану проблеми моделювання процесу потокорозподілу у складних гідравлічних мережах кільцевого типу; • б) розробку математичної моделі складної гідравлічної мережі та побудову на її основі методів і алгоритмів розрахунку певних режимів її функціонування; • в) побудову методів та алгоритмів оптимального синтезу елементів системи регулюючих органів складних гідравлічних мереж для різних видів завдання початкового потокорозподілу. 2
РОЗДІЛ 1. ДОСЛІДЖЕННЯ МЕТОДІВ МОДЕЛЮВАННЯ ПОТОКОРОЗПОДІЛУ У СКЛАДНИХ ГІДРАВЛІЧНИХ МЕРЕЖАХ 3
4
5
РОЗДІЛ 2. МЕТОДИ ОПТИМАЛЬНОГО СИНТЕЗУ ГІДРАВЛІЧНИХ МЕРЕЖ ПРИ ПОВНІСТЮ ЗАДАНОМУ ПОТОКОРОЗПОДІЛУ 6
7
РОЗДІЛ 3. Розробка загального диференціального алгоритму оптимального синтезу гідравлічної мережі 8
9
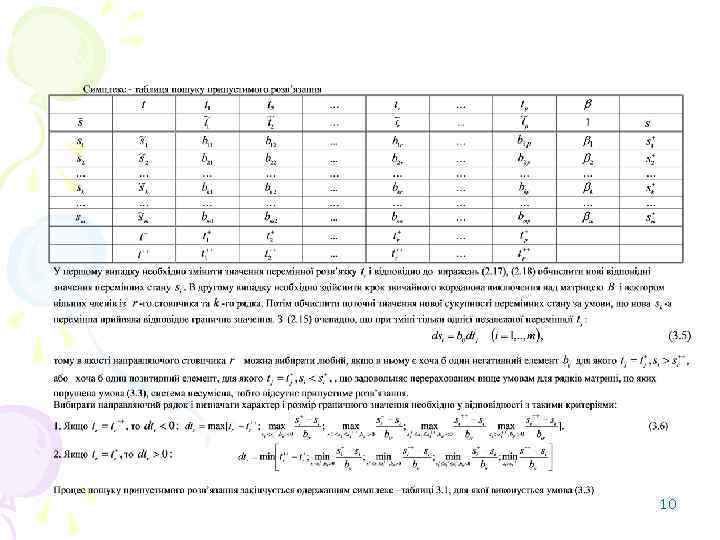
10
РОЗДІЛ 4. ОПТИМАЛЬНИЙ СИНТЕЗ ГІДРАВЛІЧНОЇ МЕРЕЖІ ПРИ ЧАСТКОВО ЗАДАНОМУ ПОТОКОРОЗПОДІЛУ 11
12
Висновки 1. Досліджена математична модель сталих процесів потокорозподілу в гідравлічних мережах при матричному й обліковому представленні елементів графа мережі і дослідження розв’язання задач аналізу. Показано, при яких умовах пряма задача аналізу має єдине розв’язання, і розглянутий загальний підхід до розв’язання нелінійних рівнянь математичної моделі щодо незалежних перемінних і параметрів, число яких дорівнює числу рівнянь. 2. Приведено математичні постановки двох оптимальних задач на гідравлічних мережах: задачі оптимізації параметрів гілок гідравлічних мереж за критерієм вартості чи ваги при системному синтезі і задачі синтезу оптимальної по енерговитратах системи регулювальних органів стосовно до СГМ. Показано, що друга з них є задачею математичного програмування при обмеженнях у виді рівностей і двосторонньої обмеженості перемінних, а перша зводиться до задачі математичного програмування того ж виду. 13
3. Приведено необхідні і достатні умови для точки мінімуму задачі математичного програмування при обмеженнях у виді рівностей і двосторонньої обмеженості перемінних, розвитий загальний підхід для її розв’язання. 4. Досліджено і розв’язана задача оптимізації параметрів гілок гідравлічної мережі за критерієм ваги чи вартості при цілком і частково заданому потокорозподілу. Для обох модифікацій отримано необхідні і достатні умови для точки мінімуму і розроблені алгоритми розв’язання в загальному виді і їхній деталізації стосовно кільцевим водопровідним мережам. 5. Розроблені алгоритми розв’язання поставлених задач та приведена їх програмна реалізація. Крім того, з метою поліпшення якості функціонування цих алгоритмів розглянуті додаткові заходи, які стосуються спеціальних форм представлення топологічної інформації та раціонального вибору дерев із екстремальними характеристиками. 14
Скачать презентацию КВАЛІФІКАЦІЙНА РОБОТА МАГІСТРА Розробка та дослідження методів оптимального
Презентация Беда-магистр МТз-271.ppt