Курсовой проект по дисциплине Идентификация и диагностика систем

Курсовой проект по дисциплине «Идентификация и диагностика систем» по теме: ИССЛЕДОВАНИЕ ЗАМКНУТОГО ОБЪЕКТА ИДЕНТИФИКАЦИИ С ЗАПАЗДЫВАНИЕМ Выполнил: Орлов В. О. , гр. ЭТМО-31 Руководитель: Тарасова Г. И.

Задачи курсового проекта: 1. Идентификация термического объекта по переходной характеристике и оценка адекватности математической модели. 2. Анализ устойчивости и качества замкнутой САУ с помощью частотного метода. 3. Расчет переходных характеристик с помощью компьютерного моделирования и оценка качества переходного процесса. 4. Оценка влияния запаздывания на величину Ккр по асимптотическим ЛЧХ. 5. Расчет переходных характеристик замкнутой САУ с учетом запаздывания.

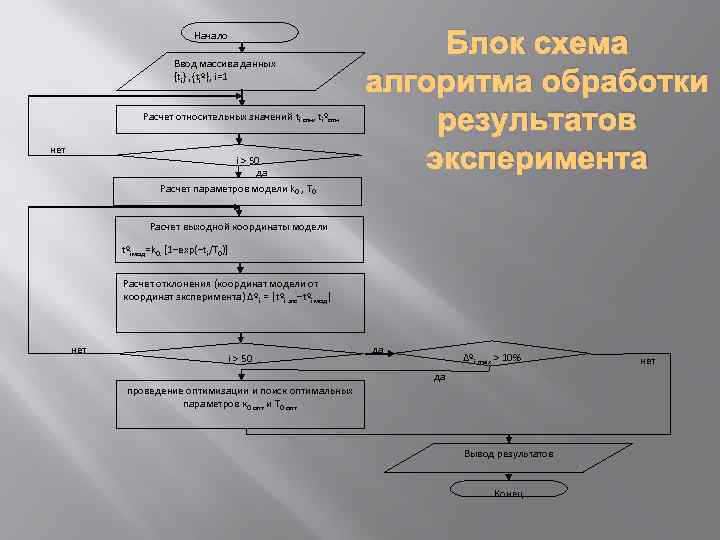Начало Ввод массива данных {ti}, {tiº}, i=1 Расчет относительных значений ti отн, tiºотн нет i > 50 да Расчет параметров модели k 0 , Т 0 Блок схема алгоритма обработки результатов эксперимента Расчет выходной координаты модели tºiмод=k 0. [1−exp(−ti/T 0)] Расчет отклонения (координат модели от координат эксперимента) ∆ºi = │tºi экс−tºi мод│ нет i > 50 да ∆ºi max > 10% да проведение оптимизации и поиск оптимальных параметров к 0 опт и Т 0 опт Вывод результатов Конец нет

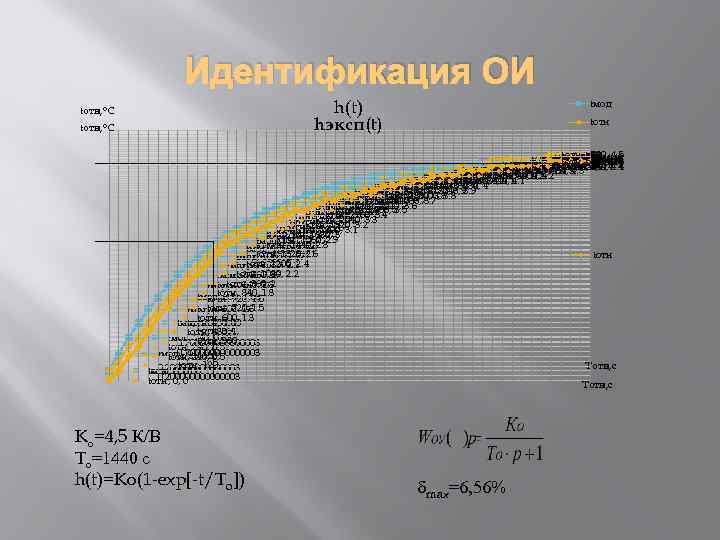Идентификация ОИ h(t) hэксп(t) tотн, °С tмод tотн 5880, 5760, 5640, 5520, 5400, 5880, tмод, 5520, 4. 42 5760, tотн, tмод, 5280, 4. 39 tотн, 5040, 4. 4 tотн, 5400, 4. 41 4680, 5640, 4. 36 tотн, 4. 44. 34 4. 5 5280, 5040, tотн, 5160, 4. 5 5880, 5760, 5640, 5520, 5400, tмод, 4800, 4. 40 4800, tотн, 4. 2 4440, 4680, 5160, 4. 38 tотн, 4. 2 tмод, 4920, 4. 4 tмод, 4320, 4560, 4920, 4. 37 tмод, 4200, 4440, tотн, 4. 33 4. 35 tмод, 4080, 4320, 4. 34. 29 4. 4 4080, tмод, 4680, tмод, 4. 13 tмод, 4. 24 tотн, 4. 3 5040, 4. 4 3960, tмод, 4560, 4. 31 tотн, 4. 16 tотн, 4. 28 4. 3 5160, tотн, 4. 19 tотн, 4. 3 4800, 4. 4 tотн, 4. 14. 21 tотн, 4. 3 4920, 3960, 4200, 4. 26 4. 3 5280, tмод, 4. 10 tмод, 4. 06 tотн, 4320, 3720, tотн, 4440, tмод, 3600, 3840, tотн, 4. 2 4560, 3600, tотн, 4200, 4. 2 tотн, 4. 03 43840, tотн, tмод, 3480, tотн, 4080, 3480, tмод, 3360, tотн, 3960, 4. 2 3360, 43720, tмод, 3240, 3600, tотн, 3. 94 tмод, 3120, 3. 98 tмод, 3000, tотн, 3. 9 3840, 4. 1 tотн, 4. 1 tотн, 3240, tмод, 2880, 3120, tотн, 3720, 4. 1 2880, 3. 89 tмод, 2760, tотн, 3. 8 3480, tотн, 3. 72 3. 84 3. 9 tотн, 3. 78 tотн, 3000, tмод, 2640, tотн, 3. 8 3360, 4 4 2640, 3. 7 3120, 3. 9 tмод, 2520, tотн, 3. 7 3240, 3. 9 tотн, 3. 65 tотн, 2760, tмод, 2400, tотн, 2520, 2880, 3. 8 tмод, 2280, tотн, 3. 6 3000, 3. 8 tотн, 2640, tотн, 2280, 3. 58 tотн, 2400, 2760, 3. 7 tмод, 2160, tотн, 3. 5 3. 7 tотн, 3. 50 tмод, 2040, 3. 41 3. 5 3. 6 tотн, 2160, 3. 4 3. 5 tотн, 2280, tотн, 2520, tмод, 1920, 3. 31 3. 4 tотн, 2040, 2400, tотн, 2160, 3. 5 tмод, 1800, 3. 21 3. 3 tотн, 1920, 3. 2 tотн, 3. 10 3. 2 2040, 3. 3 tотн, 1800, tмод, 1680, 3 3. 1 tотн, 1920, tотн, 1680, tмод, 1560, 2. 9 tотн, 1800, tотн, 1560, 2. 98 tмод, 1440, 2. 8 3 3. 1 tотн, 1680, tотн, 1440, 2. 84 tотн, 1560, 2. 9 tмод, 1320, 2. 6 tотн, 1440, tотн, 1320, 2. 70 tмод, 1200, 2. 54 2. 8 tотн, 1320, tотн, 1200, 2. 4 tмод, 1080, 2. 37 2. 6 tотн, 2. 19 tотн, 1080, 2. 2 tмод, 960, 1200, 2. 4 tотн, 1. 99 tотн, 960, 2 tмод, 840, 1080, 2. 2 tотн, 1. 77 tотн, 840, 1. 8 tмод, 720, 960, 2 tотн, 1. 53 tмод, 600, 840, 1. 8 tотн, 720, 1. 5 tотн, 600, 1. 3 tмод, 480, 1. 28 tотн, 600, 1. 3 tотн, 480, 1 tмод, 360, 1. 00 tотн, 360, tотн, 480, 1 tмод, 240, 0. 69 tотн, 360, 0. 700000003 tотн, 240, 0. 5 0. 700000003 tмод, 120, tотн, 0. 36 tотн, 240, 0. 5 tотн, 120, Tотн, с 0. 200000003 tмод, 0, 0 tотн, 0, 0. 00 0. 200000003 tотн, 0, 0 Tотн, с Kо=4, 5 К/В Tо=1440 с h(t)=Ko(1 -exp[-t/To]) δmax=6, 56%

Передаточная функция САУ Передаточная функция разомкнутой системы регулирования для П–закона имеет вид: Передаточная функция такой замкнутой системы имеет вид: Структурная математическая модель непрерывной системы управления термическим оборудованием с П законом регулирования.

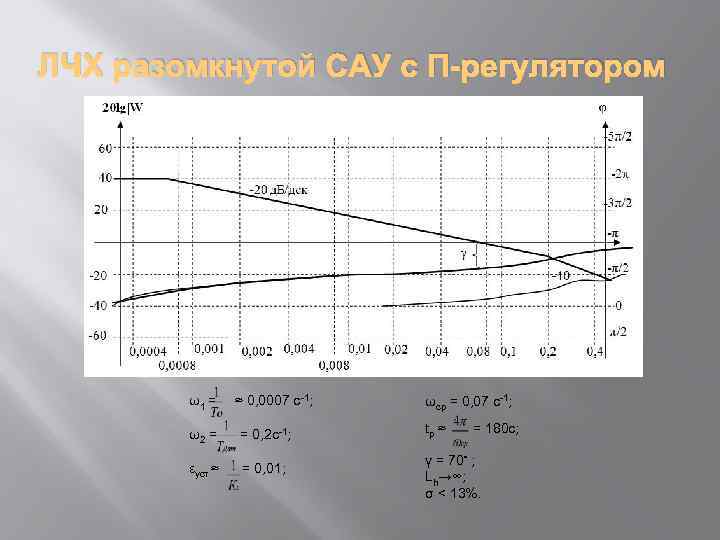ЛЧХ разомкнутой САУ с П-регулятором ω1 = ≈ 0, 0007 с-1; ω2 = = 0, 2 с-1; εуст ≈ = 0, 01; ωср = 0, 07 с-1; tp ≈ = 180 с; γ = 70◦ ; Lh→∞; σ < 13%.

Компьютерное моделирование и расчет переходных процессов САУ Схема моделирования системы управления термическим оборудованием с П законом.

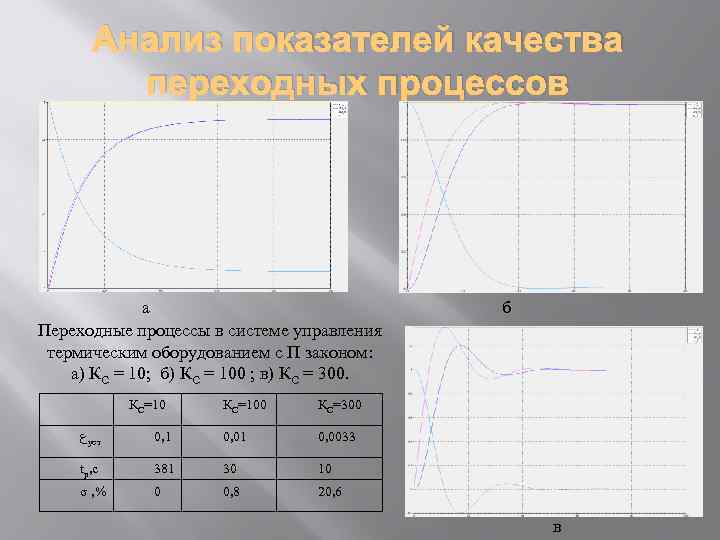Анализ показателей качества переходных процессов а Переходные процессы в системе управления термическим оборудованием с П законом: а) КС = 10; б) КС = 100 ; в) КС = 300. КС=100 б КС=300 ﻉ уст 0, 1 0, 0033 tp, c 381 30 10 σ , % 0 0, 8 20, 6 в

Передаточная функция САУ с запаздыванием ; Структурная математическая модель непрерывной системы управления термическим оборудованием с запаздыванием с П законом регулирования. Wраз (р) = =

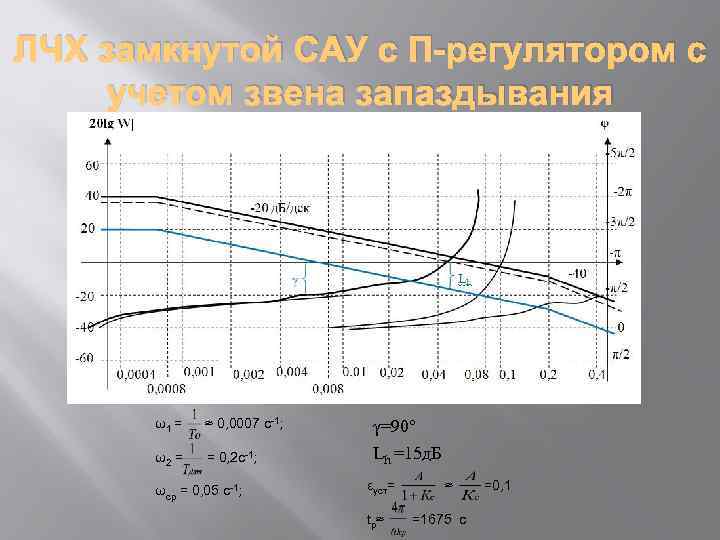ЛЧХ замкнутой САУ с П-регулятором с учетом звена запаздывания ω1 = ≈ 0, 0007 с-1; γ=90° ω2 = = 0, 2 с-1; Lh =15 д. Б ωср = 0, 05 с-1; εуст= tp≈ ≈ =1675 с =0, 1

Компьютерное моделирование САУ с запаздыванием Схема моделирования САУ термическим объектом с Прегулятором при учете запаздывания.

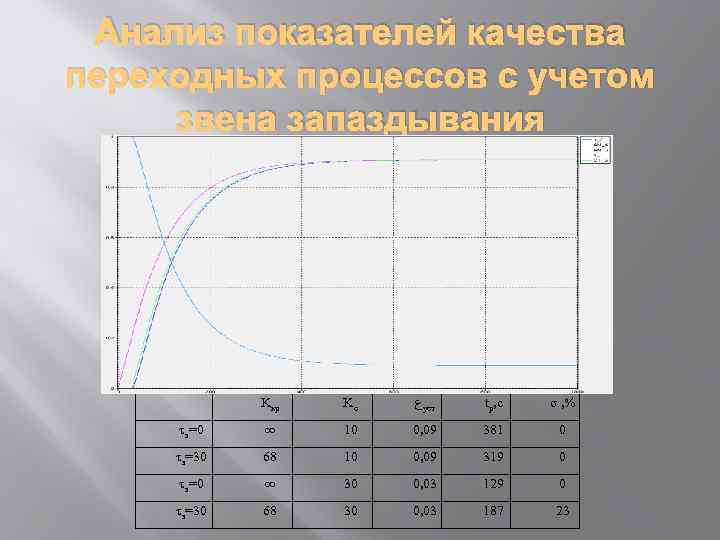Анализ показателей качества переходных процессов с учетом звена запаздывания Kкр Kc ﻉ уст tp, c σ , % τз=0 ∞ 10 0, 09 381 0 τз=30 68 10 0, 09 319 0 τз=0 ∞ 30 0, 03 129 0 τз=30 68 30 0, 03 187 23

Основные результаты и выводы В результате идентификации термического объекта по временной характеристике получено математическое описание объекта управления в виде типового апериодического звена, оценены его параметры: КО=4, 5 К/В; ТО=1440 с. Получены оценки запасов устойчивости и показателей качества замкнутой САУ с исследуемым термическим объектом по ЛЧХ разомкнутой системы при заданном законе регулирования. Проведено компьютерное моделирование исследуемой САУ с заданным законом регулирования, рассчитаны переходные процессы и оценено их качество. Проведено исследование САУ с учетом запаздывания термического объекта. Показано, что звено запаздывания оказывает негативное влияние на показатели устойчивости системы и качества переходного процесса, что необходимо учитывать при анализе и синтезе САУ с термическим объектом. Однако при небольших коэффициентах усиления, звено запаздывания может положительно сказаться за качестве переходного процесса.