Курсовая работа Гамильтонов графы Гамильтонов граф

Курсовая работа Гамильтонов графы

Гамильтонов граф • В 1857 году ирландский математик Гамильтон предложил игру «Путешествие по додекаэдру» . Игра сводилась к обходу по ребрам всех вершин правильного додекаэдра (Рис. 1), при условии, что ни в одну из вершин нельзя заходить более одного раза. • Додекаэдр – это многогранник, гранями которого служат 12 правильных пятиугольников. У него 20 вершин и 30 ребер. На Рис. 1 изображен додекаэдр с прозрачными гранями, на Рис. 2 додекаэдр с непрозрачными гранями. В каждой его вершине сходятся по три ребра.

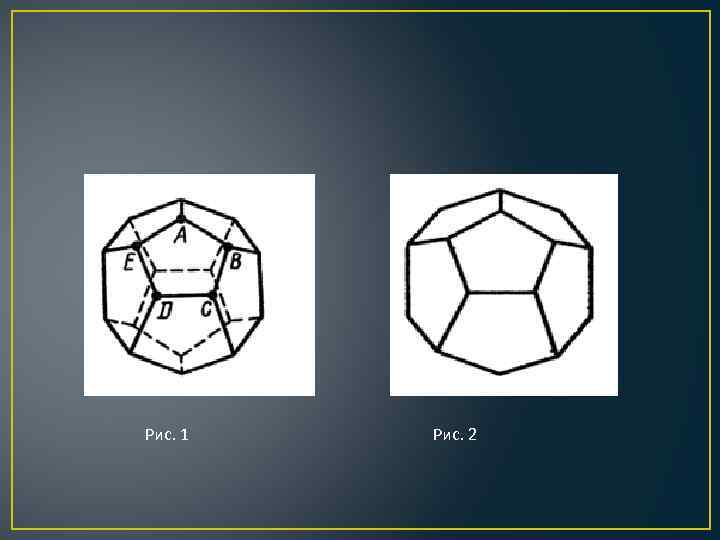
Рис. 1 Рис. 2

• Вершины и ребра додекаэдра составляют некоторый плоский граф. Плоское его представление можно получить следующим образом. Пусть ребра проволочного додекаэдра можно растягивать без разрывов. Взявшись за вершины A, B, C, D, E, растянем «каркас» додекаэдра на плоскости так, чтобы не появилось новых точек пересечения ребер (Рис. 3). Плоское представление готово. Рис. 3

• Задача. Найдите цикл, содержащий все вершины додекаэдра, причем в точности по одному разу каждую. Для определенности начните путь из вершины 1 и в первую очередь посетите вершины 2, 3, 4 и 5 (Рис. 4). Рис. 4

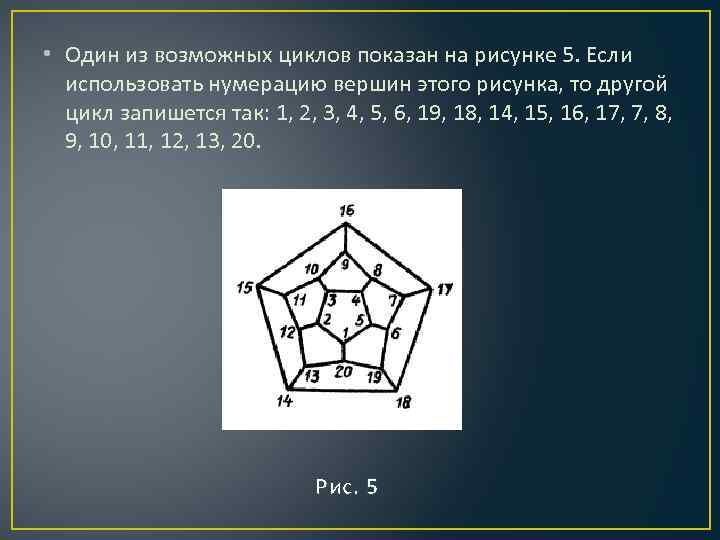
• Один из возможных циклов показан на рисунке 5. Если использовать нумерацию вершин этого рисунка, то другой цикл запишется так: 1, 2, 3, 4, 5, 6, 19, 18, 14, 15, 16, 17, 7, 8, 9, 10, 11, 12, 13, 20. Рис. 5

• Гамильтоновым циклом (путем) в графе называется цикл (путь), проходящий через каждую вершину графа в точности по одному разу. • Гамильтоновым путем в графе называется путь, проходящий через каждую вершину графа в точности по одному разу. Гамильтонов путь (цикл) всегда является простым. Он может не содержать всех ребер графа. • Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.

Теорема Дирака ( 1952) • Если в простом графе с n ≥ 3 вершинами p(v) ≥ n/2 для любой вершины v, то граф G является гамильтоновым.

Упражнения 1. Торговец, живущий в городе А 1, собирается посетить города А 2, А 3, А 4. Расстояния между городами таковы: А 1 А 2 = 120, А 1 А 3 = 140, А 1 А 4 =180, А 2 А 3 = 70, А 2 А 4 = 100, А 2 А 4 = 110. Найти кратчайший циклический путь из А 1, проходящий через три других города.

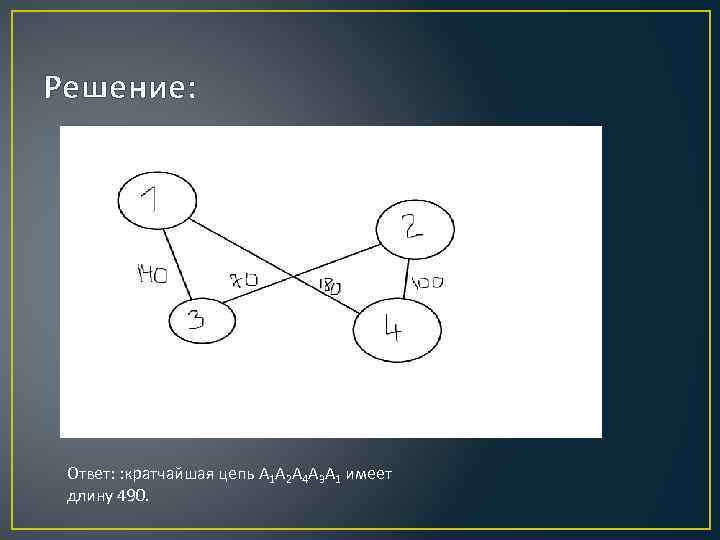
Решение: Ответ: : кратчайшая цепь А 1 А 2 А 4 А 3 А 1 имеет длину 490.

2. Вокруг дома садовник посадил 20 кустов роз, которые пронумеровал так, чтобы он мог, выйдя из дома, который находился в центре участка, обойти все розы, побывав у каждой в точности один раз. Однажды он, изменив своим правилам, полил сначала розы под номерами 19, 18, 17 и 16. В какой последовательности садовник мог бы дальше поливать розы? Ответ: 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1.

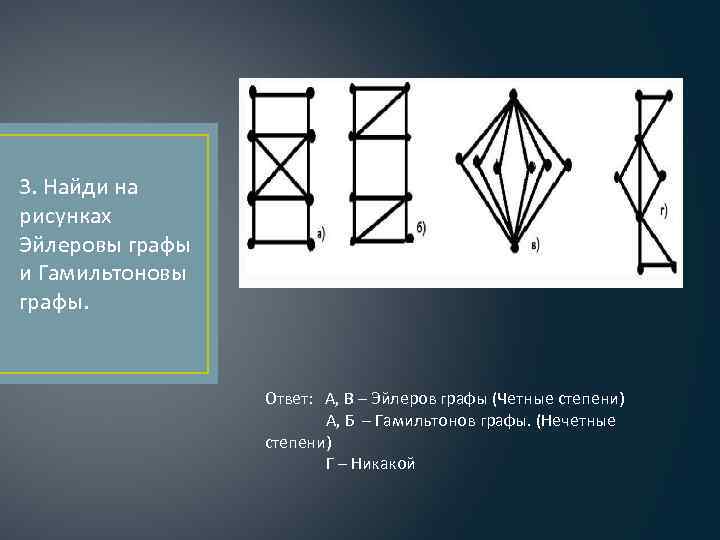
3. Найди на рисунках Эйлеровы графы и Гамильтоновы графы. Ответ: А, В – Эйлеров графы (Четные степени) А, Б – Гамильтонов графы. (Нечетные степени) Г – Никакой

Заключение • В данной курсовой работе мы познакомились с основными определениями, понятиями и результатами, связанными с гамильтоновыми графами и циклами. Так же мы рассмотрели ту часть теории сложности, которая затрагивает задачи отыскания гамильтонова цикла. И в итоги проведённых изучений была написана программа отыскания гамильтонова цикла в графе.

Список литературы • Кристофидес Н. Теория графов. Алгоритмический подход. -М. : Мир, 1978. -432 с. • Белов В. В. Теория графов: Учеб. пособие для студ. высш. техн. учеб. заведений. -М. : Высш. школа, 1976. -392 с. • Культин Н. Б. Программирование в Turbo Pascal 7. 0 и Delphi. - Санкт-Петербург: BHV, 1998. -240 c. • Уилсон Р. Дж. Введение в теорию графов. – М. : 1977. • Березина Л. Ю. Графы и их применение. – М. : Просвещение, 1979. • Оре О. Теория графо. – М. : Наука, 1968.