Курс высшей математики Часть 1 УГТУ-УПИ Лекция

Курс высшей математики Часть 1 УГТУ-УПИ

Лекция 11 1. Ранг матрицы. Базисный минор 2. Элементарные преобразования матрицы 3. Размерность и базис линейного пространства 4. Примеры базисов конкретных линейных пространств 5. Переход от одного базиса к другому 6. Связь координат элемента линейного пространства в старом и новом базисе 2

1. Ранг матрицы. Базисный минор Пусть А – матрица размера Зафиксируем k строк и k столбцов. Определение. Элементы, стоящие на их пересечении образуют квадратную матрицу порядка k. Определитель такой матрицы называется минором k-го порядка матрицы A и обозначается символом Mk. 3

Пример. 4

Определение. Ранг матрицы – наивысший порядок миноров, отличных от нуля. Обозначение В предыдущем примере все 5

Определение. Минор порядка , отличный от нуля, называется базисным минором. В примере: – базисный минор. 6

Определение. Строки и столбцы базисного минора называются базисными. В примере: – базисные строки. 7

Т 1 (о базисном миноре). Базисные строки линейно независимы. Доказательство. - базисный минор. 8

Рассмотрим базисные строки Нужно доказать их ЛНЗ. Предположим противное - ЛЗ. Тогда где 9

противоречие Базисные строки линейно независимы 10

Т 2 (о базисном миноре). Небазисные строки являются ЛК базисных строк. Доказательство. - базисный минор. 11

- алгебраическое дополнение элемента 12

- строка матрицы А с номером - базисные строки. Следствие 1. Ранг матрицы равен максимальному числу линейно независимых строк. 13

Следствие 2. Необходимым и достаточным условием равенства нулю определителя является линейная зависимость его строк. Ранг матрицы проще всего находить методом элементарных преобразований. 2. Элементарные преобразования матрицы. 1) Умножение строки на любое вещественное число, неравное нулю. 2) Сложение двух строк. 3) Перестановка местами двух строк. 4) Те же преобразования над столбцами. 14

Т Элементарные преобразования матрицы не меняют ее ранга. квазитреугольный вид все Ранг такой матрицы равен … 15

Пример. 16

3. Размерность и базис линейного пространства Определение. Размерностью линейного пространства называется максимальное число линейно независимых элементов, содержащихся в нем. а) конечномерные: 17

Размерность б) бесконечномерные: непрерывна на 18

Определение. Базисом n - мерного линейного пространства называется упорядоченная совокупность n линейно независимых элементов этого пространства. Т Любой элемент линейного пространства может быть разложен по базису единственным способом. 19

Доказательство. 1) Возможность разложения. Рассмотрим 20

2) Единственность (от противного). 21

Определение. Коэффициенты разложения элемента по базису называются координатами элемента в данном базисе. 4. Примеры базисов конкретных линейных пространств Пример 1. 22

Пример 2. 23

5. Переход от одного базиса к другому - старый базис - новый базис 24

- матрица перехода от 25

6. Связь координат элемента линейного пространства в старом и новом базисе. Замечание 1. Элементы, заданные в одном и том же базисе, можно сравнивать 26

Замечание 2. Элементы, заданные в одном и том же базисе, можно складывать Замечание 3. Если элементы заданы в разных базисах, для выполнения операций над ними требуется переход к другому базису. 27

Пусть - новый базис 28

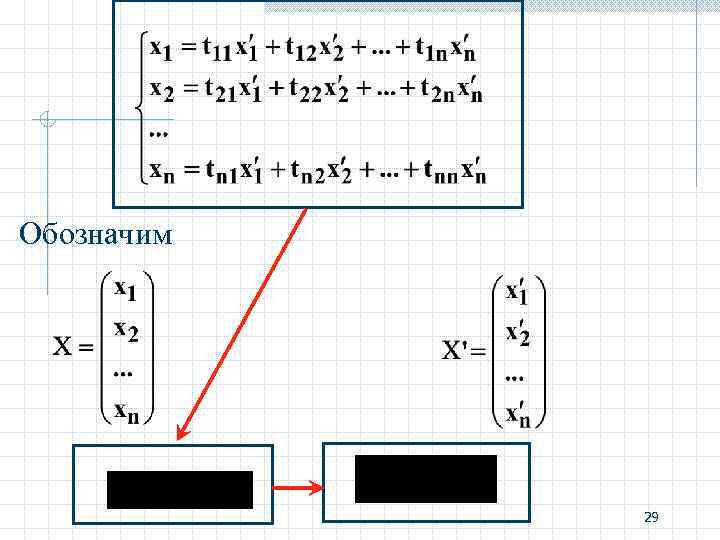Обозначим 29

МКТ 11 1. Если ранг матрицы равен 4, количество строк этой матрицы … 2. Если ранг матрицы равен 4, порядок базисного минора … 3. Если определитель матрицы пятого порядка равен нулю, ранг этой матрицы … 4. Если ранг матрицы третьего порядка равен трем, соответствующие геометрические векторы … 5. Почему возможен переход 30