Курс «Моделирование» 2

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания В этой лекции мы познакомимся с классической моделью систем массового обслуживания (СМО). Модель СМО применяется во многих областях, в том числе — для анализа качества обслуживания запросов в компьютерных системах и сетях. Одновременно она наглядно иллюстрирует суть аналитического метода моделирования. Мы познакомимся с тем, как базовые допущения позволяют использовать достаточно простой математический аппарат, а также с возможностью построения семейства моделей, охватывающих все важнейшие особенности функционирования систем и сетей массового обслуживания. Пример практического применения аналитического моделирования СМО рассмотрен в лабораторной работе № 2.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 1 Базовая модель СМО 2. 1. 1 Задачи анализа процессов массового обслуживания Примеры процессов массового обслуживания: - покупатели у касс супермаркета; - грузовые поезда на подходах к станции; - запросы на обработку данных сервером. Общие свойства процессов МО: - случайные интервалы запросов на обслуживание; - случайная длительность обслуживания; - наличие очередей к обслуживающему ресурсу. Особенности процессов МО: - условия обслуживания запросов разных типов; - приоритеты запросов; - дисциплины ожидания и обслуживания. Показатели качества обслуживания: - среднее время ожидания; - среднее количество запросов в очереди; - загрузка обслуживающего ресурса.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 1 Базовая модель массового обслуживания 2. 1. 2 Концептуальная базовая модель СМО Основные допущения модели: - независимо от физической природы выделяются объекты «запросы» Z, которые поступают от условного источника с постоянной средней интенсивностью λ. При этом интервалы между запросами случайны; - обслуживание запросов выполняет «обслуживающий блок» (ОП), который полностью занимается одним запросом на время обслуживания V. Время обслуживания содержит случайную составляющую; - если в момент появления запроса ОП занято, запрос может ожидать его освобождения в очереди (О) в течение времени W. Длина очереди не ограничена; - полное время пребывания запроса в СМО составляет U = W+V. Значения W и U случайны и требуется определить их средние значения.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 1 Базовая модель СМО 2. 1. 2 Концептуальная модель Дополнительно допускаем: Интервалы τ в простейшем потоке с интенсивностью λ подчиняются Входной поток запросов характеризуется: экспоненциальному - стационарностью - λ(t) = const = λ; закону с плотностью вероятности - ординарностью — в один момент времени поступает не более одного запроса; - отсутствием последействия — интервал между При этом длительность 2/3 всех интервалов запросами не зависит от предыстории. меньше среднего значения Это простейший поток, который полностью определяется значением интенсивности λ. Те же допущения можно сделать для потока обслуживания — с интенсивностью μ = 1/V. Свойства простейшего потока: - полностью задается величиной интенсивности ( λ или μ); - создает наиболее сложные условия обслуживания (короткие интервалы — чаще, чем длинные); - устойчив: сумма нескольких таких потоков дает также простейший поток.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 1 Базовая модель СМО 2. 1. 3 Математический аппарат Граф состояний СМО Представим функционирование СМО с помощью графа переходов, в котором номер вершины соответствует количеству запросов в системе. Переход в «старшее» состояние выполняется с интенсивностью λ, а в Система дифф. уравнений «младшее» - с интенсивностью μ. переходов Каждое K-е состояние характеризуется вероятностью Pk. Динамика переходов описывается системой дифф. уравнений. В стационарном режиме эта система вырождается в систему алгебраических Система алгебраических уравнений. уравнений вероятностей состояний Решение системы алгебраических уравнений позволяет полностью определить значения Pk исходя из λ и μ.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 1 Базовая модель СМО 2. 1. 4 Определение вероятностей состояний Последовательность решения уравнений: 0) Исходная система уравнений 1) Выражаем вероятности Pk через P 0 2) Учитываем, что сумма вероятностей =1 3) Применяем сумму геометрич. прогрессии 4) Находим формулы для вероятностей Pk с учетом загрузки

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 1 Базовая модель СМО 2. 1. 5 Расчет показателей качества обслуживания Порядок расчета: 1) Исходя из вероятностей определяем среднее число запросов в системе m и среднюю длину очереди l 2) По форуле Литла определяем среднее Время пребывания запроса в системе U а затем - среднее время ожидания W Зависимость показателей качества от загрузки системы Оптимальной считается загруженность СМО на 40 -60% При большей загрузке быстро растет время ожидания (например, при загрузке 90% запросы 90% времени проводят в очереди). При меньшей загрузке — ресурсы СМО недоиспользуются

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 2 Спектр моделей СМО 2. 2. 1 Обобщение концептуальной модели СМО Применяются следующие расширения базовой модели СМО: - в систему могут поступать несколько потоков запросов с интенсивностями λk - потоки запросов могут характеризоваться разными параметрами времени обслуживания; - возможно обслуживание запросов в многоканальном режиме (любой свободный); - запросы могут иметь относительные приоритеты (обгон в очереди) или абсолютные приоритеты (прерывание обслуживания); - из-за ограничений очередей по длине, могут возникать отказы в обслуживании и выталкивания низкоприоритетных запросов; - из-за ограничений на время выполнения Для всех перечисленных расширений получены могут возникать уходы и потери формулы для расчета показателей обслуживания. низкоприоритетных запросов. Они описаны в специальной литературе.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 2 Спектр моделей СМО 2. 2. 2 Классификация и обозначения моделей СМО Признаки классификации: - количество каналов; - характер потоков; Примеры популярных моделей: - ограничения очереди. - М/M/1 - базовая одноканальная модель СМО Позиция: (простейшие потоки входа и обслуживания); 1 — входной поток; - М/M/n - модель СМО с n каналами и 2 — поток обслуживания; простейшими потоками; 3 — количество каналов обслуживания; - М/G/1 — одноканальная модель с произвольным 4 — число мест в очереди. распределением времени обслуживания; - М/M/n/L — многоканальная модель с Характер потоков: ограниченной очередью. - М — простейший поток; - G — произвольное распределение; - D — детерминированный поток

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 2 Спектр моделей СМО 2. 2. 3 Расчет многоканальной СМО Особенности многоканальной СМО: 1) В графе переходов интенсивность обслуживания пропорциональна числу задействованных каналов. 2) Вывод формул выполняется по схеме для базовой СМО с учетом количества каналов n 3) По результатам расчетов многоканальное обслуживание ( «с общей очередью» ) эффективнее одноканального ( «с раздельными очередями» ), особенно при значительной загрузке системы.

Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 2 Спектр моделей СМО 2. 2. 4 СМО с произвольным временем обслуживания Расчет СМО M/G/1 ведется с Формулы Паллачека-Хинчина для СМО M/G/1 использованием формул, выведенных математиками Паллачеком и Хинчиным. Формулы для СМО M/М/1 получаются из них как частный случай для коэффициента Исходная формула l для СМО M/М/1 вариации времени обслуживания = 1. Формулы подтверждают, что простейший поток обслуживания дает максимальную оценку ожидания запросов в очереди.

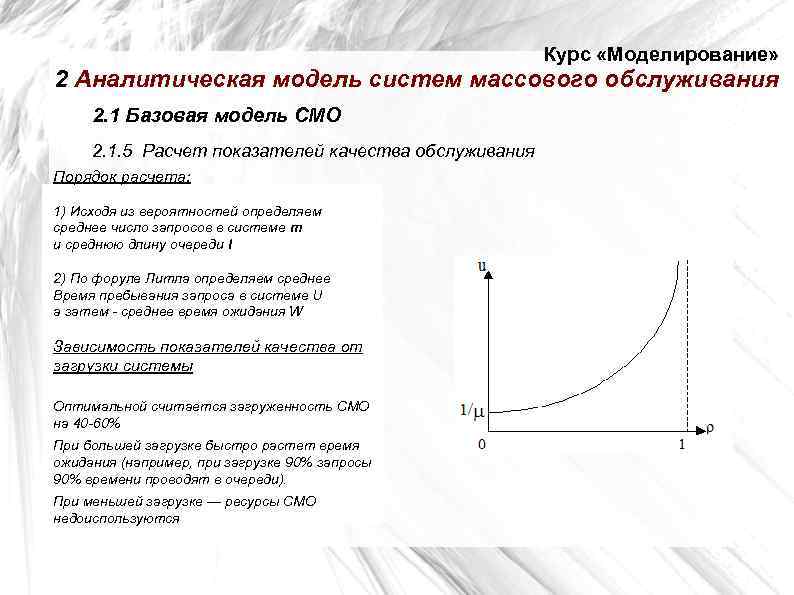
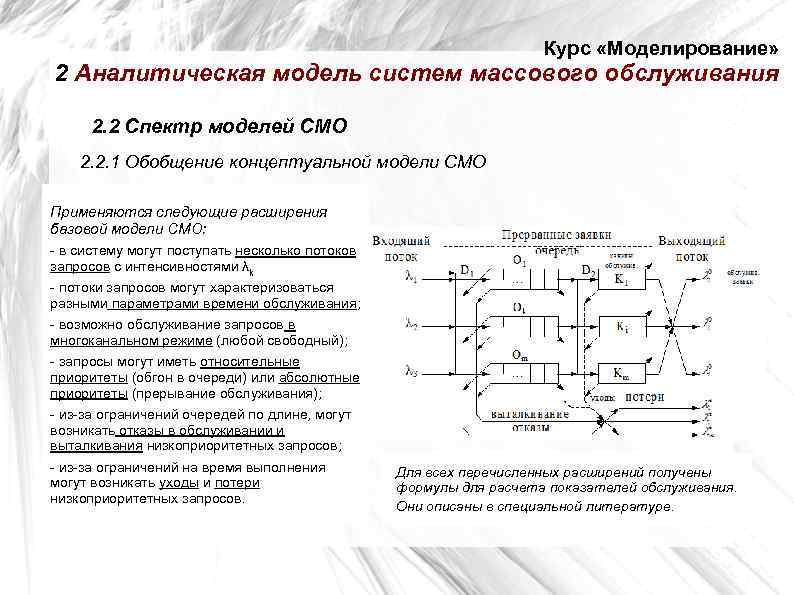
Курс «Моделирование» 2 Аналитическая модель систем массового обслуживания 2. 3 Понятие о расчете сетей МО Сеть МО — это совокупность взаимосвязанных СМО, обслуживающих общий поток запросов. Время пребывания запроса в сети определяется как суммарное время пребывания во всех СМО. На рисунке приведен пример сети МО, моделирующей обслуживание потока запросов к серверу с учетом нескольких обращений к дисковой подсистеме из m однотипных устройств. Расчет полного времени U пребывания запроса в сети МО основан на Исходные данные расчета: использовании базовой модели СМО и - интенсивность входных запросов λ 0 определении количества обращений к - время обработки обращения ЦП ν 1 дискам и к процессору. - время обработки обращения МД ν 2 - среднее число обращений к дискам n