Курс лекций по теории

































































Лекции_по динамике и устойчивости.ppt
- Количество слайдов: 89
 Курс лекций по теории колебаний Д-р техн. наук, проф. Ю. Л. Рутман
Курс лекций по теории колебаний Д-р техн. наук, проф. Ю. Л. Рутман
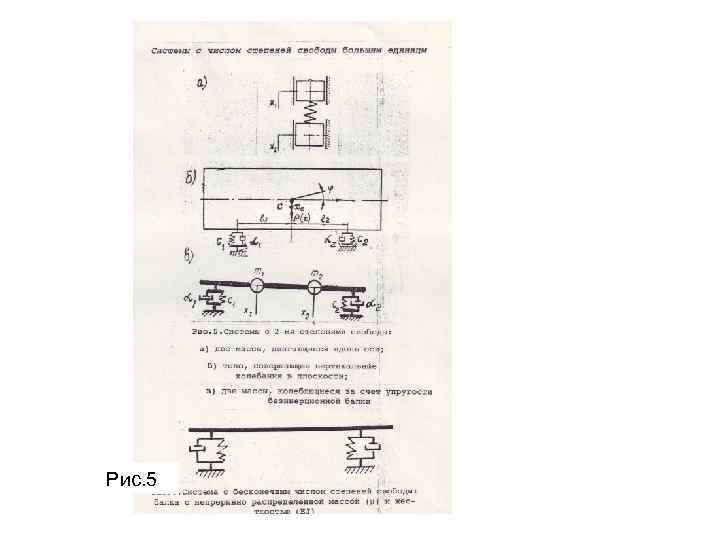
 Рис. 5
Рис. 5
 Свободные колебания линейной системы Рассмотрим решение задач о свободных колебаниях линейной системы с одной степенью свободы (линейного осциллятора). Уравнение колебаний линейного осциллятора имеет вид: Введем обозначения:
Свободные колебания линейной системы Рассмотрим решение задач о свободных колебаниях линейной системы с одной степенью свободы (линейного осциллятора). Уравнение колебаний линейного осциллятора имеет вид: Введем обозначения:
 Свободные колебания линейной системы Теперь вместо (1) можно записать По правилу решения линейных дифференциальных уравнений с постоянными коэффициентами составляем характеристическое уравнение
Свободные колебания линейной системы Теперь вместо (1) можно записать По правилу решения линейных дифференциальных уравнений с постоянными коэффициентами составляем характеристическое уравнение
 Свободные колебания линейной системы Обозначим При p 2 > n 2 решение уравнения (3) будет определяться формулой или где
Свободные колебания линейной системы Обозначим При p 2 > n 2 решение уравнения (3) будет определяться формулой или где
 Свободные колебания линейной системы при наличии вязких сил свободные колебания Следовательно, массы представляют собой затухающих процесс – рис. 6. Процесс, показанный на рис. 6 , называют периодическими затухающими колебаниями, несмотря на неточность такого названия. Под периодом этих колебаний понимают время между двумя максимальными смещениями Величину p 1 называют круговой частотой колебаний. Размерность p 1 – 1/с. Часто вместо круговой частоты используют техническую частоту, которая измеряется в герцах:
Свободные колебания линейной системы при наличии вязких сил свободные колебания Следовательно, массы представляют собой затухающих процесс – рис. 6. Процесс, показанный на рис. 6 , называют периодическими затухающими колебаниями, несмотря на неточность такого названия. Под периодом этих колебаний понимают время между двумя максимальными смещениями Величину p 1 называют круговой частотой колебаний. Размерность p 1 – 1/с. Часто вместо круговой частоты используют техническую частоту, которая измеряется в герцах:
 Свободные колебания линейной системы Частота в герцах равна числу колебаний в секунду. При отсутствии вязких сил, то есть когда n=0 (осциллятор линейно- упругий), формулы (8), (11) упрощаются: Иногда частоту p линейно-упругого осциллятора связывают со статической деформацией f ст упругого элемента силой, равной весу тела
Свободные колебания линейной системы Частота в герцах равна числу колебаний в секунду. При отсутствии вязких сил, то есть когда n=0 (осциллятор линейно- упругий), формулы (8), (11) упрощаются: Иногда частоту p линейно-упругого осциллятора связывают со статической деформацией f ст упругого элемента силой, равной весу тела
 Свободные колебания линейной системы имеют место формулы: Легко видеть, что Найдем постоянные интегрирования c 1 и c 2 в уравнении (7). Продифференцируем (7):
Свободные колебания линейной системы имеют место формулы: Легко видеть, что Найдем постоянные интегрирования c 1 и c 2 в уравнении (7). Продифференцируем (7):
 Свободные колебания линейной системы и (15), а также используя (1′), получаем Пологая t=0 в (7) Из (16) следует или Для линейно-упругого осциллятора n=0, вместо (18) получаем
Свободные колебания линейной системы и (15), а также используя (1′), получаем Пологая t=0 в (7) Из (16) следует или Для линейно-упругого осциллятора n=0, вместо (18) получаем
 Свободные колебания линейной системы или где Отметим, что аргумент «pt+φ» в (8) и (19′) называется фазой, а величина φ – начальной фазой. Отношение двух последовательных максимальных отклонений осциллятора при свободных колебаниях в соответствии с формулой (8) равно
Свободные колебания линейной системы или где Отметим, что аргумент «pt+φ» в (8) и (19′) называется фазой, а величина φ – начальной фазой. Отношение двух последовательных максимальных отклонений осциллятора при свободных колебаниях в соответствии с формулой (8) равно
 Свободные колебания линейной системы где Ak, Ak+1 – см. рис. 6. Таким образом, последовательные максимальные отклонения осциллятора от равновесного положения представляют собой члены геометрической прогрессии со знаменателем e= -n τ. При 1 n=0 знаменатель прогрессии e 0=1, то есть все амплитуды равны, и колебания происходят по синусоидальному закону. Чаще рассматривают не отношение двух последовательных отклонений, а логарифм этого отношения, который называют логарифмическим декрементом колебания:
Свободные колебания линейной системы где Ak, Ak+1 – см. рис. 6. Таким образом, последовательные максимальные отклонения осциллятора от равновесного положения представляют собой члены геометрической прогрессии со знаменателем e= -n τ. При 1 n=0 знаменатель прогрессии e 0=1, то есть все амплитуды равны, и колебания происходят по синусоидальному закону. Чаще рассматривают не отношение двух последовательных отклонений, а логарифм этого отношения, который называют логарифмическим декрементом колебания:
 Свободные колебания линейной системы Для модели (1) существует критическое значение параметра α , превышение которого приводит к исчезновению колебательных процессов в модели и к появлению затухающих апериодических процессов. Это критическое значение находится из равенства: Действительно, решение уравнения (3) имеет вид (7) лишь при p>n. При p
Свободные колебания линейной системы Для модели (1) существует критическое значение параметра α , превышение которого приводит к исчезновению колебательных процессов в модели и к появлению затухающих апериодических процессов. Это критическое значение находится из равенства: Действительно, решение уравнения (3) имеет вид (7) лишь при p>n. При p
 Свободные колебания линейной системы Движение, описываемое выражением (25), неколебательное (рис. ). В случае, когда p=n, решение уравнение (3) имеет вид Это решение по характеру не отличается от показанного на рис. . Считая n в (24) критическим значением затухания, получаем Модель (1) позволяет определить усилия, возникающие при ударе тела о препятствие. Действительно, будем полагать, что m – масса ударяющегося о препятствие тела, c – суммарная контактная жесткость тела и препятствия. Тогда процесс соударения (до отскока тела) описывается линейной моделью (1) при начальных условиях:
Свободные колебания линейной системы Движение, описываемое выражением (25), неколебательное (рис. ). В случае, когда p=n, решение уравнение (3) имеет вид Это решение по характеру не отличается от показанного на рис. . Считая n в (24) критическим значением затухания, получаем Модель (1) позволяет определить усилия, возникающие при ударе тела о препятствие. Действительно, будем полагать, что m – масса ударяющегося о препятствие тела, c – суммарная контактная жесткость тела и препятствия. Тогда процесс соударения (до отскока тела) описывается линейной моделью (1) при начальных условиях:
 Свободные колебания линейной системы Рис. 7 Апериодическое движение осциллятора
Свободные колебания линейной системы Рис. 7 Апериодическое движение осциллятора
 Свободные колебания линейной системы где v – скорость наталкивающегося на препятствие тела. При начальных условиях (29) решение (18) имеет вид Определим максимум усилия соударения Q:
Свободные колебания линейной системы где v – скорость наталкивающегося на препятствие тела. При начальных условиях (29) решение (18) имеет вид Определим максимум усилия соударения Q:
 Свободные колебания линейной системы Так как потери механической энергии при ударе невелики e -πε/2 ≈1, то можно считать, что соответствует максимальной силе удара в консервативной системе (α=0).
Свободные колебания линейной системы Так как потери механической энергии при ударе невелики e -πε/2 ≈1, то можно считать, что соответствует максимальной силе удара в консервативной системе (α=0).
 • Вынужденные колебания линейной системы Рассмотрим решение задач о вынужденных колебаниях линейного осциллятора. Уравнение вынужденных колебаний линейного осциллятора имеет вид ( ). После деления на m с учетом (2) получаем: Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме какого-либо его частного решения x * (t) и общего решения однородного уравнения. Таким образом, решение (33) имеет вид
• Вынужденные колебания линейной системы Рассмотрим решение задач о вынужденных колебаниях линейного осциллятора. Уравнение вынужденных колебаний линейного осциллятора имеет вид ( ). После деления на m с учетом (2) получаем: Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме какого-либо его частного решения x * (t) и общего решения однородного уравнения. Таким образом, решение (33) имеет вид
 • Вынужденные колебания линейной системы Частное решение неоднородного линейного дифференциального уравнения можно записать в виде где - правая часть дифференциального уравнения; - реакция динамической системы, описываемой данным уравнением, на единичный импульс ( G(t) называется функцией Грина). Таким образом, для уравнения (33) G(t) находится по формуле (18) при начальных условиях
• Вынужденные колебания линейной системы Частное решение неоднородного линейного дифференциального уравнения можно записать в виде где - правая часть дифференциального уравнения; - реакция динамической системы, описываемой данным уравнением, на единичный импульс ( G(t) называется функцией Грина). Таким образом, для уравнения (33) G(t) находится по формуле (18) при начальных условиях
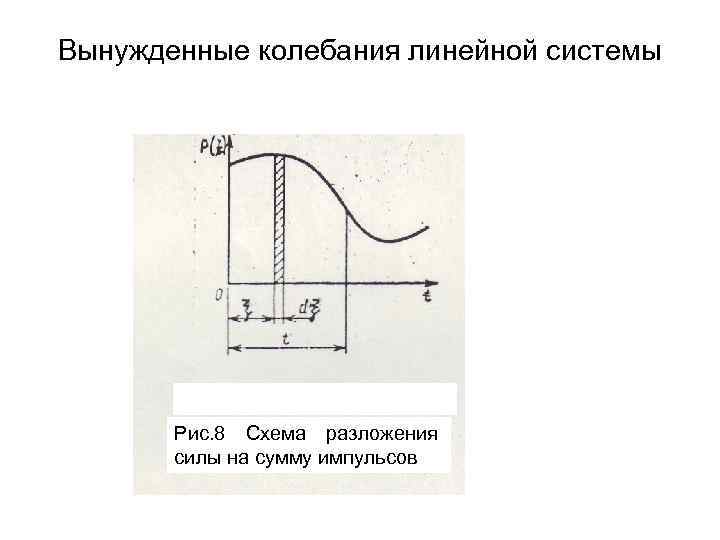
 Вынужденные колебания линейной системы Рис. 8 Схема разложения силы на сумму импульсов
Вынужденные колебания линейной системы Рис. 8 Схема разложения силы на сумму импульсов
 • Вынужденные колебания линейной системы Так как в рассматриваемом случае , то из (36) с учетом (38) получаем Интеграл (39) называется интегралом Дюамеля Так как , то постоянные c 1 и c 2 в (35) определяются по формулам (17). В результате получаем
• Вынужденные колебания линейной системы Так как в рассматриваемом случае , то из (36) с учетом (38) получаем Интеграл (39) называется интегралом Дюамеля Так как , то постоянные c 1 и c 2 в (35) определяются по формулам (17). В результате получаем
 • Вынужденные колебания линейной системы
• Вынужденные колебания линейной системы
 • Вынужденные колебания линейной системы Отметим, что формулу (36) можно интерпретировать как соотношение, выражающее принцип наложения (суперпозиции). Произвольная нагрузка P(t) разлагается на бесконечное множество бесконечно малых импульсивных нагрузок d. J=P( ξ )d ξ (рис. ). Каждая из таких нагрузок вызывает в момент t > ξ смещение где G – реакция системы на единичный импульс. Если в начальный момент система неподвижна, то полное смещение в момент t равно сумме смещений, вызываемых всеми элементарными импульсами, приложенными при t < ξ. Иначе говоря,
• Вынужденные колебания линейной системы Отметим, что формулу (36) можно интерпретировать как соотношение, выражающее принцип наложения (суперпозиции). Произвольная нагрузка P(t) разлагается на бесконечное множество бесконечно малых импульсивных нагрузок d. J=P( ξ )d ξ (рис. ). Каждая из таких нагрузок вызывает в момент t > ξ смещение где G – реакция системы на единичный импульс. Если в начальный момент система неподвижна, то полное смещение в момент t равно сумме смещений, вызываемых всеми элементарными импульсами, приложенными при t < ξ. Иначе говоря,
 • Вынужденные колебания линейной системы что совпадает с (36). Если начальные условия ненулевые, то решение состоит из двух слагаемых, то есть производится суперпозиция результатов действия нагрузки и результатов действия начальных возмущений. Формула (40) полностью решает вопрос об аналитическом описании решения задачи вынужденных колебаний линейного осциллятора. Конечно, при сравнительно простых типах P(t) аналитическое решение (33) может быть получено и другими методами. Однако общим методом отыскания таких решений является соотношение (40).
• Вынужденные колебания линейной системы что совпадает с (36). Если начальные условия ненулевые, то решение состоит из двух слагаемых, то есть производится суперпозиция результатов действия нагрузки и результатов действия начальных возмущений. Формула (40) полностью решает вопрос об аналитическом описании решения задачи вынужденных колебаний линейного осциллятора. Конечно, при сравнительно простых типах P(t) аналитическое решение (33) может быть получено и другими методами. Однако общим методом отыскания таких решений является соотношение (40).
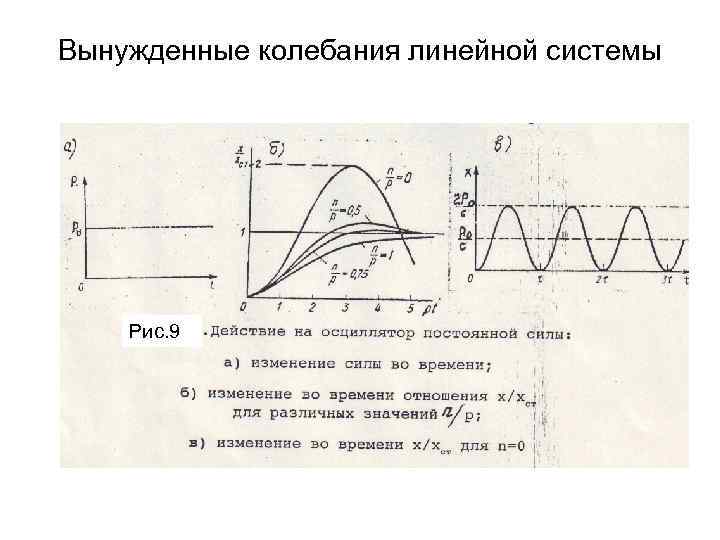
 • Вынужденные колебания линейной системы Рассмотрим применение формулы (40) на простом примере. Пусть на систему внезапно подействовала постоянная сила (рис. , ): В этом случае, применяя (40), получаем Интеграл (41) удобно вычислить, перейдя к показательной форме записи тригонометрической функции. Как известно,
• Вынужденные колебания линейной системы Рассмотрим применение формулы (40) на простом примере. Пусть на систему внезапно подействовала постоянная сила (рис. , ): В этом случае, применяя (40), получаем Интеграл (41) удобно вычислить, перейдя к показательной форме записи тригонометрической функции. Как известно,
 • Вынужденные колебания линейной системы Используя (42) при вычислении интеграла (41), имеем Учитывая, что m(n 2+p 12)=mp 2=c, а P 0/c=xст представляет собой статическую деформацию системы силой P 0, из (43) получаем
• Вынужденные колебания линейной системы Используя (42) при вычислении интеграла (41), имеем Учитывая, что m(n 2+p 12)=mp 2=c, а P 0/c=xст представляет собой статическую деформацию системы силой P 0, из (43) получаем
 Вынужденные колебания линейной системы Рис. 9
Вынужденные колебания линейной системы Рис. 9
 Вынужденные колебания линейной системы
Вынужденные колебания линейной системы
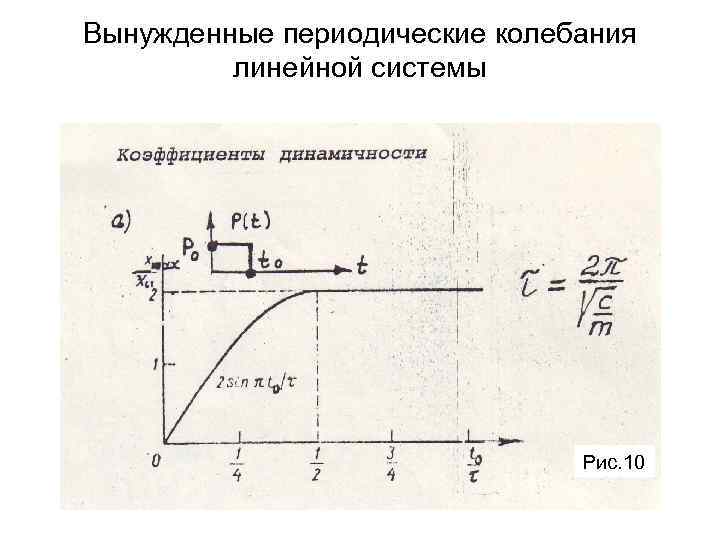
 Вынужденные периодические колебания линейной системы Рис. 10
Вынужденные периодические колебания линейной системы Рис. 10
 Вынужденные колебания линейной системы Рис. 11
Вынужденные колебания линейной системы Рис. 11
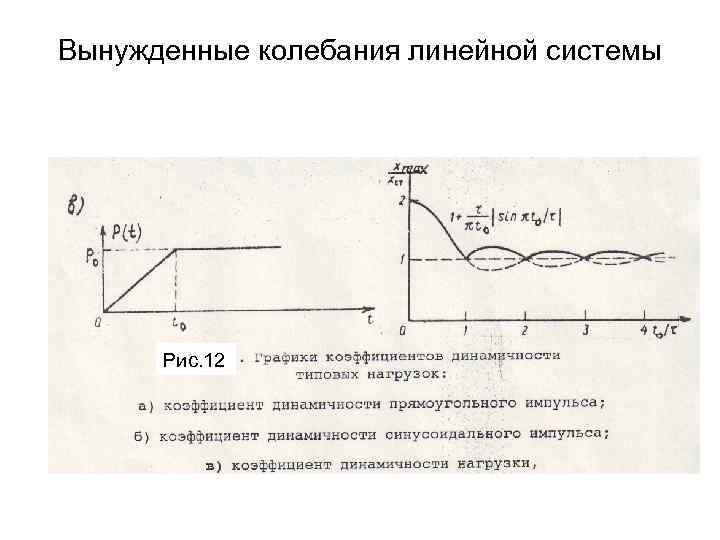
 Вынужденные колебания линейной системы Рис. 12
Вынужденные колебания линейной системы Рис. 12
 Вынужденные периодические колебания линейной системы Подставляя (49) в (48) получаем
Вынужденные периодические колебания линейной системы Подставляя (49) в (48) получаем
 Вынужденные периодические колебания линейной системы
Вынужденные периодические колебания линейной системы
 Вынужденные периодические колебания линейной системы
Вынужденные периодические колебания линейной системы
 Вынужденные периодические колебания линейной системы
Вынужденные периодические колебания линейной системы
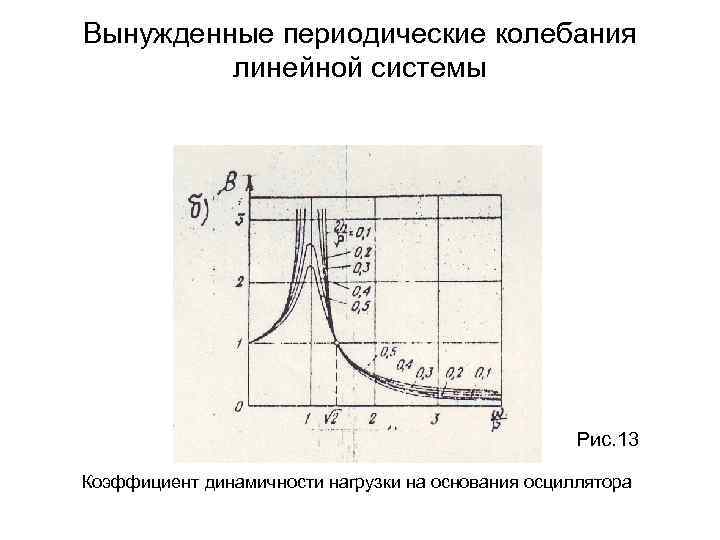
 Вынужденные периодические колебания линейной системы Рис. 13 Коэффициент динамичности нагрузки на основания осциллятора
Вынужденные периодические колебания линейной системы Рис. 13 Коэффициент динамичности нагрузки на основания осциллятора
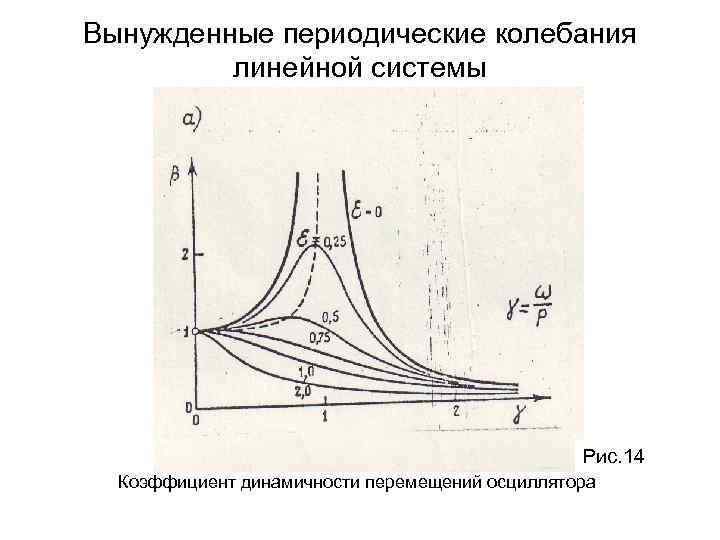
 Вынужденные периодические колебания линейной системы Рис. 14 Коэффициент динамичности перемещений осциллятора
Вынужденные периодические колебания линейной системы Рис. 14 Коэффициент динамичности перемещений осциллятора
 Вынужденные периодические колебания линейной системы
Вынужденные периодические колебания линейной системы
 Вынужденные периодические колебания линейной системы
Вынужденные периодические колебания линейной системы
 Вынужденные периодические колебания линейной системы
Вынужденные периодические колебания линейной системы
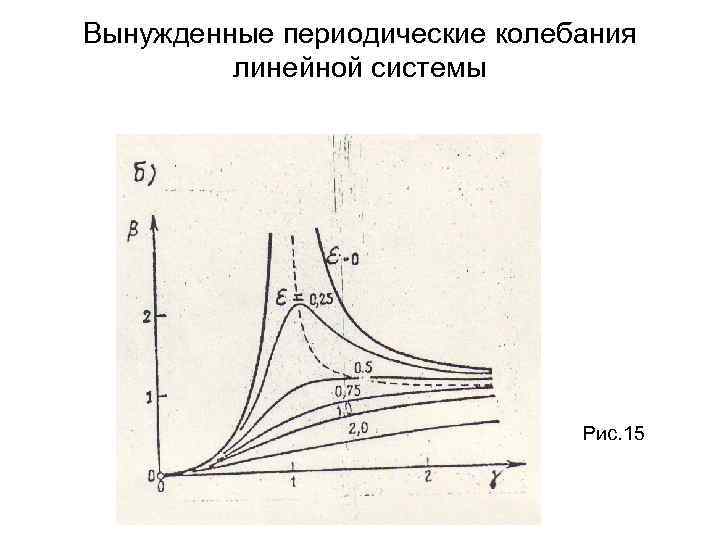
 Вынужденные периодические колебания линейной системы Рис. 15
Вынужденные периодические колебания линейной системы Рис. 15
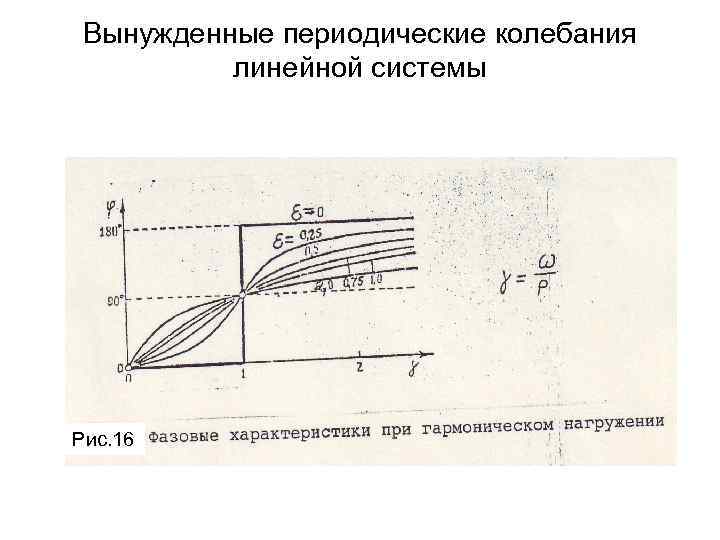
 Вынужденные периодические колебания линейной системы Рис. 16
Вынужденные периодические колебания линейной системы Рис. 16
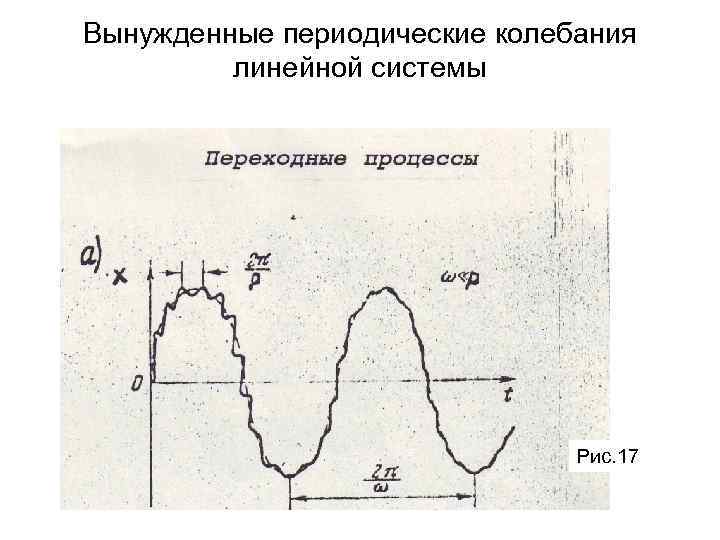
 Вынужденные периодические колебания линейной системы Рис. 17
Вынужденные периодические колебания линейной системы Рис. 17
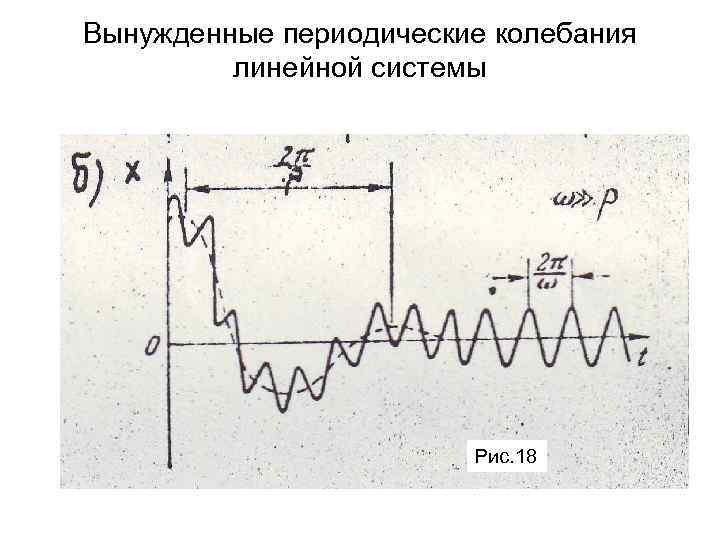
 Вынужденные периодические колебания линейной системы Рис. 18
Вынужденные периодические колебания линейной системы Рис. 18
 Вынужденные периодические колебания линейной системы Рис. 18
Вынужденные периодические колебания линейной системы Рис. 18
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
 Колебания систем с конечным числом степеней свободы U – потенциал упругих сил, Т – кинетическая энергия
Колебания систем с конечным числом степеней свободы U – потенциал упругих сил, Т – кинетическая энергия
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
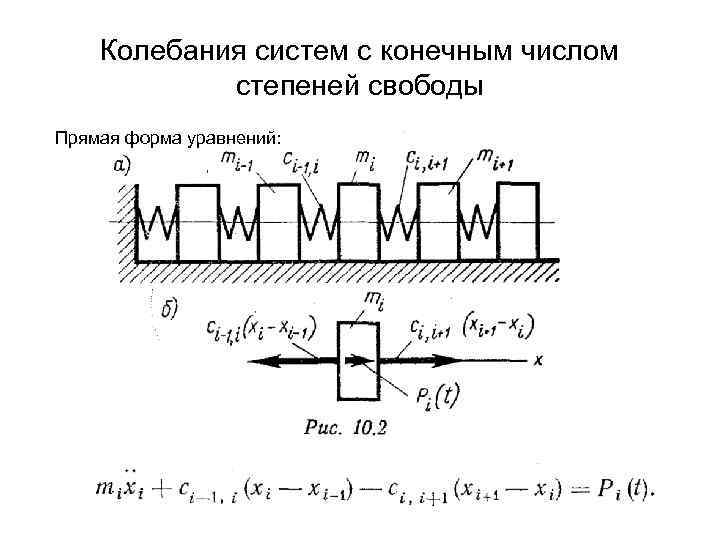
 Колебания систем с конечным числом степеней свободы Прямая форма уравнений: Уравнения (1) описывают колебания упругой системы с n степенями свободы. Если матрица масс диагональная: , то
Колебания систем с конечным числом степеней свободы Прямая форма уравнений: Уравнения (1) описывают колебания упругой системы с n степенями свободы. Если матрица масс диагональная: , то
 Колебания систем с конечным числом степеней свободы Прямая форма уравнений:
Колебания систем с конечным числом степеней свободы Прямая форма уравнений:
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
 Колебания систем с конечным числом степеней свободы
Колебания систем с конечным числом степеней свободы
 Определение частот и форм свободных колебания
Определение частот и форм свободных колебания
 Определение частот и форм свободных колебания
Определение частот и форм свободных колебания
 Определение частот и форм свободных колебания
Определение частот и форм свободных колебания
 Определение частот и форм свободных колебания
Определение частот и форм свободных колебания
 Определение частот и форм свободных колебания
Определение частот и форм свободных колебания
 Определение частот и форм свободных колебания Первая собственная форма
Определение частот и форм свободных колебания Первая собственная форма
 Сейсмика
Сейсмика
 Уравнения движения
Уравнения движения
 Вывод формул СНи. Па
Вывод формул СНи. Па
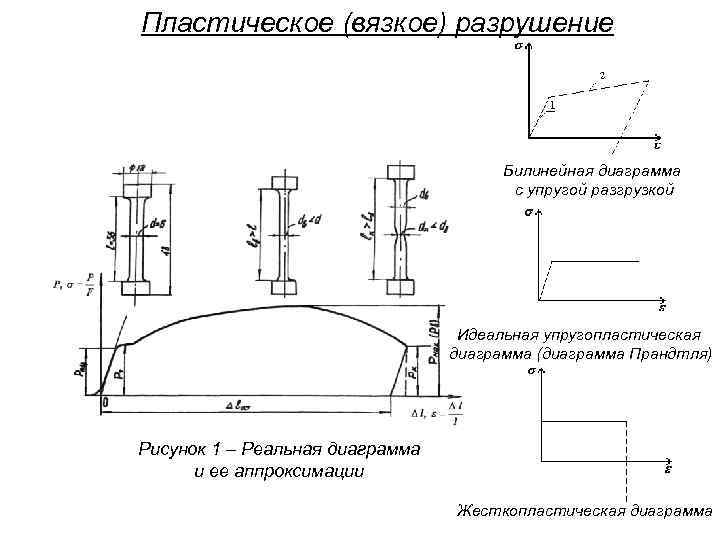
 Пластическое (вязкое) разрушение Билинейная диаграмма с упругой разгрузкой Идеальная упругопластическая диаграмма (диаграмма Прандтля) Рисунок 1 – Реальная диаграмма и ее аппроксимации Жесткопластическая диаграмма
Пластическое (вязкое) разрушение Билинейная диаграмма с упругой разгрузкой Идеальная упругопластическая диаграмма (диаграмма Прандтля) Рисунок 1 – Реальная диаграмма и ее аппроксимации Жесткопластическая диаграмма
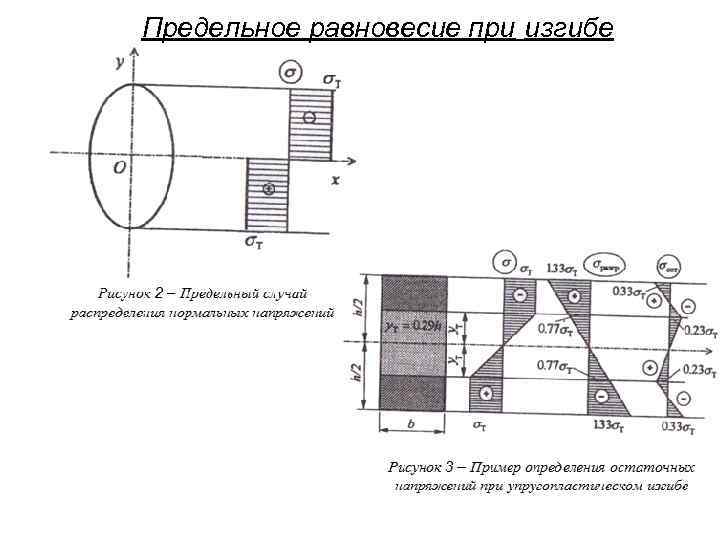
 Предельное равновесие при изгибе
Предельное равновесие при изгибе
 Предельное равновесие при изгибе
Предельное равновесие при изгибе
 Предельные моменты при изгибе для различных сечений
Предельные моменты при изгибе для различных сечений
 Методика анализа Нелинейная модель с одной степенью свободы • Нелинейная модель с одной степенью свободы начала применятся в работах Ньюмарка Н. , Розенблюэта Э. , Ивена В. , Велетсос А. и др. и применяется до сих пор в исследованиях Датта Т. К. и Чопры А. К. Рис. 1. Билинейная диаграмма с упругой разгрузкой
Методика анализа Нелинейная модель с одной степенью свободы • Нелинейная модель с одной степенью свободы начала применятся в работах Ньюмарка Н. , Розенблюэта Э. , Ивена В. , Велетсос А. и др. и применяется до сих пор в исследованиях Датта Т. К. и Чопры А. К. Рис. 1. Билинейная диаграмма с упругой разгрузкой
 Модель, представленная на рис. 1 а, описывается дифференциальным уравнением (1). Петлю гистерезиса и циклическую диаграмму деформирования на рис. 1 б характеризуют следующие параметры: где FТ – предельная нагрузка системы с одной степенью свободы. Для решения задачи о предельном равновесии жесткопластических конструкций предлагается применить метод псевдожесткостей.
Модель, представленная на рис. 1 а, описывается дифференциальным уравнением (1). Петлю гистерезиса и циклическую диаграмму деформирования на рис. 1 б характеризуют следующие параметры: где FТ – предельная нагрузка системы с одной степенью свободы. Для решения задачи о предельном равновесии жесткопластических конструкций предлагается применить метод псевдожесткостей.
 Движение системы с n степенями свободы описывается n дифференциальными уравнениями второго порядка. – вектор относительных перемещений (в системе координат, связанной с основанием); – матрицы масс и диссипации системы (n x n); – нелинейная гистерезисная функция (нелинейная зависимость сила – перемещение); – вектор, компонентами которого являются косинусы углов между направлениями перемещений по степеням свободы и вектором ускорения основания; – компонента сейсмического ускорения основания
Движение системы с n степенями свободы описывается n дифференциальными уравнениями второго порядка. – вектор относительных перемещений (в системе координат, связанной с основанием); – матрицы масс и диссипации системы (n x n); – нелинейная гистерезисная функция (нелинейная зависимость сила – перемещение); – вектор, компонентами которого являются косинусы углов между направлениями перемещений по степеням свободы и вектором ускорения основания; – компонента сейсмического ускорения основания
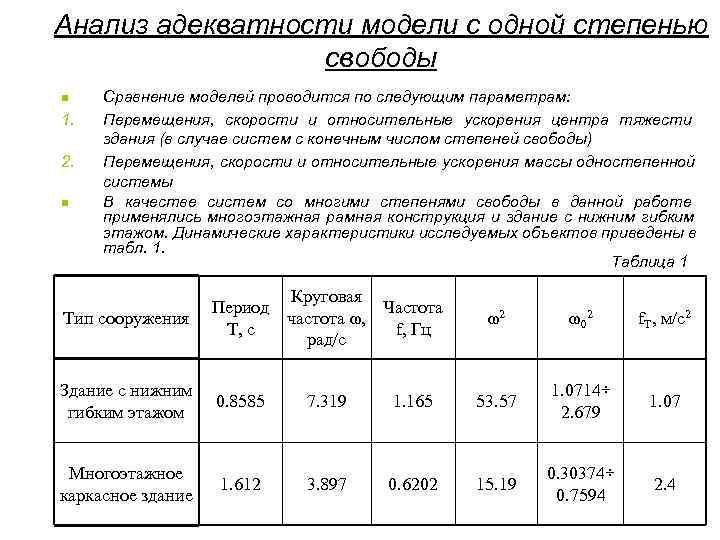
 Анализ адекватности модели с одной степенью свободы n Сравнение моделей проводится по следующим параметрам: 1. Перемещения, скорости и относительные ускорения центра тяжести здания (в случае систем с конечным числом степеней свободы) 2. Перемещения, скорости и относительные ускорения массы одностепенной системы n В качестве систем со многими степенями свободы в данной работе применялись многоэтажная рамная конструкция и здание с нижним гибким этажом. Динамические характеристики исследуемых объектов приведены в табл. 1. Таблица 1 Круговая Период Частота Тип сооружения частота ω, ω2 ω0 2 f. Т, м/с2 Т, с f, Гц рад/с Здание с нижним 1. 0714÷ 0. 8585 7. 319 1. 165 53. 57 1. 07 гибким этажом 2. 679 Многоэтажное 0. 30374÷ 1. 612 3. 897 0. 6202 15. 19 2. 4 каркасное здание 0. 7594
Анализ адекватности модели с одной степенью свободы n Сравнение моделей проводится по следующим параметрам: 1. Перемещения, скорости и относительные ускорения центра тяжести здания (в случае систем с конечным числом степеней свободы) 2. Перемещения, скорости и относительные ускорения массы одностепенной системы n В качестве систем со многими степенями свободы в данной работе применялись многоэтажная рамная конструкция и здание с нижним гибким этажом. Динамические характеристики исследуемых объектов приведены в табл. 1. Таблица 1 Круговая Период Частота Тип сооружения частота ω, ω2 ω0 2 f. Т, м/с2 Т, с f, Гц рад/с Здание с нижним 1. 0714÷ 0. 8585 7. 319 1. 165 53. 57 1. 07 гибким этажом 2. 679 Многоэтажное 0. 30374÷ 1. 612 3. 897 0. 6202 15. 19 2. 4 каркасное здание 0. 7594
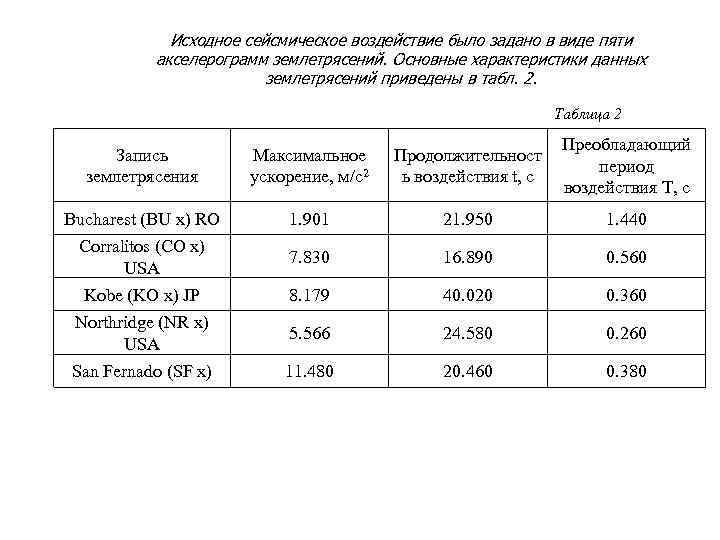
 Исходное сейсмическое воздействие было задано в виде пяти акселерограмм землетрясений. Основные характеристики данных землетрясений приведены в табл. 2. Таблица 2 Преобладающий Запись Максимальное Продолжительност период землетрясения ускорение, м/с2 ь воздействия t, с воздействия Т, с Bucharest (BU x) RO 1. 901 21. 950 1. 440 Corralitos (CO x) 7. 830 16. 890 0. 560 USA Kobe (KO x) JP 8. 179 40. 020 0. 360 Northridge (NR x) 5. 566 24. 580 0. 260 USA San Fernado (SF x) 11. 480 20. 460 0. 380
Исходное сейсмическое воздействие было задано в виде пяти акселерограмм землетрясений. Основные характеристики данных землетрясений приведены в табл. 2. Таблица 2 Преобладающий Запись Максимальное Продолжительност период землетрясения ускорение, м/с2 ь воздействия t, с воздействия Т, с Bucharest (BU x) RO 1. 901 21. 950 1. 440 Corralitos (CO x) 7. 830 16. 890 0. 560 USA Kobe (KO x) JP 8. 179 40. 020 0. 360 Northridge (NR x) 5. 566 24. 580 0. 260 USA San Fernado (SF x) 11. 480 20. 460 0. 380
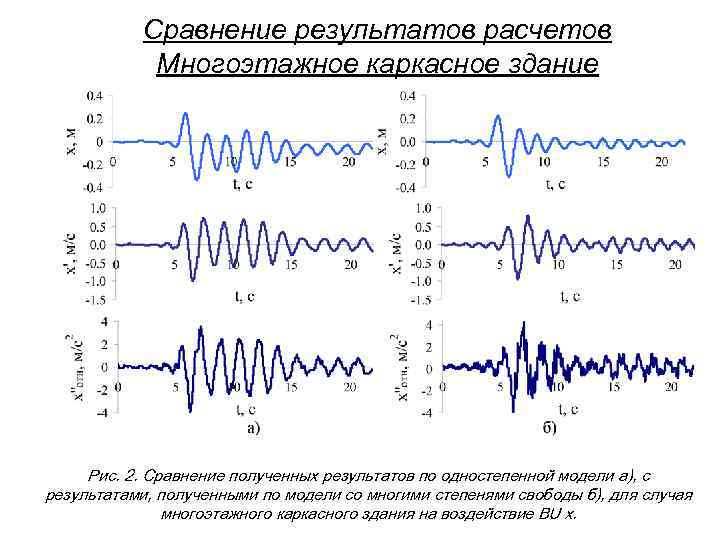
 Сравнение результатов расчетов Многоэтажное каркасное здание Рис. 2. Сравнение полученных результатов по одностепенной модели а), с результатами, полученными по модели со многими степенями свободы б), для случая многоэтажного каркасного здания на воздействие BU x.
Сравнение результатов расчетов Многоэтажное каркасное здание Рис. 2. Сравнение полученных результатов по одностепенной модели а), с результатами, полученными по модели со многими степенями свободы б), для случая многоэтажного каркасного здания на воздействие BU x.
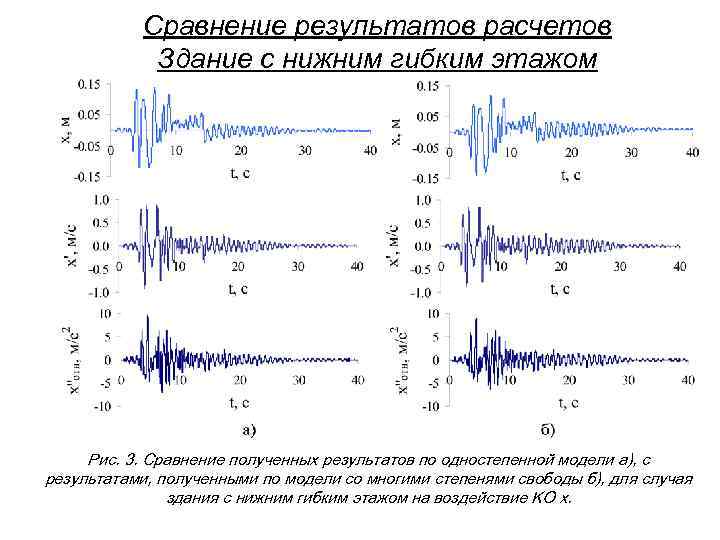
 Сравнение результатов расчетов Здание с нижним гибким этажом Рис. 3. Сравнение полученных результатов по одностепенной модели а), с результатами, полученными по модели со многими степенями свободы б), для случая здания с нижним гибким этажом на воздействие KO x.
Сравнение результатов расчетов Здание с нижним гибким этажом Рис. 3. Сравнение полученных результатов по одностепенной модели а), с результатами, полученными по модели со многими степенями свободы б), для случая здания с нижним гибким этажом на воздействие KO x.
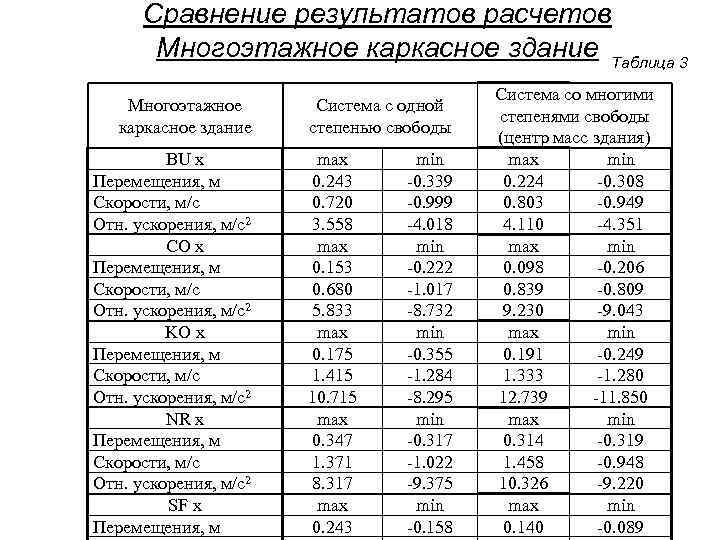
 Сравнение результатов расчетов Многоэтажное каркасное здание Таблица 3 Система со многими Многоэтажное Система с одной степенями свободы каркасное здание степенью свободы (центр масс здания) BU x max min max min Перемещения, м 0. 243 -0. 339 0. 224 -0. 308 Скорости, м/с 0. 720 -0. 999 0. 803 -0. 949 Отн. ускорения, м/с2 3. 558 -4. 018 4. 110 -4. 351 CO x max min max min Перемещения, м 0. 153 -0. 222 0. 098 -0. 206 Скорости, м/с 0. 680 -1. 017 0. 839 -0. 809 Отн. ускорения, м/с2 5. 833 -8. 732 9. 230 -9. 043 KO x max min max min Перемещения, м 0. 175 -0. 355 0. 191 -0. 249 Скорости, м/с 1. 415 -1. 284 1. 333 -1. 280 Отн. ускорения, м/с2 10. 715 -8. 295 12. 739 -11. 850 NR x max min max min Перемещения, м 0. 347 -0. 317 0. 314 -0. 319 Скорости, м/с 1. 371 -1. 022 1. 458 -0. 948 Отн. ускорения, м/с2 8. 317 -9. 375 10. 326 -9. 220 SF x max min max min Перемещения, м 0. 243 -0. 158 0. 140 -0. 089
Сравнение результатов расчетов Многоэтажное каркасное здание Таблица 3 Система со многими Многоэтажное Система с одной степенями свободы каркасное здание степенью свободы (центр масс здания) BU x max min max min Перемещения, м 0. 243 -0. 339 0. 224 -0. 308 Скорости, м/с 0. 720 -0. 999 0. 803 -0. 949 Отн. ускорения, м/с2 3. 558 -4. 018 4. 110 -4. 351 CO x max min max min Перемещения, м 0. 153 -0. 222 0. 098 -0. 206 Скорости, м/с 0. 680 -1. 017 0. 839 -0. 809 Отн. ускорения, м/с2 5. 833 -8. 732 9. 230 -9. 043 KO x max min max min Перемещения, м 0. 175 -0. 355 0. 191 -0. 249 Скорости, м/с 1. 415 -1. 284 1. 333 -1. 280 Отн. ускорения, м/с2 10. 715 -8. 295 12. 739 -11. 850 NR x max min max min Перемещения, м 0. 347 -0. 317 0. 314 -0. 319 Скорости, м/с 1. 371 -1. 022 1. 458 -0. 948 Отн. ускорения, м/с2 8. 317 -9. 375 10. 326 -9. 220 SF x max min max min Перемещения, м 0. 243 -0. 158 0. 140 -0. 089
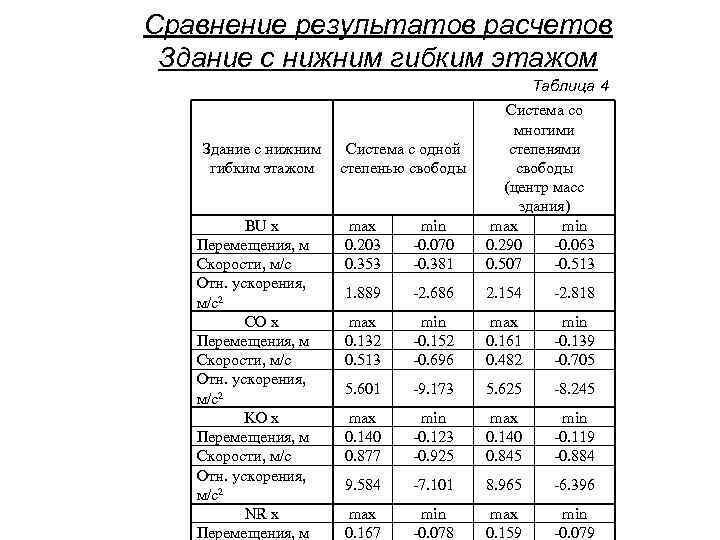
 Сравнение результатов расчетов Здание с нижним гибким этажом Таблица 4 Система со многими Здание с нижним Система с одной степенями гибким этажом степенью свободы (центр масс здания) BU x max min max min Перемещения, м 0. 203 -0. 070 0. 290 -0. 063 Скорости, м/с 0. 353 -0. 381 0. 507 -0. 513 Отн. ускорения, 1. 889 -2. 686 2. 154 -2. 818 м/с2 CO x max min max min Перемещения, м 0. 132 -0. 152 0. 161 -0. 139 Скорости, м/с 0. 513 -0. 696 0. 482 -0. 705 Отн. ускорения, 5. 601 -9. 173 5. 625 -8. 245 м/с2 KO x max min max min Перемещения, м 0. 140 -0. 123 0. 140 -0. 119 Скорости, м/с 0. 877 -0. 925 0. 845 -0. 884 Отн. ускорения, 9. 584 -7. 101 8. 965 -6. 396 м/с2 NR x max min max min Перемещения, м 0. 167 -0. 078 0. 159 -0. 079
Сравнение результатов расчетов Здание с нижним гибким этажом Таблица 4 Система со многими Здание с нижним Система с одной степенями гибким этажом степенью свободы (центр масс здания) BU x max min max min Перемещения, м 0. 203 -0. 070 0. 290 -0. 063 Скорости, м/с 0. 353 -0. 381 0. 507 -0. 513 Отн. ускорения, 1. 889 -2. 686 2. 154 -2. 818 м/с2 CO x max min max min Перемещения, м 0. 132 -0. 152 0. 161 -0. 139 Скорости, м/с 0. 513 -0. 696 0. 482 -0. 705 Отн. ускорения, 5. 601 -9. 173 5. 625 -8. 245 м/с2 KO x max min max min Перемещения, м 0. 140 -0. 123 0. 140 -0. 119 Скорости, м/с 0. 877 -0. 925 0. 845 -0. 884 Отн. ускорения, 9. 584 -7. 101 8. 965 -6. 396 м/с2 NR x max min max min Перемещения, м 0. 167 -0. 078 0. 159 -0. 079
 Расчет на малоцикловую усталость n Доля квазистатического повреждения • Доля усталостного повреждения N – число циклов нагружения e –односторонне накопленная в N f – число циклов до разрушения процессе статического и циклического (появления трещины) нагружения деформация N fi – число циклов, определяемое e f – односторонне накопленная при заданной в цикле нагружения деформация к моменту разрушения деформации (появления трещины) ε f – располагаемая пластичность (деформационная способность) материала Зависимость долговечности от величины пластической деформации в цикле нагружения определяется формулой Мэнсона-Коффина: где m – показатель пластичности, p принимаемый в пределах 0, 4… 0, 6. Предельное состояние по условиям малоциклового разрушения наступает при:
Расчет на малоцикловую усталость n Доля квазистатического повреждения • Доля усталостного повреждения N – число циклов нагружения e –односторонне накопленная в N f – число циклов до разрушения процессе статического и циклического (появления трещины) нагружения деформация N fi – число циклов, определяемое e f – односторонне накопленная при заданной в цикле нагружения деформация к моменту разрушения деформации (появления трещины) ε f – располагаемая пластичность (деформационная способность) материала Зависимость долговечности от величины пластической деформации в цикле нагружения определяется формулой Мэнсона-Коффина: где m – показатель пластичности, p принимаемый в пределах 0, 4… 0, 6. Предельное состояние по условиям малоциклового разрушения наступает при:
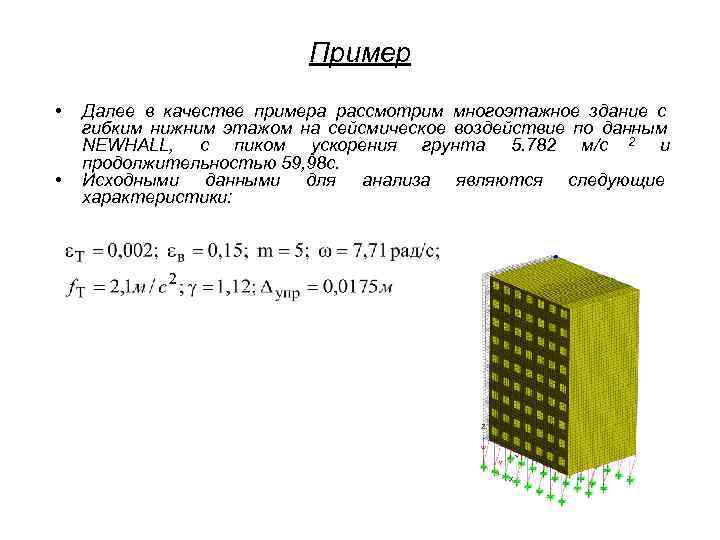
 Пример • Далее в качестве примера рассмотрим многоэтажное здание с гибким нижним этажом на сейсмическое воздействие по данным NEWHALL, с пиком ускорения грунта 5. 782 м/с 2 и продолжительностью 59, 98 с. • Исходными данными для анализа являются следующие характеристики:
Пример • Далее в качестве примера рассмотрим многоэтажное здание с гибким нижним этажом на сейсмическое воздействие по данным NEWHALL, с пиком ускорения грунта 5. 782 м/с 2 и продолжительностью 59, 98 с. • Исходными данными для анализа являются следующие характеристики:
 Анализ системы с гибким нижним этажом • После решения динамической задачи (с помощью программного комплекса Mathcad ) было найдено значение максимального перемещения одностепенной модели, равное Рис. 3. Циклическая диаграмма деформирования одностепенной модели • Далее, используя понятие эквивалентной консоли, были определены значения перемещений в колоннах гибкого этажа и найдено D= 0, 156 м. Следовательно, значение коэффициента пластичности рассмотренной системы равно
Анализ системы с гибким нижним этажом • После решения динамической задачи (с помощью программного комплекса Mathcad ) было найдено значение максимального перемещения одностепенной модели, равное Рис. 3. Циклическая диаграмма деформирования одностепенной модели • Далее, используя понятие эквивалентной консоли, были определены значения перемещений в колоннах гибкого этажа и найдено D= 0, 156 м. Следовательно, значение коэффициента пластичности рассмотренной системы равно
 Расчет на малоцикловую усталость • Уровень деформации, соответствующий данному значению коэффициента пластичности, равен • Исходными данными для расчета на малоцикловую усталость являются следующие характеристики: • Используя формулу, установим связь между характеристиками сопротивления малоцикловой усталости и пластичностью материала при статическом нагружения. • Таким образом, при
Расчет на малоцикловую усталость • Уровень деформации, соответствующий данному значению коэффициента пластичности, равен • Исходными данными для расчета на малоцикловую усталость являются следующие характеристики: • Используя формулу, установим связь между характеристиками сопротивления малоцикловой усталости и пластичностью материала при статическом нагружения. • Таким образом, при
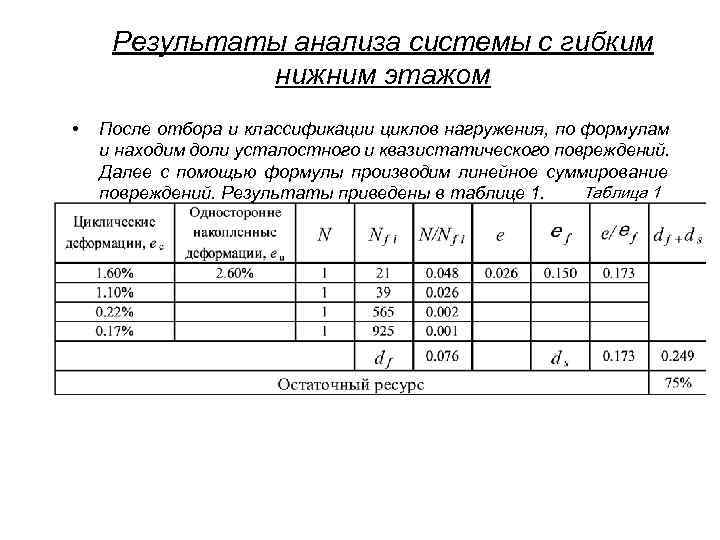
 Результаты анализа системы с гибким нижним этажом • После отбора и классификации циклов нагружения, по формулам и находим доли усталостного и квазистатического повреждений. Далее с помощью формулы производим линейное суммирование повреждений. Результаты приведены в таблице 1. Таблица 1
Результаты анализа системы с гибким нижним этажом • После отбора и классификации циклов нагружения, по формулам и находим доли усталостного и квазистатического повреждений. Далее с помощью формулы производим линейное суммирование повреждений. Результаты приведены в таблице 1. Таблица 1
 Колебательные процессы, происходящие при обтекании длинных структур ветром. Применение программных комплексов CFD
Колебательные процессы, происходящие при обтекании длинных структур ветром. Применение программных комплексов CFD
 Физическое моделирование ветрового воздействия на сооружение 1. Получение общей картины обтекания. Поля значений аэродинамических 2. Определение аэродинамических коэффициентов для фасада здания Наветренная Подветренная коэффициентов для сложных форм. 0, 8 -0, 6 Аэродинамические коэффициенты (СНи. П 2. 01. 07 -85) Плоские сплошные конструкции C Наветренные 0, 8 Подветренные -0, 6 Проблемы применения аэродинамических труб 1. Необходимость создания макета сооружения с оснащением его датчиками для статических и динамических измерений. 2. Использование макетов в уменьшенном масштабе, применение закона подобия. 3. Создание крупных макетов и их испытания в трубах большого диаметра является сложной и дорогостоящей работой.
Физическое моделирование ветрового воздействия на сооружение 1. Получение общей картины обтекания. Поля значений аэродинамических 2. Определение аэродинамических коэффициентов для фасада здания Наветренная Подветренная коэффициентов для сложных форм. 0, 8 -0, 6 Аэродинамические коэффициенты (СНи. П 2. 01. 07 -85) Плоские сплошные конструкции C Наветренные 0, 8 Подветренные -0, 6 Проблемы применения аэродинамических труб 1. Необходимость создания макета сооружения с оснащением его датчиками для статических и динамических измерений. 2. Использование макетов в уменьшенном масштабе, применение закона подобия. 3. Создание крупных макетов и их испытания в трубах большого диаметра является сложной и дорогостоящей работой.
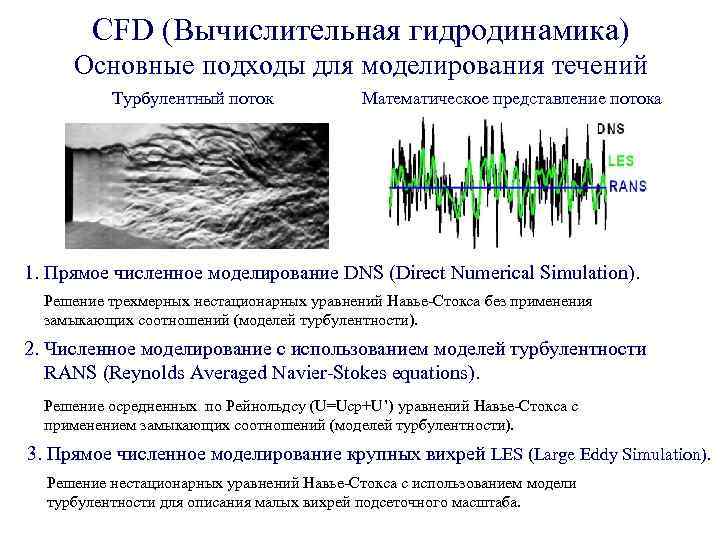
 CFD (Вычислительная гидродинамика) Основные подходы для моделирования течений Турбулентный поток Математическое представление потока 1. Прямое численное моделирование DNS (Direct Numerical Simulation). Решение трехмерных нестационарных уравнений Навье-Стокса без применения замыкающих соотношений (моделей турбулентности). 2. Численное моделирование с использованием моделей турбулентности RANS (Reynolds Averaged Navier-Stokes equations). Решение осредненных по Рейнольдсу (U=Uср+U’) уравнений Навье-Стокса с применением замыкающих соотношений (моделей турбулентности). 3. Прямое численное моделирование крупных вихрей LES (Large Eddy Simulation). Решение нестационарных уравнений Навье-Стокса с использованием модели турбулентности для описания малых вихрей подсеточного масштаба.
CFD (Вычислительная гидродинамика) Основные подходы для моделирования течений Турбулентный поток Математическое представление потока 1. Прямое численное моделирование DNS (Direct Numerical Simulation). Решение трехмерных нестационарных уравнений Навье-Стокса без применения замыкающих соотношений (моделей турбулентности). 2. Численное моделирование с использованием моделей турбулентности RANS (Reynolds Averaged Navier-Stokes equations). Решение осредненных по Рейнольдсу (U=Uср+U’) уравнений Навье-Стокса с применением замыкающих соотношений (моделей турбулентности). 3. Прямое численное моделирование крупных вихрей LES (Large Eddy Simulation). Решение нестационарных уравнений Навье-Стокса с использованием модели турбулентности для описания малых вихрей подсеточного масштаба.
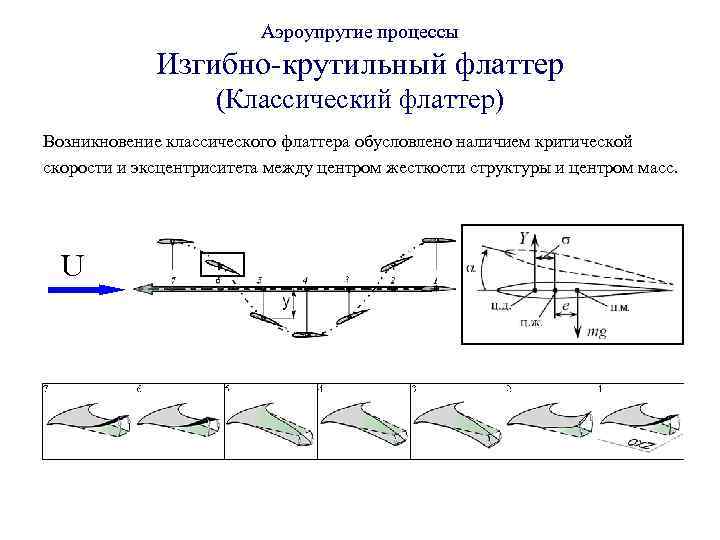
 Аэроупругие процессы Изгибно-крутильный флаттер (Классический флаттер) Возникновение классического флаттера обусловлено наличием критической скорости и эксцентриситета между центром жесткости структуры и центром масс. U
Аэроупругие процессы Изгибно-крутильный флаттер (Классический флаттер) Возникновение классического флаттера обусловлено наличием критической скорости и эксцентриситета между центром жесткости структуры и центром масс. U
 Срывной флаттер представлен в виде Динамическая система с 1 -ой нестационарного движения твердого тела с одной степенью свободы: U F Используя эмпирическую модель для определения силы F вышеприведенное уравнение можно записать в виде: , где D – размер проекции цилиндра на плоскость. . CL определяется из уравнения Ван-дер-Поля: , U y где a 1, …, a 4 – постоянные величины, определяемые экспериментальным путем.
Срывной флаттер представлен в виде Динамическая система с 1 -ой нестационарного движения твердого тела с одной степенью свободы: U F Используя эмпирическую модель для определения силы F вышеприведенное уравнение можно записать в виде: , где D – размер проекции цилиндра на плоскость. . CL определяется из уравнения Ван-дер-Поля: , U y где a 1, …, a 4 – постоянные величины, определяемые экспериментальным путем.
 Срывной флаттер Частота срыва вихры Ns определяется формулой Струхаля: Ns*D/V=Sh где D – поперечный размер сечения обдуваемой структуры V – скорость ветрового потока Sh – число Струхаля
Срывной флаттер Частота срыва вихры Ns определяется формулой Струхаля: Ns*D/V=Sh где D – поперечный размер сечения обдуваемой структуры V – скорость ветрового потока Sh – число Струхаля
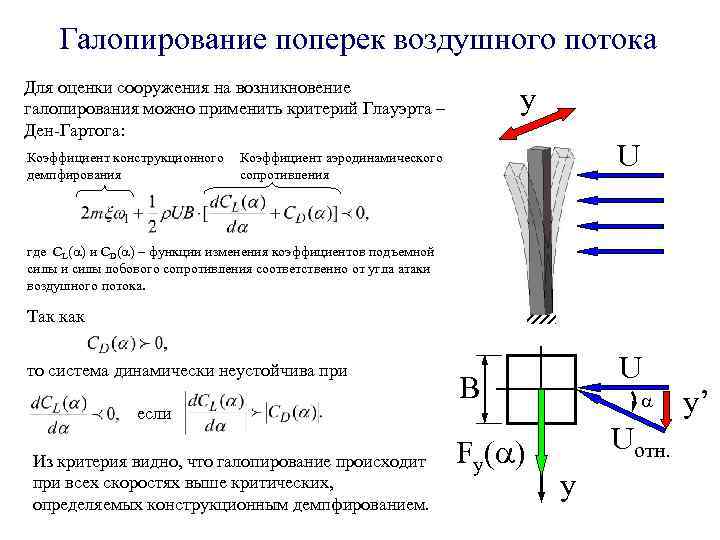
 Галопирование поперек воздушного потока Для оценки сооружения на возникновение галопирования можно применить критерий Глауэрта – y Ден-Гартога: Коэффициент конструкционного демпфирования Коэффициент аэродинамического сопротивления U где CL( ) и CD( ) – функции изменения коэффициентов подъемной силы и силы лобового сопротивления соответственно от угла атаки воздушного потока. Так как то система динамически неустойчива при U B y’ если Fy( ) Uотн. Из критерия видно, что галопирование происходит при всех скоростях выше критических, определяемых конструкционным демпфированием. y
Галопирование поперек воздушного потока Для оценки сооружения на возникновение галопирования можно применить критерий Глауэрта – y Ден-Гартога: Коэффициент конструкционного демпфирования Коэффициент аэродинамического сопротивления U где CL( ) и CD( ) – функции изменения коэффициентов подъемной силы и силы лобового сопротивления соответственно от угла атаки воздушного потока. Так как то система динамически неустойчива при U B y’ если Fy( ) Uотн. Из критерия видно, что галопирование происходит при всех скоростях выше критических, определяемых конструкционным демпфированием. y
 Колебания структуры, вызванные турбулентным потоком (Ветровой резонанс) Алгоритм решения 1. Определение спектра собственных колебаний структуры: 2. Решение уравнения движения, в правой части которого спектральная плотность мощности (спектр Давенпорта) и получение спектра ответа (перемещения, скорости, ускорения): Структура Турбулентный поток Собственные формы Спектральная плотность 3. Определение среднеквадратического отклонения структуры из спектра ответа: Смотри рекомендации по уточненному динамическому расчету зданий и сооружений на действие пульсационной составляющей ветровой нагрузки (утверждены Научно-техническим Советом ЦНИИСК 15 декабря 1999 г. )
Колебания структуры, вызванные турбулентным потоком (Ветровой резонанс) Алгоритм решения 1. Определение спектра собственных колебаний структуры: 2. Решение уравнения движения, в правой части которого спектральная плотность мощности (спектр Давенпорта) и получение спектра ответа (перемещения, скорости, ускорения): Структура Турбулентный поток Собственные формы Спектральная плотность 3. Определение среднеквадратического отклонения структуры из спектра ответа: Смотри рекомендации по уточненному динамическому расчету зданий и сооружений на действие пульсационной составляющей ветровой нагрузки (утверждены Научно-техническим Советом ЦНИИСК 15 декабря 1999 г. )

