Курс лекций МТФ 2 -3 курс Теплоёмкость

Курс лекций (МТФ, 2 -3 курс) Теплоёмкость

Физическую химию трактуют как науку, объясняющую химические явления и устанавливающую их закономерности на основе общих принципов физики. Разделы физической химии: §Строение вещества (химическая связь, структура молекул, химические свойства – рассматривались ранее в курсе неорганической химии) §Химическая термодинамика ( «состояние» ) §Химическая кинетика ( «процесс» ) §Поверхностные явления, адсорбция и катализ §Электрохимия 2

1) 2) 3) 4) Основные вопросы: установление условий равновесия различных химических веществ и различных фаз вещества; выяснение возможности протекания химической реакции или фазового превращения при определенных условиях; определение энергетических эффектов (количеств теплоты и работы) химических реакций и фазовых превращений; разработка методов определения свойств веществ, необходимых для решения отмеченных выше задач. 3

ü ü ü являются альтернативой дорогостоящему эксперименту; позволяют сократить материальные и временные затраты при разработке новых материалов и технологических схем; предсказывают поведение веществ при очень высоких (или низких) температурах и давлениях, в агрессивных средах, в различных силовых полях. Области, использующие результаты термодинамического прогноза: Ø Ø Ø металлургия; нефтехимия; неорганический и органический синтез; получение функциональных и конструкционных маериалов; очистка лекарственных препаратов. 4

q Основные понятия химической термодинамики q Нулевой и первый законы термодинамики q Тепловые эффекты q Закон Гесса. q Зависимость теплового эффекта от температуры 5

в зависимости от фазового состава • гомогенная (только одна фаза – газ, жидкость или кристалл) • гетерогенная (Ф≥ 2) Число (независимых) компонентов: К = c – r – b H 2, O 2, H 2 O: c = 3 (число видов веществ или сортов частиц) H 2, O 2, H 2 O: r = 1 (число уравнений реакций) 2 H 2 + O 2 ↔ 2 H 2 O K = 2 (3) b = 0 (число возможных уравнений связи) v H 22 O, Na. Cl, Na+, Cl--: : c = 4 H O, Na. Cl, Na +, Cl + K = 2 r = 1 Na + Cl ↔ Na. Cl b = 1 n(Na+) = n(Cl-) v в зависимости от способности взаимодействовать с внешней средой • открытая (обменивается энергией и веществом с окружающей средой) • закрытая (обменивается энергией, но нет обмена веществом) • изолированная (нет обмена ни энергией, ни веществом) • адиабатная (граница не пропускает теплоту, нет теплообмена с другими системами) 6

Количественно характеризуют термодинамическую систему Термодинамические параметры – фиксированы условиями существования системы • внешние – определяются свойствами и обобщенными координатами системы в окружающей среде и зависят от контактов системы с окружением: m, n, напряженность электрического поля E (число ограничено); • внутренние – характеризуют свойства системы: плотность ρ, внутренняя энергия U (число неограниченно); • интенсивные – не зависят от массы системы или числа частиц: температура Т, плотность ρ, давление р; обобщенные силы характеризуют состояние равновесия (p, μ, φ, σ); • экстенсивные – прямо пропорциональны массе системы или числу частиц: объем V, энергия U, энтропия S, теплоемкость C; обобщенные координаты изменяются под действием соответствующих обобщенных сил (V, n, e, Ω). Способы выражения состава: 1. числом молей ni каждого из составляющих системы 2. числом молярных долей составляющих: xi = ni / Σni 3. парциальными давлениями газообразных составляющих: pi = xi·p 4. молярными объемными концентрациями (моль/л, кмоль/м 3): ci = ni / V, pi = ci·R·T 5. массовыми долями составляющих: ωi = mi / Σmi, ωi = xi·Mi / Σxi·Mi 7

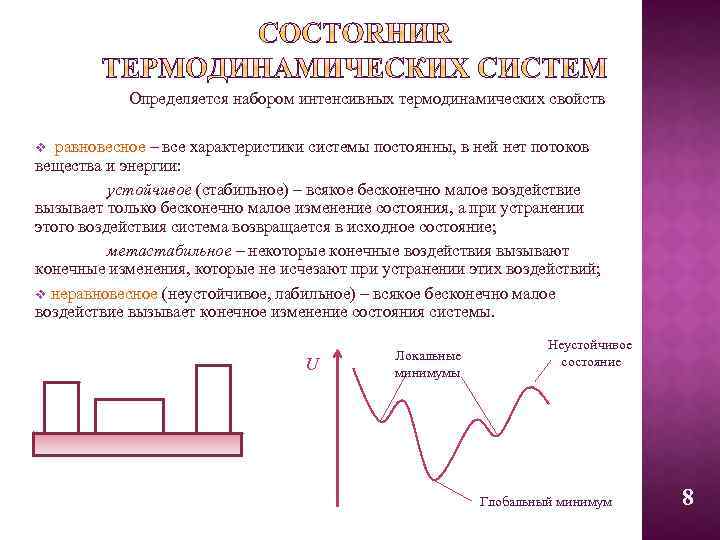Определяется набором интенсивных термодинамических свойств v равновесное – все характеристики системы постоянны, в ней нет потоков вещества и энергии: устойчивое (стабильное) – всякое бесконечно малое воздействие вызывает только бесконечно малое изменение состояния, а при устранении этого воздействия система возвращается в исходное состояние; метастабильное – некоторые конечные воздействия вызывают конечные изменения, которые не исчезают при устранении этих воздействий; v неравновесное (неустойчивое, лабильное) – всякое бесконечно малое воздействие вызывает конечное изменение состояния системы. U Локальные минимумы Неустойчивое состояние Глобальный минимум 8

Любое изменение в термодинамической системе, связанное с изменением хотя бы одной из ее термодинамических переменных. Процесс в термодинамике – это последовательность состояний системы, ведущая от одного, начального, набора термодинамических переменных к другому – конечному. v самопроизвольные, для осуществления которых не надо затрачивать энергию; v несамопроизвольные, происходящие только при затрате энергии; v обратимые – переход системы из одного состояния в другое и обратно может происходить через последовательность одних и тех же состояний, и после возвращения в исходное состояние в окружающей среде не остается макроскопических изменений; v квазистатические, или равновесные – происходят под действием бесконечно малой разности обобщенных сил (часто отождествляют с обратимыми); v необратимые, или неравновесные – в результате процесса невозможно возвратить и систему, и ее окружение к первоначальному состоянию. Если в ходе процесса некоторые переменные зафиксированы: • изотермический T = const • изобарный p = const • изохорный V = const • адиабатический Q = 0, δQ = 0 9

Ø функции состояния – зависят только от состояния системы и не зависят от пути, по которому это состояние получено; энергия U, энтальпия H, энергия Гельмгольца F, энергия Гиббса G, энтропия S, объем V, давление p, температура T; характеризуется следующими свойствами: • бесконечно малое изменение функции f является полным дифференциалом ( обозначается df); • изменение функции при переходе из состояния 1 в состояние 2 определяется только этими состояниями: 2 1 ; • в результате любого циклического процесса функция состояния не изменяется: ; Ø функции процесса (или перехода) – значение зависит от пути, по которому происходит изменение состояния системы; теплота Q, работа W. 10

Связывает равновесные внутренние переменные с внешними переменными и температурой или внутренней энергией. В общем виде: f(a, b, T) = 0 или a = a(b, T), где a – набор внутренних параметров, b - совокупность внешних параметров, T – температура. Термическое уравнение: p = p(V, n, T), p – внутренний, V – внешний параметр. Калорическое уравнение: U = U(V, n, T), U – внутренний, V – внешний параметр. Позволяют определить все термодинамические свойства системы и получить ее полное термодинамическое описание Уравнения состояния можно определить экспериментально ! Количество независимых уравнений состояния = ВАРИАНТНОСТИ системы, т. е. числу независимых переменных, достаточных для описания состояния равновесной системы (оно на 1 больше числа внешних переменных). З А К Р Ы Т А Я О Т К Р Ы Т А Я V 2 V K K+1 K+2 11

Идеальный газ – газ, равновесное состояние которого описывается уравнением Клапейрона-Менделеева: p. V = n. RT или p. Vm = RT p – давление (Па); V – объем системы (м 3); T – термодинамическая температура (К); n – число молей газа; R – универсальная газовая постоянная: R = 8, 314 Дж·моль-1·К-1 = 1, 987 кал·моль-1·К-1 = 0, 082 л·атм·моль-1·К-1; Vm = V/n – мольный объём газа. На основании опытов Джоуля было установлено, что при изотермическом расширении идеального газа его внутренняя энергия не зависит от объёма: = 0 T Внутренняя энергия идеального газа зависит только от температуры: U = U(T) 12

Выводы и соотношения термодинамики можно сформулировать на основе двух постулатов (исходных положений) и трех законов (начал) термодинамики. любая изолированная система с течением времени приходит в равновесное состояние и самопроизвольно не может из него выйти. Ограничивает размер систем, которые описывает классическая термодинамика. 13

если система А находится в тепловом равновесии с системой В, а та, в свою очередь, находится в равновесии с системой С, то системы А и С также находятся в тепловом равновесии. Постулат о существовании температуры. Вводится понятие температуры как особой интенсивной переменной, характеризующей состояние теплового равновесия. Закон термического равновесия позволяет однозначно измерять температуру термометром. Идеальный газ – эталонное термометрическое вещество. Принята линейная зависимость объема (термометрического свойства) от температуры при р = const. Начало отсчета температуры – состояние с V = 0. Шкала идеально-газовой температуры (шкала Кельвина). Vк - Vп ΔV V - V tк - tп = Δt = t - t п = const п Δt = 100 V = 0 t 0 = - Vп 100°С ΔV Если состояние с V = 0 принять за начало отсчета температуры, то t = V Vк V - Vп Δt + tп ΔV По шкале относительной температуры (Цельсия) состояние с V = 0 Тп = - t 0 Vп 100 К = ΔV Из опыта Vп/ ΔV = 2, 7315 t, °С Vп tп = 0 tк = 100 V=0 Т = 0 Тк Тп Т, К Тп = 273, 15 + t K 14

Закон сохранения энергии! Утверждает: существует аддитивная функция состояния термодинамической системы, называемая внутренней энергией, U. 1. Внутренняя энергия изолированной системы постоянна. При этом один вид энергии превращается в эквивалентном количестве в другой. ΔU = 0 2. В неизолированной системе она может изменяться за счет: а) совершения работы W над окружающей средой (или среды над системой); б) обмена теплотой Q с окружающей средой. В дифференциальной форме: d. U = δQ – δW; в интегральной : ΔU = Q – W = U 2 – U 1 = ΔU «Тепло, подведенное к системе, тратится на совершение работы и изменение внутренней энергии системы» Q >0 – полученная системой, W>0 совершенная системой. Работа – упорядоченная форма передачи энергии, при совершении работы частицы тела движутся организованно в определенном направлении. Теплота – форма обмена энергией, соответствующая хаотическому, беспорядочному, неорганизованному движению микрочастиц, составляющих систему. Состоит в непосредственной передаче энергии молекулами одного тела молекулам другого. 15

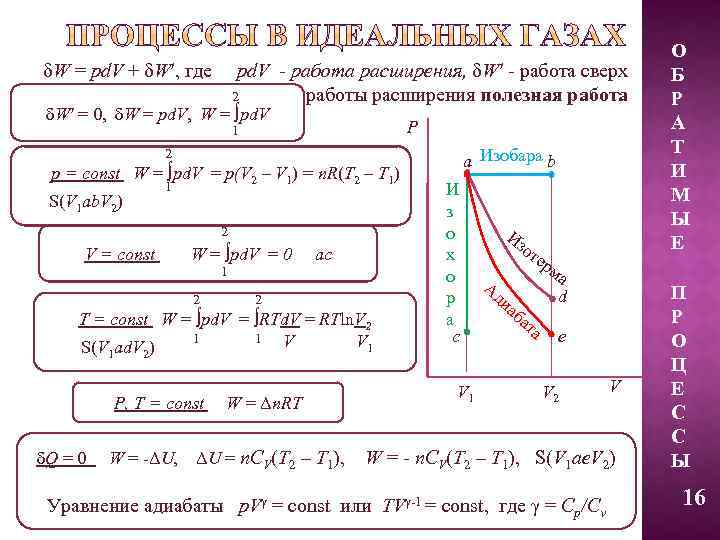δW = pd. V + δW′, где pd. V - работа расширения, δW′ - работа сверх работы расширения полезная работа 2 δW′ = 0, δW = pd. V, W = ∫pd. V P 1 a Изобара b 2 p = const W = ∫pd. V = p(V 2 – V 1) = n. R(T 2 – T 1) 1 S(V 1 ab. V 2) 2 V = const W = ∫pd. V = 0 1 2 ac 2 T = const W = ∫pd. V = ∫RTd. V = RTln. V 2 1 1 V V 1 S(V ad. V ) 1 И з о х о р а c Из от е Ад иа ба рм та а d e 2 P, Т = const W = Δn. RT δQ = 0 W = -ΔU, ΔU = n. CV(T 2 – T 1), V 1 V 2 V W = - n. CV(T 2 – T 1), S(V 1 ae. V 2) Уравнение адиабаты p. Vγ = const или TVγ-1 = const, где γ = Cp/Cv О Б Р А Т И М Ы Е П Р О Ц Е С С Ы 16

δQ = d. U + pd. V V = const , d. V = 0 δQV – является полным дифференциалом: δQV = d. U QV = U 2 – U 1 = ΔU теплота изохорного процесса равна приращению внутренней энергии системы. p = const , pd. V = d(p. V) δQp = d. U + pd. V = d(U + p. V) - является полным дифференциалом. Следовательно, выражению U + p. V соответствует функция состояния, которую называют энтальпией Н (теплосодержанием): Н = U + p. V δQp = d. Н Qр = Н 2 – Н 1 = ΔН теплота изобарного процесса равна приращению энтальпии системы во время этого процесса. При Т = const в системе Qр = QV + pΔV или Qр = QV + Δn. RT Δn – приращение числа молей газообразных веществ в результате протекания химической реакции. С 2 Н 4(г) + Н 2(г) = С 2 Н 6(г) Δn = n. C 2 H 6 – (n. C 2 H 4 + n. H 2) = 1 – (1+1) = – 1 ΔH = ΔU + Δn. RT ΔH – ΔU = – 1· 8, 314· 298 = – 2477 Дж/моль 17

Тепловым эффектом химической реакции называют количество теплоты, выделяемое или поглощаемое в результате осуществления химического процесса в термомеханической системе (δW′ = 0) при постоянном давлении или объеме (p = const, V = const) и равенстве температур исходных веществ и продуктов (Тисх = Тпрод). Термохимия – раздел физической химии, в котором изучают тепловые эффекты химических реакций. Основной экспериментальный метод – калориметрия. Термохимические уравнения Qр = Δr. Н (“reaction”) Экзотермические процессы – выделяется теплота, Δr. Н<0 СН 4 + 2 О 2 → СО 2 + 2 Н 2 О – 890 к. Дж/моль Эндотермические процессы – поглощается теплота, Δr. Н>0 СО 2 + С → 2 СО + 178, 4 к. Дж/моль 18

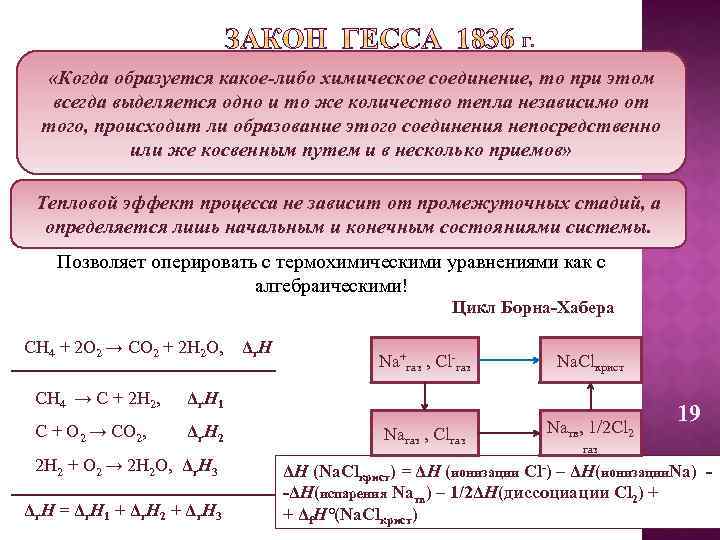«Когда образуется какое-либо химическое соединение, то при этом всегда выделяется одно и то же количество тепла независимо от того, происходит ли образование этого соединения непосредственно или же косвенным путем и в несколько приемов» Тепловой эффект процесса не зависит от промежуточных стадий, а определяется лишь начальным и конечным состояниями системы. Позволяет оперировать с термохимическими уравнениями как с алгебраическими! Цикл Борна-Хабера СН 4 + 2 О 2 → СО 2 + 2 Н 2 О, Δr. Н Na+газ , Cl-газ Na. Clкрист Naгаз , Clгаз Naтв, 1/2 Cl 2 СН 4 → С + 2 Н 2, Δr. Н 1 С + О 2 → СО 2, Δr. Н 2 2 Н 2 + О 2 → 2 Н 2 О, Δr. Н 3 Δr. Н = Δr. Н 1 + Δr. Н 2 + Δr. Н 3 19 газ ΔН (Na. Clкрист) = ΔН (ионизации Cl-) – ΔН(ионизации. Na) -ΔН(испарения Naтв) – 1/2ΔН(диссоциации Cl 2) + + Δf. Н°(Na. Clкрист)

Можно использовать для расчета энтальпий самых разнообразных реакций, исходя из следующих соображений: 1) количество любого из химических элементов, входящих в структуры химических соединений, Исходные вещества сохраняется в ходе реакции; Δr. Н 2) температура проведения процесса постоянна; Δr. Н(нач) 1) 2) 3) 4) Конечные вещества тепловой эффект можно рассчитать, если провести мысленно реакции с начальными и Δr. Н(кон) конечными веществами до одних и тех же Одинаковые продуктов. продукты Если продукты, полученные в реакциях с участием начальных и конечных веществ, представляют собой: простые вещества, то величины Δr. Н(нач) и Δr. Н(кон) представляют собой теплоты образования; продукты сгорания, то Δr. Н(нач) и Δr. Н(кон) – энтальпии процессов сгорания; атомы, то Δr. Н(нач) и Δr. Н(кон) – энергии связи с обратным знаком; молекулы растворенного вещества или ионы в растворах, то Δr. Н(нач) и Δr. Н(кон) – теплоты растворения. 3) Зная стандартные энтальпии образования (сгорания, растворения и т. д. ), рассчитываем изменение энтальпии в самых разнообразных реакциях! 20

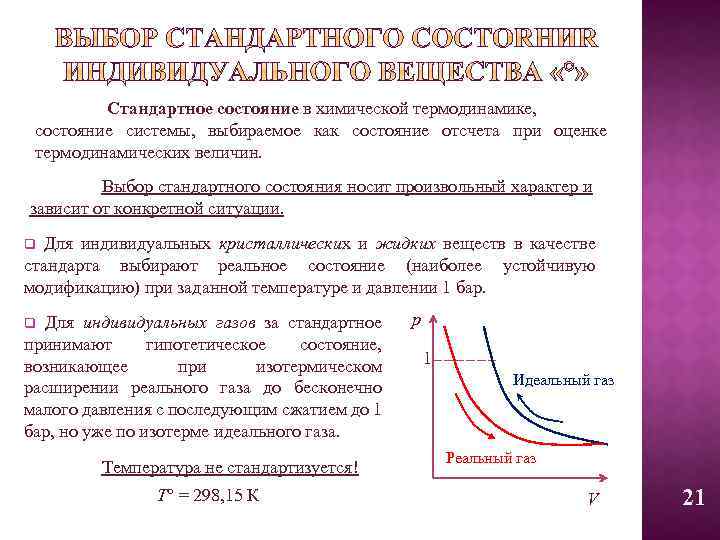Стандартное состояние в химической термодинамике, состояние системы, выбираемое как состояние отсчета при оценке термодинамических величин. Выбор стандартного состояния носит произвольный характер и зависит от конкретной ситуации. q Для индивидуальных кристаллических и жидких веществ в качестве стандарта выбирают реальное состояние (наиболее устойчивую модификацию) при заданной температуре и давлении 1 бар. q Для индивидуальных газов за стандартное принимают гипотетическое состояние, возникающее при изотермическом расширении реального газа до бесконечно малого давления с последующим сжатием до 1 бар, но уже по изотерме идеального газа. Температура не стандартизуется! Т° = 298, 15 К р 1 Идеальный газ Реальный газ V 21

В термохимии используются: v Стандартная энтальпия реакции Δr. H°Т – энтальпия реакции между веществами, находящимися в стандартных условиях при температуре Т. Стандартная энтальпия образования, Δf. H°Т (“formation”) – изобарный тепловой эффект реакции образования одного моля данного химического соединения из простых веществ в стандартных состояниях (ионов). Энтальпия образования простого вещества в стандартном состоянии равна нулю при любой температуре. Δf. H°Т (Н+) = 0. v v Стандартная энтальпия сгорания, Δс. H°Т (“combustion”) – изобарный тепловой эффект реакции окисления одного моля вещества газообразным кислородом при р(О 2) = 1 бар. В качестве продуктов сгорания элементов C, H, N, S и Cl принимают СО 2(г), Н 2 О(ж), N 2(г), SO 2(г) и HCl(г). Теплота сгорания продуктов сгорания равна нулю. 2 Al(тв) + 3/2 O 2(г) = Al 2 O 3(тв), Δf. H°Т Al(тв) + 3/4 O 2(г) = 1/2 Al 2 O 3(тв), Δc. H°Т 22

Интегральная энтальпия растворения – изменение энтальпии в процессе растворения конечного количества вещества в определенном (конечном) количестве растворителя (зависит от концентрации раствора, может быть измерена экспериментально). • Первая интегральная энтальпия растворения – тепловой эффект растворения 1 моля вещества в бесконечно большом количестве растворителя. • Полная энтальпия растворения – энтальпия растворения 1 моля вещества с образованием насыщенного раствора. v Промежуточная энтальпия ΔHm растворения – изменение энтальпии в процессе растворения вещества в его ненасыщенном растворе. v 0 ΔHm ΔH 0 1 m 2 m 1 ΔHm = ΔHm – ΔHm 1 2 v Интегральная энтальпия разведения 0 ΔH m = 1 ΔH 0 – ΔHm v Промежуточная 1 ΔHm 2 0 энтальпия разведения m 1 m 2 m ΔHm 1= ΔHm – ΔHm 2 1 2 ΔHs m 23

24

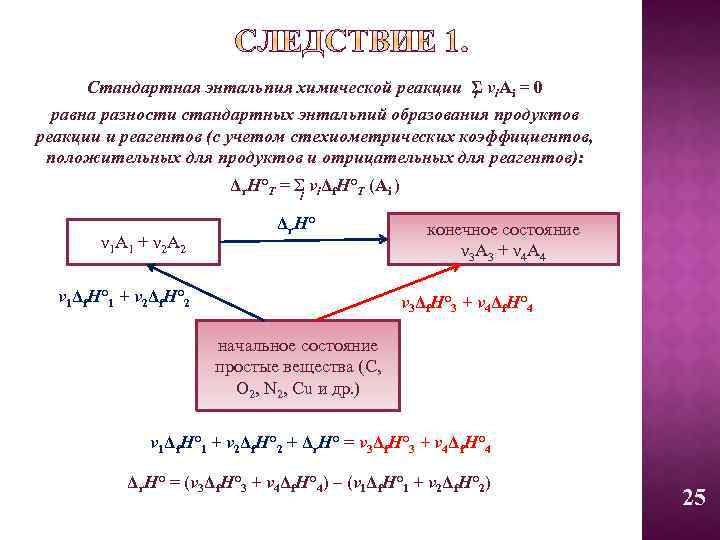Стандартная энтальпия химической реакции Σ νi. Ai = 0 i равна разности стандартных энтальпий образования продуктов реакции и реагентов (с учетом стехиометрических коэффициентов, положительных для продуктов и отрицательных для реагентов): Δr. H°Т = Σ νiΔf. H°Т (Ai ) i ν 1 A 1 + ν 2 A 2 Δr. H° ν 1Δf. H° 1 + ν 2Δf. H° 2 конечное состояние ν 3 A 3 + ν 4 A 4 ν 3Δf. H° 3 + ν 4Δf. H° 4 начальное состояние простые вещества (C, O 2, N 2, Cu и др. ) ν 1Δf. H° 1 + ν 2Δf. H° 2 + Δr. H° = ν 3Δf. H° 3 + ν 4Δf. H° 4 Δr. H° = (ν 3Δf. H° 3 + ν 4Δf. H° 4) – (ν 1Δf. H° 1 + ν 2Δf. H° 2) 25

Стандартная энтальпия химической реакции Σ νi. Ai = 0 i равна разности стандартных энтальпий сгорания реагентов и продуктов реакции (с учетом стехиометрических коэффициентов): Δr. H°Т = Σ νiΔс. H°Т (Ai ) i начальное состояние ν 1 A 1 + ν 2 A 2 ν 1Δс. H° 1 + ν 2Δс. H° 2 Δr. H° + n. O 2(г) ν 3 A 3 + ν 4 A 4 + n. O 2(г) ν 3Δс. H° 3 + ν 4Δс. H° 4 конечное состояние продукты сгорания (СО 2(г), Н 2 О(ж), N 2(г), SO 2(г), HCl(г) и др. ) ν 1Δс. H° 1 + ν 2Δс. H° 2 = Δr. H° + ν 3Δс. H° 3 + ν 4Δс. H° 4 Δr. H° = (ν 1Δс. H° 1 + ν 2Δс. H° 2) – (ν 3Δс. H° 3 + ν 4Δс. H° 4) 26

Энтальпия химической реакции равна разности энергий разрываемых и образующихся химических связей. Энергией связи А – В называют энергию, необходимую для разрыва связи и разведения образующихся частиц на бесконечное расстояние: АВ(г) → А(г) + В(г). Энергия связи всегда положительна. Приближенно теплоты образования газообразных органических соединений можно рассчитать по формуле: Δf. H° = Σνисхεисх + νс. Qcвозг – Σνпрεпр Δf. H° - теплота образования; Σνисхεисх – сумма средних энергий связи в молекулах исходных веществ; νс. Qcвозг – теплота возгонки νс молей углерода (графита); Σνпрεпр – сумма средних энергий связи в молекулах продуктов реакции. 27

28 Можно определить: v теплоты фазовых превращений Δисп. H° = Δf. H°газ – Δf. H°ж Δвозг. H° = Δf. H°газ – Δf. H°тв Δпл. H° = Δf. H°ж – Δf. H°тв Δвозг. H° = Δпл. H° + Δисп. H° v теплоты образования вещества в растворе Δf. H°aq = Δf. H° – ΔHm Теплоты образования ионов обычно относят к бесконечному разведению: S(тв) + O 2(г) + 2 e + ∞H 2 O → SO 4 -aq Применение закона Гесса к реакциям нейтрализации сильных кислот сильными основаниями при записи этих реакций в ионной форме показывает, что тепловой эффект всех этих реакций не зависит от природы кислот и щелочей, а определяется тепловым эффектом процесса: Н+aq + ОН-aq = Н 2 О Δr. H°нейтр = Δf. H°(Н 2 О) – Δf. H°(ОН-) – Δf. H°(Н+) = – 285, 84 + 229, 94 = – 55, 9 к. Дж/моль Нейтрализация слабых кислот сильными основаниями или сильных кислот слабыми основаниями сопровождается одновременной диссоциацией слабого электролита. Δr. H°нейтр = – 55, 9 к. Дж/моль + ΔH°дисс

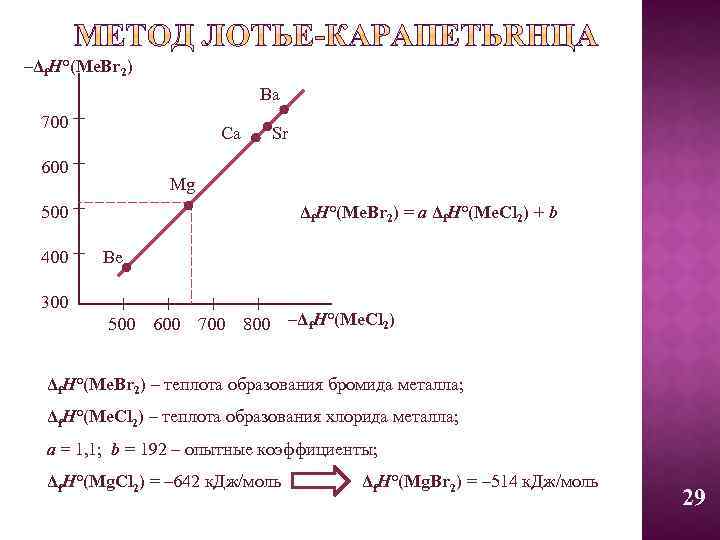–Δf. H°(Me. Br 2) Ba 700 Ca 600 Mg Δf. H°(Me. Br 2) = a Δf. H°(Me. Cl 2) + b 500 400 300 Sr Be 500 600 700 800 –Δf. H°(Me. Cl 2) Δf. H°(Me. Br 2) – теплота образования бромида металла; Δf. H°(Me. Cl 2) – теплота образования хлорида металла; a = 1, 1; b = 192 – опытные коэффициенты; Δf. H°(Mg. Cl 2) = – 642 к. Дж/моль Δf. H°(Mg. Br 2) = – 514 к. Дж/моль 29

Для реакции Σ νi. Ai = 0. Если количество вещества Ak в результате протекания реакции на некоторую глубину изменится на величину Δn(Ak), то количество другого, например i-го, изменится на величину Δn(Ai) = Δn(Ak)·νi/νk. Видно, что Δn(Ai)/νi = Δn(Ak)/νk. Отношение изменения количества любого вещества, участвующего в реакции, к величине стехиометрического коэффициента, стоящего при химической формуле этого же вещества в уравнении реакции, не зависит от взятого вещества, а определяется только глубиной протекания реакции. Химическая переменная ξ = Δn(Ai)/νi (стехиометрические коэффициенты положительны для продуктов и отрицательны для исходных веществ) Характеризует глубину протекания процесса. Переменная де Донде, степень протекания(или полноты) реакции, координата реакции, число пробегов реакции. 30

31 При проведении процесса при условиях V = const или р = const для выполнения закона Гесса необходимо еще одно условие Т = const. В указанных условиях изменение количества теплоты происходит благодаря изменению химической переменной, т. е. количеств отдельных веществ, участвующих в реакции. Под величинами, характеризующими изменение теплоты в химических процессах, QV или Qp, и имеющими размерность к. Дж/моль, следует понимать и Т, V соответственно. Т, р N 2 + 3 H 2 = 2 NH 3 Δn(H 2) = – 1 моль Δn(N 2) = – 1/3 моля ξ = 1/3 моля Δn(NH 3) = +2/3 моля Δr. H° 298 = – 91, 88 к. Дж/моль·(1/3)моль = – 30, 63 к. Дж 1/2 N 2 + 3/2 H 2 = NH 3 Δn(H 2) = – 1 моль Δn(N 2) = – 1/3 моля ξ = 2/3 моля Δn(NH 3) = +2/3 моля Δr. H° 298 = – 45, 94 к. Дж/моль·(2/3)моль = – 30, 63 к. Дж Изменение термодинамических функций в процессе не зависит от выбранных стехиометрических коэффициентов и определяется только изменением реального количества (числа молей) реагентов.

Теплоемкость – количество теплоты, необходимое для того, чтобы повысить температуру системы на определенную величину (обычно на 1 градус) Теплоемкость – экспериментально измеряемая экстенсивная величина (адиабатическая калориметрия). Истинная теплоемкость Средняя теплоемкость – количество теплоты, которое надо сообщить веществу, чтобы нагреть его на 1 К. С= С= 2 1 Зависит от способа осуществления процесса нагревания Изохорная теплоемкость (V = const) Изобарная теплоемкость (p = const) СV = Cp = V = p p = V V ≈ ≈ p = V Если С, С, СV , Сp [Дж·К-1] относятся к одному молю вещества, то говорят о мольных значениях теплоемкости Сm [Дж·моль-1·К-1]. 32

В общем виде: Cp – CV = T· · p находят дифференцированием графиков функций V = f(T) и p = f(T), которые получают по опытным данным или аналитически, если известны уравнения состояния. и V p Cp = V = p p = +p p p По закону Джоуля, внутренняя энергия идеального газа является функцией только температуры. Поэтому = = CV V = p V подставляем в p Сp = C V + R Согласно молекулярно-кинетической теории газов для 1 моля идеального газа : CV = 3/2 R, Cp = 5/2 R – для одноатомных газов; CV = 5/2 R, Cp = 7/2 R – для двухатомных газов и т. д. 33

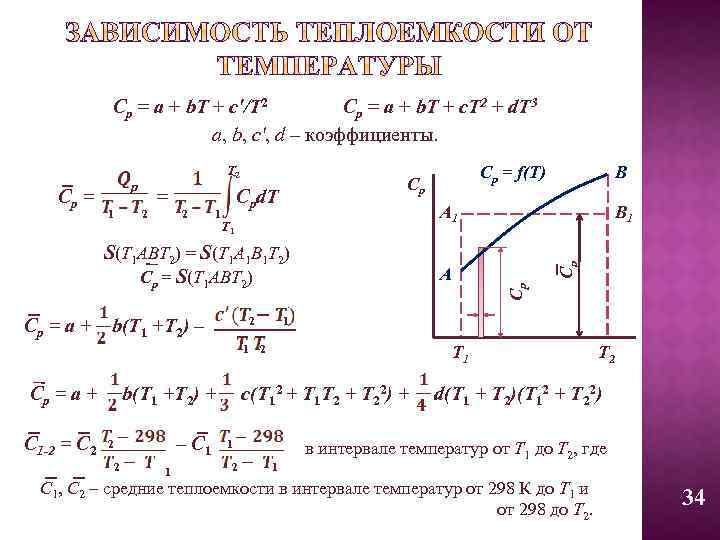Cp = a + b. T + c'/T 2 Cp = a + b. T + c. T 2 + d. T 3 a, b, c', d – коэффициенты. T 2 Ср = f(T) Ср Cp = Cpd. T 1 2 2 1 А 1 p В В 1 Cp = a + 2 b(T 1 +T 2) – А 1 1 2 Cp = a + C 1 -2 = C 2 b(T 1 +T 2) + – C 1 2 2 1 Т 1 c(T 12 + T 1 T 2 + T 22) + 1 2 Ср S(T 1 ABT 2) = S(T 1 A 1 B 1 T 2) Cp = S(T 1 ABT 2) Ср T 1 1 Т 2 d(T 1 + T 2)(T 12 + T 22) в интервале температур от Т 1 до Т 2, где С 1, С 2 – средние теплоемкости в интервале температур от 298 К до Т 1 и от 298 до Т 2. 34

Для расчета стандартных тепловых эффектов r. HT° = Δr. Cp при Т ≠ 298 К используют уравнение Кирхгофа в T 2 дифференциальной Δr. HT° = Δr. HT° + Δr. Cp(T)d. T, где или интегральной форме 2 1 под знаком интеграла стоит разность изобарных теплоемкостей продуктов реакции и исходных веществ. Если разность (Т 2 – Т 1) невелика, то можно принять T 1 Δr. Cp = Σνi. Cp(Ai) i Δr. Cp = const. Чтобы установить характер изменения теплового эффекта при изменении температуры производят математический анализ дифференциальной формы ΔН H α 1 Ср > 0 α 1 ΔН > 0 Ср = 0 0 Ср < 0 ΔН < 0 Т 1 Т = tgα 1 – угол между касательной, проведенной к кривой ΔН(Т) в точке Т 1 и положительным направлением оси абсцисс. ΔCp = tgα 35

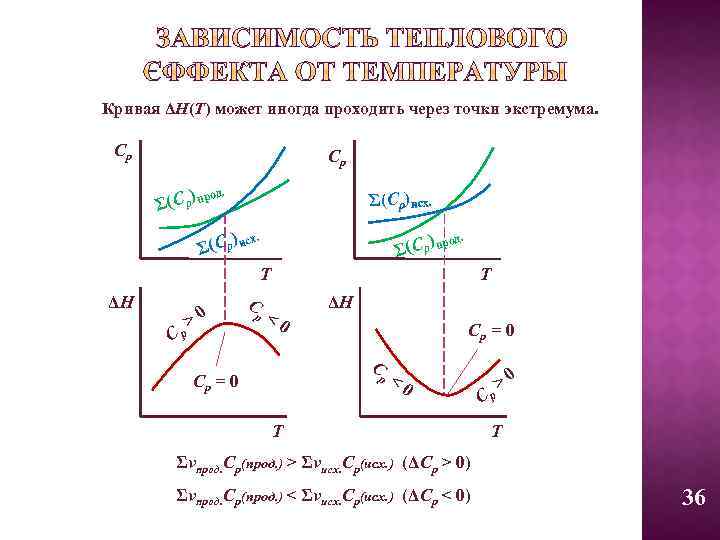Кривая ΔН(Т) может иногда проходить через точки экстремума. Ср Ср д. (С р) про Σ Σ(Ср)исх. ) сх. Σ (С р и д. (С р) про Σ Т ΔН Ср >0 С р Т <0 ΔН Ср = 0 С р Ср = 0 <0 Т Ср >0 Т Σνпрод. Ср(прод. ) > Σνисх. Ср(исх. ) (ΔСр > 0) Σνпрод. Ср(прод. ) < Σνисх. Ср(исх. ) (ΔСр < 0) 36

Cp = a + b. T + c. T 2 + c'/T 2, тогда Δr. Cp = Δa + Δb. T + Δc. T 2 + Δc'/T 2, где Δa, Δb, Δс, Δc' – термодинамические суммы соответствующих коэффициентов, которые вычисляются Δa = Σνпрод. aпрод. – Σνисх. aпрод. и т. д. После подстановки в уравнение Кирхгофа и интегрирования получаем: Δr. HT° = Δr. H 298° + Δa(T - 298) + (T 2 – 2982) + (T 3 – 2983) – Δc'( – ) 37

Количество тепла, поглощенного при нагревании тела от Т 1 до Т 2, связано со средней теплоемкостью: T 2 Qp = Cpd. T = Cp(T 2 – T 1) T 1 Для реакции, совершившей один пробег, можно записать: T 2 Δ Cpd. T = ΔCp(T 2 – T 1) T 1 T 2 или ΔCpd. T = ΔCp(T 2 – T 1) T 1 Подставляя в уравнение Кирхгофа и полагая, что Т = 298 К, получим: Δr. HT° = Δr. H 298° + ΔCp(T – 298) 38

Для реакций, протекающих в газовой фазе при высоких температурах. T HT° - H 0° - значения (в таблицах) высокотемпературных составляющих HT° - H 0° = Cpd. T Cp = p 0 H 0° - гипотетическое значение энтальпии тела в состоянии идеального газа при 0 К в стандартных условиях; Cp – теплоемкость тела в газообразном состоянии. При 0 К реальные тела находятся в твердом агрегатном состоянии, при нагревании от 0 К до высокой температуры будут происходить фазовые превращения тела: плавление и испарение. В связи с этим абсолютная энтальпия газа при температуре Т равна: Tпл Tк T HT° = H 0°тв + Cp твd. T + ΔНпл + Cp жd. T + ΔНк + Cp газd. T 0 Tпл Tк Tк T HT° - (H 0°тв + ΔНпл + ΔНк )= Cp твd. T + Cp жd. T + 0 Tпл или Cp газd. T H 0°газ = H 0°тв + ΔНпл + ΔНк Tк Если реакция совершает один пробег: Δ(HT° - H 0°) = Σνпрод(HT° - H 0°)прод - Σνисх(HT° - H 0°)исх Δr. HТ = Δ(HT° - H 0°) + ΔH 0° - гипотетический тепловой эффект реакции при 0 К (вычисляется по первому следствию из закона Гесса с применением Δf. H 0°). 39