КУРС ЛЕКЦИЙ АЭРОДИНАМИКА-1 АЭРОДИНАМИЧЕСКОЕ ПРОЕКТИРОВАНИЕ 54 аудиторных часа

КУРС ЛЕКЦИЙ АЭРОДИНАМИКА-1, АЭРОДИНАМИЧЕСКОЕ ПРОЕКТИРОВАНИЕ 54 аудиторных часа (лекции) Курсовой проект (самостоятельно)

ЛЕКЦИЯ 1 4. 1. Основные геометрические параметры крыла Крыло является основной несущей поверхностью ЛА и служит для создания подъем ной силы. Аэродинамические свойства крыла определяются в значительной степени его формой и размерами (рис. 4. 1). Рис. 4. 1. Геометрические характеристики крыла

Геометрическая форма крыла характеризуется его профилем, формой в плане, попе речной формой и закрученностью. Рассечем крыло плоскостью А-А, параллельной его плоскости. Контур сечения образует фигуру, называемую профилем крыла в данном сечении. Линия, соединяющая наиболее удаленные точки профиля (носик и хвостик), называется хордой профиля и обозначается b. Совместим с хордой профиля ось Ох прямоугольной системы координат Оху. Тогда форма профиля описывается координатами его верхней и нижней дужек ув = f(х), ун = f(х). Средней линией профиля называется линия, описываемая уравне нием Разность координат (ув – ун) представляет собой толщину профиля в рассматривае мой точке хорды. Одним из основных геометрических параметров профиля является максимальное значение его толщины. Ее положение на хорде характеризуется расстоянием. Вогнутостью профиля называется расстояние от средней линии до хорды. Максимальное значение вогнутости обозначается f, а ее положение на хорде опреде ляется координатой. Важной характеристикой профиля является радиус закругле ния носка r, т. е. радиус вписанной в носок профиля окружности.

Обычно рассматриваются безразмерные параметры профиля: – относительная толщина профиля (0. 03… 0. 18); – относительная координата точки с максимальной относительной толщиной (0. 3… 0. 5); – относительная вогнутость или кривизна (0… 0. 02); – относительная координата точки с максимальной вогнутостью (0. 3… 0. 4); – относительный радиус закругления носка (0… 0. 03). Все крыловые профили объединены в серии. Каждая серия имеет определенные законы изменения толщины и вогнутости вдоль хорды. Форму крыла в плане характеризует проекция крыла на плоскость хорд. Наиболее простую форму в плане имеют крылья с прямолинейными кромками: прямоугольные, трапециевидные, стреловидные и треугольные.

Рис. 4. 2. Различные виды крыльев в плане Размеры крыла характеризуются размахом l, корневой b 0 и концевой bк хордами. Площадь крыла равна: , где – средняя геометрическая хорда крыла.

Форма в плане крыльев с прямолинейными кромками определяется тремя безразмер ными параметрами: удлинение сужение угол стреловидности χ. Удлинение, сужение и угол стреловидности крыльев современных ЛА колеблются в широких пределах (0. 5 < λ < 20). У прямоугольных крыльев η = 1 и χ = 0, у треуголь ных крыльев η = 0. В настоящее время широко применяются крылья сложной формы в плане: а) – с изломом передней кромки; б) – с переменным углом стреловидности по передней кромке; в) – с изменяемой в полете стреловидностью.

Рис. 4. 3. Сложные в плане крылья Закрученность крыла. Рис. 4. 4. Коническая крутка

4. 2. Системы координат. Аэродинамические силы и моменты. Аэродинамические коэффициенты При изучении аэродинамики крыла наиболее часто используются две прямоуголь ные системы координат: скоростная Оaх уa za и связанная Ох у z. Рис. 4. 5. Скоростная система координат В скоростной системе скоростная ось Охa направлена вдоль вектора скорости полета , ось подъемной силы Оуa перпендикулярна направлению полета и лежит в плоскости симметрии крыла, а боковая ось Оza перпендикулярна первым двум осям и направлена в сторону правого полукрыла.

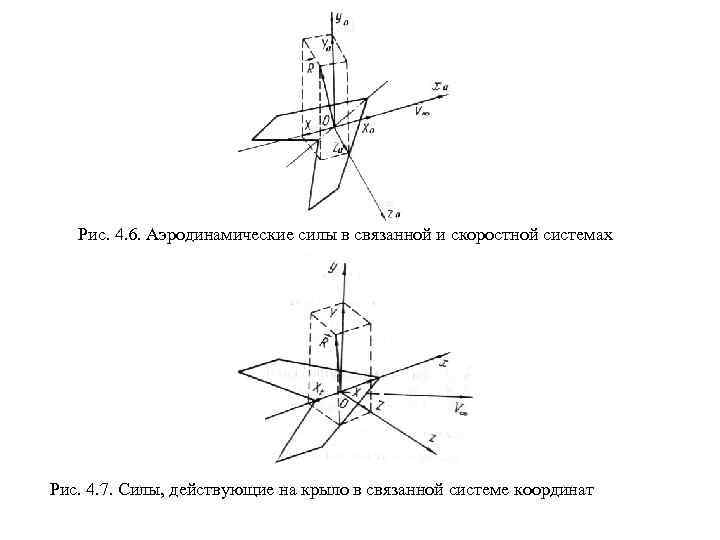Рис. 4. 6. Аэродинамические силы в связанной и скоростной системах Рис. 4. 7. Силы, действующие на крыло в связанной системе координат

Рис. 4. 8. Аэродинамические моменты и их направление Величины аэродинамических сил и моментов зависят от многих факторов: от фор мы и размеров крыла, скорости и высоты углов атаки и скольжения и др. Опыт показывает, что величина аэродинамических сил пропорциональна скоростному напору и некоторой характерной площади S, а величина моментов и еще и характерному линейному размеру (b или l).

В соответствии с этим вводятся безразмерные коэффициенты пропорциональности для сил в скоростной системе координат: – коэффициент лобового сопротивления; – коэффициент подъемной силы; – коэффициент боковой силы. В связанной системе координат: – коэффициент продольной силы; – коэффициент нормальной силы; – коэффициент поперечной силы.

Аналогично вводятся безразмерные коэффициенты пропорциональности для моментов – коэффициент момента крена; – коэффициент момента рысканья; – коэффициент момента тангажа. Между аэродинамическими коэффициентами сил в скоростной и связанной сис темах координат существует связь. Установим ее применительно к случаю β = 0), когда (4. 9) = 0. Пусть заданы коэффициенты сх и су. Тогда на основании

Рис. 4. 9. Связь между системами координат При малых углах атаки ( 0, соs 1, sin ) с достаточной для инженерных расчетов точностью получим В аэродинамике рассматривают характеристики профиля, понимая под ними аэро динамические характеристики крыла бесконечного размаха, имеющего данный профиль.

4. 3. Средняя аэродинамическая хорда крыла Для крыла любой формы можно подобрать эквивалентное прямоугольное крыло такой же площади, имеющее примерно такие же коэффициенты подъемной силы и момента тангажа, как и исходное крыло. Хорду этого прямоугольного крыла и называют средней аэродинамической хордой (САХ). Рис. 4. 10. Эквивалентные крылья Если x(z) и y(z) текущие координаты передней кромки крыла, а b’(z) его хорда теку щего сечения, то для САХ и координат ее передней кромки можно получить следу ющие выражения:

Для крыльев простой формы в плане, геометрическая форма которых определяется удлинением λ, углом стреловидности χ сужением η и поперечным углом ψ, можно получить следующие формулы: Рис. 1. 11. К определению САХ Половина крыла делится на две части простой формы с площадями S 1 и S 2 соот ветственно. Для каждой из них способом, описанным выше, находятся средние аэродинамические хорды b. A 1 и b. A 2. Концы их соединяются прямыми АВ и CD. Полученная трапеция АВСD делится на две части линией так, что В этом случае отрезок MN и является САХ всего крыла.

ЛЕКЦИЯ 2 4. 4. Картина распределения давления Суммарные аэродинамические силы являются результатом действия распределенных по поверхности крыла касательных сил трения и нормальных сил давления. Рассмотрим обтекание некоторого сечения крыла и проанализируем картину распределения давления в этом сечении. (рис. 4. 12). Изменение давления р в рассматриваемой точке крыла при его обтекании по сравнению с давлени ем невозмущенного потока р∞ характеризуется безразмерным коэффициентом давления рис. 4. 12

При плавном обтекании крыла несжимаемым потоком с ростом угла атаки разрежение потока на верхней поверхности происходит в большей степени, чем повышение давления на нижней. Действительно, из уравнения Бернулли для двух сечений струйки для коэффициента давления в несжимаемой среде ( ) получим (4. 4) Следовательно, в критической точке (V = 0) давление ограничено. С другой стороны, разрежение теоретически может происходить до полного вакуума (р = 0), тогда При малых скоростях полета и величина разрежения практически неограниченна, поэтому на малых скоростях основную роль в создании подъемной силы играет разрежение на верхней поверхности крыла. И, наоборот, на больших (особенно сверхзвуковых) скоростях и возрастает роль нижней поверхности в создании подъемной силы.

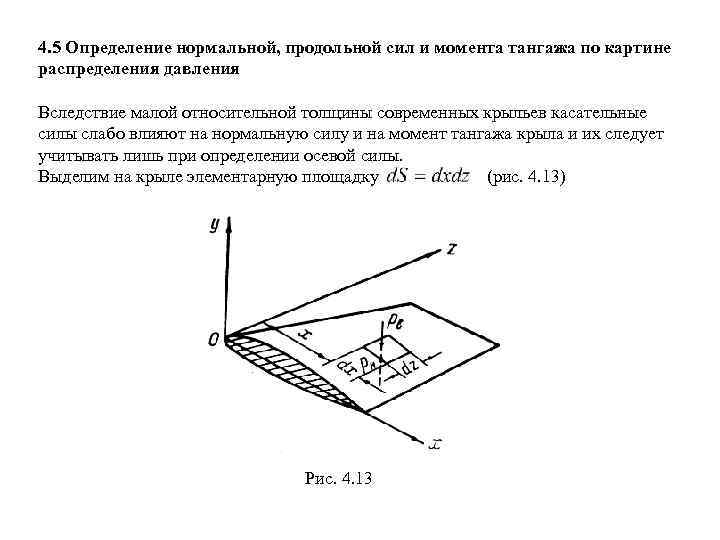4. 5 Определение нормальной, продольной сил и момента тангажа по картине распределения давления Вследствие малой относительной толщины современных крыльев касательные силы слабо влияют на нормальную силу и на момент тангажа крыла и их следует учитывать лишь при определении осевой силы. Выделим на крыле элементарную площадку (рис. 4. 13) Рис. 4. 13

При малой кривизне верхней и нижней поверхностей крыла реальное распределение давления по ним можно заменить распределением давлений на плоскости х0 z. Тогда для элементарной нормальной силы d. Y, действующей на площадку d. S, имеем , а для момента от этой силы соответственно. Здесь х – координата площадки d. S. Интегрируя по площади крыла, для нормальной силы и момента тангажа получим Выражая давления рн и рв через коэффициенты давления, для коэффициента нормальной силы и момента тангажа и в соответствии с 4. 2 имеем (4. 5)

В дальнейшем будем пользоваться понятием коэффициентов нормальной силы и момента тангажа сечения, понимая под ними аэродинамические характеристики элемента крыла длиной b′ (местная хорда сечения) и шириной. Учитывая, что в этом случае интегрирование по площади, равной b′dz из формул (4. 5) получим (4. 6) Перейдем теперь к рассмотрению продольной силы. Эта сила обусловлена действием как касательных сил трения, так и нормальных сил давления или в безразмерном виде через коэффициенты сил (4. 7) Если – коэффициент трения пластины, а Sпов – площадь поверхности крыла, то

В силу малой относительной толщины крыла поэтому (4. 8) Определим коэффициент давления. В сечении крыла, нормальном к плоскости х0 z, выделим площадку (рис. 4. 14) Рис. 4. 14. К определению коэффициента давления Интегрируя по площади миделевого сечения Sм (наибольшей лобовой площади в плоскости у0 z) получим а безразмерный коэффициент будет (4. 9)

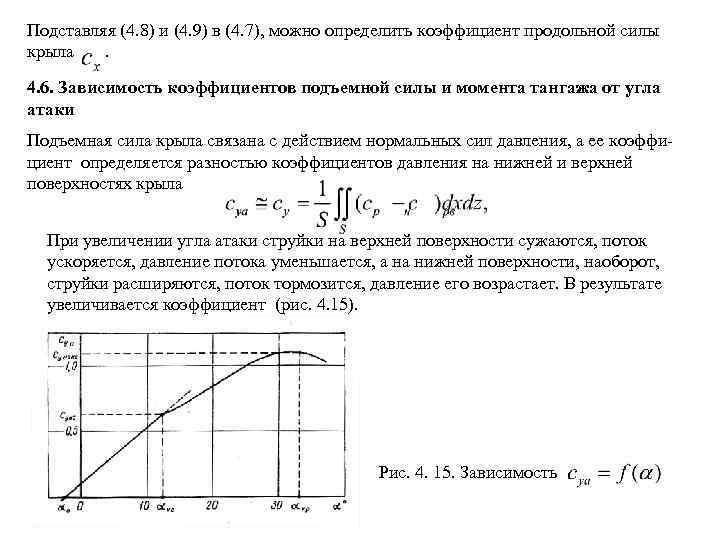Подставляя (4. 8) и (4. 9) в (4. 7), можно определить коэффициент продольной силы крыла. 4. 6. Зависимость коэффициентов подъемной силы и момента тангажа от угла атаки Подъемная сила крыла связана с действием нормальных сил давления, а ее коэффи циент определяется разностью коэффициентов давления на нижней и верхней поверхностях крыла При увеличении угла атаки струйки на верхней поверхности сужаются, поток ускоряется, давление потока уменьшается, а на нижней поверхности, наоборот, струйки расширяются, поток тормозится, давление его возрастает. В результате увеличивается коэффициент (рис. 4. 15). Рис. 4. 15. Зависимость

Исследования показывают, что при малых углах атаки коэффициент линейно зависит от угла. Это соответствует безотрывному режиму обтекания крыла. Объяснить это можно следующим образом. При плавном обтекании крыла поток поворачивает на угол , при этом изменение количества движения пропорционально или при малых углах атаки. Следовательно, импульс сил (в данном случае нормаль ных) прямо пропорционален углу атаки. С увеличением угла атаки крыла увеличивается разрежение на его верхней поверх ности и растёт положительный градиент давления др/дх в кормовой части (см. рис. 4. 12, б). При некотором угле атаки на крыле (например, вблизи задней кромки) возникает местный отрыв потока и линейная зависимость нарушается (угол и коэффициент соответствуют началу срыва). При дальнейшем увеличении угла атаки коэффициент растет до некоторого максимального значения , со ответствующего критическому углу атаки ( ). Начиная с дальнейшее увеличение угла атаки сопровождается падением коэффициента , так как срыв быстро распространяется на все крыло или большую его часть. При отрицательных углах атаки зависимость качественно такая же, как и при > 0, но при этом < 0. Если профиль симметричный и крыло незакрученное, то зависимость проходит через начало координат. В общем случае (рис. 4. 15) эта кривая смещена относительно начала координат, а угол , при котором = 0, называется углом нулевой подъем ной силы.

На линейном участке зависимости имеем (4. 10) Для незакрученного крыла с симметричным профилем = 0, (4. 11) Производная зависит от формы крыла в плане и критериев подобия. На линей ном участке кривой производная не зависит от угла атаки. Как следует из формулы (4. 5) коэффициент момента тангажа определяется не только разностью коэффициентов давления на верхней и нижней поверхностях крыла, но и законом распределения этой разности по площади крыла S и положением оси приве дения. При малых углах атаки коэффициент линейно зависит от угла атаки, а при больших углах атаки эта линейность нарушается вследствие влияния срыва потока (рис. 4. 16). Поскольку при возникновении срыва изменяется не только величина аэродинамичес ких нагрузок, но и характер их распределения по площади крыла, то нелинейная зависимость может быть более сложной, чем.

Рис. 4. 16. Зависимости крыла Поскольку при возникновении срыва изменяется не только величина аэродинамичес ких нагрузок, но и характер их распределения по площади крыла, то нелинейная зави симость может быть более сложной, чем. На линейном участке

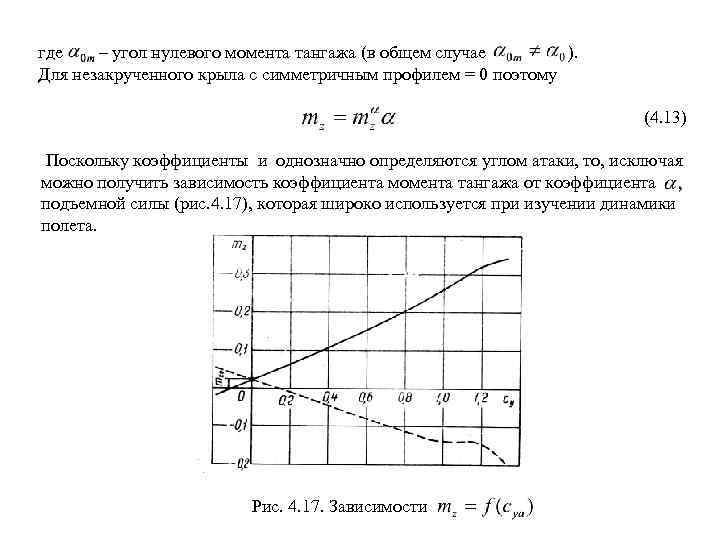где – угол нулевого момента тангажа (в общем случае ). Для незакрученного крыла с симметричным профилем = 0 поэтому (4. 13) Поскольку коэффициенты и однозначно определяются углом атаки, то, исключая можно получить зависимость коэффициента момента тангажа от коэффициента подъемной силы (рис. 4. 17), которая широко используется при изучении динамики полета. Рис. 4. 17. Зависимости

Характер зависимости аналогичен характеру зависимости при малых значе ниях зависимость линейна. Значение коэффициента момента при =0 обозначим. Тогда при малых значениях (4. 14) Производные и зависят от формы крыла, критериев подобия и положения оси приведения. Для различного положения этой оси зависимости и показаны на рис. 4. 16 и 4. 17. Коэффициент крыла связан с несимметричностью профиля и закрученностью крыла. В этом случае при некотором угле атаки ( ) распределение аэродинами ческой нагрузки в сечении может иметь вид, показанный на рис. 4. 18. В передней части подъемная сила направлена вниз, а в кормовой – такая же по величине подъемная сила направлена вверх. Рис. 4. 18. Распределение аэродинамической нагрузки несимметричного профиля

4. 7. Центр давления и аэродинамический фокус крыла Центром давления (ц. д) называется точка на продольной оси крыла (ЛА), через кото рую проходит линия действия равнодействующей аэродинамических сил. Найдем положение центра давления в связанной с крылом системе координат. Разложим равнодействующую силу R на две составляющие: X и Y (рис. 4. 19). Рис. 4. 19. Определение центра давления Момент тангажа относительно оси Oz будет или Отсюда При малых углах атаки , поэтому (4. 15)

Аэродинамическим фокусом (по углу атаки) называется точка на продольной оси крыла (ЛА), в которой приложено приращение подъемной силы, вызванное малым изменением угла атаки. Иными словами, момент тангажа относительно оси, проходящей через фокус остается постоянным при малых изменениях угла атаки. Обозначим координату фокуса , а ее безразмерную величину , Пусть известен момент относительно оси приведения. Найдем момент относительно оси, проходящей через фокус (рис. 4. 20): Рис. 4. 20. К понятию аэродинамического фокуса

или в безразмерном виде (4. 16) Поскольку по определению , то Дифференцируя (4. 16) по углу атаки , получим откуда (4. 17) Учитывая, что и сравнивая (4. 14) и (4. 16), находим (4. 18) Установим связь между координатами центра давления и фокуса. Подставив в (4. 15) значение из (4. 16), получим (4. 19) В общем случае фокус крыла не совпадает с центром давления Для незакрученного крыла с симметричным профилем =0 и Построим на одном графике зависимости , , , (рис. 4. 21).

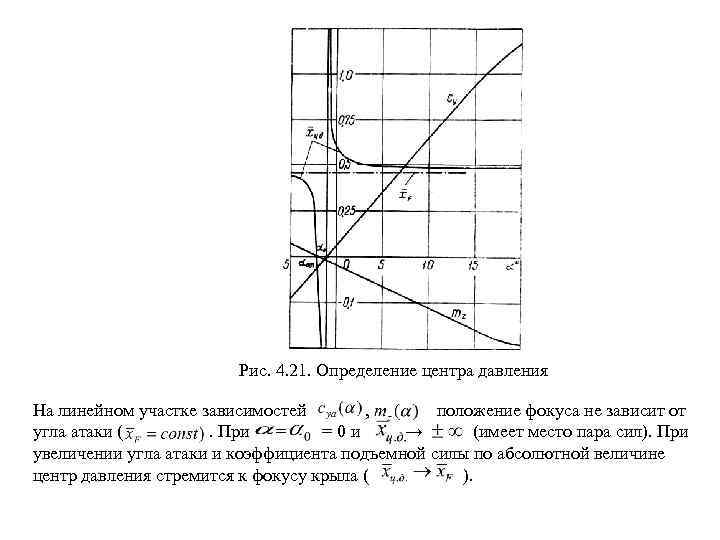Рис. 4. 21. Определение центра давления На линейном участке зависимостей , положение фокуса не зависит от угла атаки (. При = =0 и → (имеет место пара сил). При увеличении угла атаки и коэффициента подъемной силы по абсолютной величине центр давления стремится к фокусу крыла ( ).

ЛЕКЦИЯ 3 4. 8. Сопротивление крыла и его составляющие Рассмотрим обтекание крыла потоком реального газа под углом атаки. На крыло действует нормальная сила Y и осевая сила X. Им соответствуют коэффициенты и Найдем коэффициент лобового сопротивления Пусть = 0. Тогда и = 0. Обозначим через коэффициент сопротивления при. Так как это имеет место при малых углах атаки ( = 0), то в этом случае При отсутствии подъемной силы сопротивление создается силами трения и силами давления (4. 20) Если ( ), то из за разрежения потока на носке крыла при его обтекании возникает подсасывающая сила Т, направленная вдоль хорды вперед (рис. 4. 22).

Рис. 4. 22. Возникновение подсасывающей силы Введем безразмерный коэффициент этой силы фициента лобового сопротивления в этом случае имеем При малых углах атаки будем полагать , , > 0 для коэф Тогда получим Рассмотрим плоское незакрученное крыло с симметричным профилем, у которого , а (на линейном участке зависимости коэффициента подъемной силы от угла атаки). С учетом этого можем записать

С увеличением угла атаки, как показывают исследования, коэффициент увели чивается пропорционально. Следовательно, на линейном участке зависимости слагаемое не зависит от угла атаки. Обозначим (4. 21) Тогда (4. 22) Первое слагаемое ( ) в (4. 22) характеризует лобовое сопротивление при отсутствии подъемной силы и называется коэффициентом лобового сопротивления при нулевой подъемной силе. Второе слагаемое ( ) характеризует сопротивление, обус ловленное подъемной силой, и называется коэффициентом индуктивного сопротивления. Чем больше подъемная сила, тем больше это сопротивление. С увеличением угла атаки сопротивление крыла возрастает (рис. 4. 23).

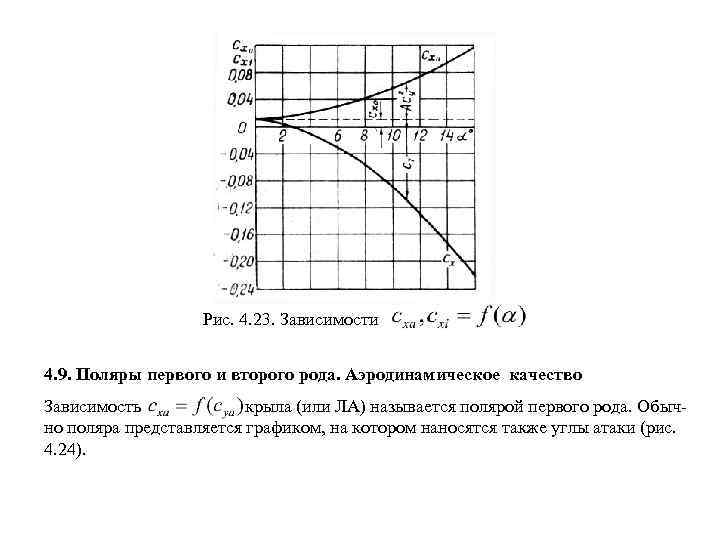Рис. 4. 23. Зависимости 4. 9. Поляры первого и второго рода. Аэродинамическое качество Зависимость крыла (или ЛА) называется полярой первого рода. Обыч но поляра представляется графиком, на котором наносятся также углы атаки (рис. 4. 24).

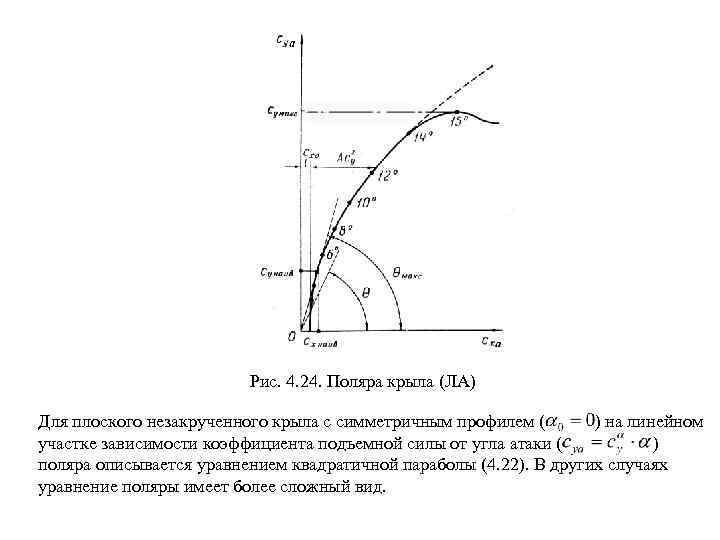Рис. 4. 24. Поляра крыла (ЛА) Для плоского незакрученного крыла с симметричным профилем ( ) на линейном участке зависимости коэффициента подъемной силы от угла атаки ( ) поляра описывается уравнением квадратичной параболы (4. 22). В других случаях уравнение поляры имеет более сложный вид.

В общем случае ( ) на линейном участке зависимость описывается уравнением (4. 10). С учетом этого для коэффициента сопротивления можем записать Окончательно имеем следующее выражение для несимметричной поляры: (4. 23) где коэффициент А определяется формулой (4. 21), а коэффициент А 1 =. При нелинейной зависимости уравнение поляры имеет еще более сложный вид. Рассмотрим поляру крыла (см. рис. 4. 24). При угле атаки, равном критическому, коэффициент подъемной силы достигает своего максимального значения и при дальнейшем увеличении угла атаки падает, а коэффициент сопротивления интен сивно растет, что объясняется срывом потока с крыла. При решении некоторых задач динамики полета требуется знание сил в связанной с крылом (ЛА) системе координат. Зависимость коэффициента продольной силы от коэффициента нормальной силы , т. е. зависимость называется полярой второго рода (рис. 4. 25).

Рис. 4. 25. Поляра второго рода описывается зависимостью (4. 24) При плавном обтекании крыла с увеличением угла атаки возрастает (подсасывающая сила (коэффициент растет), при этом коэффициент уменьшается и может стать отрицательным (появляется тянущая сила в плоскости крыла). Однако сопротивление крыла при этом всегда положительно ( > 0, рис. 4. 24). При возникновении срыва на крыле разрежение в его носовой части резко падает и при дальнейшем увеличении угла атаки коэффициент возрастает.

В аэродинамике крыла и летательного аппарата при оценке их аэродинамического совершенства важнейшее значение имеет качество – отношение коэффициента подъемной силы к коэффициенту лобового сопротивления. (4. 25) Если коэффициенты и отложены на графике в одном масштабе, то для определения качества по поляре 1 го рода достаточно провести луч из начала координат в соот ветствующую точку поляры, тогда (см. рис. 4. 24). Нетрудно видеть, что аэродинамическое качество зависит от угла атаки. С увеличением угла атаки аэроди намическое качество вначале возрастает, так как растет коэффициент , а коэффиц ент изменяется слабо, достигает максимального значения , а затем падает вследствие интенсивного роста лобового сопротивления (рис. 4. 26). Для нахождения по поляре необходимо к ней из начала координат провести касательную (см. рис. 4. 24), тогда. Угол атаки, коэффициенты и , при которых реализуется , называют наивыгоднейшими.

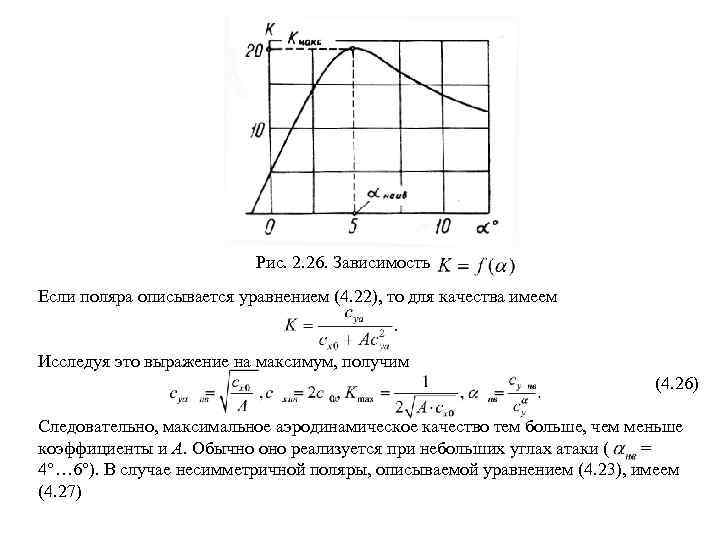Рис. 2. 26. Зависимость Если поляра описывается уравнением (4. 22), то для качества имеем Исследуя это выражение на максимум, получим (4. 26) Следовательно, максимальное аэродинамическое качество тем больше, чем меньше коэффициенты и А. Обычно оно реализуется при небольших углах атаки ( = 4 … 6 ). В случае несимметричной поляры, описываемой уравнением (4. 23), имеем (4. 27)

(4. 27) 4 10. Влияние числа Рейнольдса на аэродинамические характеристики крыла Как показывают исследования, число Рейнольдса, характеризующее влияние вязкости воздуха, на коэффициенты , и положение фокуса сказывается очень слабо, но оказывает существенное влияние на коэффициент лобового сопротивления, критичес кий угол атаки и коэффициент. Число Re влияет на структуру и характеристики пограничного слоя на крыле. При ма лых числах Re точка перехода ламинарного пограничного слоя в турбулентный сдви нута назад, большая часть пограничного слоя является ламинарной. Поскольку лами нарный слой менее устойчив к отрыву потока, то отрыв происходит при меньших положительных градиентах давления (на меньших углах атаки, при меньших значени ях коэффициента ). При увеличении числа Re точка перехода ламинарного пограничного слоя в турбулентный смещается вперед (координата уменьшается), протяженность турбулентного участка возрастает. Так как турбулентный пограничный слои более устойчив к отрыву потока, то отрыв потока происходит при больших поло жительных градиентах давления (на больших углах атаки при больших значениях коэффициентов ). В результате при увеличении числа Re величины и возрастают (рис. 4. 27).

Рис. 4. 27. Влияние числа Re на величину Однако их рост с увеличением числа Re не может быть беспредельным. Дело в том, что при некотором значении числа Re точка перехода смещается на переднюю кромку ( = 0), весь пограничный слой становится турбулентным. Дальнейшее уве личение числа Re не влияет на структуру пограничного слоя и рост и прекращается (наступает автомодельный режим).

Рассмотрим влияние числа Re на лобовое сопротивление. При безотрывном обтекании, когда коэффициент сопротивления описывается уравнением поляры (4. 22), лобовое сопротивление, обусловленное подъемной силой и характеризуемое величиной , от числа Re практически не зависит. От числа Re сильно зависит коэффициент , на малых скоростях в основном определяемый для крыла силами трения, так как в этом случае. Поэтому для определения коэффициента крыла при малых дозвуковых скоростях используется формула (4. 28) где – коэффициент одностороннего трения пластины. Известно, что коэффициент одностороннего трения пластины определяется числом Re и характером пограничного слоя (положением точки перехода ламинарного пограничного слоя в турбулентный безразмерной координатой ). Величина поправочного коэффициента (рис. 4. 28) зависит от относительной толщины профиля и положения точки перехода ламинарного пограничного слоя в турбулентный (координаты ).

Рис. 4. 28. Зависимость = ( , ) Как видно из рис. 3. 11 и 4. 28, влияние числа Re на коэффициент сказывается двояким образом. С одной стороны, увеличение числа Re при = const приводит к уменьшению величины коэффициента , с другой – при увеличении числа Re точка перехода смещается вперед, пограничный слой становится более турбулентным, координата уменьшается, а коэффициенты и возрастают. Исследования показывают, что итоговое влияние числа Re обычно является положительным – коэффициент крыла при увеличении числа Re несколько уменьшается (рис. 4. 29).

Рис. 4. 29. Влияние числа Re на коэффициент При возникновении срыва потока сопротивление крыла резко возрастает вследствие падения разрежения на верхней поверхности и уменьшения (или полного исчезнове ния) подсасывающей силы. Поэтому увеличение числа Re и затягивание срыва потока на большие углы атаки способствуют уменьшению коэффициента лобового сопротив ления (см. рис. 4. 29).

4. 11. Особенности обтекания стреловидного крыла Применение стреловидных крыльев (см. рис. 4. 2, в) связано с использованием эффекта скольжения. Рассмотрим скользящее крыло, т. е. крыло бесконечного размаха, у кото рого передняя кромка не перпендикулярна скорости набегающего потока, а скошена на угол скольжения β (рис. 4. 30). Рис. 4. 30. Скользящее в потоке крыло бесконечного размаха Разложим вектор скорости набегающего потока , на две составляющие: нормаль ную к передней кромке и тангенциальную. Очевидно, что (4. 29)

Тангенциальная составляющая никакого влияния на картину распределения давления на крыле бесконечного размаха не оказывает, поскольку движение газа вдоль размаха этого крыла не приводит к деформации струй. Проанализируем поведение струек жидкости на поверхности скользящего крыла. Поскольку при движении жидкости вдоль размаха скользящего крыла деформаций струек не происходит, то можно считать, что во всех точках его поверхности касательные составляющие скорости одинаковы, а направление линий тока опреде ляется изменением нормальной составляющей. Рассмотрим изменение скорости потока в сечении скользящего крыла (см. рис. 4. 30). По мере приближения к передней кромке поток тормозится, нормальная скорость уменьшается и поток разворачивается вправо. Далее при обтекании сечения крыла поток разгоняется, нормальная скорость возрастает и достигает максимальной величины в точке наибольшей толщины, а струйки разворачиваются влево. При приближении к задней кромке поток опять тормозится, скорость уменьшается, а струйки опять разворачиваются вправо, к исходному невозмущенному направлению. В результате линии тока в сечении скользящего крыла имеют вид, изображенный на рис. 4. 30. Сравним два крыла, совмещенных на рис. 4. 31: скользящее, обтекаемое потоком со скоростью под углом атаки , и нескользящее, обтекаемое потоком со скоростью под углом атаки .

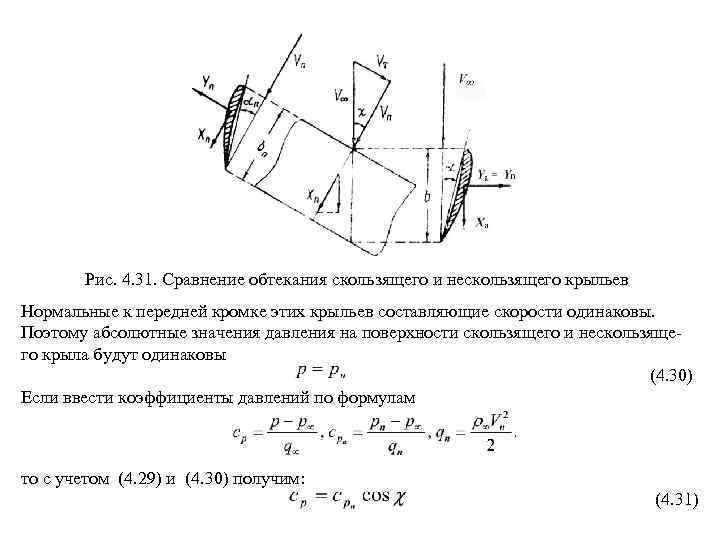Рис. 4. 31. Сравнение обтекания скользящего и нескользящего крыльев Нормальные к передней кромке этих крыльев составляющие скорости одинаковы. Поэтому абсолютные значения давления на поверхности скользящего и нескользяще го крыла будут одинаковы (4. 30) Если ввести коэффициенты давлений по формулам то с учетом (4. 29) и (4. 30) получим: (4. 31)

Следует заметить, что углы атаки скользящего и нескользящего крыльев неодина ковы. Установим связь между углами атаки скользящего ( ) и нескользящего ( n) крыльев. У обоих крыльев передняя кромка над задней имеет одинаковое превыше ние h. Но скользящее крыло имеет хорду b, а нескользящее. Из рис. 4. 31 имеем Отсюда или при малых углах атаки (4. 32) Выделим на нескользящем крыле элемент с площадью S. Пусть на него действует подъемная сила. В силу (4. 30) такая же подъемная сила будет действовать на выделенный элемент и при скольжении, т. е. . Учитывая, что получим (4. 33)

При линейной зависимости коэффициентов подъемной силы от угла атаки (4. 34) при этом С учетом (4. 32) и (4. 34) из (4. 33) имеем (4. 35) Таким образом, скользящее крыло имеет меньшие несущие свойства, чем нескользя щее. Рассмотрим сопротивление скользящего крыла. Как было показано выше, коэффици ент сопротивления трения определяется числом Re и состоянием пограничного слоя (с увеличением числа Re коэффициент обычно уменьшается). При скольжении крыла увеличиваются скорость ( ) и хорда крыла, а, следовательно, и число Re. Поэтому коэффициент трения несколько уменьшается. Однако основное влияние скольжение оказывает на сопротивление, обусловленное нормальными силами давления. Действительно, скольжение не изменяет этих сил, а следовательно, и. Из рис. 4. 31 следует, что (4. 36)

Учитывая, что из (4. 36) имеем (4. 37) Следовательно, скольжение сильно уменьшает коэффициент сопротивления сил давления. Это объясняется тем, что при наличии скольжения уменьшаются относи тельная толщина крыла и его кривизна. Из простых геометрических соображений следует, что (4. 38) Анализ показывает, что в тех случаях, когда сопротивление крыла определяется в основном силами трения (например, на малых дозвуковых скоростях), скольжение уменьшает аэродинамическое качество (вследствие падения несущих свойств). Наоборот, если более значительна роль сил давления в создании лобового сопротивле ния, то скольжение позволяет увеличить аэродинамическое качество (вследствие более интенсивного уменьшения сопротивления).

4. 16. Влияние формы крыла на распределенные аэродинамические характеристики Рассмотрим, как влияет форма крыла в плане на распределение аэродинамической нагрузки по хорде и размаху крыла. У крыла бесконечного размаха во всех его сече ниях условия обтекания и картина распределения давления одинаковы, поэтому коэф фициент подъемной силы сечений по размаху не изменяется (рис. 4. 32). Рис. 4. 32. Распределение давления вдоль крыльев различного удлинения

У крыла конечного размаха вследствие концевых перетеканий давления на нижней и верхней сторонах стремятся выровняться, особенно в концевых сечениях. Это приво дит к уменьшению аэродинамической нагрузки. В результате наибольшее значение имеет в корневом сечении; приближении к концам крыла коэффициент уменьшается, а непосредственно на концах – обращается в нуль. Это уменьшение тем значительнее, чем меньше удлинение крыла (см. рис. 4. 32). Эта объясняется тем, что на крыльях большого удлинения роль концевых перетеканий относительно невелика. При уменьшении удлинения возрастает длина концевой хорды, через которую проис ходит перетекание воздуха с нижней поверхности на верхнюю, а влияние этого пере текания распространяется на относительно большую часть площади крыла. При этом несколько изменяется характер распределения нагрузки и по хорде крыла (рис. 4. 33). Рис. 4. 33. Распределение коэффициента давления сечений крыльев различного удлинения

Существенно уменьшается нагрузка в кормовой части сечений и подъемная сила все больше сосредоточивается вблизи передней кромки, где происходит основная дефор мация струек воздуха при обтекании крыла, поставленного под углом атаки. Рассмотрим влияние стреловидности крыла на его распределенные характеристики. Стреловидное крыло (рис. 4. 34) отличается от рассмотренного выше скользящего конечностью размаха и наличием излома на стыке двух полукрыльев. Рис. 4. 34. Обтекание стреловидного крыла

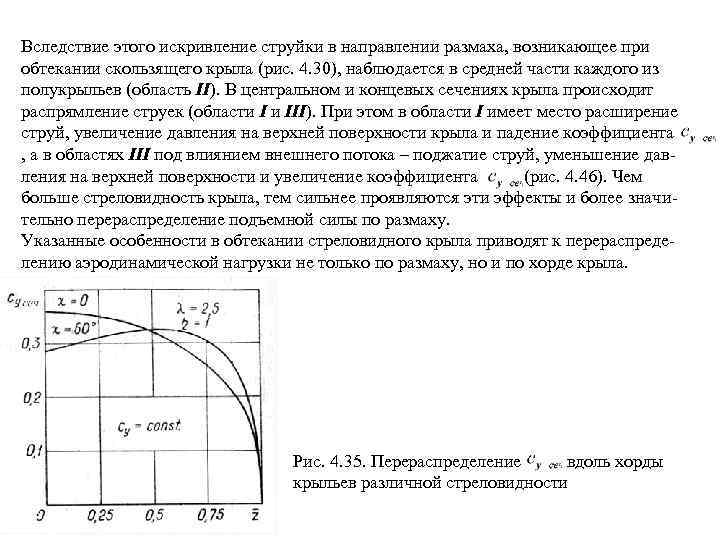Вследствие этого искривление струйки в направлении размаха, возникающее при обтекании скользящего крыла (рис. 4. 30), наблюдается в средней части каждого из полукрыльев (область II). В центральном и концевых сечениях крыла происходит распрямление струек (области I и III). При этом в области I имеет место расширение струй, увеличение давления на верхней поверхности крыла и падение коэффициента , а в областях III под влиянием внешнего потока – поджатие струй, уменьшение дав ления на верхней поверхности и увеличение коэффициента (рис. 4. 46). Чем больше стреловидность крыла, тем сильнее проявляются эти эффекты и более значи тельно перераспределение подъемной силы по размаху. Указанные особенности в обтекании стреловидного крыла приводят к перераспреде лению аэродинамической нагрузки не только по размаху, но и по хорде крыла. Рис. 4. 35. Перераспределение вдоль хорды крыльев различной стреловидности

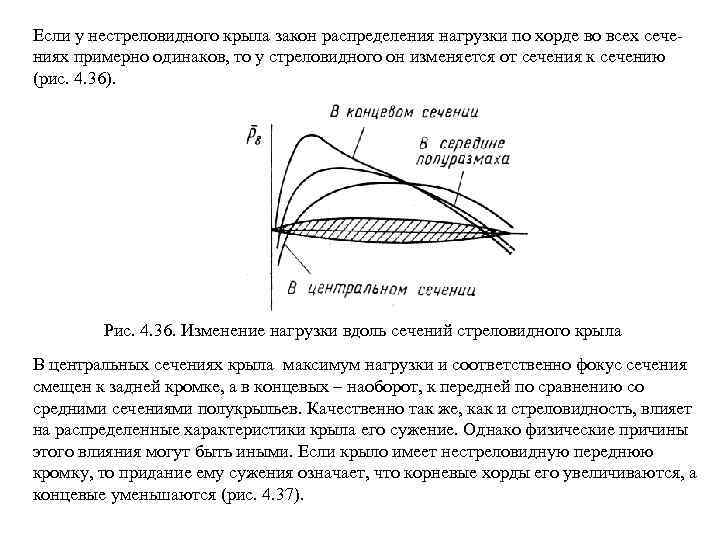Если у нестреловидного крыла закон распределения нагрузки по хорде во всех сече ниях примерно одинаков, то у стреловидного он изменяется от сечения к сечению (рис. 4. 36). Рис. 4. 36. Изменение нагрузки вдоль сечений стреловидного крыла В центральных сечениях крыла максимум нагрузки и соответственно фокус сечения смещен к задней кромке, а в концевых – наоборот, к передней по сравнению со средними сечениями полукрыльев. Качественно так же, как и стреловидность, влияет на распределенные характеристики крыла его сужение. Однако физические причины этого влияния могут быть иными. Если крыло имеет нестреловидную переднюю кромку, то придание ему сужения означает, что корневые хорды его увеличиваются, а концевые уменьшаются (рис. 4. 37).

Рис. 4. 37. Изменение размера концевой хорды относительно корневой стреловидного крыла При этом по картине обтекания корневые сечения приближаются к сечениям крыла малого удлинения и аэродинамическая нагрузка в них уменьшается по сравнению с исходным крылом без сужения, а концевые – к сечениям крыла большого удлинения и нагрузка в них возрастает. В результате коэффициент по размаху крыла с суже нием изменяется так, как показано на рис. 4. 38.

Рис. 4. 38. Распределение вдоль крыла различного сужения Если крыло с сужением η > 1 имеет еще и стреловидную переднюю кромку, то на характер изменения по размаху оказывает влияние и стреловидность. В частности, у треугольных крыльев ( ) коэффициент в концевых сечениях теоретически стремится к бесконечности.

Крыло сложной формы в плане (переменной по размаху или изменяемой в полете стреловидности) сочетает в себе особенности крыла малого удлинения большой стреловидности и большого сужения (наплыв) и нестреловидного крыла большого удлинения (консоль). Распределение коэффициента такого крыла по размаху показано на рис. 4. 39. Рис. 4. 39. Распределение коэффициента по размаху крыла сложной формы в плане

Как видно, максимальное значение у крыла сложной формы в плане обычно достигается в месте стыка наплыва с консолью. Крылья многих современных самоле тов имеют геометрическую крутку. При повороте концевых сечений таких крыльев на уменьшение углов атаки перераспределение нагрузки по размаху происходит таким образом, что в концевых сечениях коэффициент уменьшается, а в корневых – возрастает. Для сравнения законов распределения по размаху крыльев различной формы удобно их рассматривать при одинаковом значении коэффициента суа всего крыла. На рис. 4. 40 показаны законы изменения отношений для прямоугольного, стреловидного ( χ = 60°, η = 1) и треугольного (χ = 60°, η = ∞) крыльев одинакового удлинения ( λ = 2. 5). Рис. 4. 40. Законы изменения отношений различных крыльев для

4. 17. Влияние геометрических параметров крыла на его суммарные характеристики Рассмотрим влияние удлинения, стреловидности, сужения и других геометрических характеристик крыла на коэффициенты подъемной силы, лобового сопротивления и координату фокуса. Несущие свойства и положение фокуса крыльев существенно зависят от их удлинения. Крыло бесконечного размаха (λ = ∞) имеет максимальное значение коэффициента равное 2π, а фокус у этого крыла расположен да расстоянии одной четверти хорды от ее носка ( =1/4). При уменьшении удлинения возрастает влияние перетекания воздуха через боковые кромки, при этом несущие свойства крыла уменьшаются тем сильнее, чем меньше удлинение крыла (рис. 4. 41), а фокус смещается вперед (рис. 4. 42). Рис. 4. 41. Зависимость

Рис. 4. 42. Зависимость Для крыльев весьма малых удлинений (λ → 0) теория дает следующее решение: (4. 39) при этом 0. Смещение фокуса вперед при уменьшении удлинения объясняется тем, что в этом случае крыло все больше удлиняется по потоку, увеличивая область перетекания потока и выравнивания давлений на нижней и верхней поверхностях крыла. Поскольку основная деформация струй (поворот потока) при обтекании крыла осуществляется в носовой части крыла, то нагрузка все больше сосредоточивается вблизи передней кромки (см. рис. 4. 33).

Рассмотрим влияние стреловидности на несущие свойства и положение фокуса крыла. Как было показано выше (см. рис. 4. 34), эффект скольжения наиболее сильно прояв ляется в средней части полукрыльев, где при увеличении угла стреловидности подъем ная сила уменьшается. Что касается корневого и концевых сечений, то уменьшение несущих свойств на стыке в определенной степени компенсируется их подрастанием на торцах. Поэтому характер влияния угла стреловидности на производную зависит от удлинения – чем больше удлинение крыла, тем больше роль средней части полукрыль ев, тем сильнее уменьшается производная при увеличении стреловидности и наоборот (рис. 4. 42). Поскольку при увеличении стреловидности нагрузка в корневых сечениях уменьшается, а в концевых, сдвинутых назад, – возрастает, то фокус крыла при этом смещается назад (рис. 4. 43). Рис. 4. 42. Зависимости Рис. 4. 43. Зависимости

При изменении сужения η происходит перераспределение нагрузки по размаху, поэтому производная изменяется незначительно (рис. 4. 44), а фокус при увеличении несколько смещается вперед (рис. 4. 45). Относительная толщина крыльев сравнительно слабо влияет на аэродинамические характеристики при малых дозвуковых скоростях. Рис. 4. 44. Зависимости Рис. 4. 45. Зависимости Кривизна профиля и крутка крыла оказывают влияние на и крыла бесконечного размаха теория дает следующие формулы: . В частности, для (4. 40) Рассмотрим влияние геометрических параметров крыла на коэффициент лобового сопротивления. Исследования показывают, что форма крыла при малых дозвуковых скоростях слабо влияет на коэффициент , но оказывает существенное влияние на коэффициент А. Коэффициент А определяется по формуле (4. 21) и зависит от несущих свойств крыла ( ) и степени реализации подсасывающей силы.

В случае эллиптического закона распределения аэродинамической нагрузки по размаху и полной реализации подсасывающей силы теория дает (4. 41) В общем случае обычно полагают (4. 42) где – некоторое эффективное удлинение крыла (рис. 4. 46). Рис. 4. 46. Зависимости

Исследования показывают, что с уменьшением удлинения и увеличением стреловид ности эффективное удлинение уменьшается (см. рис. 4. 46), коэффициент А и сопро тивление, обусловленное подъемной силой, возрастают (рис. 4. 47 и 4. 48). Рис. 4. 47. Поляры крыльев различного удлинения Рис. 4. 48. Поляры крыльев различной стреловидности Наличие сужения приводит к некоторому уменьшению подсасывающей силы и возрастанию лобового сопротивления. Если подсасывающая сила не реализуется ( = 0), что имеет место в случае острой передней кромки, то (4. 43) Сопротивление крыла при этом возрастает (рис. 4. 49).

Рис. 4. 49. Поляры крыльев с закругленной и острой передней кромками На практике подсасывающая сила может реализоваться лишь частично, поэтому (4. 43) Существенное влияние на поляру крыла оказывает кривизна профиля и крутка.

Применяя крутку крыла, можно оптимальным образом распределить нагрузку по раз маху, увеличить подсасывающую силу, уменьшить сопротивление, обусловленное подъемной силой, особенно на больших углах атаки (при больших ) и существенно повысить максимальное аэродинамическое качество (рис. 4. 50) Рис. 4. 50. Поляры крыльев с круткой и без крутки

5. 1. Влияние сжимаемости на обтекание крыла В гл. IV была рассмотрена задача обтекания крыла несжимаемым потоком газа, когда числа М предполагались весьма малыми, а плотность постоянной. Однако, как показывает опыт, аэродинамические характеристики существенно зависят от числа М полета. Проанализируем эту зависимость. Рассмотрим струйку 1, обтекающую верх нюю поверхность профиля (рис. 5. 1). Рис. 5. 1. Струйка газа в сжимаемом потоке Обозначим параметры газа далеко впереди перед телом через , а в произ вольном сечении струйки – через. Запишем для этих сечений уравнение энергии (5. 1) Преобразуем это выражение к виду (5. 2)

Для случаев, представляющих в аэродинамике практический интерес, второй член в скобках меньше единицы и вследствие этого правая часть в (5. 2) может быть пред ставлена в виде сходящегося ряда (5. 3) Разложим выражение (5. 2) в ряд (5. 3). После ряда преобразований получим (5. 4) где (5. 5) Для коэффициента давления получим (5. 6) Если положить поправку на сжимаемость равной нулю выражении (5. 6) к коэффициенту давления в сжимаемом потоке. то придем в

Как следует из (5. 5), поправка всегда положительна (т. е. и при М > 1 и при М < 1). Известно, что в дозвуковом потоке в сужающейся струйке скорость возрастает, а в расширяющейся – падает. В сверхзвуковом же потоке, наоборот, скорость растет в расширяющейся струйке и падает в сужающейся. Из уравнения постоянства расхода следует, что в сжимаемом потоке падение плотности в струйке 1 (см. рис. 5. 1) ведет к дополнительному приросту скорости V. Там, где в дозвуковом потоке скорость V растет, там же она в сверхзвуковом потоке падает. Другими словами, как следует из (5. 5), если в дозвуковом потоке поправка на сжимаемость растет, то в сверхзвуковом потоке она падает. Рассмотрим струйку 1 (рис. 5. 1) в дозвуковом потоке газа. Нетрудно видеть, что скорости в струйке вначале, до самого узкого места в струйке, растут, а затем падают. Поправка на сжимаемость в (5. 6) вначале растет, а затем падает, оставаясь положительной. С увеличением числа М на профиле в самом узком его сечении еще при дозвуковом числе М набегающего потока местная скорость в струйке достигнет местной скорости звука (Vм = ам). А далее вниз по потоку образуется сверхзвуковая зона с замыкающим ее скачком уплотнения. В сверхзвуковой зоне вдоль оси Охa (рис. 5. 1) скорости V растут, растет и поправка на сжимаемость . За скачком уплотнения скорости вдоль оси Охa падают, падает и поправка на сжимае мость.

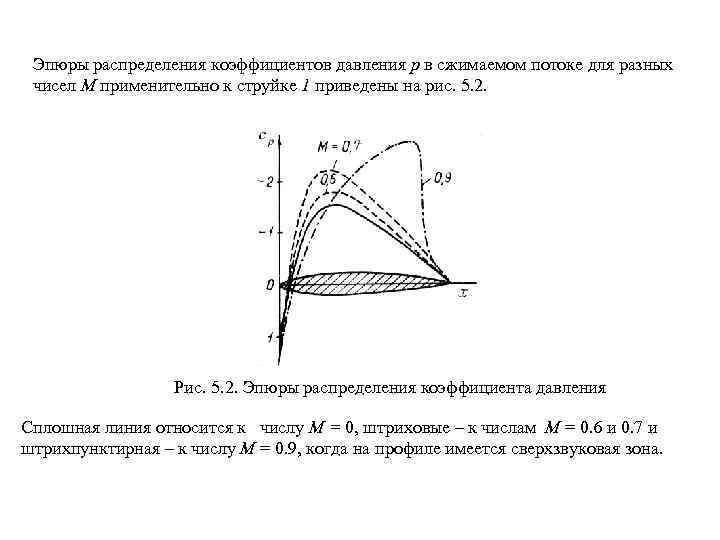Эпюры распределения коэффициентов давления р в сжимаемом потоке для разных чисел М применительно к струйке 1 приведены на рис. 5. 2. Рис. 5. 2. Эпюры распределения коэффициента давления Сплошная линия относится к числу М = 0, штриховые – к числам М = 0. 6 и 0. 7 и штрихпунктирная – к числу М = 0. 9, когда на профиле имеется сверхзвуковая зона.

Падение коэффициента давления при М = 0. 9 на переднем скате профиля объясняется тем, что возмущения вблизи тела, где скорость сверхзвуковая, не могут распростра няться вперед, против течения. Значительная часть профиля в сверхзвуковой зоне и за ней не участвует в создании разрежения на передней части профиля. Непосредственно вблизи передней кромки, вследствие торможения потока, как следует из выражения (5. 6), коэффициент давления положительный и больше единицы. Рассмотрим далее струйку 2 (см. рис. 5. 1), которая одним концом опирается на район критической точки профиля А, в которой скорость V = 0. Выражение (5. 6) в этом случае примет вид (5. 7) где В данном случае поправку на сжимаемость можно вычислить. Результаты расчета сведены в табл. 5. 1. Таблица 5. 1 М 0. 2 0. 4 0. 6 0. 8 1. 0 1. 2 1. 5 0. 01 0. 04 0. 09 0. 17 0. 27 0. 42 0. 70

Из табл. 5. 1 следует, что в критической точке А влияние сжимаемости воздуха становится практически ощутимым лишь при числах М, больших 0. 4 … 0. 5. 5. 2. Критическое число М и факторы, влияющие на него Число М невозмущенного потока, при котором у поверхности крыла впервые местная скорость становится равной местной скорости звука (Vм = aм), называется критическим числом М и обозначается М кр. Достижение Vм = aм происходит при неодинаковых числах М для разных тел. У тол стых крыльев струйки деформируются больше и это происходит раньше, у тонких – позже. Указанное равенство для современных крыльев раньше достигается также на верхних поверхностях. Поэтому проведем анализ влияния различных факторов на М кр, рассматривая верхнюю поверхность крыла. Влияние относительной толщины и кривизны профиля. При су = 0 весьма тонкий симметричный профиль ( > 0) струйки не деформирует, поэтому можно считать в этом случае М кр ≈ 1. С увеличением относительной толщины (или кривизны с выпуклостью вверх) струйки все больше деформируются. Местные числа М в них становятся больше числа М невозмущенного потока и М кр уменьшается (штриховая линия на рис. 5. 3),

Рис 5. 3. Зависимость М кр = f( ) При су > 0, например, при наличии угла атаки, у весьма тонкого профиля наблюдаются большие скорости при обтекании передней кромки. Теоретически при су > 0 они стремятся к бесконечности, а число М кр стремится к нулю. С увеличением относительной толщины профиля, при условии, что соответственно будет закруглен его носок, число М кр будет расти. При какой то относительной толщине влияние носка станет менее эффективным, чем деформация струйки на поверхности профиля, и М кр начнет уменьшаться (рис. 5. 3, сплошная линия). Изменение кривизны профиля сместит кривую вправо или влево.

Влияние формы крыла в плане. С уменьшением удлинения крыла вследствие выравнивания давления между нижней и верхней сторонами уменьшаются разрежения на верхней стороне. Уменьшение разрежения, согласно уравнению энергии, соответствует уменьшению скоростей в струйках и, следовательно, увеличению Мкр. На Мкр сильно влияет стреловидность крыла. Рассмотрим рис. 5. 4, на котором изобра жен участок скользящего крыла. Рис. 5. 4. Участок скользящего крыла

Поток набегает на крыло с числом М, Мп нормальная составляющая этого числа, а Мτ – тангенциальная (параллельная передней кромке). Так как при обтекании скользящего крыла тангенциальная составляющая скорости не изменяется, то, очевидно, что на Мкр влиять будет лишь поток, направленный по нормали к передней кромке. Но Мп = М cosχ, и местная скорость на крыле достигнет местной скорости звука, когда Мп = Мкр. Поэтому (5. 9) Формула (5. 9) определяет Мкр скользящего крыла. У скользящего крыла возможно Мкр > 1. Здесь не учитываются особенности, связанные с обтеканием реального стреловидного крыла, например, с сужением, обтеканием средних и концевых его частей. Поэтому для реального крыла обычно Мкр < 1. 5. 3. Линейная теория крыла в сжимаемом дозвуковом потоке Рассмотрим обтекание тонкого слабоизогнутого крыла конечного размаха, постав ленного под малым углом атаки в дозвуковом потоке, с учетом сжимаемости. Будем рассматривать числа М < Мкр. Задачу по определению аэродинамических характе ристик можно решать в линейной постановке.

Задача решается при выполнении условий плавного обтекания, на пелене, на бесконе чности и на задней кромке крыла. Однако в дозвуковом потоке в рассматриваемом стационарном случае задачу можно решить иным, более простым путем, основываясь на решениях, полученных в несжимаемом потоке. Действительно, рассмотрим уравнение для потенциала скорости в несжимаемом потоке. Заметим, что если в уравнении (1. 82) ввести новые независимые переменные, то оно сведется к уравнению (1. 39). (5. 10) Индекс «н» означает несжимаемый поток. Следовательно, зависимости (5. 10) связы вают между собой точки сжимаемого и несжимаемого потоков с равными значениями потенциала скоростей φ'. Трансформация потока приводит к следующим зависимос тям: для возмущенных параметров: (5. 11)

Воспользуемся далее выражением для возмущенного коэффициента давления, и с учетом (5. 11) получим (5. 12) Поделив левую и правую части (5. 12) на скоростной напор, получим связь для коэффициентов давления в сжимаемом и несжимаемом потоках (5. 13) Суммарные аэродинамические характеристики, зависящие от давления, будут иметь соответствующие связи (5. 14)

Трансформации подвергается не только поток, но и само крыло. Все координаты заданного (исходного) крыла нужно удлинить в направлении оси Оха в раз с сохранением местных углов атаки в соответствующих точках исходного и нового крыла. Это означает, что нужно рассматривать крыло с параметрами (5. 15) На рис. 5. 5 представлено заданное крыло в сжимаемом потоке и крыло, преобразо ванное для его расчета в несжимаемом потоке (показано штриховыми линиями). Задача по определению аэродинамических характе ристик в сжимаемом потоке решается следующим образом. Находятся по формулам (5. 15) параметры преобразованного крыла. Для него рассчитываются аэродинамические характеристики в несжимаемом потоке. Затем по формулам (5. 14) рассчитываются характеристики заданного крыла в сжимаемом потоке. Рис. 5. 5. Трансформация крыла

5. 4. Аэродинамические характеристики профиля приближении к скорости звука. Волновое сопротивление Сжимаемость воздуха существенно влияет на зависимости аэродинамических коэффициентов от числа М полета. Наиболее контрастно это влияние проявля ется для крыла бесконечного размаха (профиля), у которого отсутствуют перете кания воздуха с нижней поверхности на верхнюю. На рисунке показаны эпюры распределения давления на верхней и нижней поверхности профиля, обтекаю щегося потоком воздуха на больших дозвуковых скоростях (М = 0. 2 … 1. 0).

На следующем рисунке представлена зависимость производной , которая разбита на участки (а b), (b с) и т. д. Будем рассматривать ее совместно с рисунком эпюр давления. До числа Mкр (участок а b) коэффициент несколько возрастает, что связано с вли янием сжимаемости. Участок (b с) характеризуется наличием сверхзвуковой зоны и местного скачка уплотнения на верхней поверхности профиля. При увеличении числа М местный скачек на верхней стороне профиля смещается назад, увеличивая зону сверхзвуковых скоростей. В этой зоне разрежение резко возрастает, растет и производная. Точка «с» характерна тем, что на данном числе М сверхзвуковая зона и местный скачек уплотнения образуется и на нижней поверхности.

На участке (с d) разрежение возрастает снизу, производная падает. При даль нейшем увеличении числа М скачек на поверхности также смещается назад, при чем быстрее, чем на верхней. Точка «d» характерна тем, что скачек уплотнения на нижней поверхности достиг задней кромки профиля. На верхней же поверх ности этого не произошло. Последнее обстоятельство объясняется наличием уг ла атаки профиля, а именно, струйки у задней кромки снизу имеют меньшие се чения, чем сверху, сверхзвуковое течение в этом месте раньше наступит снизу. На участке (d – e) продолжает увеличиваться сверхзвуковая зона на верхней по верхности, коэффициент производной растет. Рассмотрим характер протекания зависимости профиля по числам М. Рис. 5. 8. Зависимость

Кривая разбита на участки (а b), (b с) и т. д. Будем рассматривать характер из менения кривой совместно с рисунком эпюр распределения избыточных давле ний (pв pн) по верхней и нижней образующим профиля для ряда обозначенных на рисунке участков. Некоторое уменьшение коэффициента сопротивления на участке (a – b), объясняется ростом числа Рейнольдса. Местные скорости на верхней поверхности профиля больше, чем на нижней поверхности и, следова тельно, на верхней поверхности раньше (на меньшей скорости полета) начнет сказываться влияние сжимаемости. Разрежения сверху профиля будут возрастать более интенсивно, чем снизу. По той же причине на верхней поверхности про филя (вследствие наличия больших скоростей на ней) равенство (V = а) будет достигнуто раньше (точка b). Участок (b с) характеризуется наличием сверхзву ковой зоны и местного скачка уплотнения на верхней поверхности профиля. При увеличении числа М местный скачок на верхней стороне профиля смещается на зад, увеличивая зону сверхзвуковых скоростей. Растет и значение. Точка (с) на рис. 1 характерна тем, что на данном числе М сверхзвуковая зона и местный ска чок уплотнения образуются и на нижней поверхности. При дальнейшем увеличе нии числа М скачок на нижней поверхности также смещается назад, причем бы стрее, чем на верхней поверхности. Точка d характерна тем, что скачок уплотне ния на нижней поверхности достиг задней кромки профиля. На верхней же по верхности этого не произошло.

Кривая разбита на участки (а b), (b с) и т. д. Будем рассматривать характер из менения кривой совместно с рисунком эпюр распределения избыточных давле ний (pв pн) по верхней и нижней образующим профиля для ряда обозначенных на рисунке участков. Некоторое уменьшение коэффициента сопротивления на участке (a – b), объясняется ростом числа Рейнольдса. Местные скорости на верхней поверхности профиля больше, чем на нижней поверхности и, следова тельно, на верхней поверхности раньше (на меньшей скорости полета) начнет сказываться влияние сжимаемости. Разрежения сверху профиля будут возрастать более интенсивно, чем снизу. По той же причине на верхней поверхности про филя (вследствие наличия больших скоростей на ней) равенство (V = а) будет достигнуто раньше (точка b). Участок (b с) характеризуется наличием сверхзву ковой зоны и местного скачка уплотнения на верхней поверхности профиля. При увеличении числа М местный скачок на верхней стороне профиля смещается на зад, увеличивая зону сверхзвуковых скоростей. Растет и значение. Точка (с) на рис. 1 характерна тем, что на данном числе М сверхзвуковая зона и местный скачок уплотнения образуются и на нижней поверхности. При дальнейшем уве личении числа М скачок на нижней поверхности также смещается назад, причем быстрее, чем на верхней поверхности. Точка d характерна тем, что скачок уплот нения на нижней поверхности достиг задней кромки профиля. На верхней же поверхности этого не произошло.

Последнее обстоятельство объясняется опять таки наличием утла атаки профиля, а именно, струйки у задней кромки снизу имеют меньшие сечения, чем вверху, сверхзвуковое течение в этом месте раньше наступит снизу. На участке (d – e) продолжает увеличиваться сверхзвуковая зона на верхней поверхности, коэффициент растет. На участке (а b) до Mкр коэффициент определяется в основном сопротивле нием трения, которое с увеличением числа М несколько уменьшается. Рассматривая эпюры распределения давления, приведенные на рис. 5. 6 (участки b – с, с d, d е), необходимо обратить внимание на то, что наибольшие разрежения как на нижней, так и на верхней стороне профиля смещены на его кормовую часть. Проектируя теперь силы давления на направление скорости набегающего потока, получаем силу (коэффициент на рис. 5. 3). Силу принято называть волновым сопротивлением, а коэффициент – коэффициентом волнового сопротивления. Волновое сопротивление может в несколько раз превосходить сопротивление трения. Существует выражение «звуковой барьер» , возникшее в то время, когда происходило освоение авиацией трансзвуковых скоростей, и намечались пути выхода на числа М полета больше единицы. Явления интенсивного изменения аэродинамических характеристик при M > Mкр получили название волнового кризиса. При наличии на крыле волнового сопротивления формулу для коэффициента будем в дальнейшем представлять в виде (5. 16)

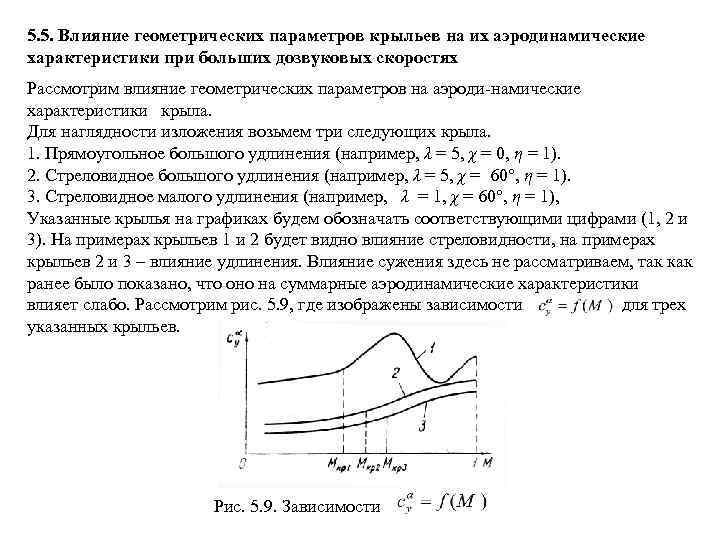5. 5. Влияние геометрических параметров крыльев на их аэродинамические характеристики при больших дозвуковых скоростях Рассмотрим влияние геометрических параметров на аэроди намические характеристики крыла. Для наглядности изложения возьмем три следующих крыла. 1. Прямоугольное большого удлинения (например, λ = 5, χ = 0, η = 1). 2. Стреловидное большого удлинения (например, λ = 5, χ = 60°, η = 1). 3. Стреловидное малого удлинения (например, λ = 1, χ = 60°, η = 1), Указанные крылья на графиках будем обозначать соответствующими цифрами (1, 2 и 3). На примерах крыльев 1 и 2 будет видно влияние стреловидности, на примерах крыльев 2 и 3 – влияние удлинения. Влияние сужения здесь не рассматриваем, так как ранее было показано, что оно на суммарные аэродинамические характеристики влияет слабо. Рассмотрим рис. 5. 9, где изображены зависимости для трех указанных крыльев. Рис. 5. 9. Зависимости

Прямоугольное крыло, вследствие большого удлинения, будет по характеру зависи мости напоминать крыло бесконечного удлинения (см. рис. 5. 7). Характер этих зависимостей для других крыльев практически одинаков и значительно отличается от крыла 1. Здесь, вследствие наличия стреловидности (крыло 2) и допол нительно к этому небольшого удлинения (крыло 3), производная меньше, причем на крыле 3 меньше, чем на крыле 2. Критическое число Mкр у крыла 2 больше, чем у крыла 1, а у крыла 3 больше, чем у крыла 2. На рис. 5. 10 приведены зависимости для трех рассматриваемых крыльев. Рис. 5. 10. Зависимости

Из рисунка видно, что сопротивление трения, которое является основным до Мкр , приблизительно одинаково у всех трех крыльев. Качественное различие начинается после Мкр1. При этом характер протекания зависимости для крыла 1, вследствие большого удлинения, такой же, как у профиля (см. рис. 5. 8). Придание крылу стреловидности, с одной стороны, увеличивает Мкр, а с другой – смягчает так называемый волновой кризис, т. е. кривая 2 не имеет такого большого максимума, кик у крыла 1, и максимум этот сдвинут в область сверхзвуковых чисел М. Влияние стреловидности на рассмотрено в гл. IV. Уменьшение удлинения стреловидного крыла приводит к усилению выравнивания давления между верхней и нижней поверхностями. Уменьшаются местные скорости в струйках. Число Мкр возрастает (Мкр 3 > Мкр 2). Волновой кризис проходит еще более «мягко» , чем для крыла 2. Максимум смещается еще больше в сторону сверхзвуковых чисел М. Рассмотрим для выбранных трех крыльев характер изменения коэффициента А по числам М. Из формулы (4. 21) следует, что зависимость А(М) будет определяться зависимостями (М). Зависимости А(М) приведены на рис. 5. 11. Рис. 5. 11. Зависимости А(М)

До числа Мкр коэффициент А остается приблизительно постоянным. С чисел М > Мкр образование сверхзвуковых зон на профиле приводит к резкому падению коэффици ента и, хотя производная продолжает расти, коэффициент А также растет. Падение коэффициента при М > Мкр вызвано образованием на крыле сверхзвуковых зон. Разрежение в сверхзвуковой зоне сверху крыла не влияет на его нижнюю поверхн ость. Перетекание потока через переднюю кромку уменьшается, уменьшается разрежение вблизи нее (см. рис. 5. 6). Увеличение стреловидности и уменьшение удлинения (крылья 2 и 3) приводят к уменьшению производной по сравнению с крылом 1, поэтому до Мкр коэффициенты А крыльев 2 и 3 больше, чем для крыла 1 (см. рис. 5. 11). Увеличение пространственности обтекания крыльев 2 и 3 по сравнению с крылом 1 приводит к сглаживанию эффектов, связанных с образованием сверхзвуковых зон на крыле. Поэтому рост коэффициента А при числах М > Мкр менее значителен, чем для крыла 1 (см. рис. 5. 11). Рассмотрим характер изменения максимального качества по числам М для трех рас сматриваемых крыльев. Из формулы (4. 26) следует, что характер зависимости от чис ла М определяется изменением по числам М характеристик и А, рассмотренных выше. Зависимости приведены на рис. 5. 12.

Рис. 5. 12. Зависимости Коэффициенты и А до чисел Мкр (Мкр 1, Мкр 2 и Мкр 3) практически не зависят от М (см. рис. 5. 10 и 5. 11). Затем после Мкр для крыла 1 резко уменьшается, а для крыльев 2 и 3 уменьшение менее значительно. Следовательно, стреловидные крылья и крылья малого удлинения при числах М > Мкр могут иметь значение большее, чем у прямоугольных крыльев. На рис. 5. 13 показан характер изменения безразмерной координаты фокуса для крыльев 1, 2 и 3. Видно значительное отличие в характере протекания кривых крыла 1 и крыльев 2 и 3.

Для пояснения данного обстоятельства рассмотрим вначале прямоугольное крыло и отметим на нем условно область, на которую значительно влияет выравнивание дав ления на боковых кромках крыла и захватывает в большей степени задние его скаты, чем передние. Рис. 5. 13. Зависимости Влияние сжимаемости увеличивает перепад давления между нижней и верхней поверхностями крыла. Одновременно увеличивается и выравнивание давления. Это приводит к смещению фокуса вперед. На крыльях 2 и 3 такого явления не происхо дит, вследствие более пространственной картины их обтекания.

При числах М > Мкр на верхней поверхности крыла образуются сверхзвуковые зоны и, следовательно, дополнительные разрежения. Эти разрежения образуются на задних скатах профиля (см. рис. 5. 6). Поэтому фокус смещается назад. Увеличение стреловидности крыла смещает фокус назад, что объясняется наличием у этих крыльев сужения струек и, следовательно, дополнительного разрежения на верх них концевых частях и расширения (дополнительного увеличения давления) на верх них срединных частях. Для расчета коэффициента по формуле (5. 16) используются следующие полуэм пирические подходы. 1. Расчет коэффициента трения крыла. Коэффициент трения определяется следующей формулой: (5. 17) Здесь – коэффициент одностороннего трения пластины в несжимаемом потоке; – коэффициент, учитывающий влияние относительной толщины профиля крыла на его сопротивление; – коэффициент, учитывающий влияние сжимаемости. Коэффициент одностороннего трения определяется по формулам (3. 11) … (3. 13) гл. III (рис. 3. 11). Коэффициент = 1 при М >1, а при дозвуковых скоростях находится по графику (рис. 4. 28). Коэффициент находится по графику (рис, 5. 14), как функция числа М и координа ты точки перехода.

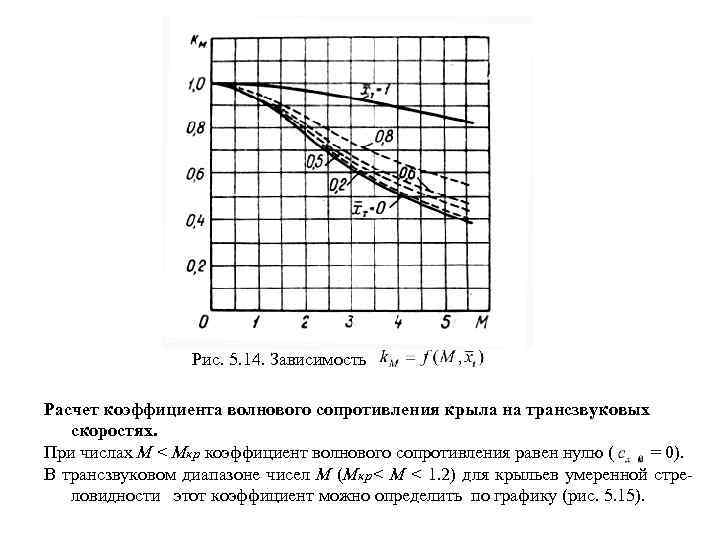Рис. 5. 14. Зависимость Расчет коэффициента волнового сопротивления крыла на трансзвуковых скоростях. При числах М < Мкр коэффициент волнового сопротивления равен нулю ( = 0). В трансзвуковом диапазоне чисел М (Мкр< М < 1. 2) для крыльев умеренной стре ловидности этот коэффициент можно определить по графику (рис. 5. 15).

Рис. 5. 15. Зависимости На этом графике Параметры от параметров подобия – удлинение крыла. и называются параметрами подобия. Найдя указанные параметры для крыла из графика рис 5. 15 искомый коэффициент, волнового сопротивления крыла определим по формуле (5. 18) Из формулы (5. 18) следует, что коэффициент в значительной степени зависит от относительной толщины профиля и уменьшается с уменьшением. Однако на может повлиять также и форма профиля. В настоящее время разра ботан так называемый суперкритический профиль, вид которого изображен на рисунке 5. 16.

Рис. 5. 16. Суперкритический профиль

6. 1 Аэродинамические характеристики тонкого профиля в сверхзвуковом потоке Рассмотрим обтекание тонкой пластинки, установленной под малым положительным углом атаки, сверхзвуковым потоком газа (рис. 5. 17). Рис. 5. 17. Обтекание тонкой пластинки сверхзвуковым потоком газа Сверхзвуковой поток, обтекая переднюю кромку пластины, разветвляется. У верхней поверхности пластины поток, расширяясь, поворачивается, а затем течет вдоль плас тинки с постоянной скоростью, большей скорости невозмущенного потока. Давление на верхней стороне пластины понижено по сравнению с давлением невозмущенного потока. Часть потока, омывающая нижнюю сторону пластины, повора чивается в районе передней кромки на тупой угол, меньший 180°, испытывает сжатие и тормозится. При этом у передней кромки со стороны нижней поверхности возникает косой скачок уплотнения.

За скачком поток течет вдоль нижней поверхности с постоянной скоростью, меньшей скорости невозмущенного потока. Давление же на нижней стороне пластинки больше давления невозмущенного потока. У задней кромки пластинки верхняя и нижняя части потока смыкаются, и поток приобретает прежнее направление. Картина обтека ния у задней кромки пластины противоположна картине обтекания у передней кром ки.

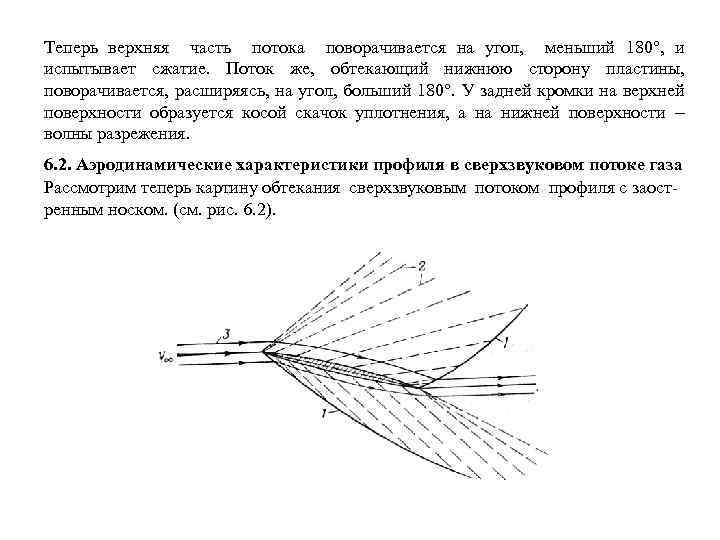Теперь верхняя часть потока поворачивается на угол, меньший 180°, и испытывает сжатие. Поток же, обтекающий нижнюю сторону пластины, поворачивается, расширяясь, на угол, больший 180°. У задней кромки на верхней поверхности образуется косой скачок уплотнения, а на нижней поверхности волны разрежения. 6. 2. Аэродинамические характеристики профиля в сверхзвуковом потоке газа Рассмотрим теперь картину обтекания сверхзвуковым потоком профиля с заост ренным носком. (см. рис. 6. 2).

Характер обтекания такого профиля определяется наклоном элемента контура профиля у его носка к направлению скорости набегающего потока. Пусть про филь установлен под углом атаки, близким к нулю При обтекании сверхзвуко вым потоком заостренного профиля можно рассчитать распределение давления по контуру профиля и определить аэродинамические силы, действующие на про филь (рис. 6. 3). Теоретически установлена зависимость между коэффициентом давления и уг лом . (3. 1) При угле атаки профиля, отличном от нуля, коэффициенты давления опреде ляются формулами, вытекающими из (6. 1).

(3. 2) Их этих выражений можно получить коэффициенты подъемной силы, волно вого сопротивления и коэффициент продольного момента симметричного про филя: (3. 3) где коэффициент В определяется как

Из формул (3. 3) можно сделать следующие выводы для тонкого профиля в слабовозмущенном сверхзвуковом потоке: 1. Все аэродинамические коэффициенты по мере роста числа М уменьшаются. 2. Коэффициенты подъемной силы и продольного момента зависят в первом приближении от формы профиля и пропорциональны углу атаки. 3. Волновое сопротивление складывается из двух частей – волнового сопротивления, пропорционального углу атаки, независящего от формы профиля и равного сопротивлению плоской пластины и сопротивления, зависящего от формы профиля и его толщины. В действительных условиях (при обтекании профиля вязким газом), кроме вол нового сопротивления, имеет место также сопротивление трения. На рис. 3. 4 приведены некоторые формы сверхзвуковых профилей: чечевицеобразный, ромбовидный и клиновидный.

Основные формы сверхзвуковых профилей. а) – чечевицеобразный; б) – ромбовидный; в) – клиновидный

На рис. 3. 5 и 3. 6 в качестве примера приведены экспериментальные зависимо сти и для ромбовидного профиля.

Лекция 7. АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРЫЛА КОНЕЧНОГО РАЗМАХА ПРИ БОЛЬШИХ ДОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ Аэродинамические характеристики крыла при трансзвуковых скоростях (числах М). Влияние стреловидности на аэродинамические характеристики крыла. Крылья изменяемой геометрии. Принципы проектирования сверхзвуковых крыльев. Литература: [1. 2], [1. 9], [1. 16], [1. 17], [1. 18]

При обтекании дозвуковым потоком крыла конечного размаха концы крыла влияют на распределение давления по всей повер хности крыла и вызывают индуктивное сопротивление, завися щее от удлинения крыла. В сверхзвуковом потоке влияние концов распространяется не на всю поверхность крыла, а лишь на некоторую ее часть, ограни ченную конусами возмущения, выходящими из концов передней кромки крыла (см. рис. 4. 1). Рис. 4. 1. Обтекание сверхзвуковым потоком газа крыла конечного размаха прямоугольной формы в плане

У крыла, имеющего прямоугольную форму в плане, влияние концов ограни чено треугольниками, отсекаемыми конусами возмущения, с углами при вер шине, равными 2 , где. Аэродинамические характеристики прямоугольной пластины конечного раз маха при фиксированном угле атаки зависят только от отношения площади треугольников, отсекаемых конусами возмущения на поверхности крыла, к общей площади крыла, т. е. от отношения (7. 1) У крыльев прямоугольной формы в плане, но различного удлинения относи тельная величина площади, на которую оказывают влияние концы крыла, не одинакова. Поэтому крылья различного удлинения при одинаковых углах ата ки имеют неодинаковое распределение давлений по поверхности крыла и разные значения коэффициентов и (крыло меньшего удлинения имеет мень шие величины коэффициентов и ). Однако при равных крыло меньшего удлинения имеет большее значение.

Значительное влияние на аэродинамические характеристики крыла конечного размаха в сверхзвуковом потоке оказывает направление передней кромки крыла относительно невозмущенного потока. Теория и экспериментальные данные показывают, что стреловидное крыло выгодно применять при сверхзвуковых скоростях полета в том случае, если крыло будет расположено внутри конуса возмущения, выходящего из точки излома передней кромки (дозвуковая кромка крыла). Таким образом, при условии (рис. 4. 2) крыло будет иметь меньшее волновое сопротивление, чем крыло прямоугольной формы в плане. Рис. 7. 2. Обтекание сверхзвуковым потоком газа стреловидного крыла

Если же обтекание стреловидного крыла таково, что (сверхзвуковая кромка, рис. 7. 2, б), то волновое сопротивление стреловидного крыла бу дет примерно таким же, как и у прямого крыла. Таким образом, передняя кромка крыла на одном числе М может быть дозвуковой, а на другом – сверхзвуковой. Следовательно, будет различной в зависимос ти от числа М и физическая картина обтекания кромки крыла (рис. 7. 3). Аналогичный вывод справедлив и для крыла треугольной формы в плане. Рис. 7. 3. Физическая картина обтекания дозвуковой (а) и сверхзвуковой (б) передних кромок крыла

7. 2. Анализ преимуществ и недостатков различных крыльев в дозвуковом, околозвуковом и сверхзвуковом потоках Рассмотрим аэродинамические характеристики , , А, Кмакс и в зависимости от числа М для двух крыльев: пря моугольногокрыла большого удлинения и стреловидного крыла малого удлинения. Зависимости для них приведены на рис. 7. 4. Рис. 7. 4. Сравнительные зависимости

У нестреловидного крыла большого удлинения наблюдается малое значение критического числа М, резкое увеличение коэффициента волнового сопротив ления на закритических числах М, достижение максимума в районе чисел М порядка единицы и последующее уменьшение по мере роста числа М. У крыла малого удлинения большой стреловидности вследствие пространст венного обтекания указанные коэффициенты сглажены. Критическое число М больше, рост коэффициента с увеличением числа М не такой значительный, как у прямого крыла, максимум сдвинут в сторону сверхзвуковых чисел М. На докритических числах М волновое сопротивление отсутствует и коэффициент в основном определяется силами трения в пограничном слое. Эти силы с увеличением числа М несколько падают. Коэффициенты прямоугольного и стреловидного крыльев при М < Мкр можно считать приблизительно одинако выми. Анализируя вышесказанное, можно сделать вывод, что для уменьшения коэф фициента на закритических числах М целесообразно делать крылья стре ловидными и уменьшать их удлинение. На больших сверхзвуковых числах М различие в величине коэффициента становится небольшим.

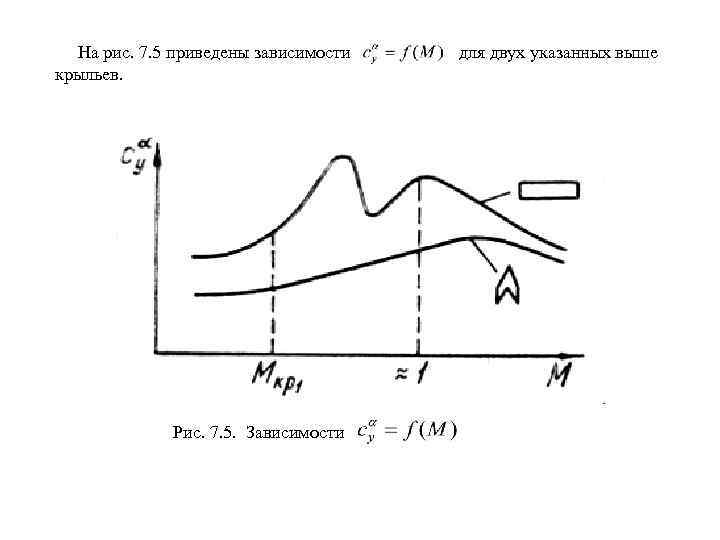На рис. 7. 5 приведены зависимости крыльев. Рис. 7. 5. Зависимости для двух указанных выше

Наблюдается заметное различие в величинах прямоугольного крыла боль шого удлинения и стреловидности и стреловидного крыла малого удлинения во всем диапазоне чисел М, за исключением больших сверхзвуковых скоростей. Кроме того, прямоугольное крыло имеет характерное падение производной на некоторых числах М в области М кр < М < 1, связанное с образованием местных сверхзвуковых зон на нижней поверхности крыла. Кривая для стреловидного крыла малого удлинения из за влияния пространственности обте кания проходит более плавно. Зависимости указанных крыльев приведены на рис. 7. 6. Рис. 7. 6. Зависимости

Для их анализа следует воспользоваться формулой , из которой следует, что коэффициент А зависит от производной и коэффициента подсасывающей силы. Если оба крыла выполнены с закругленной передней кромкой, т. е. если в обоих случаях реализуется подсасывающая сила, то и различие в зависимос тях будет определяться в основном величиной производной , которая больше у прямоугольного крыла. Поэтому коэффициент А у этого крыла меньше. Возрастание коэффициента А при числах Мкр свидетельст вует об уменьшении подсасывающей силы, а при М > 1 и об уменьшении производной. Характер уменьшения производной и подсасывающей силы на сверх звуковых числах М неодинаков для разных крыльев, поэтому характер про текания кривых в этой области чисел М может отличаться от приведенного на рис. 7. 6 (они могут быть нелинейными, и пересекаться). Зависимости для двух крыльев приведены на рис. 7. 7.

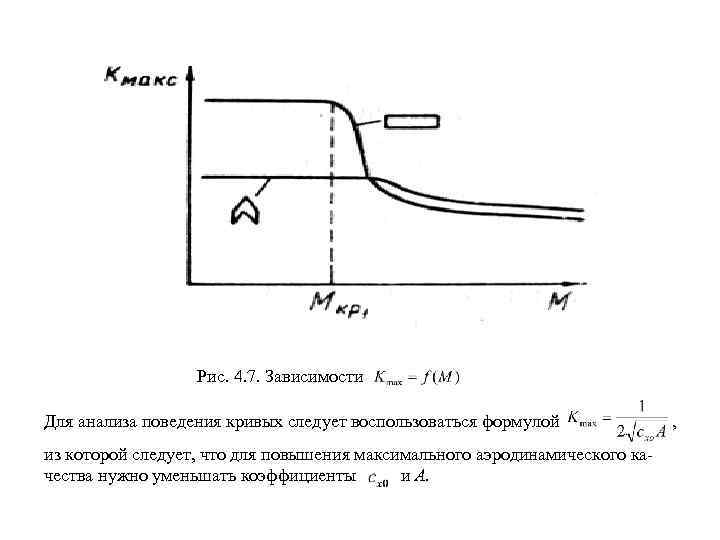Рис. 4. 7. Зависимости Для анализа поведения кривых следует воспользоваться формулой из которой следует, что для повышения максимального аэродинамического ка чества нужно уменьшать коэффициенты и А. ,

Зависимости для двух рассматриваемых крыльев будут иметь вид, показанный на рис. 7. 8. Рис. 7. 8. Зависимости Причины протекания кривых при М < 1 у прямоугольного крыла влияние сжимае мости увеличивает перепад между нижней и верхней поверхностями. Это приводит к смещению фокуса вперед. На стреловидном крыле этого не происходит. При М > 1 фокус обоих крыльев стабилизируется, после того, как заканчивается перестройка эпюр давления.

7. 3. Принципы проектирования сверхзвуковых крыльев Анализируя поведение кривых, изображенных на рис. 7. 4… 7. 8, можно сделать ряд существенных выводов, которые могут быть использованы при проектировании крыльев для ЛА. На малых дозвуковых скоростях нестреловидное крыло большого удлинения по срав нению со стреловидным крылом малого удлинения имеет лучшие несущие свойства, большие значения производной и большее аэродинамическое качество. На больших дозвуковых скоростях нестреловидное крыло большого удлинения имеет лучшие несущие свойства, но гораздо большее сопротивление по сравнению со стреловидным крылом малого удлинения. В результате с некоторого числа М качество нестреловид ного крыла становится меньше качества стреловидного крыла. На умеренных сверхзвуковых скоростях из за меньшего волнового сопротивления преимущество имеет стреловидное крыло малого удлинения, т. к. качество его выше. 7. 4. Аэродинамические характеристики крыльев изменяемой стреловидности На больших сверхзвуковых скоростях различие между характеристиками крыльев различной формы в плане уменьшается. Для того, чтобы крыло имело хорошие несущие характеристики на малых дозвуковых скоростях, малое сопротивление на околозвуковых и умеренных скоростях сверхзвукового полета, а также возможно более высокое аэродинамические качество на всех скоростях, нужно с ростом числа М менять его геометрическую форму таким образом, чтобы увеличивался угол стреловидности крыла и уменьшалось его удлинение.

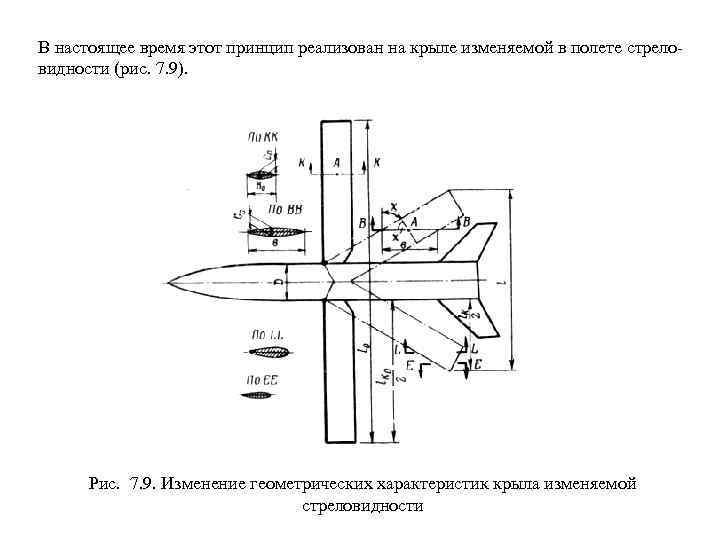В настоящее время этот принцип реализован на крыле изменяемой в полете стрело видности (рис. 7. 9). Рис. 7. 9. Изменение геометрических характеристик крыла изменяемой стреловидности

Применение крыла изменяемой стреловидности позволяет получать оптимальные аэродинамические характеристики на всех числах М полета. Например, при полетах на максимальную дальность и продолжительность, когда нужно иметь большое аэродинамическое качество, или на взлетно посадочных режимах, когда нужно иметь хорошие несущие свойства крыла, большую производную , консольная часть выдвигается вперед. При этом уменьшается угол стреловидности консольной части крыла и возрастают удлинение, относительная толщина и его площадь. Увеличение площади S происходит по причине того, что при малой стреловидности корневая часть ее выходит из центроплана. Увеличение относительной толщины объясняется тем, что с уменьшением стреловидности при неизменной толщине крыла уменьша ются хорды его сечений bсеч. По мере роста числа М полета на околозвуковых и сверхзвуковых скоростях консоль поворачивается назад. При этом увеличивается угол стреловидности крыла, уменьшается его удлинение и относительная толщина (рис. 7. 10). Рис. 7. 10. Изменение параметров при изменении угла стреловидности крыла

На рис. 7. 11 … 7. 15 приведены зависимости коэффициентов , , А, Кмакс и в зависимости от угла стреловидности консоли крыла изменяемой стреловидности для дозвуковых и сверхзвуковых чисел М. Рис. 7. 11 Коэффициент (рис. 7. 11) при М < Мкр практически не изменяется, несколько уменьшаясь из за увеличения числа Rе. При М > Мкр и особенно при М >1 коэффи циент с увеличением сильно падает, так как уменьшается волновое сопротивле ние вследствие одновременного увеличения стреловидности, уменьшения удлинения и относительной толщины.

Рис. 7. 12 Несущие свойства крыла (коэффициент ) при повороте консоли назад из за увели чения стреловидности и уменьшения удлинения падают, особенно заметно при М < 1 (рис. 7. 12). Коэффициент А при увеличении угла стреловидности возрастает, особенно интен сивно при М < 1 (рис. 7. 13), вследствие падения несущих свойств и уменьшения под сасывающей силы (с. Т).

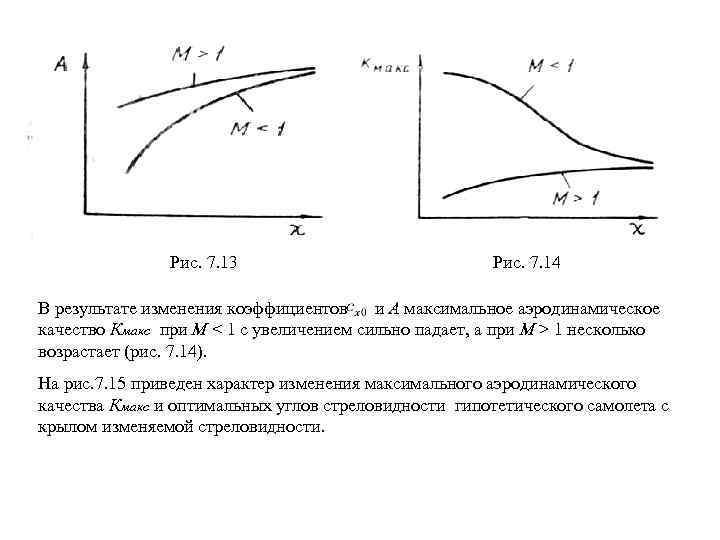Рис. 7. 13 Рис. 7. 14 В результате изменения коэффициентов и А максимальное аэродинамическое качество Кмакс при М < 1 с увеличением сильно падает, а при M > 1 несколько возрастает (рис. 7. 14). На рис. 7. 15 приведен характер изменения максимального аэродинамического качества Кмакс и оптимальных углов стреловидности гипотетического самолета с крылом изменяемой стреловидности.

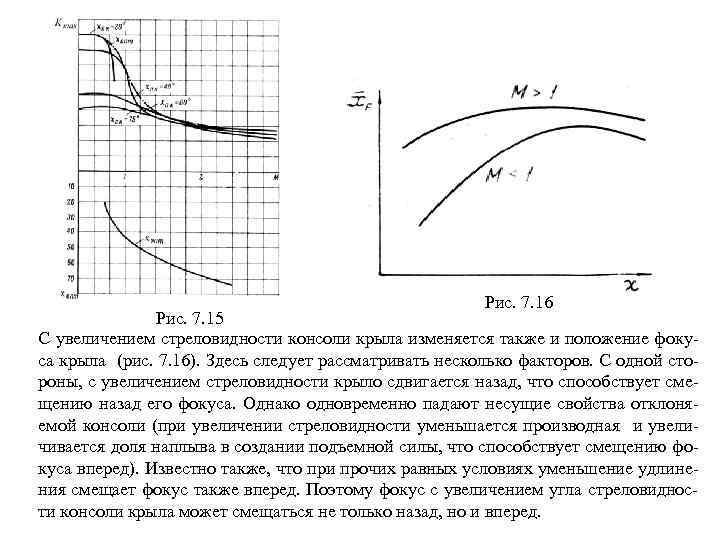Рис. 7. 16 Рис. 7. 15 С увеличением стреловидности консоли крыла изменяется также и положение фоку са крыла (рис. 7. 16). Здесь следует рассматривать несколько факторов. С одной сто роны, с увеличением стреловидности крыло сдвигается назад, что способствует сме щению назад его фокуса. Однако одновременно падают несущие свойства отклоня емой консоли (при увеличении стреловидности уменьшается производная и увели чивается доля наплыва в создании подъемной силы, что способствует смещению фо куса вперед). Известно также, что при прочих равных условиях уменьшение удлине ния смещает фокус также вперед. Поэтому фокус с увеличением угла стреловиднос ти консоли крыла может смещаться не только назад, но и вперед.