Курс лекций:

Курс лекций: 18 часов Лабораторный практикум: 18 часов Экзамен МОДЕЛИРОВАНИЕ СИСТЕМ

ЛЕКЦИЯ 1. МОДЕЛИ И МОДЕЛИРОВАНИЕ Модель и моделирование - универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания системы, процесса, явления. Моделирование - это замещение одного объекта (оригинала) другим (моделью) и фиксация и изучение свойств модели. Замещение производится с целью упрощения, удешевления, ускорения изучения свойств оригинала. Модель – представление объекта, системы или понятия (идеи) в некоторой форме, отличной от формы их реального существования. В общем случае объектом-оригиналом может быть естественная или искусственная, реальная или воображаемая система. Она имеет множество параметров S 0 и характеризуется определёнными свойствами. Количественной мерой свойств системы служит множество характеристик Y 0, система проявляет свои свойства под влиянием внешних воздействий Х.

Вид модели и методы ее исследования больше зависят от информационно - логических связей элементов и подсистем моделируемой системы, ресурсов, связей с окружением, а не от конкретного наполнения системы. Построение модели - системная задача, требующая анализа и синтеза исходных данных , гипотез, теорий, знаний специалистов. Системный подход позволяет не только построить модель реальной системы, но и использовать эту модель для оценки (например, эффективности управления, функционирования) системы. Например, отображая физическую систему на математическую систему, получим математическую модель физической системы. Любая модель строится и исследуется при определенных допущениях, гипотезах.

Пример. Рассмотрим физическую систему: тело массой m скатывающееся по наклонной плоскости с ускорением a, на которое воздействует сила F. Исследуя такие системы, Ньютон получил математическое соотношение: F = m*a. Это физико-математическая модель системы или математическая модель физической системы. При описании этой системы приняты следующие гипотезы: v поверхность идеальна (т. е. коэффициент трения равен нулю); v тело находится в вакууме (т. е. сопротивление воздуха равно нулю); v масса тела неизменна; v тело движется с одинаковым постоянным ускорением в любой точке.

Моделирование базируется на математической теории подобия, согласно которой абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании большинства систем абсолютное подобие невозможно, и основная цель моделирования - модель достаточно хорошо должна отображать функционирование моделируемой системы. По уровню, "глубине" моделирования модели бывают: v эмпирические - на основе эмпирических фактов, зависимостей; v теоретические - на основе математических описаний; v смешанные, полуэмпирические - на основе эмпирических зависимостей и математических описаний.

Проблема моделирования состоит из трех задач: v построение модели (эта задача менее формализуема и конструктивна, в том смысле, что нет алгоритма для построения моделей); v исследование модели (эта задача более формализуема, имеются методы исследования различных классов моделей); v использование модели (конструктивная и конкретизируемая задача).

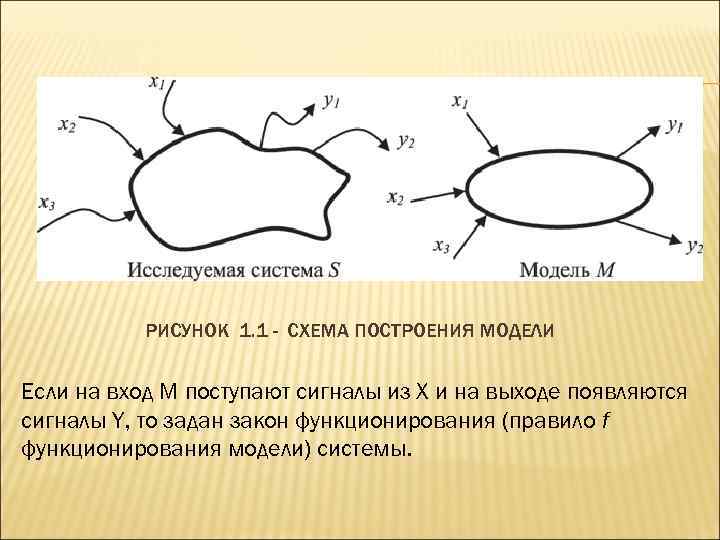
Модель М, описывающая систему S (x 1, x 2, . . . , xn; R), где Х (x 1, x 2, . . . , xn) - множество входных, выходных сигналов и состояний системы, имеет вид: М = (z 1, z 2, . . . , zm; Q), где zi є Z, i = 1, 2, . . . , n, Q, R - множества отношений над X , Z - множество описаний, представлений элементов и подмножеств X. Схема построения модели М системы S с входными сигналами X и выходными сигналами Y изображена на рисунок 1. 1.

РИСУНОК 1. 1 - СХЕМА ПОСТРОЕНИЯ МОДЕЛИ Если на вход М поступают сигналы из X и на выходе появляются сигналы Y, то задан закон функционирования (правило f функционирования модели) системы.

Моделирование - это универсальный метод получения описания функционирования объекта и использования знаний о нем. Моделирование используется в любой профессиональной деятельности Классификацию моделей проводят по различным критериям.

Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Статическая модель в каждый момент времени дает лишь "фотографию" системы, ее срез. Пример. Закон Ньютона F=a*m - это статическая модель движущейся с ускорением a материальной точки массой m. Эта модель не учитывает изменение ускорения от одной точки к другой. Модель динамическая, если среди ее параметров есть временной параметр, т. е. она отображает систему (процессы в системе) во времени Пример. Динамическая модель закона Ньютона будет иметь вид: F(t)=a(t)*m(t).

Модель дискретная, если она описывает поведение системы только в дискретные моменты времени. Пример. Если рассматривать только t=0, 1, 2, …, 10 (сек), то модель St=gt 2/2 или числовая последовательность S 0=0, S 1=g/2, S 2=2 g, S 3=9 g/2, : , S 10=50 g может служить дискретной моделью движения свободно падающего тела. Модель непрерывная, если она описывает поведение системы для всех моментов времени некоторого промежутка времени. Пример. Модель S=gt 2/2, 0 < t < 100 непрерывна на промежутке времени (0; 100).

Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели. Пример. Пусть модель экономической системы производства товаров двух видов 1 и 2, в количестве x 1 и x 2 единиц и стоимостью каждой единицы товара a 1 и a 2 на предприятии описана в виде соотношения: a 1 x 1 + a 2 x 2 = S, где S - общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, по которой можно определять (варьировать) общую стоимость S в зависимости от тех или иных значений объемов производимых товаров.

Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае - модель недетерминированная, стохастическая (вероятностная). Пример. Приведенные выше физические модели - детерминированные. Если в модели S = gt 2 / 2, 0 < t < 100 мы учли бы случайный параметр - порыв ветра с силой p при падении тела: S(p) = g(p) t 2 / 2, 0 < t < 100, то мы получили бы стохастическую модель (уже не свободного!) падения.

Модель функциональная, если она представима в виде системы каких- либо функциональных соотношений. Модель теоретико-множественная, если она представима с помощью некоторых множеств и отношений принадлежности им и между ними. Пример. Пусть задано множество X = {Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна} и отношения: Николай - супруг Елены, Екатерина - супруга Петра, Татьяна - дочь Николая и Елены, Михаил - сын Петра и Екатерины, семьи Михаила и Петра дружат друг с другом. Тогда множество X и множество перечисленных отношений Y могут служить теоретико- множественной моделью двух дружественных семей.

Модель алгоритмическая , если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование, развитие. Модель структурная , если она представима структурой данных или структурами данных и отношениями между ними. Например, структурной моделью может служить описание (табличное, графическое, функциональное или другое) структуры системы. Модель графовая, если она представима графом или графами и отношениями между ними.

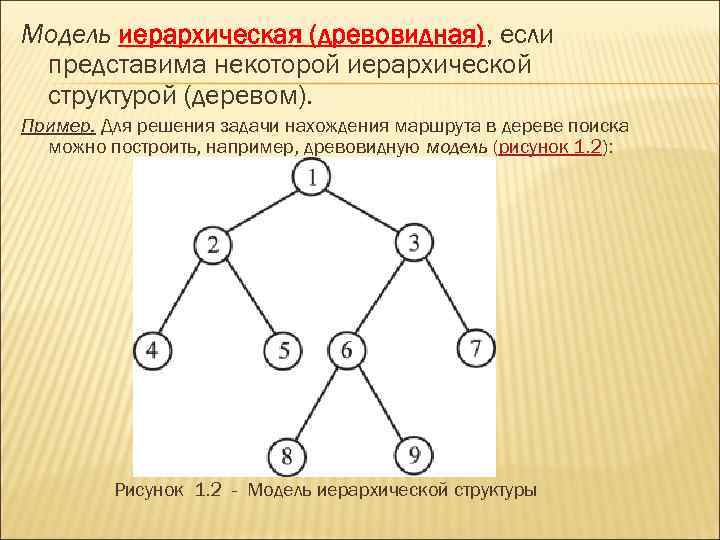
Модель иерархическая (древовидная), если представима некоторой иерархической структурой (деревом). Пример. Для решения задачи нахождения маршрута в дереве поиска можно построить, например, древовидную модель (рисунок 1. 2): Рисунок 1. 2 - Модель иерархической структуры

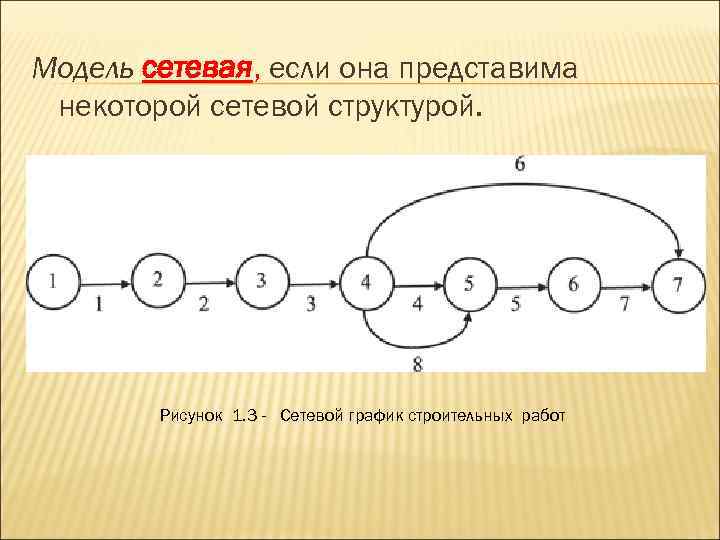
Модель сетевая, если она представима некоторой сетевой структурой. Рисунок 1. 3 - Сетевой график строительных работ

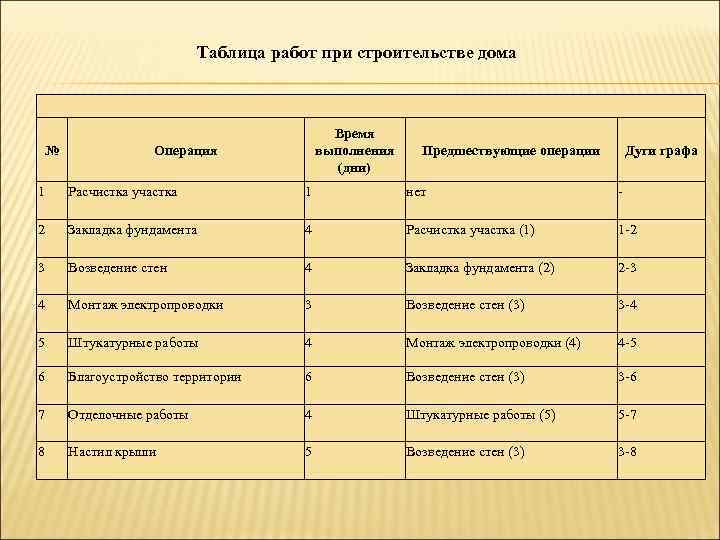
Таблица работ при строительстве дома Время № Операция выполнения Предшествующие операции Дуги графа (дни) 1 Расчистка участка 1 нет 2 Закладка фундамента 4 Расчистка участка (1) 1 2 3 Возведение стен 4 Закладка фундамента (2) 2 3 4 Монтаж электропроводки 3 Возведение стен (3) 3 4 5 Штукатурные работы 4 Монтаж электропроводки (4) 4 5 6 Благоустройство территории 6 Возведение стен (3) 3 6 7 Отделочные работы 4 Штукатурные работы (5) 5 7 8 Настил крыши 5 Возведение стен (3) 3 8

ЛЕКЦИЯ 2. ОСНОВНЫЕ СВОЙСТВА МОДЕЛИ И МОДЕЛИРОВАНИЯ Тип модели зависит от информационной сущности моделируемой системы, от связей и отношений ее подсистем и элементов, а не от ее физической природы. Как правило модель включает в себя: объект О, субъект (не обязательный) А, задачу Z, ресурсы B, среду моделирования С. Модель можно представить формально в виде: М = < O, Z, A, B, C >.

ОСНОВНЫЕ СВОЙСТВА ЛЮБОЙ МОДЕЛИ v целенаправленность; v конечность; v упрощенность; v приблизительность; v адекватность; v наглядность, обозримость основных ее свойств и отношений; v доступность и технологичность для исследования или воспроизведения; v информативность;

ОСНОВНЫЕ СВОЙСТВА ЛЮБОЙ МОДЕЛИ: v сохранение информации, содержавшейся в оригинале; v полнота ; v устойчивость; ; v целостность; v замкнутость; v адаптивность; v Управляемость; v возможность развития моделей (предыдущего уровня).

ЖИЗНЕННЫЙ ЦИКЛ МОДЕЛИРУЕМОЙ СИСТЕМЫ: v сбор информации об объекте, выдвижение гипотез, предварительный модельный анализ; v проектирование структуры и состава моделей (подмоделей); v построение спецификаций модели, разработка и отладка отдельных подмоделей, сборка модели в целом, идентификация (если это нужно) параметров моделей; v исследование модели - выбор метода исследования и разработка алгоритма (программы) моделирования; v исследование адекватности, устойчивости, чувствительности модели; v оценка средств моделирования (затраченных ресурсов); v интерпретация, анализ результатов моделирования и установление некоторых причинно-следственных связей в исследуемой системе; v генерация отчетов и проектных (народно-хозяйственных) решений; v уточнение, модификация модели, если это необходимо, и возврат к исследуемой системе с новыми знаниями, полученными с помощью модели и моделирования.

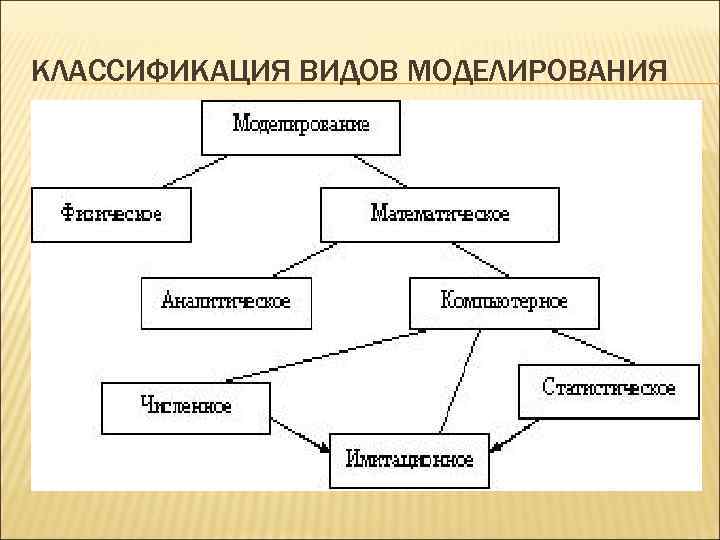
КЛАССИФИКАЦИЯ ВИДОВ МОДЕЛИРОВАНИЯ

При физическом моделировании используется сама система, либо подобная ей в виде макета, например, летательный аппарат в аэродинамической трубе. Математическое моделирование есть процесс установления соответствия реальной системы S математической модели M и исследование этой модели, позволяющее получить характеристики реальной системы. При аналитическом моделировании процессы функционирования элементов записываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и др. ).

Компьютерное – математическое моделирование формулируется в виде алгоритма (программы для ЭВМ), что позволяет проводить над ней вычислительные эксперименты. Численное моделирование использует методы вычислительной математики. Статистическое моделирование использует обработку данных о системе с целью получения статистических характеристик системы. Имитационное моделирование воспроизводит на ЭВМ (имитирует) процесс функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени. Применение математического моделирования позволяет исследовать объекты, реальные эксперименты над которыми затруднены или невозможны.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛОЖНЫХ СИСТЕМ В общем виде систему математически можно представить в виде: Будем считать, что элемент s есть некоторый объект, обладающий определенными свойствами, внутреннее строение которого для целей исследования не играет роли, например, самолет для моделирования полета – не элемент, а для моделирования работы аэропорта – элемент. Связь l между элементами есть процесс их взаимодействия, важный для целей исследования. Система S – совокупность элементов со связями l и целью функционирования F. Сложная система – это система, состоящая из разнотипных элементов с разнотипными связями. Большая система – это система, состоящая из большого числа однотипных элементов с однотипными связями.

Автоматизированная система SA есть сложная система с определяющей ролью элементов двух типов: технических средств Sт и действий человека SH: здесь остальные элементы системы. Структура системы есть разбиение (декомпозиция) системы на элементы или группы элементов с указанием связей между ними, неизменными во время функционирования системы.

Состояние – это множество характеристик элементов системы, изменяющихся во времени и важных для целей ее функционирования. Процесс (динамика) – это множество значений состояний системы, изменяющихся во времени. Цель функционирования есть задача получения желаемого состояния системы. Целенаправленное вмешательство в процесс функционирования системы называется управлением.

Задачи исследования систем: Анализ – изучение свойств функционирования системы. Синтез – выбор структуры и параметров по заданным свойствам системы. Пусть T = [ t 0, t 1] есть временной интервал моделирования системы S (интервал модельного времени). Построение модели начинается с определения параметров и переменных, определяющих процесс функционирования системы. Параметры системы это характеристики системы, остающиеся постоянными на всем интервале T.

Переменные бывают зависимые и независимые. Независимые переменные есть входные воздействия (экзогенные) (в том числе управляющие) ; ими могут быть также воздействия внешней среды. Последовательность изменения x(t) при называется фазовой траекторией системы , , где X – пространство состояний или фазовое пространство. Последовательность изменения y(t) называется выходной траекторией системы. Зависимые переменные есть выходные характеристики (сигналы) (эндогенные).

Основные подходы к построению ММ систем Имеет место цепочка: описательная модель → математическая схема→ имитационная модель. При построении ММ системы S необходимо решить вопрос о её полноте. Полнота моделирования регулируется выбором границ «Система S — Среда Е»

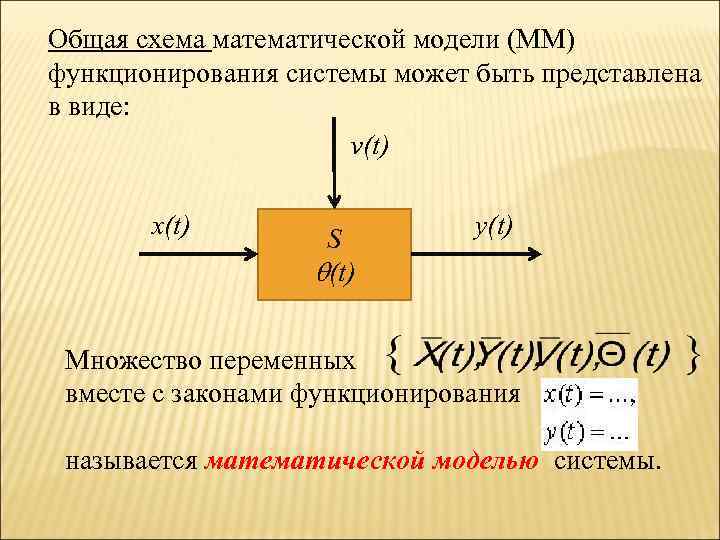
Общая схема математической модели (ММ) функционирования системы может быть представлена в виде: v(t) х(t) S y(t) (t) Множество переменных вместе с законами функционирования называется математической моделью системы.

Процесс функционирования S описывается оператором FS: выходная траектория; FS закон функционирования S. FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил. Алгоритм функционирования AS — метод получения выходных характеристик с учётом входных воздействий Х(t).

Соотношение (1) является математическим описанием поведения объекта S моделирования во времени t, т. е. отражает его динамические свойства. (1) это динамическая модель системы S. Для статических условий ММ есть отображения X, V, H в Y, т. е. (2) Соотношения (1), (2) могут быть заданы формулами, таблицами и т. д.

Состояния системы S характеризуются векторами: и где в момент tl (t 0, T) в момент tll (t 0, T) и т. д. к=1…n. Z. Z 1(t), Z 2(t)… Zk(t) это координаты точки в к мерном фазовом пространстве. Совокупность всех возможных значений состояний { } называется пространством состояний объекта моделирования Z, причём zk Z.

Состояние системы S в интервале времени t 0

Если t непрерывно, то модель называется непрерывной, иначе – дискретной: . Если модель не содержит случайных элементов, то она называется детерминированной , в противном случае – вероятностной. Если математическое описание модели слишком сложное и частично или полностью неопределенно, то в этом случае используются агрегативные модели. Сущность агрегативной модели заключается в разбиении системы на конечное число взаимосвязанных частей (подсистем), каждая из которых допускает стандартное математическое описание. Эти подсистемы называются агрегатами.

ЛЕКЦИЯ 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ НЕПРЕРЫВНО ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ (Д - СХЕМЫ) Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции но их производные различных порядков. Математическое соотношение для детерминированных систем в общем виде: (7).

Например, процесс малых колебаний маятника описан обыкновенными дифференциальным уравнением: где m 1, l 1 масса, длина подвески маятника, угол отклонения маятника от положения равновесия. Из этого уравнения можно найти оценки интересующих характеристик, например период колебаний Дифференциальные уравнения, или Д схемы, являются математическим аппаратом теории систем автоматического регулирования, управления.

Следует отметить, что часто используемые в САУ системы диф. уравнений определяются путём линеаризацией управления объекта (системы), более сложного вида, имеющего нелинейности:

ДИСКРЕТНО – ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ (F-СХЕМЫ) Дискретно-детерминированные модели (F-схемы) являются предметом рассмотрения теории автоматов (ТА). Конечный автомат имеет множество внутренних состояний и входных сигналов, являющихся конечными множествами. Автомат задаётся F- схемой: F=, (1) где z , x , y - соответственно конечные множества входных, выходных сигналов (алфавитов) и конечное множество внутренних состояний (алфавита). z 0 Z - начальное состояние; (z, x) - функция переходов; (z, x) - функция выхода.

В момент t , будучи в состоянии z ( t ), автомат способен воспринять сигнал x(t) и выдать сигнал y(t)= [z(t), x(t)], переходя в состояние z(t+1)= [z(t), z(t)], z(t) Z; y(t) Y; x(t) X. Абстрактный КА в начальном состоянии z 0 принимая сигналы x(0), x(1), x(2) … выдаёт сигналы y(0), y(1), y(2)… (выходное слово).

Существуют F-автомат 1 -ого рода (Мили), функционирующий по схеме: z(t+1)= [z(t), z(t)], t=0, 1, 2… (1) y(t)= [z(t), x(t)], t=0, 1, 2… (2) F-автомат 2 -ого рода (Мура): z(t+1)= [z(t), z(t)], t=0, 1, 2… (3) y(t)= [z(t), x(t-1)], t=1, 2, 3… (4) Автомат 2 -ого рода, для которого y(t)= [z(t)], t=0, 1, 2, … (5) т. е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.

Т. о. уравнения 1 -5 полностью задающие F- автомат, являются частным случаем уравнения (6) где - вектор состояния, - - вектор независимых входных переменных, - - вектор воздействий внешней среды, - - вектор собственных внутренних параметров системы, - - вектор начального состояния, - t - время; и уравнения (7) когда система S - детерминированная и на её вход поступает дискретный сигнал x.

По числу состояний конечные автоматы бывают с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом согласно (2), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x ( t ) определённый выходной сигнал y ( t ), т. е. реализует логическую функцию вида: y(t)= [x(t)], t=0, 1, 2, … Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов x и y состоят из 2 -х букв.

По характеру отсчёта времени (дискретному) F- автоматы делятся на синхронные и асинхронные. В синхронных автоматах моменты времени, в которые автомат "считывает" входные сигналы, определяются принудительно синхронизирующими сигналами. Реакция автомата на каждое значение входного сигнала заканчивается за один такт синхронизации. Асинхронный F - автомат считывает входной сигнал непрерывно и поэтому, реагируя на достаточно длинный водной сигнал постоянной величины x , он может, как это следует из (1)-(5), несколько раз изменить своё состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое. Для задания работы F - автоматов наиболее часто используются : табличный, графический матричный способ.

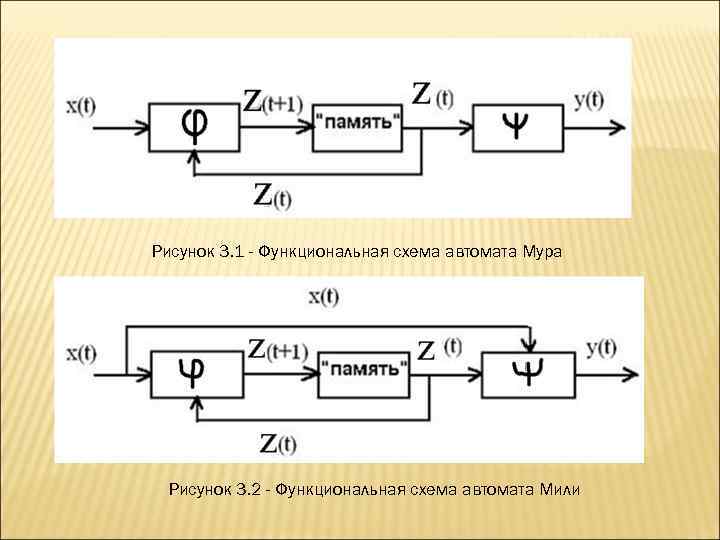
Рисунок 3. 1 - Функциональная схема автомата Мура Рисунок 3. 2 - Функциональная схема автомата Мили

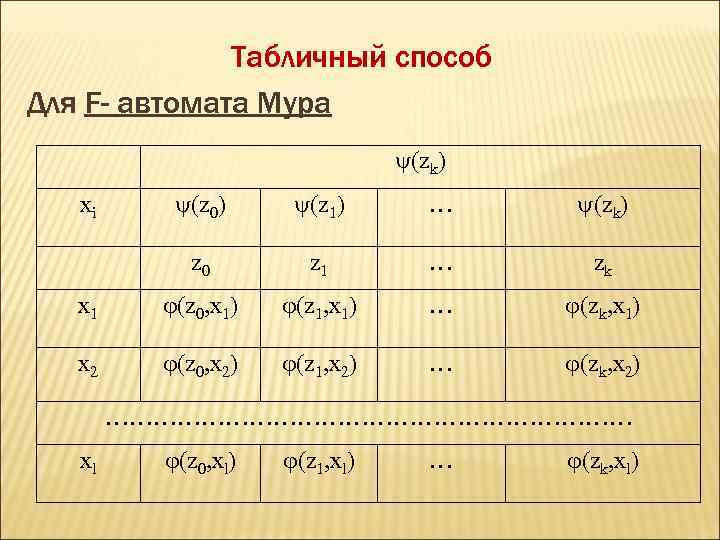
Табличный способ Для F- автомата Мура (zk) xi (z 0) (z 1) … (zk) z 0 z 1 … zk x 1 (z 0, x 1) (z 1, x 1) … (zk, x 1) x 2 (z 0, x 2) (z 1, x 2) … (zk, x 2) …………………………… xl (z 0, xl) (z 1, xl) … (zk, xl)

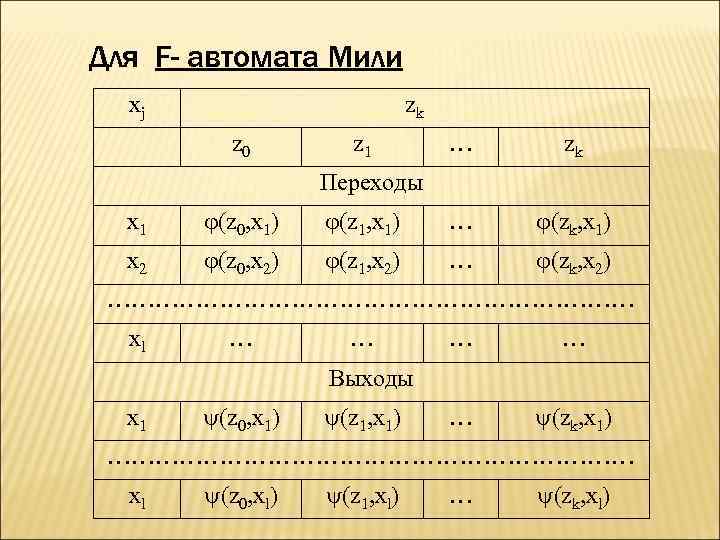
Для F- автомата Мили xj zk z 0 z 1 … zk Переходы x 1 (z 0, x 1) (z 1, x 1) … (zk, x 1) x 2 (z 0, x 2) (z 1, x 2) … (zk, x 2) …………………………… xl … … … Выходы x 1 (z 0, x 1) (z 1, x 1) … (zk, x 1) …………………………… xl (z 0, xl) (z 1, xl) … (zk, xl)

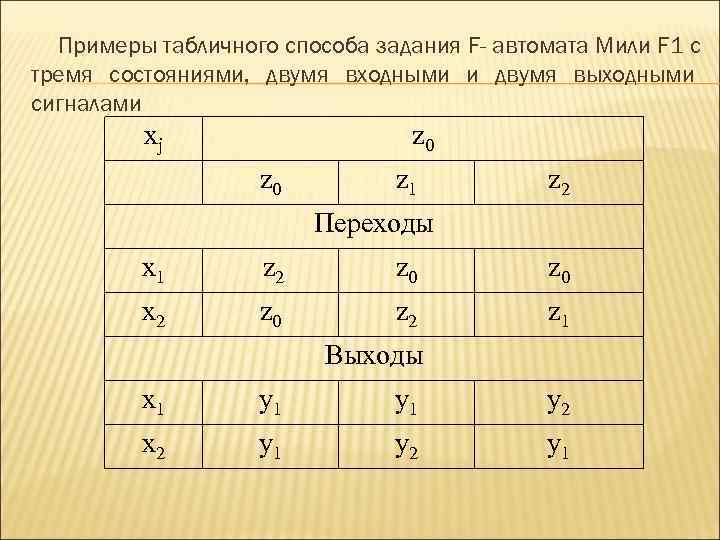
Примеры табличного способа задания F- автомата Мили F 1 с тремя состояниями, двумя входными и двумя выходными сигналами xj z 0 z 1 z 2 Переходы x 1 z 2 z 0 x 2 z 0 z 2 z 1 Выходы x 1 y 2 x 2 y 1 y 2 y 1

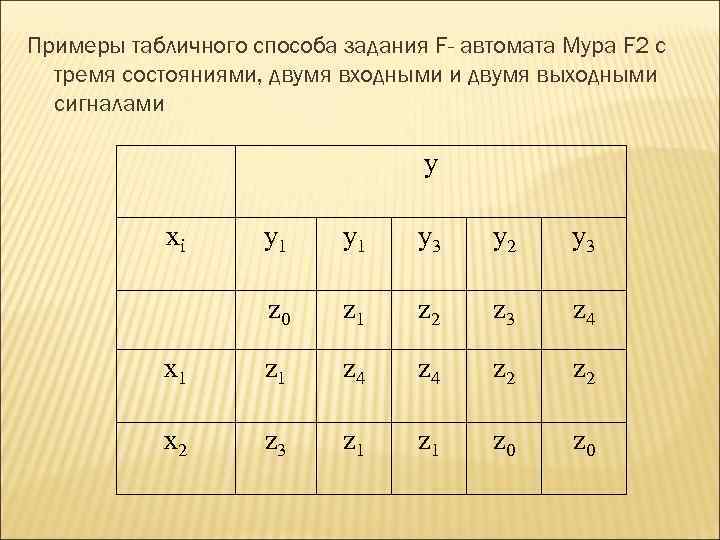
Примеры табличного способа задания F- автомата Мура F 2 с тремя состояниями, двумя входными и двумя выходными сигналами y xi y 1 y 3 y 2 y 3 z 0 z 1 z 2 z 3 z 4 x 1 z 4 z 4 z 2 x 2 z 3 z 1 z 0

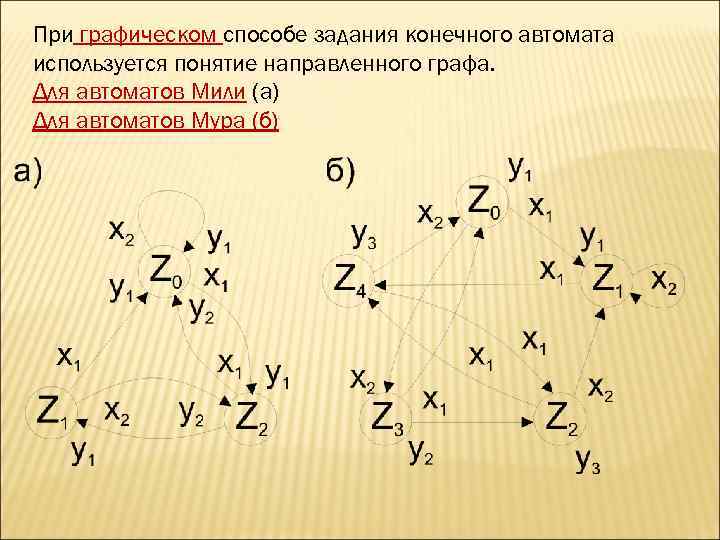
При графическом способе задания конечного автомата используется понятие направленного графа. Для автоматов Мили (а) Для автоматов Мура (б)

Матричная форма Матрица соединений автомата есть квадратная матрица С=|| cij ||, строки - исходные состояния, столбцы - состояниям перехода.

Элемент c ij = x k / y S в случае F- автомата Мили соответству входному сигналу x k , вызывающему переход из состояния z i в состояние z j и выходному сигналу y S , выдаваемому при этом переходе. Для F -автомата Мура элемент c ij равен множеству входных сигналов на переходе ( z i z j ), а выход описывается вектором выходов: i-ая компонента которого выходной сигнал, отмечающий состояние zi

Для автомата Мили F 1 Для автомата Мура F 2 матрица состояний и вектор выходов

Для детерминированных автоматов переходы однозначны. Применительно к графическому способу задания F- автомата это означает, что в графе F-автомата из любой вершины не могут выходить 2 и более ребра, отмеченные одним и тем же входным сигналом. В матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза.

Рассмотрим асинхронный F-автомат Мура y xi y 1 y 2 y 3 z 0 z 1 z 2 x 1 z 1 x 2 z 1 z 2 x 3 z 0 z 2

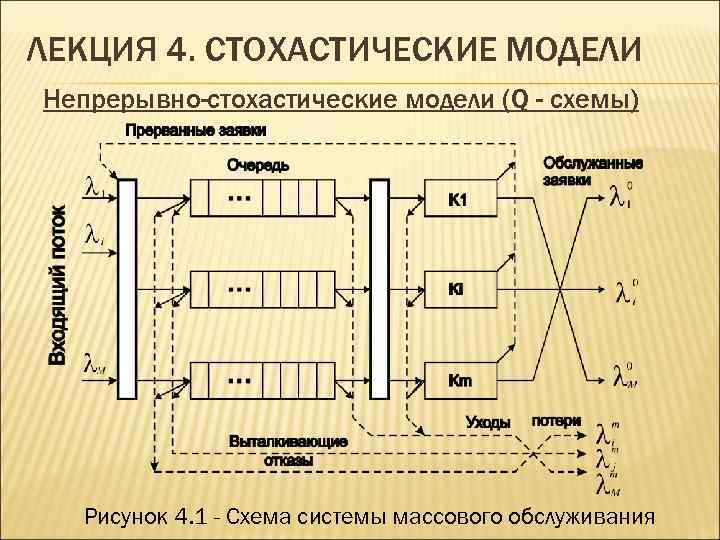
ЛЕКЦИЯ 4. СТОХАСТИЧЕСКИЕ МОДЕЛИ Непрерывно-стохастические модели (Q - схемы) Рисунок 4. 1 - Схема системы массового обслуживания

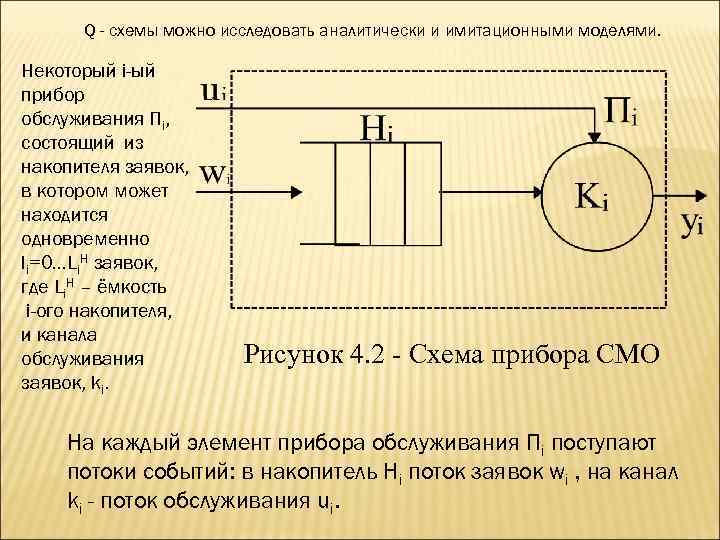
Q - схемы можно исследовать аналитически и имитационными моделями. Некоторый i-ый прибор обслуживания Пi, состоящий из накопителя заявок, в котором может находится одновременно li=0…Li. H заявок, где Li. H – ёмкость i-ого накопителя, и канала обслуживания Рисунок 4. 2 Схема прибора СМО заявок, ki. На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi поток заявок wi , на канал ki - поток обслуживания ui.

Потоком событий (ПС) называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Однородный ПС характеризуется только моментами поступления этих событий (вызывающими моментами) и задаётся последовательностью {tn}={0 t 1 t 2… tn …}, где tn - момент поступления n- ого события - неотрицательное вещественное число. ОПС может быть также задан в виде последовательности промежутков времени между n-ым и n-1 -ым событиями { n}. Неоднородным ПС называется последовательность {tn, fn} , где tn- вызывающие моменты; fn- набор признаков события.

Рассмотрим ОПС, для которого i { n} случайные величины, независимые между собой. Тогда ПС называется потоком с ограниченным последействием. ПС называется ординарным , если вероятность того, что на малый интервал времени t, примыкающий к моменту времени t попадает больше одного события Р 1 ( t , t ) пренебрежительн мала. Если для любого интервала t событие P 0(t, t) + P 1(t, t) + Р 1(t, t)=1, P 1(t, t) вероятность попадания на интервал t ровно одного события. Для ординарного потока событий P 0(t, t) + P 1(t, t) 1, Р 1(t, t)= ( t), где ( t) величина, порядок малости который выше, чем t, т. е. lim( ( t))=0 при t 0.

Стационарным ПС называется поток, для которого вероятность появления того или иного числа событий на интервале времени зависит от длины этого участка и не зависит от того, где на оси времени 0 t взят этот участок. Для ОПС справедливо: 0*P 0(t, t) + 1*P 1(t, t)= P 1(t, t) среднее число событий на интервале t. Среднее число событий, наступающих на участке t в единицу времени составляет P 1(t, t)/ t. Рассмотрим предел этого выражения при t 0 lim P 1(t, t)/ t= (t)*(1/един. вр. ). Если этот предел существует, то он называется интенсивностью (плотностью) ОПС. Для стандартного ПС (t)= =const.

Заявки, обслуженные каналом k i и заявки, покинувшие прибор П i по различным причинам не обслуженными, образуют выходной поток y i Y. Процесс функционирования П i можно представить как процесс изменения состояний его элементов во времени Z i (t). Переход в новое состояние для П i означает изменение кол-ва заявок, которые в нём находятся (в канале k i и накопителе H i ). . вектор состояний для Пi имеет вид : где - состояния накопителя, ( =0 - накопитель пуст, =1 - в накопителе одна заявка…, = - накопитель занят полностью; - состояние канала ki ( =0 - канал свободен, =1 канал занят).

Q -схемы реальных объектов образуются композицией многих элементарных приборов обслуживания Пi. Если k i различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема). Если приборы П i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Т. о. для задания Q -схемы необходимо оператор сопряжения R , отражающий взаимосвязь элементов структуры. Связи в Q -схеме изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой выходной поток не может снова поступить на какой-либо элемент, т. е. обратная связь отсутствует.

Собственными (внутренними) параметрами Q- схемы будут являться: - количество фаз LФ, - количество каналов в каждой фазе, Lkj, j=1… LФ, - количество накопителей каждой фазы Lkj, k=1… LФ, - ёмкость i-ого накопителя Li. H. В зависимости от ёмкости накопителя различают: системы с потерями (Li. H=0, накопитель отсутствует); системы с ожиданием (Li. H ); системы с ограниченной ёмкостью накопителя Нi (смешанные). Обозначим всю совокупность собственных параметров Q-схемы как подмножество Н.

В зависимости от динамики приоритетов Q-схемы различают статические и динамические. Статические приоритеты назначаются заранее и не зависят от состояний Q -схемы, т. е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании. Исходя из правил выбора заявок из накопитель Н i на обслуживание каналом k i можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н, ожидает окончания обслуживания представляющей заявки каналом k i и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель, прерывает обслуживание каналом ki заявки с более низким приоритетом и сами занимает канал (при этом вытесненная из k i заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Н i).

Необходимо также знать набор правил, по которым заявки покидают Нi и ki: для Н i – либо правила переполнения, либо правила ухода, связанные с истечением времени ожидания заявки в Нi ; для ki – правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале ki, т. е. правила блокировок канала. При этом различают блокировки ki по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q ‑ схеме, регулирующих поток заявок в зависимости от её состояния. Набор возможных алгоритмов поведения заявок в Q ‑ схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А. Т. о. Q‑схема, описывающая процесс функционирования СМО любой сложности однозначно задаётся в виде набора множеств: Q = .

ЛЕКЦИЯ 5. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ Метод ИМ заключается в создании логико-аналитической (математической модели системы и внешних воздействий), имитации функционирования системы, т. е. в определении временных изменений состояния системы под влиянием внешних воздействий и в поучении выборок значений выходных параметров, по которым определяются их основные вероятностные характеристики. Имитационное моделирование (ИМ) — это метод исследования, который основан на том, что анализируемая динамическая система заменяется имитатором и с ним производятся эксперименты для получения об изучаемой системе. Роль имитатора зачастую выполняет программа ЭВМ. Данное определение справедливо для стохастических систем.

Модель системы со структурным принципом управления представляет собой совокупность моделей элементов и их функциональные взаимосвязи. Модель элемента (агрегата, обслуживающего прибора) – это набор правил (алгоритмов) поведения устройства по отношению к выходным воздействиям (заявкам) и правил изменений состояний элемента. Элемент отображает функциональное устройство на том или ином уровне детализации.

Пусть необходимо определить функцию распределения случайной величины y. Допустим, что искомая величина y может быть представлена в виде зависимости: y=f( , где случайные величины с известными функциями распределения.

Для решения задач такого вида применяется следующий алгоритм: 1) по каждой из величин производится случайное испытание, в результате каждого определяется некоторое конкретное значение случайной величины i i i; 2) используя найденные величины, определяется одно частное значение yi по выше приведённой зависимости; 3) предыдущие операции повторяются N раз, в результате чего определяется N значений случайной величины y; 4) на основании N значений величины находится её эмпирическая функция распределения.

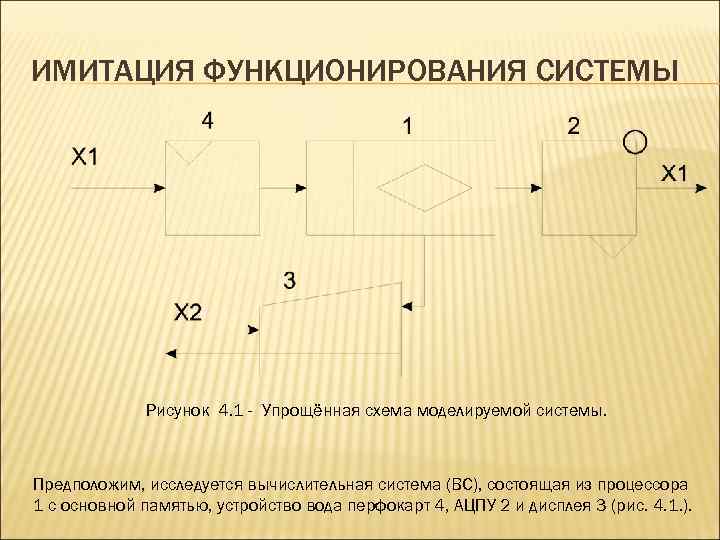
ИМИТАЦИЯ ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ Рисунок 4. 1 - Упрощённая схема моделируемой системы. Предположим, исследуется вычислительная система (ВС), состоящая из процессора 1 с основной памятью, устройство вода перфокарт 4, АЦПУ 2 и дисплея 3 (рис. 4. 1. ).

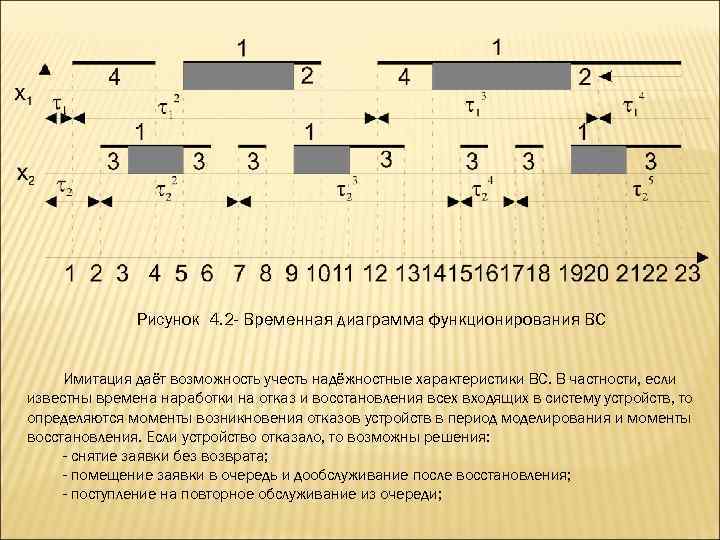
Рисунок 4. 2 - Временная диаграмма функционирования ВС Имитация даёт возможность учесть надёжностные характеристики ВС. В частности, если известны времена наработки на отказ и восстановления всех входящих в систему устройств, то определяются моменты возникновения отказов устройств в период моделирования и моменты восстановления. Если устройство отказало, то возможны решения: - снятие заявки без возврата; - помещение заявки в очередь и дообслуживание после восстановления; - поступление на повторное обслуживание из очереди;

ЛЕКЦИЯ 5. ОБОБЩЁННЫЕ АЛГОРИТМЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ 5. 1 Алгоритм моделирования по принципу особых состояний Оно использовалось в приведённом выше примере. В качестве событий выделены: поступление заявки в систему; освобождение элемента после обслуживания заявки; завершения моделирования; другие типы событий.

Простой циклический алгоритм моделированиясводится к следующим действиям: 1) определяется событие с минимальным временем — наиболее раннее событие; 2) модельному времени присваивается значение времени наступления наиболее раннего события; 3) определяется тип события; 4) в зависимости от типа события предпринимаются действия, направленные на загрузку устройств и продвижение заявок в соответствии с алгоритмом их обработки, и вычисляются моменты наступления будущих событий; эти действия называют реакцией модели на события; 5) перечисленные действия повторяются до истечения времени моделирования. В процессе моделирования производится измерение и статистическая обработка значений выходных характеристик.

Рисунок 5. 1 - Обобщённый алгоритм моделирования систем по принципу особых состояний

5. 2 АЛГОРИТМ МОДЕЛИРОВАНИЯ ПО ПРИНЦИПУ t. Рисунок 5. 2 - Обобщённый алгоритм моделирования систем по принципу приращений " t"

ЛЕКЦИЯ 6. МЕТОДЫ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК МОДЕЛИРУЕМЫХ СИСТЕМ. 6. 1 Измеряемые характеристики моделируемых систем. При статистическом моделировании большая часть характеристик — это случайные величины. По каждой такой характеристике y определяется N значений, по которым строится гистограмма относительных частот, вычисляется математическое ожидание, дисперсия и моменты более высокого порядка, определяются средние по времени и максимальные значения. Коэффициенты загрузки устройств вычисляются по формуле: k=Vk*Nok/Tm (1) Vk среднее время обслуживания одной заявки к ым устройством; Nok - количество обслуженных заявок устройством за время моделирования Tm.

6. 2 РАСЧЁТ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ ВЫХОДНОЙ ХАРАКТЕРИСТИКИ В случае стационарного эргодического процесса функционирования системы вычисление М(у) и Д(у) выходной характеристики у производится усреднением не по времени, а по множеству N знач. , измеренных по одной реализации достаточной длительности. В целях экономии ОЗУ ЭВМ М(у) и Д(у) вычисляются по рекуррентным формулам: mn=mn 1*(n 1)/n + y/n; (2) где m n 1 математическое ожидание, вычисленное на предыдущем шаге. dn=dn 1*(n 2)/(n 1) + 1/n*(yn mn 1)2 (3) здесь dn 1 дисперсия, вычисленная на предыдущем шаге. При большом количестве измерений эти оценки являются состоятельными и несмещёнными.

6. 3 РАСЧЁТ СРЕДНЕГО ПО ВРЕМЕНИ ЗНАЧЕНИЯ ВЫХОДНОЙ ХАРАКТЕРИСТИКИ Средняя длина очереди к каждому устройству вычисляется по формуле: (4) где i номер очередного изменения состояния очереди (занесение заявки в очередь или исключение из очереди); N количество изменений состояния очереди; интервал времени между двумя последними изменениями очереди. Ёмкость накопитель: (5) ёмкость накопителя, занятая в интервале между двумя последними обращениями к накопителю для ввода вывода заявки.

6. 4 ПОСТРОЕНИЕ ГИСТОГРАММЫ ДЛЯ СТАЦИОНАРНОЙ СИСТЕМЫ

ЛЕКЦИЯ 7. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ 7. 1 Особенности моделирования случайных событий Пусть имеются случайные числа x i , т. е. возможные значения случайной величины , равномерно распределённой в интервале {0, 1}. Необходимо реализовать случайное событие А, наступающее с заданной вероятностью Р. Определим А как событие, состоящее в том, что выбранное значение x i удовлетворяет неравенству: Р xi (1)

. . Тогда вероятность события А будет : (2) Противоположное событию А состоит в том, что xi >р. Тогда Пусть А 1, А 2…Аn – полная группа событий, наступающая с вероятностями Р 1, Р 2, … Рn соответственно. Определим Аm как событие, состоящее в том, что выбранное значение xi случайной величины удовлетворяет неравенству: lm 1

Пусть независимые события А и В имеют вероятности наступления Р А и Р В. Возможными исходами совместных испытаний в этом случае будут события с вероятностями Р А Р В , (1 Р А )Р В , Р А (1 Р В ), (1 Р А )(1 Р В моделирования совместных испытаний можно использовать последовательную проверку условия (1). Он требует двух чисел xi. Рассмотрим случай, когда события А и В являются зависимыми и наступают с вероятностями РА и РВ. Обозначим через Р(В/А) условную вероятность события В при условии, что событие А произошло. Cобытие А произошло: xmPA, то произошло событие

Поэтому для испытания, связанного с событием В необходимо определить вероятность: Выберем из совокупности {Xi число xm+1 и проверим } справедливость неравенства В зависимости от того, выполняется оно или нет, получаем исход испытания. Алгоритм вычислений можно представить в виде схемы

7. 2 ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН

7. 3 ВЫЧИСЛЕНИЕ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

7. 4 МОДЕЛИРОВАНИЕ НОРМАЛЬНО РАСПРЕДЕЛЁННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Y Оно может быть осуществлено на основании центральной предельной теоремы, согласно которой закон распределения суммы независимых случайных величин стремится к нормальному с увеличением числа слагаемых Получение случайной величины с различными распределениями.