Курс Исследование операций Теория и практика моделирования Лекция

Скачать презентацию Курс Исследование операций Теория и практика моделирования Лекция

Лекция по спец. предмету.ppt

Количество слайдов: 92

Курс: Исследование операций. Теория и практика моделирования Лекция 1. Основные понятия системного анализа и исследования операций. Понятие моделирования. Классификация математических моделей. Прямая и обратная задача. Линейное программирование

Гносеологической основой* системного анализа является общая теория систем (ОТС), основу которой положил австралийский биолог Д. Берталанфи. Причины возникновения ОТС • Потребность в ОТС: – потребность в языке междисциплинарного обмена знаниями • физика - химия - биология (начало XX в. ) • экономика - социология - психология (середина XX в. ) • экономика - биология - термодинамика (конец XX в. ) До XX в. в качестве междисциплинарного формализованного языка использовалась математика, но её изобразительных средств недостаточно для эффективного переноса знаний между вышеуказанными дисциплинам. • Предпосылки возникновения ОТС: – достижения формальной логики в XIX в. – отдельные научные дисциплины достигли уровня развития, позволившего обнаружить в них общие подходы и схожие теории (начало XX в. ) – возникновение теории информации (начало XX в. ) – возникновение формальной лингвистики и языков программирования (XX в. ) Предназначение системного анализа – поиск структурного сходства законов, установленных в различны дисциплинах (предметных областях), исходя из которых можно вывести общесистемные закономерности. *гносеология –раздел философии, изучающий формы и методы научного познания

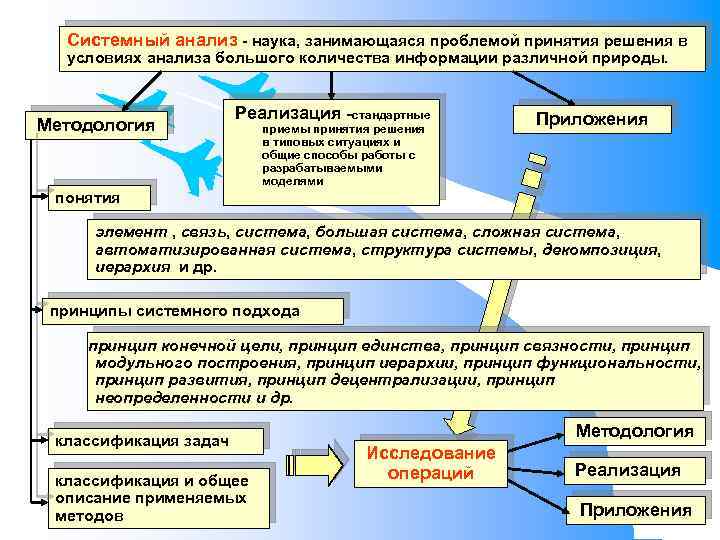Системный анализ наука, занимающаяся проблемой принятия решения в условиях анализа большого количества информации различной природы. Методология Реализация стандартные приемы принятия решения в типовых ситуациях и общие способы работы с разрабатываемыми моделями Приложения понятия элемент , связь, система, большая система, сложная система, автоматизированная система, структура системы, декомпозиция, иерархия и др. принципы системного подхода принцип конечной цели, принцип единства, принцип связности, принцип модульного построения, принцип иерархии, принцип функциональности, принцип развития, принцип децентрализации, принцип неопределенности и др. классификация задач классификация и общее описание применяемых методов Методология Исследование операций Реализация Приложения

Предмет теории систем. Определение системы Предмет теории систем - системы произвольной природы • Общепринятого определения системы • Имеющиеся определения отличаются степенью общности и границами применимости • Понятие системы происходит от древнегреческого корня, обозначающего сочетание, организм, организацию, союз; подразумевало порядок, присущий именуемому явлению. Вербальные определения Берталанфи: комплекс элементов, находящихся во взаимодействии Холл, Фейджин: множество объектов вместе с отношениями между объектами и между их атрибутами Получившее наибольшее распространение: совокупность взаимосвязанных и целесообразно взаимодействующих элементов

Предмет теории систем. Определение системы • Формальные определения: – {X, Q}, где X - множество переменных, Q - множество отношений между переменными – {T, x, u, y, Г, η, φ}, где: • Т - множество моментов времени; • x - вектор переменных состояния, причём x(t 2) = φ(x(t 1), u(t 1), t 2), где {t 1, t 2} T; • u - вектор входных переменных; • y - вектор выходных переменных, причём y(t 2) = η(x(t 1), u(t 1), t 2); • Г - множество допустимых выходных векторов.

Основные понятия системного анализа Элемент некоторый объект (материальный, энергетический, информационный), который обладает рядом важных для нас свойств, но внутреннее строение (содержание) которого безотносительно к цели рассмотрения Связь - важный для целей рассмотрения обмен между элементами веществом, энергией, информацией Система совокупность элементов, которая обладает следующими признаками: связями, которые позволяют посредством переходов по ним от элемента к элементу соединить два любых элемента совокупности; свойством, отличным от свойств отдельных элементов совокупности. Большая система, которая включает значительное число однотипных элементов и однотипных связей. Сложная система, которая состоит из элементов разных типов и обладает разнородными связями между ними. В качестве примера можно привести ЭВМ, самолет или систему ПВО на направлении. Автоматизированная система сложная система с определяющей ролью элементов двух типов: в виде технических средств, в виде действия человека Структура системы расчленение системы на группы элементов с указанием связей между ними, неизменное на все время рассмотрения и дающее представление о системе в целом. Указанное расчленение может иметь материальную, функциональную, алгоритмическую или другую основу. Декомпозиция деление системы на части, удобное для каких либо операций с этой системой. Иерархия - структура с наличием подчиненности, т. е. неравноправных связей между элементами, когда воздействие в одном из направлений оказывают гораздо большее влияние на элемент, чем в другом. Виды иерархических структур разнообразны, но важных для практики иерархических структур всего две древовидная и ромбовидная назад

Элемент – неделимая часть системы, обладающая самостоятельностью по отношению к данной системе. Неделимость элемента рассматривается как нецелесообразность учёта в пределах модели данной системы его внутреннего строения. Сам элемент характеризуется только его внешними проявлениями в виде связей и взаимосвязей с остальными элементами. Множество А элементов системы можно описать в виде A = {ai}, i = 1, . . . , n, где аi – i-й элемент системы; п – число элементов в системе.

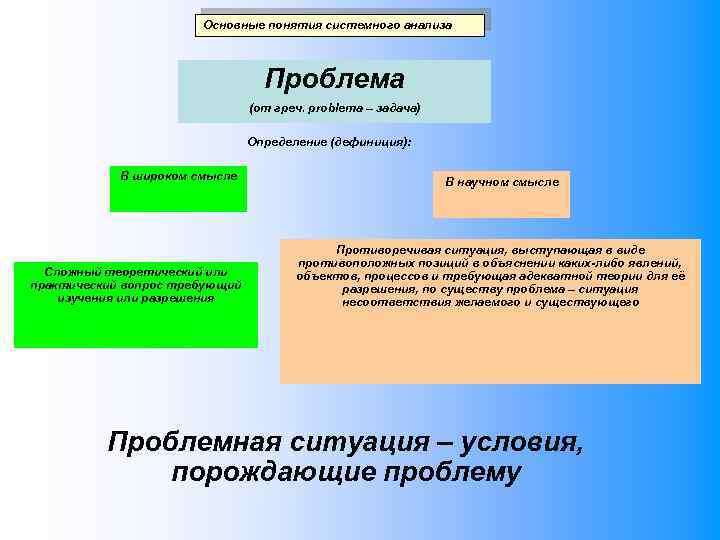Основные понятия системного анализа Проблема (от греч. problema – задача) Определение (дефиниция): В широком смысле Сложный теоретический или практический вопрос требующий изучения или разрешения В научном смысле Противоречивая ситуация, выступающая в виде противоположных позиций в объяснении каких-либо явлений, объектов, процессов и требующая адекватной теории для её разрешения, по существу проблема – ситуация несоответствия желаемого и существующего Проблемная ситуация – условия, порождающие проблему

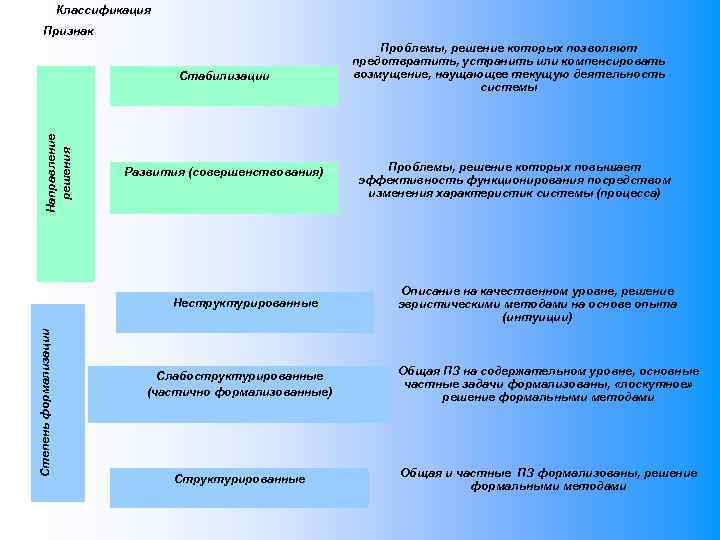Классификация Признак Направление решения Стабилизации Развития (совершенствования) Степень формализации Неструктурированные Проблемы, решение которых позволяют предотвратить, устранить или компенсировать возмущение, наущающее текущую деятельность системы Проблемы, решение которых повышает эффективность функционирования посредством изменения характеристик системы (процесса) Описание на качественном уровне, решение эвристическими методами на основе опыта (интуиции) Слабоструктурированные (частично формализованные) Общая ПЗ на содержательном уровне, основные частные задачи формализованы, «лоскутное» решение формальными методами Структурированные Общая и частные ПЗ формализованы, решение формальными методами

Классификация (обобщение) Проблемы, решение которых позволяют предотвратить, устранить или компенсировать возмущение, наущающее текущую деятельность системы. Структурированные проблемы Стабилизации Развития (совершенствования) Инновационные Проблемы, решение которых повышает эффективность функционирования посредством изменения характеристик системы (процесса). Слабо структурированные проблемы Проблемы, решение которых связано с разработкой новых идей и внедрением нововведений. Слабо структурированные и неструктурированные проблемы Задача анализа – определение свойств системы по известной структуре Задача синтеза – определение структуры системы по её свойствам

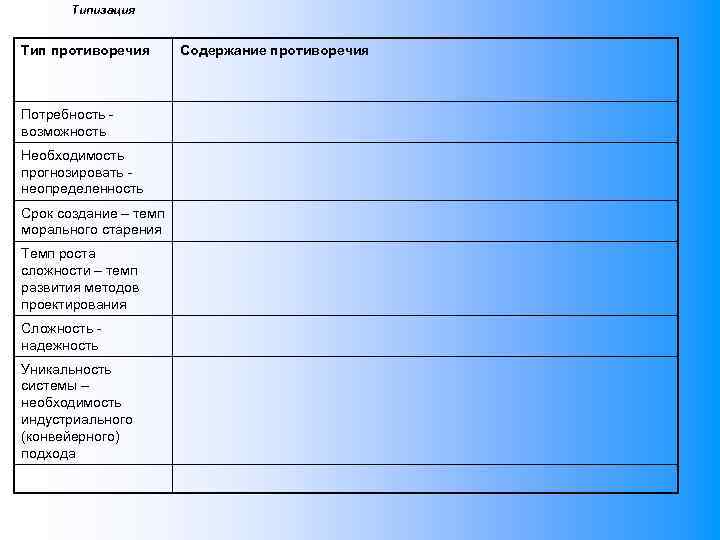Типизация Тип противоречия Потребность возможность Необходимость прогнозировать неопределенность Срок создание – темп морального старения Темп роста сложности – темп развития методов проектирования Сложность надежность Уникальность системы – необходимость индустриального (конвейерного) подхода Содержание противоречия

Системный подход Изучение объектов (процессов, явлений) как систем вызвало формирование нового подхода в науке – системного подхода В настоящее время при анализе и синтезе сложных систем получил развитие системный подход, который отличается от классического (или индуктивного) подхода. Согласно последнему, система рассматривается с позиций перехода от частного к общему и синтезирует (конструирует) систему путём слияния её элементов, разрабатываемых раздельно. Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель, причём исследуемый объект выделяется из окружающей среды. Системный подход – подход к исследованию объектов (процессов, явлений) как к системам, в которых выделены элементы, внутренние и внешние связи, наиболее существенным образом влияющие на результаты его функционирования, а цели каждого элемента определены исходя из общего предназначения. Системный подход позволяет решить проблему построения сложной системы с учётом всех факторов и возможностей, пропорциональных их значимости, на всех этапах исследования системы и построения её модели. Системный подход означает, что каждая система является интегрированным целым даже тогда, когда она состоит из отдельных разобщённых подсистем. Таким образом, в основе системного подхода лежит рассмотрение системы как интегрированного целого, причём это рассмотрение при разработке начинается с главного: формулировки цели функционирования.

Системный подход основывается на ряде законов и категорий диалектики Законы диалектики 1. Закон 2. Закон 3. Закон Категории диалектики 1. Категория 11. Категория

Основные принципы системного подхода Принцип конечной цели: абсолютный приоритет конечной цели; цель – образ желаемого будущего, т. е. модель состояния, на реализацию которого направлена деятельность Принцип единства: совместное рассмотрение системы как целого и как совокупности элементов; Принцип связности: рассмотрение любой части совместно с ее связями с окружением; Принцип модульного построения: полезно выделение модулей в системе и рассмотрение ее как совокупности модулей; Принцип иерархии: полезно введение иерархии элементов и (или) их ранжирование; Принцип функциональности: совместное рассмотрение структуры и функции с приоритетом функции над структурой; Принцип развития: учет изменяемости системы, ее способности к развитию, расширению, замене частей, накапливанию информации; Принцип децентрализации: сочетание в принимаемых решениях и управлении централизации и децентрализации; Принцип неопределенности: учет неопределенностей и случайностей в системе; Принцип эмерджентности: целое на равно сумме частей…

Исследование операций наука, занимающаяся проблемой принятия решения в условиях анализа большого количества информации различной природы. Методология понятия Реализация стандартные приемы принятия решения в типовых ситуациях и общие способы работы с разрабатываемыми моделями Приложения Операция, цель исследования операций, решение, элемент решения, множество допустимых решений (ОДР), эффективность, показатель эффективности, критерий, лицо принимающее решение (ЛПР), оптимальное решение и др. классификация показателей и критериев оценки классификация задач методы Математическое (линейное, целочисленное, динамическое, нелинейное, стохастическое и др. ) программирование, МДС, методы теории игр, теории графов и т. д.

Задача линейного программирования Целевая функция: Ограничения: Граничные условия:

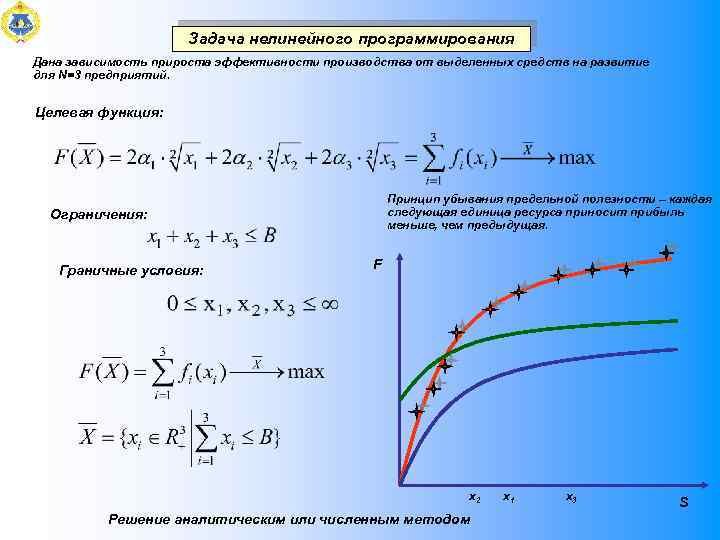Задача нелинейного программирования Дана зависимость прироста эффективности производства от выделенных средств на развитие для N=3 предприятий. Целевая функция: Принцип убывания предельной полезности – каждая следующая единица ресурса приносит прибыль меньше, чем предыдущая. Ограничения: Граничные условия: F х2 Решение аналитическим или численным методом х1 х3 S

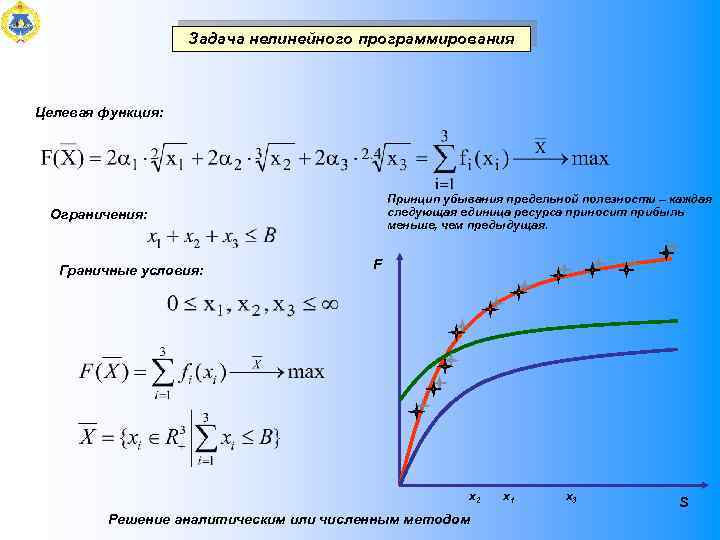Задача нелинейного программирования Целевая функция: Принцип убывания предельной полезности – каждая следующая единица ресурса приносит прибыль меньше, чем предыдущая. Ограничения: Граничные условия: F х2 Решение аналитическим или численным методом х1 х3 S

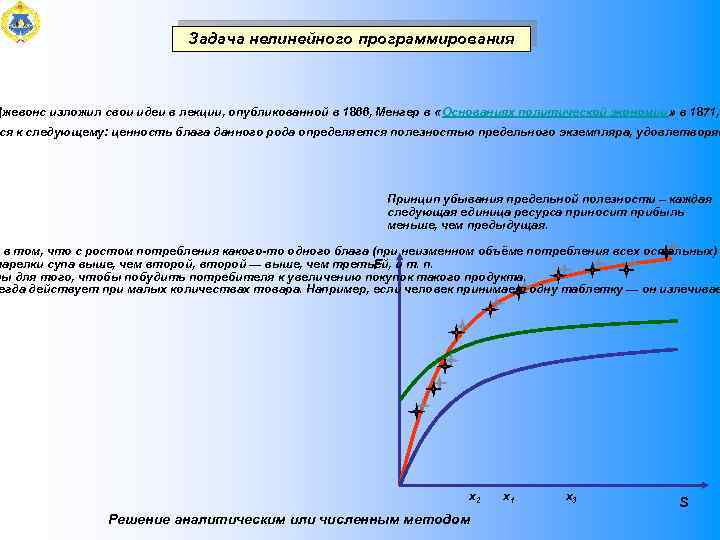Задача нелинейного программирования Джевонс изложил свои идеи в лекции, опубликованной в 1866, Менгер в « Основаниях политической экономии» в 1871, ся к следующему: ценность блага данного рода определяется полезностью предельного экземпляра, удовлетворяю Принцип убывания предельной полезности – каждая следующая единица ресурса приносит прибыль меньше, чем предыдущая. в том, что с ростом потребления какого-то одного блага (при неизменном объёме потребления всех остальных) тарелки супа выше, чем второй, второй — выше, чем третьей, и т. п. F ны для того, чтобы побудить потребителя к увеличению покупок такого продукта. егда действует при малых количествах товара. Например, если человек принимает одну таблетку — он излечивае х2 Решение аналитическим или численным методом х1 х3 S

Оптимизация распределения ресурса численным методом // Ввод исходных данных While (В > 0) { max=0; For (i=1; i<=N; i++) { d. F(i)=k(i)* (sqrt(x(i)+dx) sqrt(x(i))) If (d. F(i) > max) { max = d. F(i); Imax = i; } B=B dx; // B =dx; x(Imax) = x(Imax) + dx; // x(Imax)+=dx; } // Вывод результата (распределение ресурса)

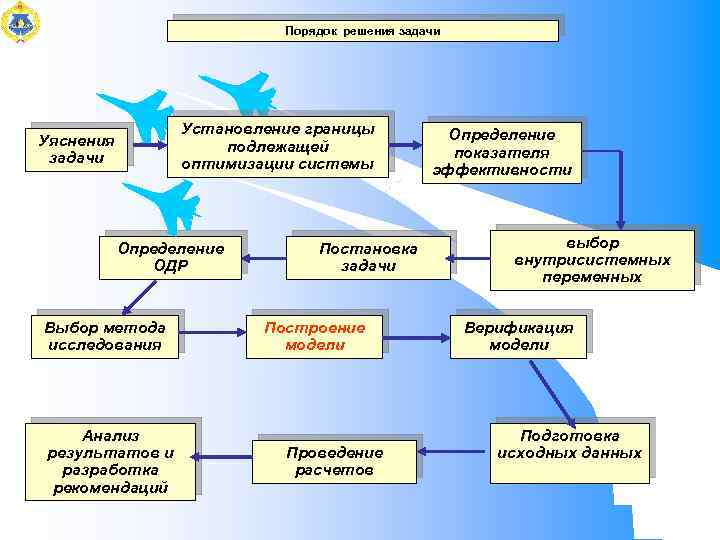Порядок решения задачи Уяснения задачи Установление границы подлежащей оптимизации системы Определение ОДР Выбор метода исследования Анализ результатов и разработка рекомендаций Постановка задачи Построение модели Проведение расчетов Определение показателя эффективности выбор внутрисистемных переменных Верификация модели Подготовка исходных данных

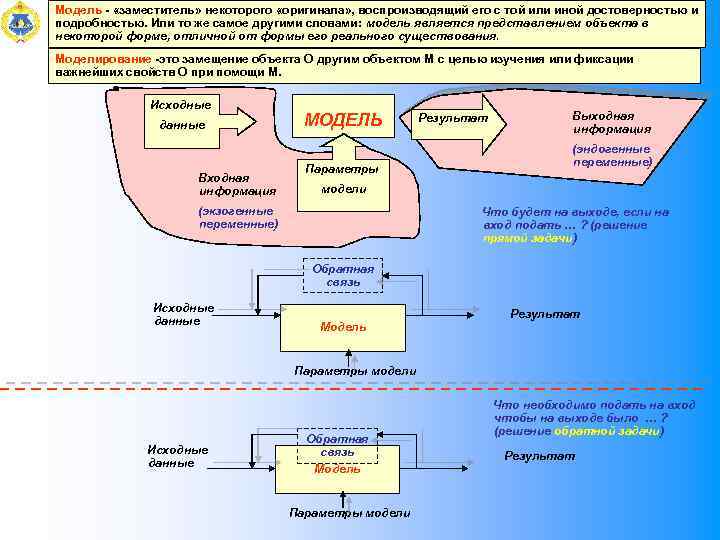Модель «заместитель» некоторого «оригинала» , воспроизводящий его с той или иной достоверностью и подробностью. Или то же самое другими словами: модель является представлением объекта в некоторой форме, отличной от формы его реального существования. Моделирование это замещение объекта О другим объектом М с целью изучения или фиксации важнейших свойств О при помощи М. Исходные данные Входная информация МОДЕЛЬ Параметры Результат Выходная информация (эндогенные переменные) модели (экзогенные переменные) Что будет на выходе, если на вход подать … ? (решение прямой задачи) Обратная связь Исходные данные Модель Результат Параметры модели Исходные данные Обратная связь Модель Параметры модели Что необходимо подать на вход чтобы на выходе было … ? (решение обратной задачи) Результат

5. Методы теории систем

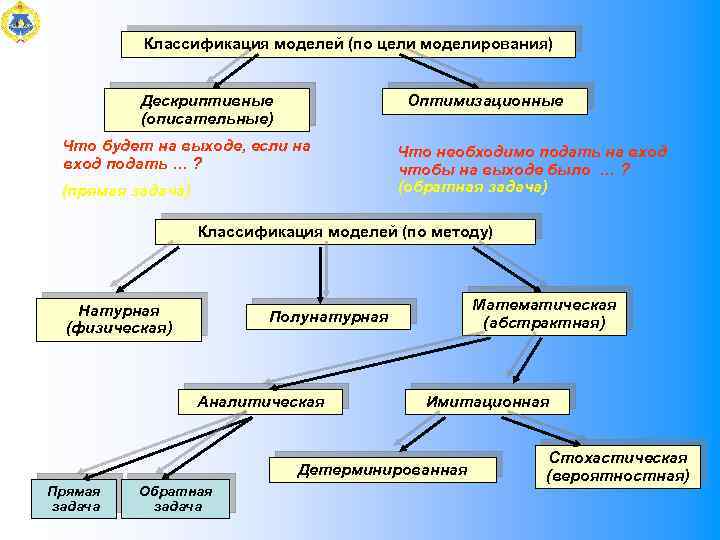Классификация моделей (по цели моделирования) Дескриптивные (описательные) Оптимизационные Что будет на выходе, если на вход подать … ? (прямая задача) Что необходимо подать на вход чтобы на выходе было … ? (обратная задача) Классификация моделей (по методу) Натурная (физическая) Математическая (абстрактная) Полунатурная Аналитическая Имитационная Детерминированная Прямая задача Обратная задача Стохастическая (вероятностная)

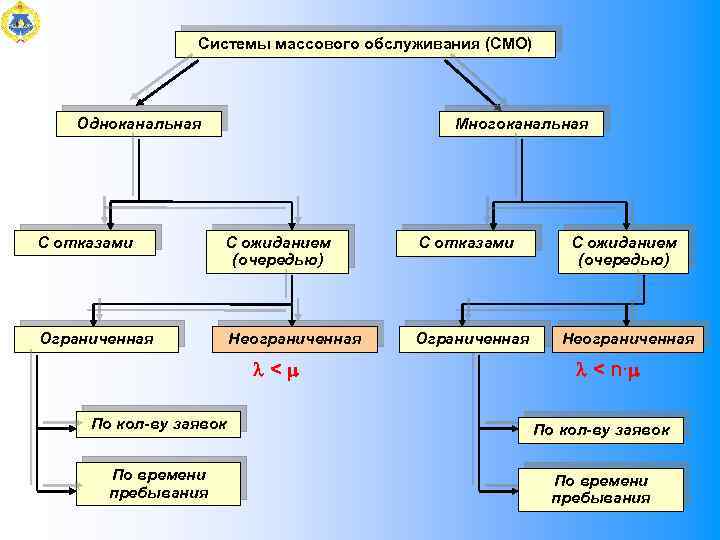Системы массового обслуживания (СМО) Одноканальная Многоканальная С отказами С ожиданием (очередью) С отказами Ограниченная Неограниченная Ограниченная < С ожиданием (очередью) Неограниченная < n· По кол-ву заявок По времени пребывания

Понятие изоморфизма Изоморфизм – сходство формы при качественном различии содержания Закон Ома для электрического тока Закон Фурье для теплового потока Закон Дарси для скорости фильтрации жидкости через пористую среду Закон Кулона Закон всемирного тяготения Моделирование различных колебательных процессов

Демонстрация аналитической модели на примере динамики биологических популяций Модель Мальтуса: Модель Ферхюльста (логистическое уравнение):

Пример аналитической модели (продолжение) Для того и щука в реке, чтоб карась не дремал Поговорка Модель Вольтерра (модель «хищник жертва» ) Межвидовая конкуренция (модель «хищник» )

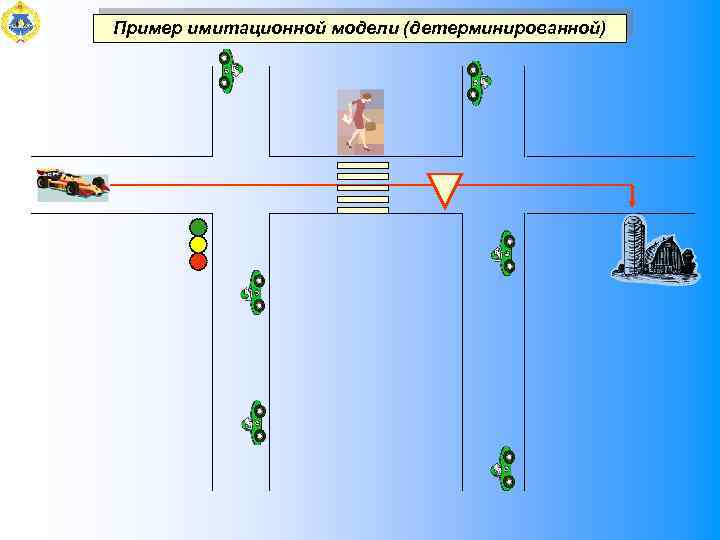Пример имитационной модели (детерминированной)

Метод статистических испытаний Program Telefon; var tr, i, k, t, kotk, traz, tsvob: integer; sost: string; tzv: array [ 0. . 72 ] of integer; Begin sost: ='Свободен'; tzv[0]: =0; {заполняю массив, сформируем массив моментов времени, в которые будут совершаться звонки} For i: =1 to 72 do tzv[i]: =tzv[i-1] + random(11) + 5; k: =1; kotk: =0; For t: =1 to 360 do Begin If t=tzv[k] then begin if sost='Занят' then kotk: =kotk + 1 else Begin sost: ='Занят'; traz: =random(6) + 5; tsvob: =t + traz; end; k: =k+1; end; If (sost='Занят') and (t=tsvob) then sost: ='Свободен'; end; write (kotk/(k-1): 10: 5); end.

Метод статистических испытаний Program Telefon; var tr, i, k, t, kotk, traz, tsvob: integer; sost: string; tzv: array [ 0. . 70 ] of integer; stek: array [ 1. . 7 ] of boolean; Begin {заполняю массив, сформируем массив моментов времени, в которые будут совершаться звонки} For i: =1 to 70 do tzv[i]: =tzv[i-1] + random(11) + 5; sost: ='Свободен'; tzv[0]: =0; k: =1; kotk: =0; stek: = true; For t: =1 to 360 do Begin If t=tzv[k] then begin if sost='Занят‘ then if stek[1] = false then kotk: =kotk + 1 else Begin stek[1]: = false; trazstek: = random(6) + 5; end else Begin sost: ='Занят'; traz: =random(6) + 5; tsvob: =t + traz; end; k: =k+1; end; If (sost='Занят') and (t=tsvob) then If stek[1] = true then sost: =' Свободен'; else Begin stek[1]= true; tsvob: =t + trazstek; end; write (kotk/(k-1): 10: 5); end.

Пример имитационной модели (стохастической) Танк А Танк B Дано: РАB = 0. 07 Р BА = 0. 12 SА = 6 выстр. /мин SB = 4 выстр. /мин BА = 28 выстр BВ = 20 выстр

For k : = 1 to 1 000 do Begin Sost. A : = ‘Жив’; Sost. B : = ‘Жив’; Ba : = 28; Bb : = 20; t: = 0; While (Sost. A = ‘Жив’) and (Sost. B = ‘Жив’) and ((Ba > 0) or (Bb > 0)) do Begin t: = t +1; If (t mod 10 = 0) and (Ba >0) then If Random <= Pab then Sost. B : = ‘Убит’ еlse Ba : = Ba 1; End If (t mod 15 = 0) and (Bb >0) then If Random <= Pba then Sost. A : = ‘Убит’ еlse Bb : = Bb 1; If (Sost. A = ‘Жив’) and (Sost. B = ‘Жив’) then col 00 : = col 00 +1; If (Sost. A = ‘Жив’) and (Sost. B = ‘Убит’) then col 01 : = col 01 +1; If (Sost. A = ‘Убит’) and (Sost. B = ‘Жив’) then col 10 : = col 10 +1; If (Sost. A = ‘Убит’) and (Sost. B = ‘Убит’) then col 11 : = col 11 +1; End Метод статистических испытаний

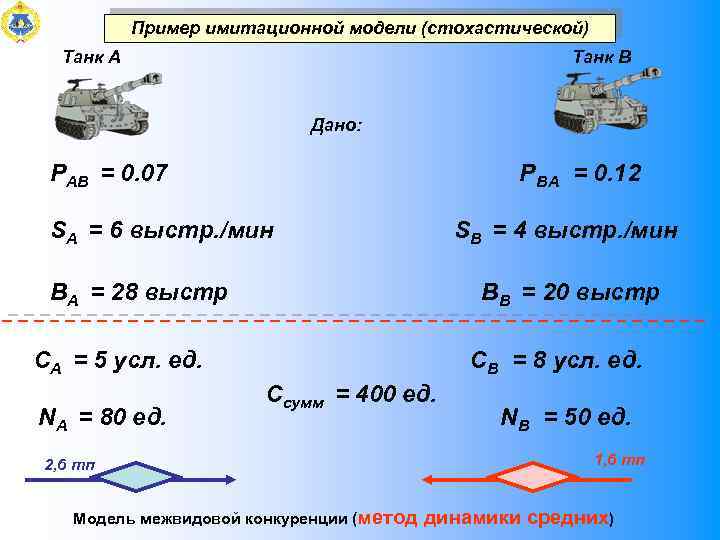Пример имитационной модели (стохастической) Танк А Танк B Дано: РАB = 0. 07 Р BА = 0. 12 SА = 6 выстр. /мин SB = 4 выстр. /мин BА = 28 выстр BВ = 20 выстр СА = 5 усл. ед. С В = 8 усл. ед. Ссумм = 400 ед. NА = 80 ед. NВ = 50 ед. 2, 6 тп 1, 6 тп Модель межвидовой конкуренции (метод динамики средних)

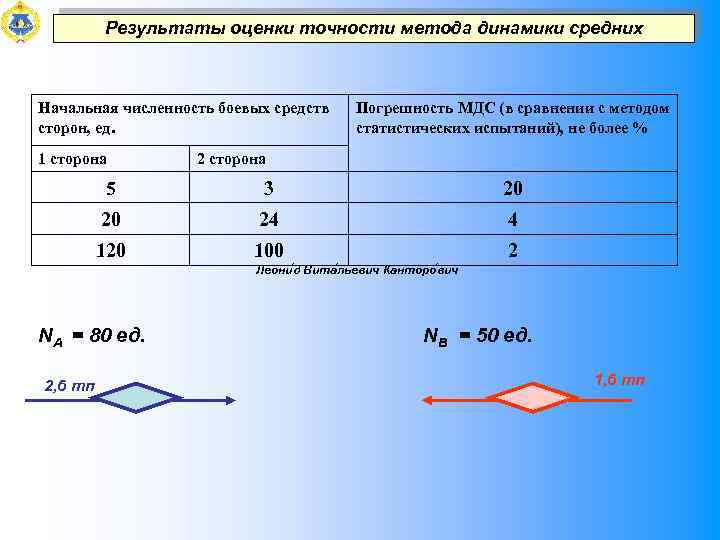Результаты оценки точности метода динамики средних Начальная численность боевых средств сторон, ед. 1 сторона Погрешность МДС (в сравнении с методом статистических испытаний), не более % 2 сторона 5 3 20 20 24 4 120 100 2 Леони д Вита льевич Канторо вич NА = 80 ед. NВ = 50 ед. 2, 6 тп 1, 6 тп

Курс: Исследование операций. Теория и практика моделирования Лекция №. Линейное программирование.

Леони д Вита льевич Канторо вич (6 (19) января 1912, Санкт-Петербург — 7 апреля 1986, Москва) — советский математик и экономист, пионер и один из создателей линейного программирования. 1934 году стал профессором (в 22 года), в 1935 году ему присвоена учёная степень доктора физико-математических наук без защиты диссертации. 1938 году Канторович женился на Наталье Ильиной, враче по профессии (у них родилось двое детей — сын и дочь). В 1938 году консультировал фанерный трест по проблеме эффективного использования лущильных станков. Канторович понял, что дело сводится к задаче максимизации линейной формы многих переменных при наличии большого числа ограничений в форме линейных равенств и неравенств. Он модифицировал метод разрешающих множителей Лагранжа для её решения и понял, что к такого рода задачам сводится колоссальное количество проблем экономики. Положил начало линейному программированию и его обобщениям (1939— 1940). В 1939 году опубликовал работу «Математические методы организации и планирования производства» , в которой описал задачи экономики, поддающиеся открытому им математическому методу и тем самым заложил основы линейного программирования. Лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов» (единственный советский ученый, удостоенный Нобелевской премии по экономике). Канторович — представитель петербургской математической школы П. Л. Чебышёва, ученик Г. М. Фихтенгольца и В. И. Смирнова. Канторович разделял и развивал взгляды П. Л. Чебышёва на математику как на единую дисциплину, все разделы которой взаимосвязаны, взаимозависимы и играют особую роль в развитии науки, техники, технологии и производства. Канторович выдвигал тезис взаимопроникновения математики и экономики и стремился к синтезу гуманитарных и точных технологий знания. Творчество Канторовича стало образцом научного служения, базирующегося на универсализации математического мышления.

Задача линейного программирования. Общая формулировка Целевая функция: Ограничения: Граничные условия: х2 ОДР Целевая функция х1

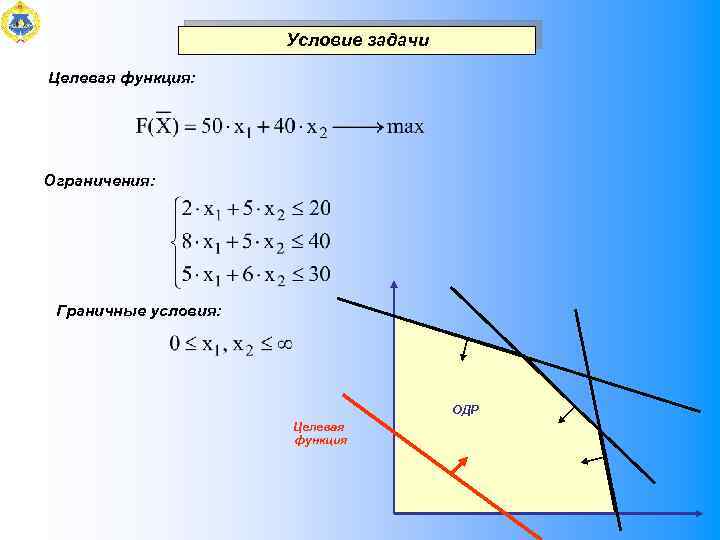Условие задачи Целевая функция: Ограничения: Граничные условия: ОДР Целевая функция

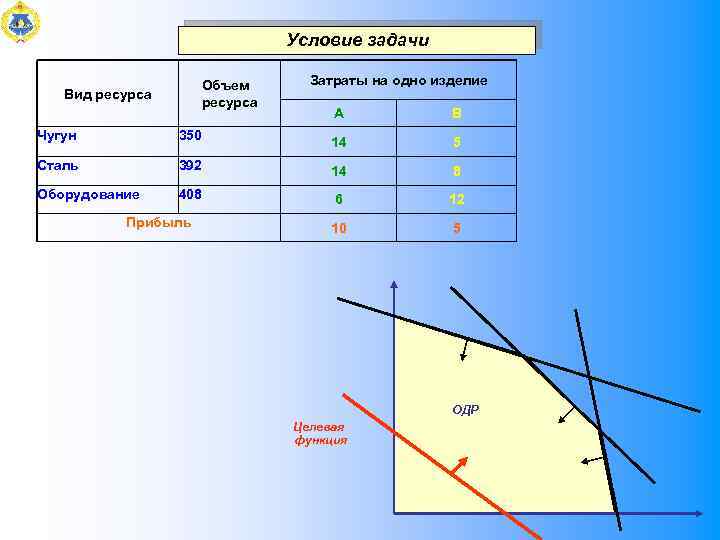Условие задачи Объем ресурса Вид ресурса Затраты на одно изделие А В Чугун 350 14 5 Сталь 392 14 8 Оборудование 408 6 12 10 5 Прибыль ОДР Целевая функция

Условие задачи 1 Компания производит полки для ванных комнат двух размеров А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 600 полок. Для каждой полки типа А требуется 4 м 2 материала, а для полки типа В 3 м 2 материала. Компания может получить до 1400 м 2 материала в неделю. Для изготовления одной полки типа А требуется 52 мин машинного времени, а для изготовления одной полки типа В — 130 мин. Станок можно использовать 280 ч в неделю. Если прибыль от продажи полок типа А составляет 4 усл. ед. , а от полок типа В 6 усл. ед. , то сколько полок каждого типа следует выпускать в неделю? Целевая функция: Ограничения: ОДР Целевая функция Граничные условия:

Условие задачи 2 Автозавод выпускает две модели: "Каприз" и (более дешевую) "Фиаско". На заводе работает 1500 неквалифицированных и 800 квалифицированных рабочих, каждому из которых оплачивается 40 ч в неделю. Для изготовления модели "Каприз" требуется 60 ч неквалифицированного и 30 ч квалифицированного труда; для "Фиаско" требуется 30 ч неквалифицированного и 10 ч квалифицированного труда. Каждая модель "Фиаско" требует затрат в размере 700 усл. ед. на сырье и комплектующие изделия, тогда как каждая модель "Каприз" требует затрат в размере 1500 усл. ед. Суммарные затраты не должны превосходить 700 000 усл. ед. в неделю. Рабочие, осуществляющие доставку, работают по пять дней в неделю и могут забрать с завода не более 200 машин в день. Каждая модель "Каприз" приносит фирме 800 усл. ед. прибыли, а каждая модель "Фиаско" 400 усл. ед. прибыли. Какой объем выпуска каждой модели Вы бы рекомендовали? Целевая функция: Ограничения: ОДР Целевая функция Граничные условия:

Условие задачи 3 Фабрика выпускает две модели тумбочек: «Обыкновенная» и «Резная» . Для изготовления модели «Обыкновенная» требуется 3 м 2 материала и 6 ч квалифицированного труда, для «Резной» требуется 5 м 2 и 8 ч 2. квалифицированного труда. Месячные запасы материала 150 м 2. Рабочий квалифицированного труда. Месячные запасы материала 150 м Рабочий месяц – 240 ч. Кроме того арендуется в месяц 120 ч работы обрабатывающего месяц – 240 ч. Кроме того арендуется в месяц 120 ч работы обрабатывающего центра. Для изготовления модели «Обыкновенная» требуется 2 ч работы центра, для «Резной» - 4 ч работы. Модель «Обыкновенная» приносит 10 усл. ед. прибыли, а модель «Резная» 30 усл. ед. прибыли. Какой объем выпуска каждой модели Вы бы по рекомендовали? Целевая функция: Ограничения: ОДР Граничные условия: Целевая функция

Курс: Исследование операций. Теория и практика моделирования Лекция №. Линейное программирование. Транспортная задача

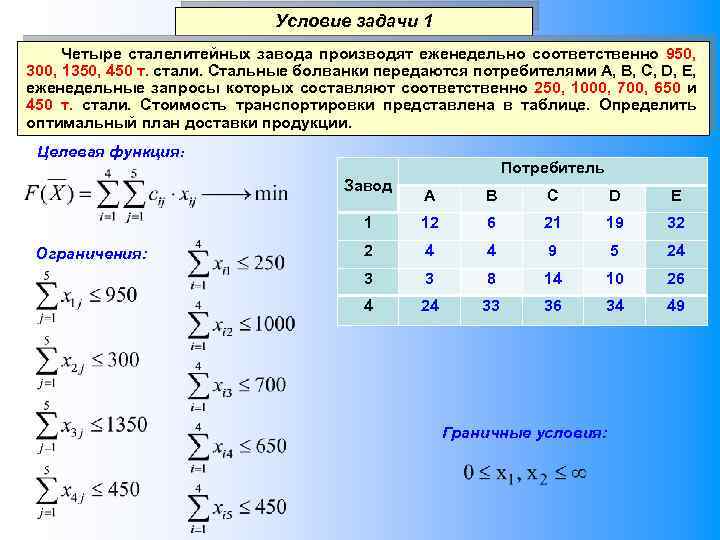Условие задачи 1 Четыре сталелитейных завода производят еженедельно соответственно 950, 300, 1350, 450 т. стали. Стальные болванки передаются потребителями A, B, C, D, E, еженедельные запросы которых составляют соответственно 250, 1000, 700, 650 и 450 т. стали. Стоимость транспортировки представлена в таблице. Определить оптимальный план доставки продукции. Целевая функция: Потребитель Завод B C D E 1 Ограничения: A 12 6 21 19 32 2 4 4 9 5 24 3 3 8 14 10 26 4 24 33 36 34 49 Граничные условия:

НИЦ систем управления ВВС 30 ЦНИИ МО РФ Курс: Исследование операций. Теория и практика моделирования Лекция 2. Теория игр. Классификация игр. Игры в условиях неопределенности и с вероятностно заданной информацией Ревин С. А. , главный научный сотрудник, кандидат технических наук, доцент

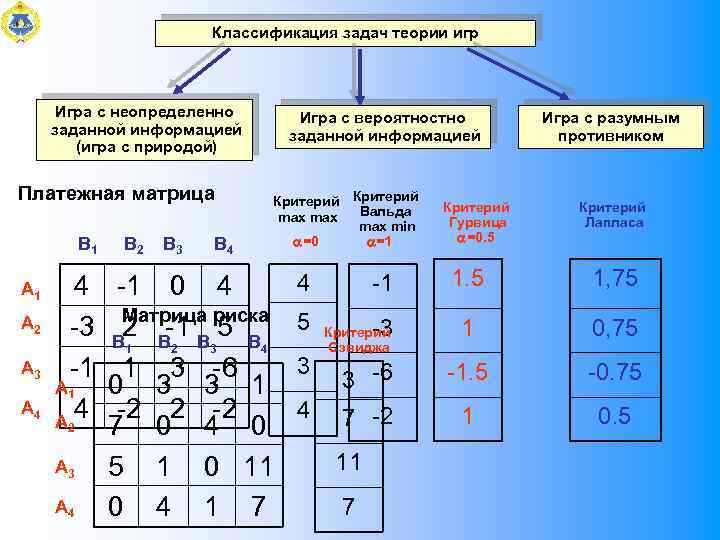Классификация задач теории игр Игра с неопределенно заданной информацией (игра с природой) Платежная матрица B 1 А 2 А 3 А 4 4 -3 -1 А 1 4 А 2 А 3 А 4 B 2 B 3 B 4 Игра с вероятностно заданной информацией Критерий Вальда max max min =0 =1 -1 0 4 Матрица риска 2 -1 5 B B 1 B 2 B 3 4 1 3 -6 0 3 3 1 -2 2 -2 7 0 4 0 5 1 0 11 0 4 1 7 3 4 Критерий Лапласа -1 1. 5 1, 75 -3 1 0, 75 3 -6 -1. 5 -0. 75 7 -2 1 0. 5 4 5 Критерий Гурвица =0. 5 Игра с разумным противником Критерий Сэвиджа 11 7

Задачи теории игр У компании А существует 4 варианта инвестирования средств в различные отрасли. На рынке возможна одна из 4 ситуаций (В 1, В 2, В 3 и В 4) которая может привести к получению прибыли или убытков (в млн. руб). Для известной платежной матрицы обосновать решения исходя из критериев Гурвица, Сэвиджа и Лапласа. Для критерия Гурвица принять значение коэффициента риска 0, 4. Платежная матрица B 1 B 2 B 3 B 4 А 1 12 -5 -2 -3 А 2 -4 -6 7 -1 А 3 2 14 -3 -14 А 4 -2 0 -9 12 Как изменится решение, если появится информация о возможных вероятностях появления ситуаций В 1, В 2, В 3 и В 4 0, 4, 0, 1 и 0, 4 соответственно?

Задачи теории игр Компания, специализирующаяся на программных разработках, планирует принять участие в тендере на получение госзаказа на разработку информационной системы. Тендер проводится закрытым способом, т. е. предложения подаются участниками в запечатанных конвертах и неизвестны другим участникам. По оценкам компании, участие в тендере обойдется в 5 000 руб. , а выполнение заказа в 95 000 руб. Из опыта предыдущих тендеров известно, что с вероятностью 30% конкуренции вообще не будет. Кроме того, известно, что цена подобного тендера имеет условные вероятности представленные в таблице. Необходимо принять решение, участвовать ли в аукционе и, если да, то с какой ценой. Необходимо выбрать решение, которое максимизирует ожидаемую прибыль. Цена тендера Вероятность Менее 115 000 0, 2 От 115 000 до 120 000 0, 4 От 120 000 до 125 000 0, 3 Более 125 00 Платежная матрица: 0, 1 Как изменится решение, если перед подачей заявки станет известно, что одна из фирм конкурентов участвует в тендере?

НИЦ систем управления ВВС 30 ЦНИИ МО РФ Курс: Исследование операций. Теория и практика моделирования Лекция 3. Теория игр. Игры в условиях неопределенности и с вероятностно заданной информацией Ревин С. А. , главный научный сотрудник, кандидат технических наук, доцент

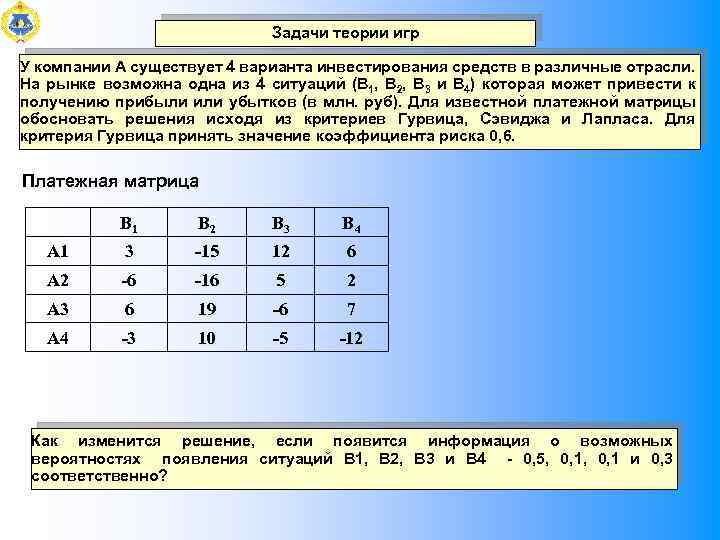Задачи теории игр У компании А существует 4 варианта инвестирования средств в различные отрасли. На рынке возможна одна из 4 ситуаций (В 1, В 2, В 3 и В 4) которая может привести к получению прибыли или убытков (в млн. руб). Для известной платежной матрицы обосновать решения исходя из критериев Гурвица, Сэвиджа и Лапласа. Для критерия Гурвица принять значение коэффициента риска 0, 6. Платежная матрица B 1 B 2 B 3 B 4 А 1 3 -15 12 6 А 2 -6 -16 5 2 А 3 6 19 -6 7 А 4 -3 10 -5 -12 Как изменится решение, если появится информация о возможных вероятностях появления ситуаций В 1, В 2, В 3 и В 4 0, 5, 0, 1 и 0, 3 соответственно?

Задачи теории игр Компания, специализирующаяся на программных разработках, планирует принять участие в тендере на получение госзаказа на разработку информационной системы. Тендер проводится закрытым способом, т. е. предложения подаются участниками в запечатанных конвертах и неизвестны другим участникам. По оценкам компании, участие в тендере обойдется в 5 000 руб. , а выполнение заказа в 50 000 руб. Из опыта предыдущих тендеров известно, что с вероятностью 40% конкуренции вообще не будет. Кроме того, известно, что цена подобного тендера имеет условные вероятности представленные в таблице. Необходимо принять решение, участвовать ли в аукционе и, если да, то с какой ценой. Необходимо выбрать решение, которое максимизирует ожидаемую прибыль. Цена тендера Вероятность Менее 70 000 0, 2 От 70 000 до 80 000 0, 3 От 80 000 до 90 000 0, 4 Более 90 00 Платежная матрица: 0, 1 Как изменится решение, если перед подачей заявки станет известно, что одна из фирм конкурентов участвует в тендере?

Дерево решений Р=0, 3 115 – 95 -5 =15 НЕТ 0, 3 Есть конкуренты? 0 НЕТ 115 Участвовать в тендере? НЕТ 0, 2 -5 Выигран тендер? ДА 0, 7 ДА 0, 8 ДА - 5 120 НЕТ 0, 3 Есть конкуренты? 125 НЕТ 0, 3 Есть конкуренты? ДА Р=0, 3 125 – 95 -5 =25 ДА Р=0, 7*0, 8=0, 563 115 – 95 -5 =15 Р=0, 3 120 – 95 -5 =20 НЕТ 0, 4 -5 Выигран тендер? 0, 7 НЕТ 0, 9 -5 Выигран тендер? 0, 7 ДА 0, 1 Р=0, 7*0, 1=0, 07 125– 95 -5 =25 ДА 0, 6 Р=0, 7*0, 4=0, 28 120 – 95 -5 =20

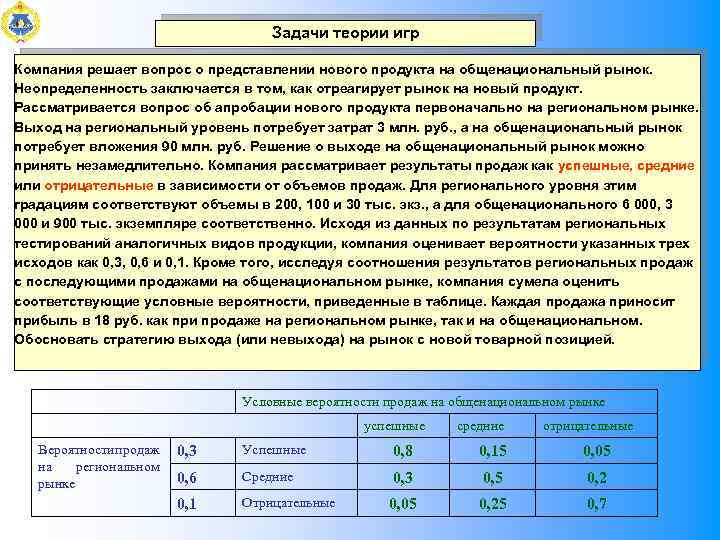Задачи теории игр Компания решает вопрос о представлении нового продукта на общенациональный рынок. Неопределенность заключается в том, как отреагирует рынок на новый продукт. Рассматривается вопрос об апробации нового продукта первоначально на региональном рынке. Выход на региональный уровень потребует затрат 3 млн. руб. , а на общенациональный рынок потребует вложения 90 млн. руб. Решение о выходе на общенациональный рынок можно принять незамедлительно. Компания рассматривает результаты продаж как успешные, средние или отрицательные в зависимости от объемов продаж. Для регионального уровня этим градациям соответствуют объемы в 200, 100 и 30 тыс. экз. , а для общенационального 6 000, 3 000 и 900 тыс. экземпляре соответственно. Исходя из данных по результатам региональных тестирований аналогичных видов продукции, компания оценивает вероятности указанных трех исходов как 0, 3, 0, 6 и 0, 1. Кроме того, исследуя соотношения результатов региональных продаж с последующими продажами на общенациональном рынке, компания сумела оценить соответствующие условные вероятности, приведенные в таблице. Каждая продажа приносит прибыль в 18 руб. как при продаже на региональном рынке, так и на общенациональном. Обосновать стратегию выхода (или невыхода) на рынок с новой товарной позицией. Условные вероятности продаж на общенациональном рынке успешные Вероятностипродаж на региональном рынке средние отрицательные 0, 3 Успешные 0, 8 0, 15 0, 05 0, 6 Средние 0, 3 0, 5 0, 2 0, 1 Отрицательные 0, 05 0, 25 0, 7

Курс: Исследование операций. Теория и практика моделирования Лекция 4. Теория игр. Игра с разумным противником

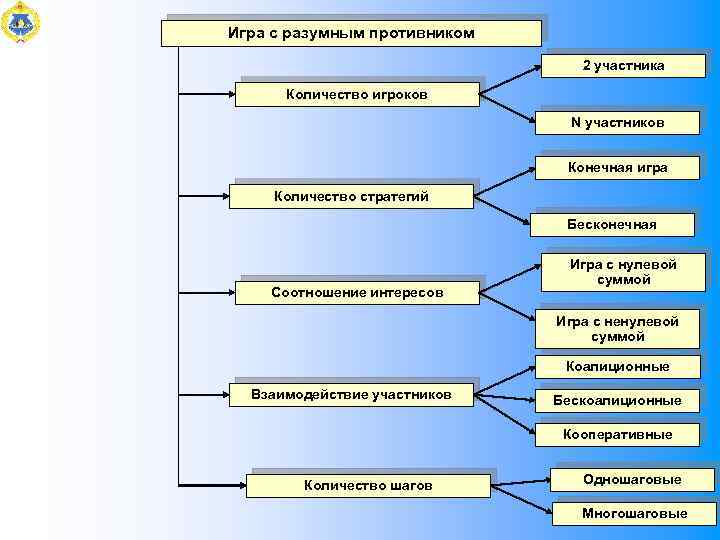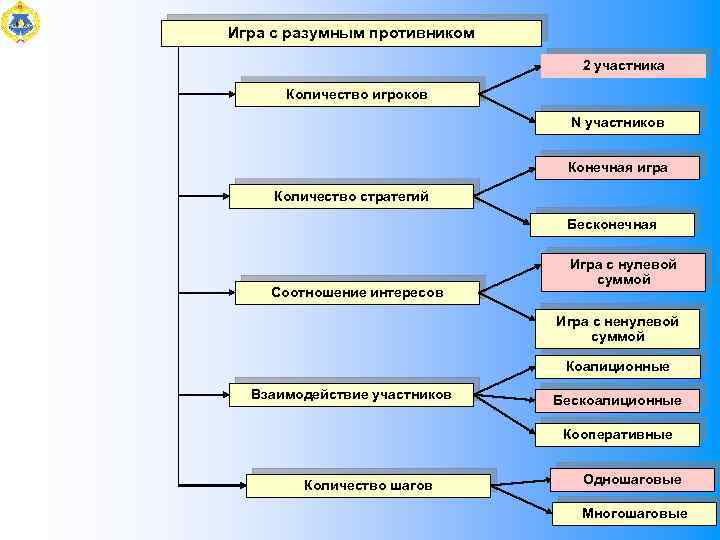Игра с разумным противником 2 участника Количество игроков N участников Конечная игра Количество стратегий Бесконечная Соотношение интересов Игра с нулевой суммой Игра с ненулевой суммой Коалиционные Взаимодействие участников Бескоалиционные Кооперативные Количество шагов Одношаговые Многошаговые

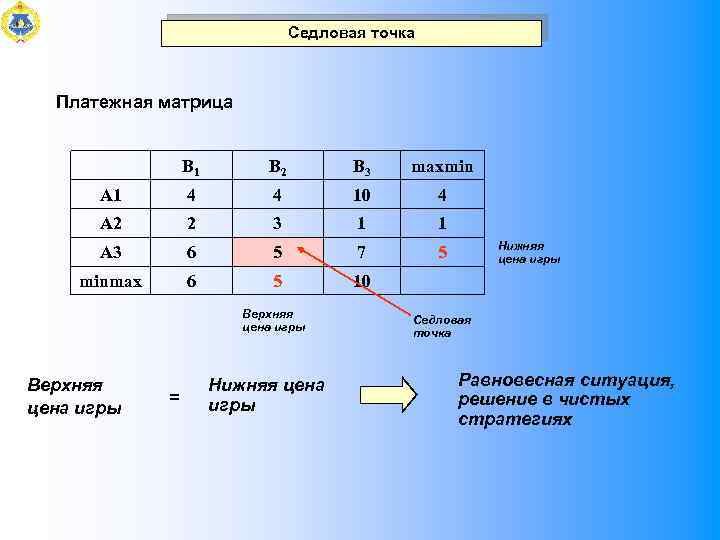Седловая точка Платежная матрица B 1 B 2 B 3 maxmin А 1 4 4 10 4 А 2 2 3 1 1 А 3 6 5 7 5 minmax 6 5 10 Верхняя цена игры = Нижняя цена игры Седловая точка Равновесная ситуация, решение в чистых стратегиях

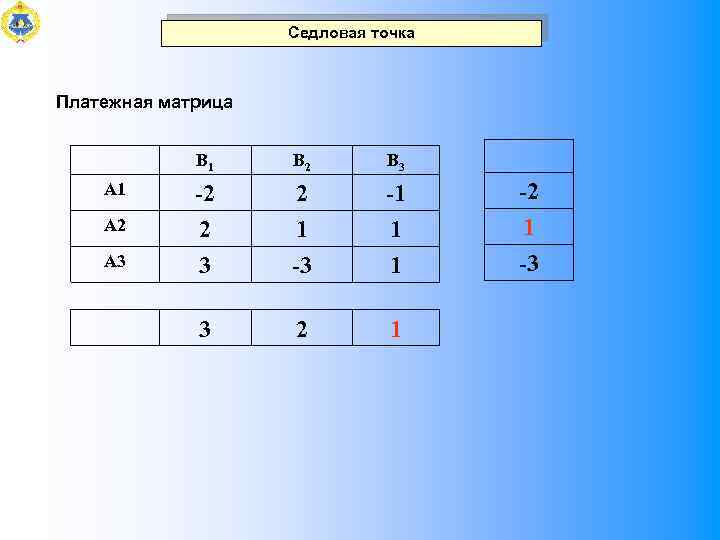Седловая точка Платежная матрица B 1 А 2 А 3 B 2 B 3 -2 2 3 2 1 -3 -1 1 1 3 2 1 -3

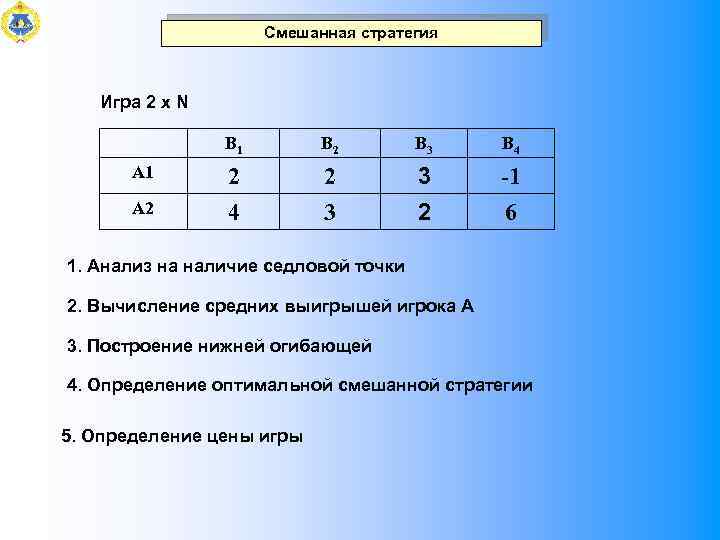Смешанная стратегия Игра 2 х N B 1 А 2 B 3 B 4 2 3 3 2 -1 6 1. Анализ на наличие седловой точки 2. Вычисление средних выигрышей игрока А 3. Построение нижней огибающей 4. Определение оптимальной смешанной стратегии 5. Определение цены игры

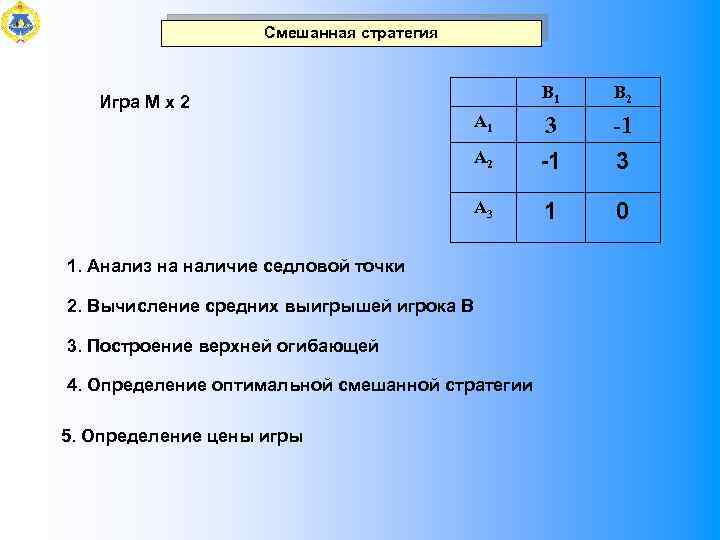Смешанная стратегия B 1 B 2 А 1 3 -1 А 2 1 3 А 3 Игра М х 2 1 0 1. Анализ на наличие седловой точки 2. Вычисление средних выигрышей игрока В 3. Построение верхней огибающей 4. Определение оптимальной смешанной стратегии 5. Определение цены игры

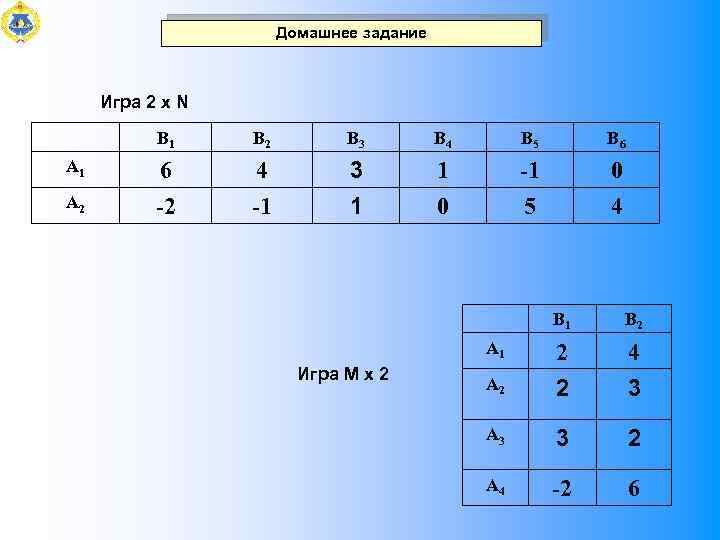Домашнее задание Игра 2 х N B 1 А 2 B 3 B 4 B 5 B 6 6 -2 4 -1 3 1 1 0 -1 5 0 4 B 1 А 1 Игра М х 2 B 2 2 4 А 2 2 3 А 3 3 2 А 4 -2 6

НИЦ систем управления ВВС ЦНИИ авиационной и космической техники Курс: Исследование операций. Теория и практика моделирования Лекция 5. Аппроксимация зависимостей линейными функциями. Метод наименьших квадратов. Парная и множественная линейные регрессии. Лекция 6. Нелинейная регрессия. Численное нахождение коэффициентов аппроксимирующих функций Ревин С. А. , главный научный сотрудник, кандидат технических наук, доцент

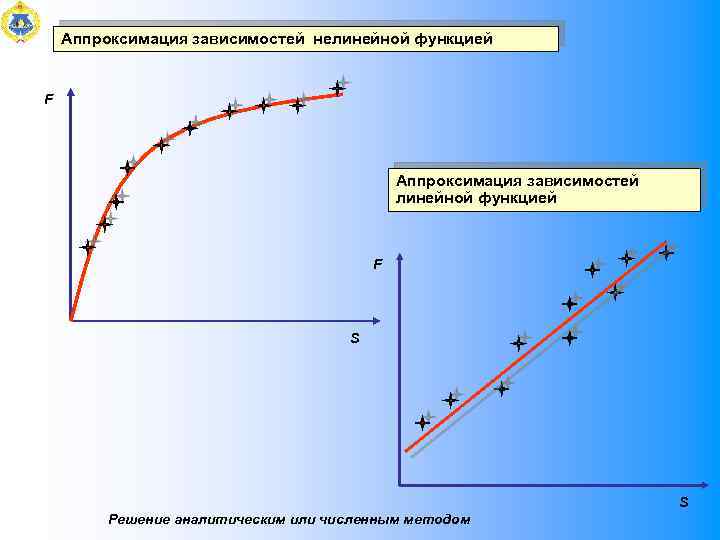Аппроксимация зависимостей нелинейной функцией F Аппроксимация зависимостей линейной функцией F S S Решение аналитическим или численным методом

Определение коэффициентов аппроксимирующей функции численным методом // Ввод исходных данных Min = 1 0000; For (a = 0; a=k+0. 1; a<=4) { For (k = 2. 2; k=k+0. 01; k<=3. 2) { sum=0; For (i=1; i++; i<=N) Sum=sum + (Y(i) – (a+k*sqr( X(i)))) ^2 If (sum <= min) { min = sum; amin = a; kmin = k; } } // Вывод результата (коэфф. аппроксимирующей функции)

Курс: Исследование операций. Теория и практика моделирования Лекция 6. Моделирование операций по схеме марковских случайных операций. Марковские процессы с дискретным состоянием и дискретным временем Лекция 7. Моделирование операций по схеме марковских случайных операций. Марковские процессы с дискретным состоянием и непрерывным временем

Марковские процессы Андре й Андре евич Ма рков (2 (14) июня 1856, Рязань — 20 июля 1922, Петроград) — русский математик, академик, ученик П. Л. Чебышева. А. А. Марков является первооткрывателем обширного класса стохастических процессов с дискретной и непрерывной временной компонентой, названных его именем. Марковские процессы обладают следующим (марковским) свойством: следующее состояние процесса зависит, вероятностно, только от текущего состояния. В то время, когда эта теория была построена, она считалась весьма абстрактной, однако в настоящее время практические применения данной теории чрезвычайно многочисленны. Теория цепей Маркова выросла в огромную и весьма важную область научных исследований — теорию марковских случайных процессов, которая в свою очередь представляет основу общей теории стохастических процессов А. А. Марков существенно продвинул классические исследования предшественников, касающиеся закона больших чисел и центральной предельной теоремы теории вероятностей, а также распространил их и на цепи Маркова. Следует указать, что А. А. Марков своим открытием (как и затем А. Н. Колмогоров, предложивший строгую теоретико-вероятностную формулировку на основе теории меры) сделал крупнейший вклад в теорию случайных процессов и теорию вероятностей вообще.

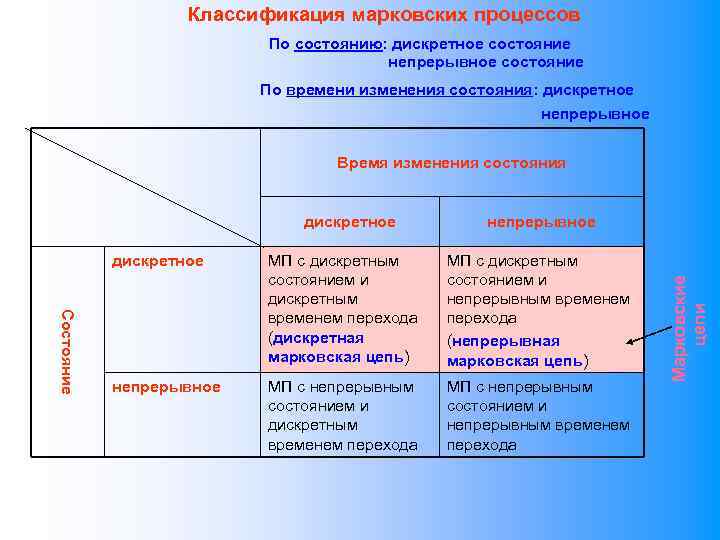Классификация марковских процессов По состоянию: дискретное состояние непрерывное состояние По времени изменения состояния: дискретное непрерывное Время изменения состояния непрерывное Состояние дискретное МП с дискретным состоянием и дискретным временем перехода (дискретная марковская цепь) МП с дискретным состоянием и непрерывным временем перехода (непрерывная марковская цепь) непрерывное МП с непрерывным состоянием и дискретным временем перехода МП с непрерывным состоянием и непрерывным временем перехода Марковские цепи дискретное

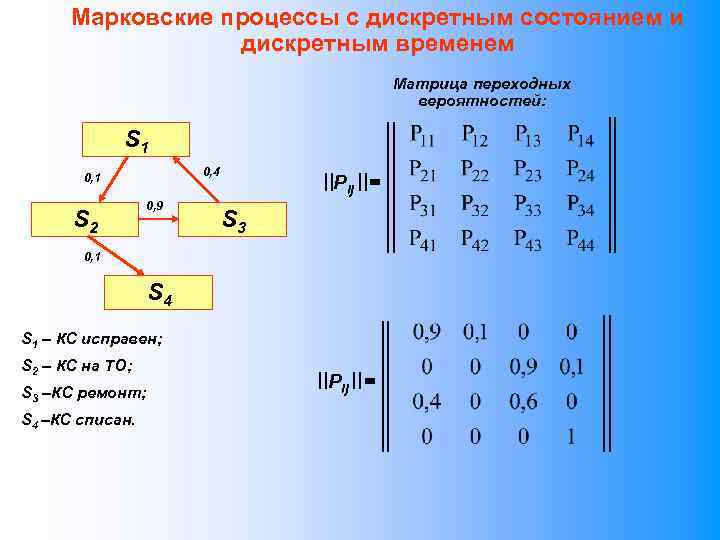Марковские процессы с дискретным состоянием и дискретным временем Матрица переходных вероятностей: S 1 0, 4 0, 1 S 2 0, 9 Pij = S 3 0, 1 S 4 S 1 – КС исправен; S 2 – КС на ТО; S 3 –КС ремонт; S 4 –КС списан. Pij =

Марковские процессы с дискретным состоянием и дискретным временем S 0 0, 1 S 1 0, 3 Рисунок 0, 1 0, 3 S 2 0, 8 S 3 0, 4 S 0 – самолет не поврежден; S 1 – средние повреждения; S 2 – существенные повреждения; S 3 – сбит. Pij =

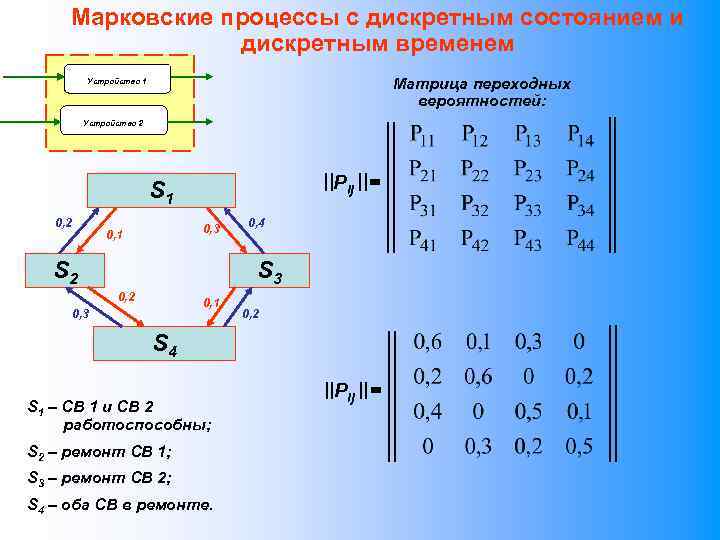Марковские процессы с дискретным состоянием и дискретным временем Матрица переходных вероятностей: Устройство 1 Устройство 2 Pij = S 1 0, 2 0, 3 0, 1 S 2 0, 4 S 3 0, 2 0, 1 0, 3 0, 2 S 4 S 1 – СВ 1 и СВ 2 работоспособны; S 2 – ремонт СВ 1; S 3 – ремонт СВ 2; S 4 – оба СВ в ремонте. Pij =

Андре й Никола евич Колмого ров (урождённый Катаев, 12 (25) апреля 1903, Тамбов — 20 октября 1987, Москва) — советский математик, один из крупнейших математиков ХХ века. В сентябре 1942 года Колмогоров женится на своей однокласснице по гимназии Анне Дмитриевне Егоровой, дочери известного историка, профессора, члена-корреспондента Академии наук Дмитрия Николаевича Егорова. Их брак продолжался 45 лет. Собственных детей у Колмогорова не было. В последние годы Колмогоров заведовал кафедрой математической логики в МГУ и преподавал в ФМШ № 18 при МГУ (ныне — СУНЦ МГУ имени А. Н Колмогорова). Круг жизненных интересов Колмогорова не замыкался чистой математикой: его увлекали и философские проблемы, и история науки, и живопись, и литература, и музыка. По меткому выражению Стефана Банаха: «Математик — это тот, кто умеет находить аналогии между утверждениями. Лучший математик — кто устанавливает аналогии доказательств. Более сильный может заметить аналогии теорий. Но есть и такие, кто между аналогиями видит аналогии» . К этим редким представителям последних относится и Андрей Николаевич Колмогоров — один из крупнейших математиков двадцатого века. Колмогоров скончался 20 октября 1987 г в Москве. Похоронен на Новодевичьем кладбище

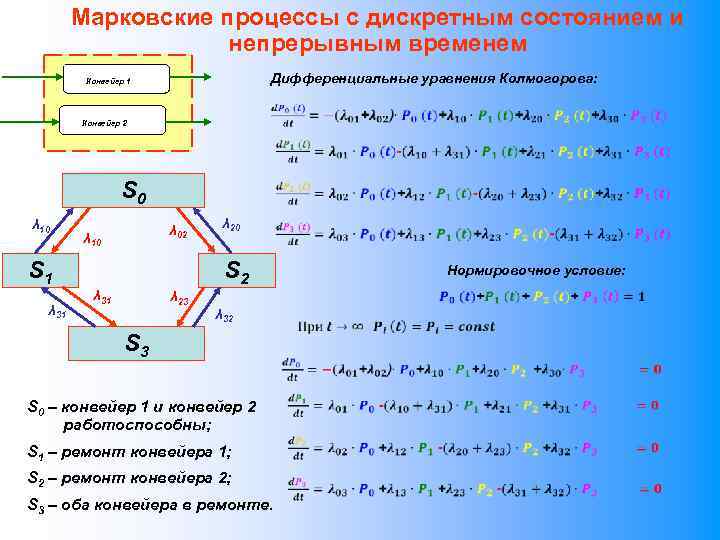Марковские процессы с дискретным состоянием и непрерывным временем Дифференциальные уравнения Колмогорова: Конвейер 1 Конвейер 2 S 0 λ 10 λ 02 λ 10 S 1 λ 31 λ 20 S 2 λ 31 λ 23 Нормировочное условие: λ 32 S 3 S 0 – конвейер 1 и конвейер 2 работоспособны; S 1 – ремонт конвейера 1; S 2 – ремонт конвейера 2; S 3 – оба конвейера в ремонте.

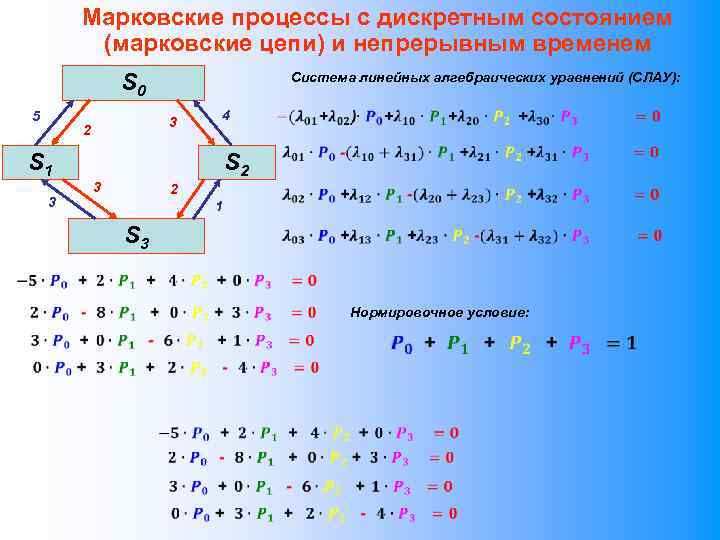Марковские процессы с дискретным состоянием (марковские цепи) и непрерывным временем S 0 5 Система линейных алгебраических уравнений (СЛАУ): 3 2 4 S 1 3 S 2 3 2 1 S 3 Нормировочное условие:

Межотраслевой баланс Васи лий Васи льевич Лео нтьев (5 августа 1905, Мюнхен[2] — 5 февраля 1999, Нью-Йорк) — американский экономист российского происхождения, создатель теории межотраслевого анализа, лауреат Нобелевской премии по экономике за 1973 год «за развитие метода „затраты — выпуск“ и за его применение к важным экономическим проблемам» . В 1925 году завершил изучение философии и социологии в Ленинградском университете. Позже Леонтьев изучал экономические науки в Берлине и за диссертацию «Круговорот экономики» получил докторскую степень. После начала Второй мировой войны работал консультантом по экономическому планированию для военно-воздушных сил США. Под его руководством была построена матрица «затратывыпуск» для экономики Германии. Матрица служила основой для выбора целей ВВС Леонтьев разработал анализ «затраты-выпуск» , за что в 1973 получил Нобелевскую премию. В честь Леонтьева назван ряд экономических явлений — например, модель Леонтьева и парадокс Леонтьева. Межотраслевой баланс (МОБ, метод «затраты-выпуск» ) — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевой баланс составляется в денежной и натуральной формах. Увлекался парусным спортом и, когда объяснял студентам, как функционирует экономика страны, сравнивал её с яхтой в море. Чтобы дела шли хорошо, нужен ветер, — это заинтересованность. Руль — государственное регулирование.

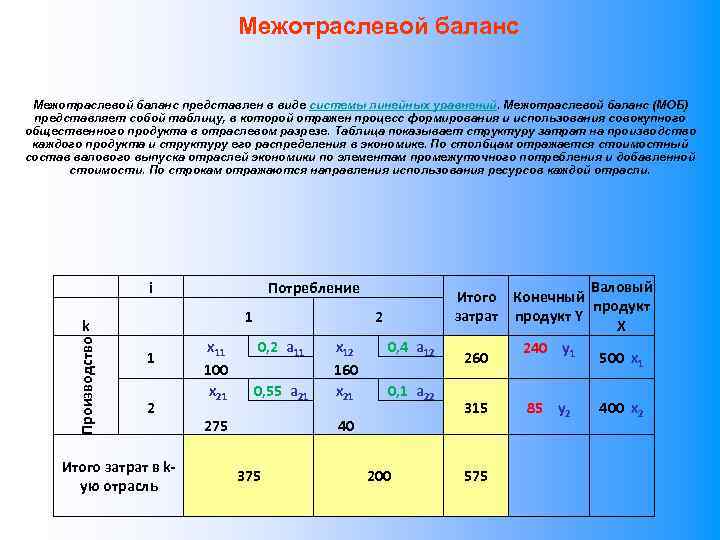Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли. i Производство k Потребление 1 1 2 Итого затрат в kую отрасль 2 x 11 100 x 21 0, 2 a 11 0, 55 a 21 x 12 160 x 21 275 40 375 0, 4 a 12 0, 1 a 22 200 Валовый Итого Конечный продукт затрат продукт Y Х 240 y 1 260 500 x 1 315 85 y 2 400 x 2 575

Поиск решения (Excel)

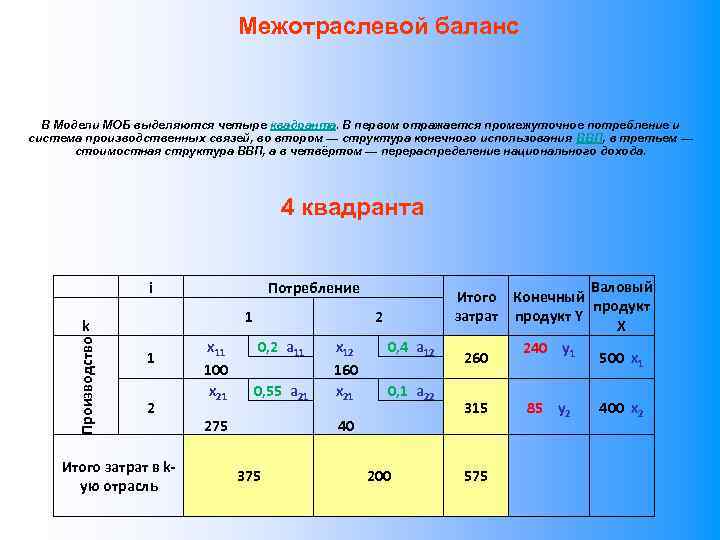Межотраслевой баланс В Модели МОБ выделяются четыре квадранта. В первом отражается промежуточное потребление и система производственных связей, во втором — структура конечного использования ВВП, в третьем — стоимостная структура ВВП, а в четвёртом — перераспределение национального дохода. 4 квадранта i Производство k Потребление 1 1 2 Итого затрат в kую отрасль 2 x 11 100 x 21 0, 2 a 11 0, 55 a 21 x 12 160 x 21 275 40 375 0, 4 a 12 0, 1 a 22 200 Валовый Итого Конечный продукт затрат продукт Y Х 240 y 1 260 500 x 1 315 85 y 2 400 x 2 575

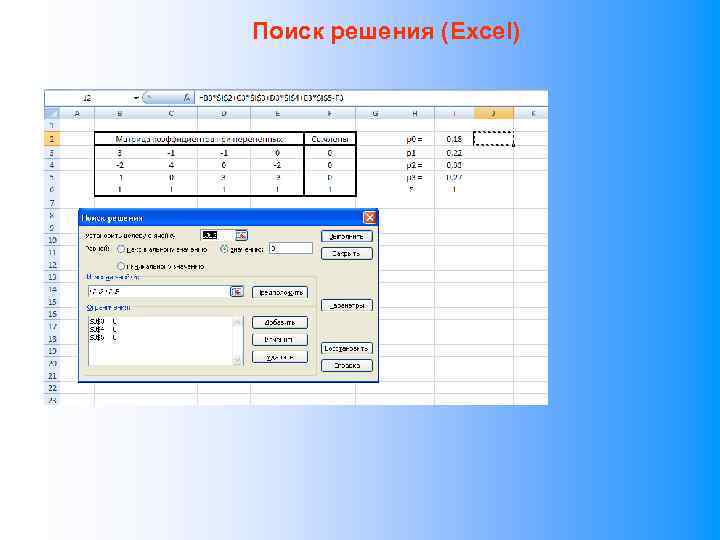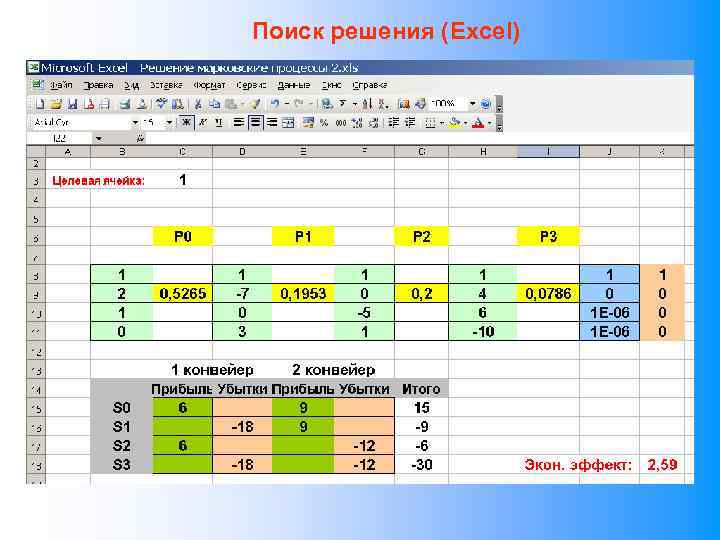Поиск решения (Excel)

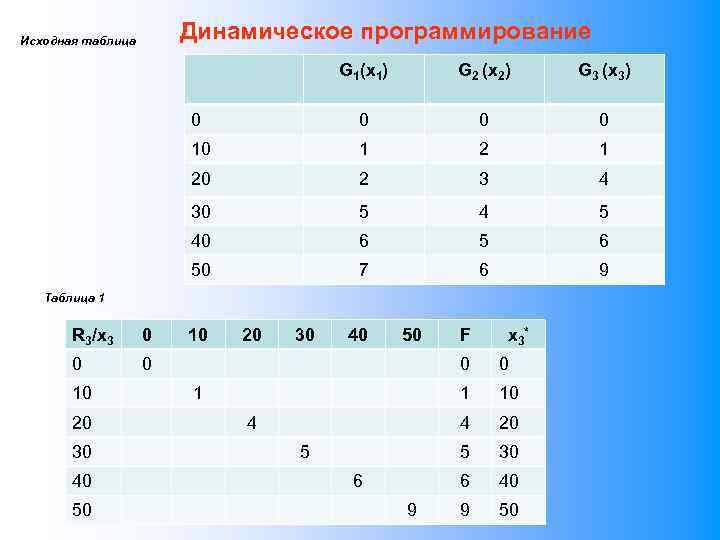Динамическое программирование Исходная таблица G 1(x 1) G 2 (x 2) G 3 (x 3) 0 0 10 1 20 2 3 4 30 5 40 6 50 7 6 9 Таблица 1 R 3/x 3 0 0 0 10 20 30 40 50 F x 3 * 0 1 6 9 30 6 5 20 5 4 10 4 1 0 40 9 50

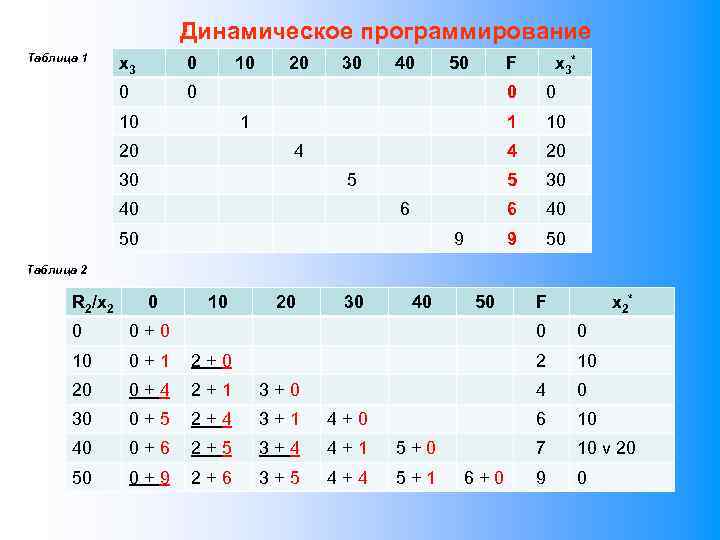Динамическое программирование Таблица 1 x 3 0 0 10 20 30 40 50 F 0 x 3 * 0 10 1 20 30 40 50 9 40 9 6 30 6 5 20 5 4 10 4 1 0 50 Таблица 2 R 2/x 2 0 10 20 30 40 0 0+0 10 0+1 2+0 20 0+4 2+1 3+0 30 0+5 2+4 3+1 4+0 40 0+6 2+5 3+4 4+1 5+0 50 0+9 2+6 3+5 4+4 5+1 50 F x 2 * 0 2 10 4 0 6 10 7 6+0 0 10 v 20 9 0

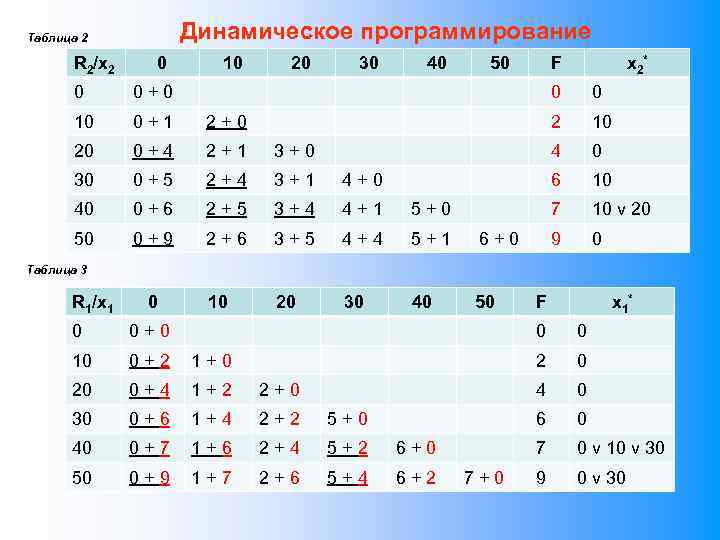Динамическое программирование Таблица 2 R 2/x 2 0 10 20 30 40 50 0 0+0 10 0+1 2+0 20 0+4 2+1 3+0 30 0+5 2+4 3+1 4+0 40 0+6 2+5 3+4 4+1 5+0 50 0+9 2+6 3+5 4+4 5+1 6+0 10 20 30 40 50 F x 2 * 0 0 2 10 4 0 6 10 7 10 v 20 9 0 Таблица 3 R 1/x 1 0 0 0+0 10 0+2 1+0 20 0+4 1+2 2+0 30 0+6 1+4 2+2 5+0 40 0+7 1+6 2+4 5+2 6+0 50 0+9 1+7 2+6 5+4 6+2 F x 1 * 0 2 0 4 0 6 0 7 7+0 0 0 v 10 v 30 9 0 v 30

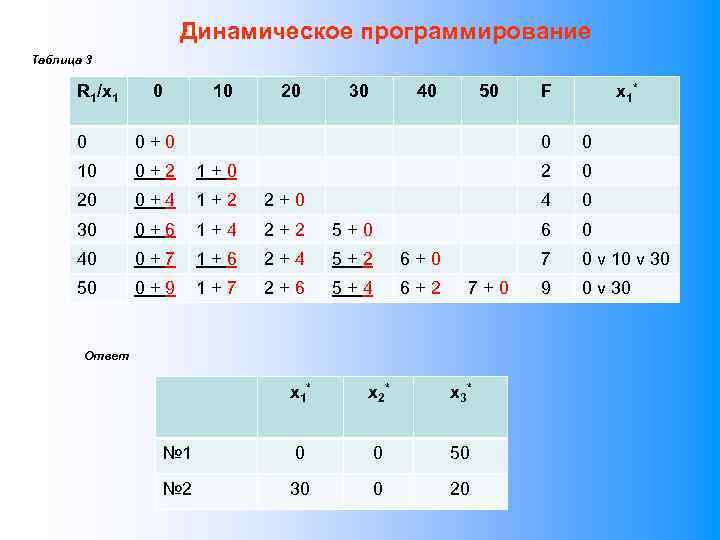Динамическое программирование Таблица 3 R 1/x 1 0 10 20 30 40 0 0+0 10 0+2 1+0 20 0+4 1+2 2+0 30 0+6 1+4 2+2 5+0 40 0+7 1+6 2+4 5+2 6+0 50 0+9 1+7 2+6 5+4 6+2 50 F x 1 * 0 2 x 2 * x 3 * № 1 0 0 50 № 2 30 0 20 0 7 x 1 * 0 6 Ответ 0 4 7+0 0 0 v 10 v 30 9 0 v 30

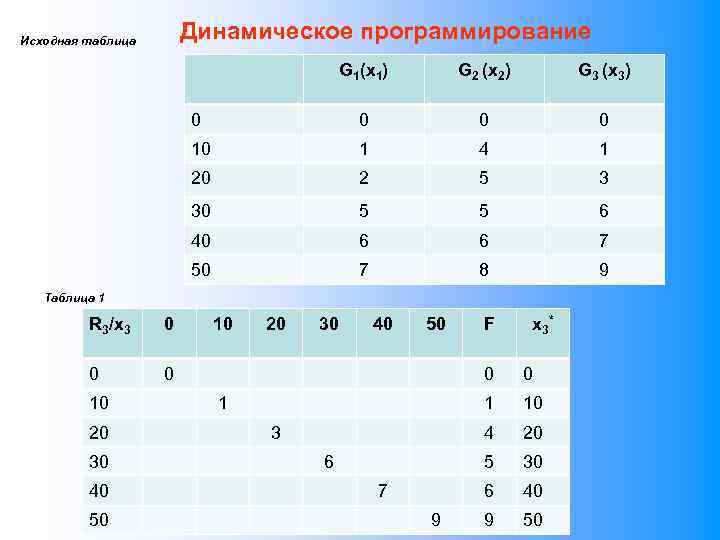Динамическое программирование Исходная таблица G 1(x 1) G 2 (x 2) G 3 (x 3) 0 0 10 1 4 1 20 2 5 3 30 5 5 6 40 6 6 7 50 7 8 9 Таблица 1 R 3/x 3 0 0 0 10 20 30 40 50 F x 3 * 0 1 7 9 30 6 6 20 5 3 10 4 1 0 40 9 50

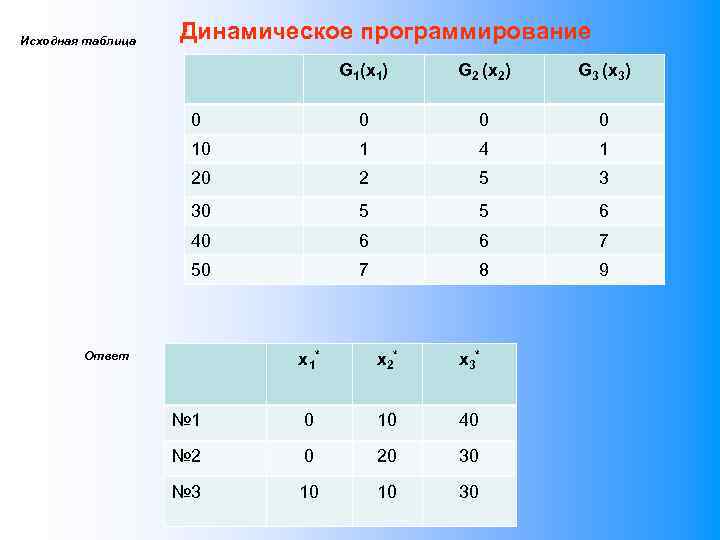Исходная таблица Динамическое программирование G 1(x 1) G 2 (x 2) G 3 (x 3) 0 0 10 1 4 1 20 2 5 3 30 5 5 6 40 6 6 7 50 7 8 9 x 1 * x 2 * x 3 * № 1 0 10 40 № 2 0 20 30 № 3 10 10 30 Ответ