КУРС ФИЗИКИ ВВЕДЕНИЕ Физика наука изучающая

КУРС ФИЗИКИ. ВВЕДЕНИЕ • Физика – наука, изучающая законы движения и взаимодействия материальных тел и полей. • Курс физики принято разделять на 3 раздела: • часть 1. Механика и молекулярная физика • часть 2. Электромагнетизм и волны • часть 3. Квантовая физика В курсе физики изучаются физические законы – общие закономерности, которым подчиняются физические процессы. Эти процессы изучаются, как правило, в специальных условиях физического эксперимента, в ходе которого происходит измерение физических величин, характеризующих свойства тел или явление. Мир пространства и времени, в котором мы живем характеризуется фундаментальными величинами – длиной (мерой протяженности тел) и временем (мерой продолжительности процесса). Для описания движения тела в физике выбирается система отсчета – система координат, связанная с некоторым телом Диапазон расстояний и интервалов времени во Вселенной представлены на следующих таблицах.

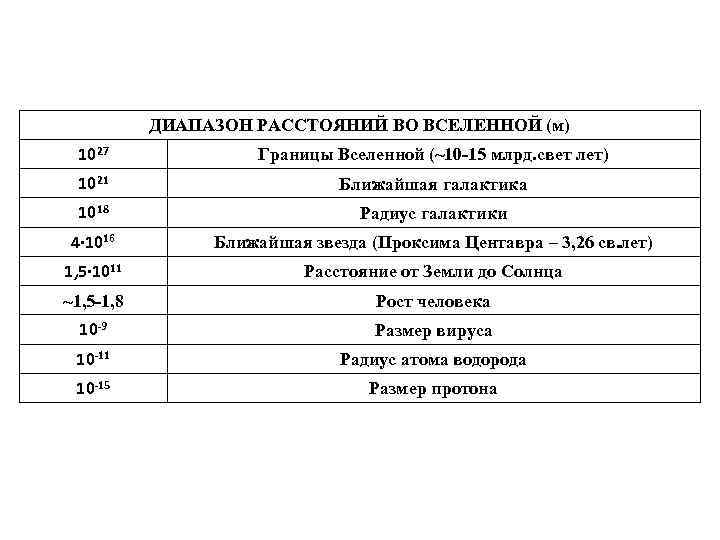ДИАПАЗОН РАССТОЯНИЙ ВО ВСЕЛЕННОЙ (м) 1027 Границы Вселенной (~10 -15 млрд. свет лет) 1021 Ближайшая галактика 1018 Радиус галактики 4· 1016 Ближайшая звезда (Проксима Центавра – 3, 26 св. лет) 1, 5· 1011 Расстояние от Земли до Солнца ~1, 5 -1, 8 Рост человека 10 -9 Размер вируса 10 -11 Радиус атома водорода 10 -15 Размер протона

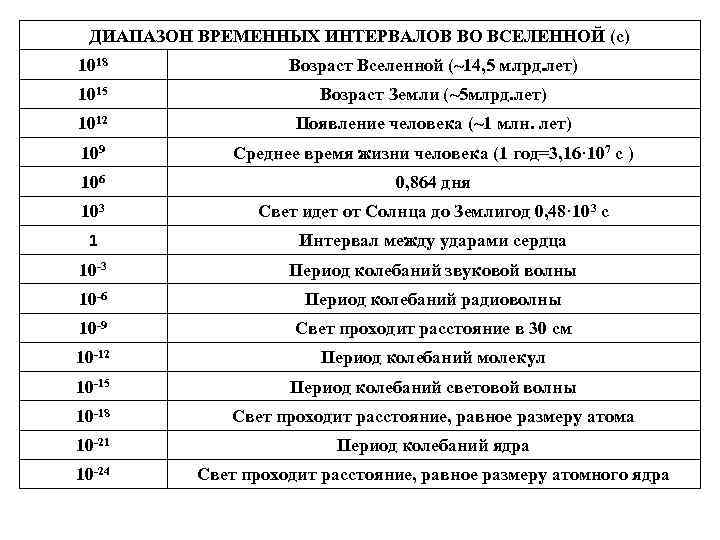ДИАПАЗОН ВРЕМЕННЫХ ИНТЕРВАЛОВ ВО ВСЕЛЕННОЙ (с) 1018 Возраст Вселенной (~14, 5 млрд. лет) 1015 Возраст Земли (~5 млрд. лет) 1012 Появление человека (~1 млн. лет) 109 Среднее время жизни человека (1 год=3, 16· 107 с ) 106 0, 864 дня 103 Свет идет от Солнца до Землигод 0, 48· 103 с 1 Интервал между ударами сердца 10 -3 Период колебаний звуковой волны 10 -6 Период колебаний радиоволны 10 -9 Свет проходит расстояние в 30 см 10 -12 Период колебаний молекул 10 -15 Период колебаний световой волны 10 -18 Свет проходит расстояние, равное размеру атома 10 -21 Период колебаний ядра 10 -24 Свет проходит расстояние, равное размеру атомного ядра

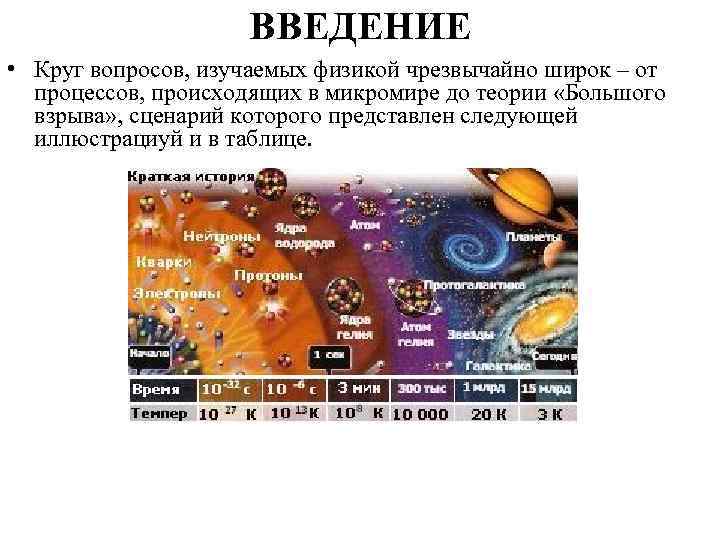ВВЕДЕНИЕ • Круг вопросов, изучаемых физикой чрезвычайно широк – от процессов, происходящих в микромире до теории «Большого взрыва» , сценарий которого представлен следующей иллюстрациуй и в таблице.

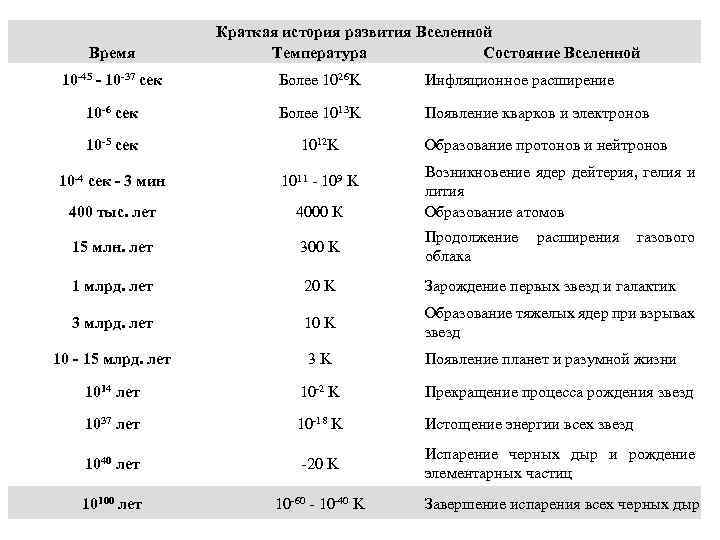Время Краткая история развития Вселенной Температура Состояние Вселенной 10 -45 - 10 -37 сек Более 1026 K Инфляционное расширение 10 -6 сек Более 1013 K Появление кварков и электронов 10 -5 cек 1012 K 10 -4 сек - 3 мин 1011 - 109 K 400 тыс. лет 4000 К 15 млн. лет 300 K Продолжение расширения газового облака 1 млрд. лет 20 K Зарождение первых звезд и галактик 3 млрд. лет 10 K Образование тяжелых ядер при взрывах звезд 10 - 15 млрд. лет 3 K Появление планет и разумной жизни 1014 лет 10 -2 K Прекращение процесса рождения звезд 1037 лет 10 -18 K Истощение энергии всех звезд 1040 лет -20 K Испарение черных дыр и рождение элементарных частиц 10100 лет 10 -60 - 10 -40 K Завершение испарения всех черных дыр Образование протонов и нейтронов Возникновение ядер дейтерия, гелия и лития Образование атомов

ВВЕДЕНИЕ • Достижения физики последних лет наглядно иллюстрируются следующими примерами. Графен Представьте себе углеродную пластину толщиной всего в один атом, но более прочную, чем алмаз, и пропускающую электричество в 100 раз лучше, чем кремний компьютерных чипов. — Графен — самый тонкий и самый прочный материал во вселенной, — заявил 19 июня английский физик Андре Гейм (Andre Geim) из Университета Манчестера.

ВВЕДЕНИЕ За «передовые опыты с двумерным материалом графеном» А. К. Гейму и К. С. Новосёлову была присуждена Нобелевская премия по физике за 2010 год

ВВЕДЕНИЕ 100 лет с момента открытия сверхпроводимости. В 1908 году нидерландский физик и химик Хейке Камерлинг-Оннес (1853 - 1926) впервые получил жидкий гелий и достиг рекордно низкой на тот момент температуры 0. 9 K. В 1911 году он впервые наблюдал резкое падение электрического сопротив-ления ртути при темперературе ниже 4. 1 K. Это явление получило название сверхпроводимоти. Нобелевская премия по физике 1913 г. Большой адронный коллайдер. Сверхпроводящий магнит длиной 29 км

ВВЕДЕНИЕ Телескоп Хаббл

ВВЕДЕНИЕ

I. Механика. Кинематика • Механика – раздел физики, изучающий простейшую форму движения материи – механическую, т. е. изменение положения тела в пространстве и во времени. Обычная или классическая механика справедлива для малых скоростей << и макроскопических размеров. Для скоростей сравнимых со скоростью света используется механика СТО, а для микромира – квантовая механика, которые в пределе переходят в классическую механику. Механика делится на кинематику, динамику и статику. • Кинематика изучает движение тел без учета действия сил (причин его вызывающих). • Динамика изучает движение тел под действием сил. • Статика изучает равновесие тел под действием сил. • Кинематика материальной точки • Материальная точка – тело, размерами которого в данных условиях можно пренебречь. Двигаясь в пространстве тело описывает некоторую кривую, называемую траекторией. В зависимости от ее формы движение бывает прямолинейным, криволинейным, по окружности и т. д. Для описания движения используется радиус-вектор, соединяющий в данный момент точку на траектории с началом координат.

I. Механика. Кинематика Расстояние 12 по траектории называют пройденным путем Ds, а по прямой – перемещением Dr. Для характеристики движения вводится средняя скорость на участке 12

I. Механика. Кинематика • При неравномерном движении средняя скорость постоянно меняется, поэтому вводят мгновенную скорость или просто скорость. • Модуль или величина скорости • . Скорость в данной точке направлена по касательной к траектории , Где - единичный вектор, определяющий направление касательной в данной точке траектории.

I. Механика. Кинематика • Для определния пройденного пути на конечном участке 12 траектории его необходимо разбить на отрезки • В пределе при получим • Ускорение – быстрота изменения скорости • Обратное соотношение имеет вид • .

I. Механика. Кинематика • Зная и начальные условия можно, используя связь между этими величинами получить уравнения движения • или . • Ускорение при криволинейном движении • В общем случае при криволинейном движении ускорение равно • В этом выражении вектор , оставаясь единичным по величине, все время меняет свое направление при переходе от одной точки траектории к другой. Введем понятие радиуса кривизны траектории, как радиуса окружности, которая заменяет бесконечно малый участок траектории в окрестности рассматриваемой точки. Вектор зависит от положения точки на траектории, характеризуемой расстоянием s от точки, принятой за начальную , а s – функция времени. Поэтому

I. Механика. Кинематика • - единичный вектор, поэтому . Продифференцируем это равенство • Каждый из векторов и отличен от нуля, поэтому угол между • ними равен 90°и перпендикулярен вектору , который • направлен по нормали к касательной в данной точке. • и , где - единичный вектор нормали

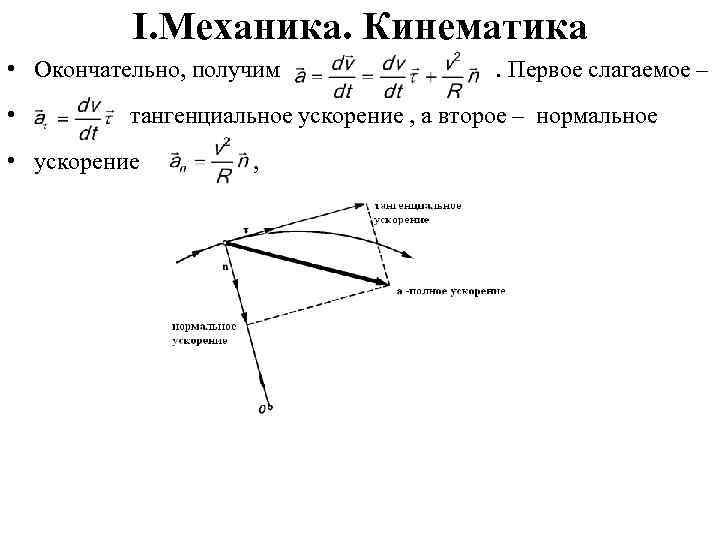I. Механика. Кинематика • Окончательно, получим . Первое слагаемое – • тангенциальное ускорение , а второе – нормальное • ускорение ,

I. Механика. Кинематика • Кинематика вращательного движения • При вращательном движении за время Dt точки тела опишут траектории разных радиусов, однако угол поворота будет одинаковый . Поэтому при вращательном движении вводят угловую скорость • , • где под направлением вектора угла поворота понимают направление перемещения правого винта. При равномерном вращении • , • За время одного оборота (период обращения T) и • . • Величину обратную Т называют частотой ( числом оборотов в секунду)

I. Механика. Кинематика Вектор угловой скорости может меняться по величине и направлению, поэтому вводят угловое ускорение Если направление оси вращения в пространстве не изменяется, то знаки векторов можно опустить, тогда , при совпадении направлений и и , если они направлены в противоположные стороны. Линейные и угловые величины при вращении связаны соотношением , откуда Итак, и

I. Механика. Динамика • Динамика изучает движение тел по действием сил. Основу динамики составляют 3 закона Ньютона. Первый закон. Если на тело не действуют другие тела или сумма их взаимодействий равно нулю, то тело сохраняет состояние покоя или прямолинейного равномерного движения, пока внешнее воздействие не заставит его изменить это состояние. Этот закон называют законом инерции, а системы отсчета, в которых он выполняется называются инерциальными. Любая система движущаяся прямолинейно и равномерно относительно данной инерциальной системы также является инерциальной. Инерциальной системой является гелиоцентрическая система, связанная с Солнцем. В большинстве случаев инерциальной является система отсчета, связанная с Землей. Сила – векторная величина, характеризующая воздействие на тело других тел или полей. Она определяет интенсивность и направление этого взаимодействия. Масса – мера инертности тела к изменению скорости его движения.

I. Механика. Динамика • Импульс - произведение массы тела на его скорость Ньютон сформулировал второй закон в следующем виде Для случая постоянной массы получим Эти уравнения , называемые уравнениями движения, применимы как к материальной точке, так и к протяженному телу, движущемуся поступательно. В случае действия нескольких сил, - их равно-действующая. Если , то ускорение тела равно нулю и мы получаем первый закон Ньютона. Однако, он рассматривается отдельно, как закон, определяющий существование инерциальных систем отсчета. Третий закон Ньютона –воздействие тел друг на друга всегда носит характер взаимодействия, при этом , где - сила, действующая со стороны первого тела на второе, - сила, действующая со стороны второго тела на первое.

I. Механика. Динамика • В природе существуют четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. • Сильное взаимодействие удерживает нуклоны в ядре, имеет радиус действия 10 -15 м и характеризуется временем протекания вызванных им процессов 10 -23 с. • Электромагнитное взаимодействие, лежащее в основе образования атомов и молекул и химических реакций, имеет неограниченный (бесконечный) радиус действия, константу взаимодействия порядка 10 -2 и характерное время протекания процессов 10 -16 с. • Слабое взаимодействие проявляется в b - распадах и реакциях синтеза, протекающих на Солнце и в звездах. Оно имеет радиус действия 10 -18 с, константу взаимодействия порядка 10 -6 и характерное время протекания процессов 10 -10 с. Несмотря на малую величину слабое взаимодействие лежит в основе энергетики Солнца и звезд (если его «выключить, то они погаснут). • Гравитационное взаимодействие играет существенную роль в макромире, определяющую образование и движение планет, звезд, галактик. Константа его взаимодействия порядка 10 -39, радиус действия, как и у электромагнитного взаимодействия, неограничен.

I. Механика. Динамика • Силы, рассматриваемые в механике имеют в своей основе гравитационное и электромагнитное взаимодействие. • Вес тела обусловлен действием на тело гравитационного притяжения Земли. Под весом понимают силу, с которой тело действует на основание, подставку, растягивает пружину, нить. • Сила трения возникает при трении поверхностей тел и движении тела в жидкой среде. В первом случае возникают силы сухого, а во втором – силы вязкого трения. Различают силу трения покоя и силу трения скольжения. Если несмотря на действие внешней силы тело находится на некоторой поверхности в состоянии покоя, то это является результатом возникновения силы трения покоя. Эта сила компенсирует действие внешней силы в следующих пределах: • , • • Где максимальная сила трения покоя– сила при которой начинается скольжение тела , а - сила нормального давления. Силы вязкого трения обусловлены трением слоев среды при движении тела в жидкости или газе и образованием дополнительного давления, на различные элементы поверхности тела.

I. Механика. Динамика Суммарная сила давления имеет составляющую, направленную в сторону, противоположную движению, и является силой сопротивления. Результирующая сила вязкого трения и сопротивления называется силой трения. При небольших скоростях она может быть представлена в виде: , а при больших скоростях , где и - коэффициенты пропорциональности, - единичный вектор, определяющий направление скорости. Рассмотрим систему N материальных точек и запишем для i –ой точки второй закон Ньютона: , где - сила взаимодействия i –ой и j –ой точки, а - внешняя сила, действующая на i –ую точку. Запишем систему уравнений для N материальных точек:

I. Механика. Динамика Просуммируем эти уравнения. Учитывая, что результирующая всех внутренних сил будет равна нулю, тогда получим: , где - полный импульс системы. Для системы тел результат записывается в виде: Если сумма внешних, действующих на систему равна нулю , то такая система называется замкнутой. Для такой системы и - импульс сохраняется. Закон сохранения импульса – импульс замкнутой системы сохраняется. Если система не является замкнутой, но сумма проекций внешних сил, например, на ось х равна нулю , то сохраняется проекция импульса системы на эту ось . Закон сохранения импульса связан с однородностью пространства – отсутствием в нем выделенных точек.

I. Механика. Движение центра масс системы Определим положение центра масс системы материальных точек: Скорость центра масс равна: , где - полный импульс системы. Подставляя это выражение в уравнение второго закона Ньютона для системы получим: Центр масс движется как материальная точка под действием всех приложенных внешних сил. Для замкнутой системы центр Масс движется прямолинейно равномерно или покоится.

I. Механика. Работа. Кинетическая энергия • В динамике для оценки действия на тело силы вводят величину работы силы. , где - сила, - перемещение под действием силы, - угол между силой и перемещением. При , при . Мощность - работа в единицу времени . Работа на конечном перемещении равна , Где - кинетическая энергия тела. Таким образом, работа равна изменению кинетической энергии.

I. Механика. Консервативные силы. Потенциальная энергия • Консервативные – силы, работа которых по перемещению тела не зависит от пути перемещения. Кроме контактного взаимодействия существуют взаимодействия с физическими полями – одной из форм существования материи. Тело может изменять свойства окружающего пространства, создавая в нем поле, например, гравитационное, электрическое и т. д. Задать поле – определить в каждой точке пространства силу. В гравитационном поле Земли на любое тело в каждой точке вблизи поверхности действует сила . Работа консервативных сил по замкнутому пути равна нулю. a 1 2 b При изменении направления перемещения знак работы меняется на противоположный. Поле однородно, если в любой точке силы, действующие на тело равны по величине и направлению. Если силы не зависят от времени, то поле стационарно.

I. Механика. Консервативные силы. Потенциальная энергия. • Силы в однородном стационарном поле консервативны • В центральном поле силы направлены в сторону неподвижного центра, зависят от r и в стационарном поле являются консервативными • , Потенциальная энергия – взятая с обратным знаком работа по перемещению материальной точки из начала координат в данную точку P Таким образом, работа в поле консервативных сил равна изменению потенциальной энергии. Для бесконечно малого перемещения по осям координат для работы можно написать:

I. Механика. Консервативные силы. Потенциальная энергия. Тогда сила связана с потенциальной энергией следующим соотношением , где Градиент направлен в сторону максимального увеличения соответствующей величины. Закон сохранения энергии. Для материальной точки , и Это есть закон сохранения энергии: полная энергия материальной точки равная сумме кинетической и потенциальной энергий сохраняется. Этот закон связан с однородностью времени (на оси времени нет выделенных точек). При рассмотрении механической системы необходимо учитывать силы взаимодействия между ее материальными точками (м. т. ). Если они консервативны, то можно ввести потенциальную энергию их взаимодействия как потенциальную энергию одной м. т. в поле

I. Механика. Закон сохранения энергии других м. т. Изменение кинетической энергии механической системы равно работе всех сил (внешних и внутренних), приложенным к ее материальным точкам, а изменение потенциальной энергии системы равно работе всех консервативных сил (внутренних и внешних), взятых с обратным знаком. Изменение механической энергии , где U – сумма потенциальной энергии взаимодействия материальных точек и потенциальной энергии системы во внешнем поле. Если неконсервативные силы отсутствуют , то полная энергия механической системы сохраняется. Системы в которых действуют только консервативные силы (как внутренние, так и внешние) называются консервативными. В консервативных системах полная механическая энергия сохраняется. Неконсервативные силы называют диссипативными, например – сила трения, их действие приводит к диссипации (рассеянию) энергии.

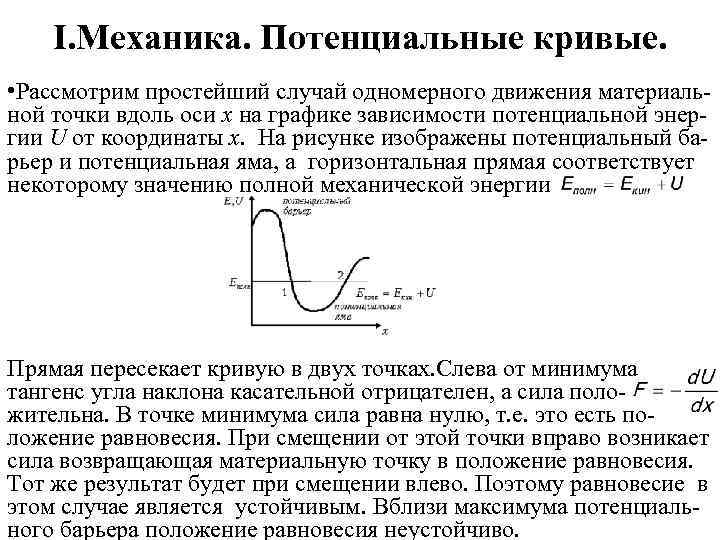I. Механика. Потенциальные кривые. • Рассмотрим простейший случай одномерного движения материальной точки вдоль оси x на графике зависимости потенциальной энергии U от координаты х. На рисунке изображены потенциальный барьер и потенциальная яма, а горизонтальная прямая соответствует некоторому значению полной механической энергии Прямая пересекает кривую в двух точках. Слева от минимума тангенс угла наклона касательной отрицателен, а сила положительна. В точке минимума сила равна нулю, т. е. это есть по- ложение равновесия. При смещении от этой точки вправо возникает сила возвращающая материальную точку в положение равновесия. Тот же результат будет при смещении влево. Поэтому равновесие в этом случае является устойчивым. Вблизи максимума потенциального барьера положение равновесия неустойчиво.

I. Механика. Неупругий и упругий удары. Пусть – полная энергия материальной точки. Полная энергия материальной точки . В точках 1 и 2 пересечения прямой полной энергии с потенциальной кривой полная энергия равна потенциальной, поэтому движение на участке 1 -2 возможно, а вне этого отрезка, где невозможно. Неупругий и упругий удары. Пусть два тела движутся вдоль прямой, соединяющей их центры, а после столкновения движутся вместе. Такой удар называется неупругим и центральным. Запишем закон сохранения импульса, где - масса и скорость первого тела, - масса и скорость второго тела, - скорость их совместного движения. При неупругом ударе действуют диссипативные силы, поэтому полная энергия не сохраняется. Рассмотрим упругий центральный удар двух тел и запишем для него законы сохранения импульса и энергии.

I. Механика. Неупругий и упругий удары. Перепишем уравнения. Собрав слева слагаемые, относящиеся к первому телу, а справа ко второму. Разделив первое уравнение на второе, получим Добавим к нему уравнение и решив полученную систему уравнений, получим.

I. Механика. Движение абсолютно твердого тела Абсолютно твердое – тело, взаимное расположение частиц которого во время движения не меняется. Поступательное – движение, при котором тело перемещается параллельно самому себе, а все его точки имеют одинаковую скорость и траектории одинаковой формы, параллельные другу. Вращательное – движение, при котором все точки твердого тела описывают окружности разных радиусов. Для случая плоского движения, при котором точки тела перемещаются в параллельных плоскостях , любое перемещение твердого тела можно представить как суперпозицию поступательного и вращательного движений. Для каждого момента времени всегда можно подобрать точку, скорость которой . Ее называют мгновенным центром вращения. Для плоского движения мгновенные центры вращения расположены на прямой, называемой осью вращения. Наиболее удобным оказывается разложение плоского движения тела на поступательное его центра масс и вращение вокруг оси, проходящей через этот центр.

I. Механика. Энергия движения твердого тела Центр масс твердого тела определяется также, как и для системы тел, суммирование заменяется интегрированием: Центр масс движется как материальная точка с массой, равной массе твердого тела под действием всех приложенных к телу внешних сил. Кинетическая энергия поступательного движения. Кинетическая энергия элемента твердого тела при поступательном движении с одинаковой для всех элементов скоростью равна: Суммируя по всем элементам, получим Кинетическая энергия вращательного движения. Кинетическая энергия элемента твердого тела при вращательном движении со скоростью равна

I. Механика. Энергия движения твердого тела Суммируя по всем элементам твердого тела, получим где момент инерции твердого тела – мера его инертности к изменению угловой скорости. Теорема Штейнера Момент инерции тела относительно произвольной оси вращения z´ равен сумме момента инерции тела относительно оси z, проходящей через центр масс и произведению массы тела на квадрат расстояния a между этими осями: Момент энергии материальной точки массой m на расстоянии R от оси вращения равен

I. Механика. Моменты инерции различных тел Момент инерции тонкого стержня массой m и длиной l Элемент массы стержня dm, длиной dx площадью сечения S, расположенный на расстоянии х от центра стержня равен . Интегрируя получим: . Момент инерции сплошного диска или цилиндра массой m и радиусом R

I. Механика. Моменты инерции различных тел Момент инерции тонкостенного диска или цилиндра (трубы) массой m и радиусом R равен . Момент инерции сплошного шара массой m и радиусом R равен: Полная кинетическая энергия движения твердого тела равна: Пример. Скатывание с высоты h наклонной плоскости без проскальзывания сплошного и полого цилиндров с одинаковыми массами m и внешними радиусами R.

I. Механика. Динамика вращательного движения твердого тела где с учетом отсутствия проскальзывания . Для скорости центра масс получим: У полого цилиндра момент инерции в два раза меньше, поэтому его скорость будет больше. Динамика вращательного движения твердого тела Момент силы относительно точки. Момент силы относительно оси (z). Если разложить силу на составляющие параллельно оси , перпендикулярно ей и по касательной к траектории вращения , то отличную от нуля проекцию на ось z даст

I. Механика. Динамика вращательного движения твердого тела только тангенциальная составляющая . Проекция момента будет равна Момент пары сил – момент, создаваемый парой сил равен где учтено. что Момент импульса относительно точки. Момент импульса относительно оси.

I. Механика. Динамика вращательного движения твердого тела Основное уравнение (второй закон Ньютона) вращательного движения (для материальной точки). Закон сохранения момента импульса. Если в уравнении , то и момент импульса сохраняется. Если , а , то сохраняется проекция момента импульса

I. Механика. Динамика вращательного движения твердого тела Основное уравнение (второй закон Ньютона) вращательного движения (для материальной точки). Основное уравнение (второй закон Ньютона) вращательного движения для системы материальных точек. Момент импульса системы – сумма моментов импульсов отдельных материальных точек для каждой материальной точки Суммируя по i, получим Силы взаимодействия между двумя материальными точками действуют в противоположные стороны вдоль одной и той же прямой, поэтому их моменты равны по величине. противоположны по

I. Механика. Динамика вращательного движения твердого тела направлению и попарно уравновешивают друга. Следовательно, и уравнение примет вид: Основное уравнение (второй закон Ньютона) вращательного движения твердого тела относительно неподвижной оси. С учетом рассмотренного выше уравнения вращательного движения для системы материальных точек, получим: . где , - проекции на ось вращения z момента импульса и момента внешних сил. Момент импульса твердого тела равен Тогда уравнение примет вид:

I. Механика. Динамика вращательного движения твердого тела Задача. Сплошной цилиндр массой m, c моментом инерции I и радиусом R скатывается без проскальзывания с наклонной плоскости, образующей с горизонтом угол a. Определить его ускорение. Запишем второй закон Ньютона для посту- пательного и вращательного движений , где ось вращения проходит через ось симметрии цилиндра, поэтому сила тяжести и сила нормального даувления моментов сил не создают. Угловое ускорение и ускорение поступательного движения связаны соотношением , а момент силы трения . Тогда второе уравнение преобразуется к виду: Складывая его с первым уравнением получим: Этот результат можно использовать и для полого цилиндра и для шара. Для сплошного цилиндра , где учтено, что

I. Механика. Динамика вращательного движения твердого тела Закон сохранения момента импульса. Если в уравнении , то и момент импульса сохраняется. Если , а , то сохраняется проекция момента импульса . Для системы тел: , если , то Для твердого тела . Если , то Закон сохранения импульса связан с изотропностью пространства отсутствием в пространстве выделенных направлений.

I. Механика. Гравитационное поле. Закон всемирного тяготения Для материальных точек и тел сферической формы Закон записывается в следующем виде: Выражение для ускорения свободного падения на поверхности Земли можно получить следующим образом: , откуда , где m – масса тела, M – масса Земли, R – ее радиус. На высоте h от поверхности Земли и для ускорения свободного падения получим . Движение спутников планет по круговым орбитам. Запишем для этого движения второй закон Ньютона: ,

I. Механика. Гравитационное поле. где m – масса спутника, M – масса планеты, R – ее радиус, h –высота орбиты над поверхностью планеты, - ускорение свободного падения на ее поверхности. Из этого уравнения можно найти скорость спутника и ее период обращения Т. Если , т. е спутник летает на небольшой высоте, тогда скорости получим: и для первой космической . - скорость, которую необходимо сообщить телу, чтобы оно стало спутником Земли (не вернулось на Землю). Эллиптические орбиты. В общем случае движение планет и их спутников происходит по эллиптическим орбитам. Гравитационные силы Солнца или планет не создают момента силы, поэтому момент импульса планет или спутников сохраняется.

I. Механика. Гравитационное поле. и - радиус орбиты и скорость на орбите в перигее, а и радиус и скорость в апогее. Между ними существует следующее соотношение. Потенциальная энергия гравитационного поля. Рассмотрим гравитационное взаимодействие материальной точки массой m и шара (Земли) массой M и радиуса R. Беря неопределенный интеграл, получим: Если потенциальная энергия обращается в ноль на бесконечности, то константа интегрирования С=0 и Если принять потенциальную энергию равной нулю на поверхности шара (Земли) и , а потенциальная

I. Механика. Гравитационное поле. Потенциальная энергия в этом случае принимает вид: Если высота над поверхностью шара (Земли) мала , то и Получаем известное выражение для потенциальной энергии тела на высоте h от поверхности Земли. Вторая космическая скорость – скорость, которую необходимо сообщить телу, чтобы оно покинуло поле притяжение Земли (удалилось от него на бесконечность). Если принять потенциальную энергию на бесконечности, равной нулю, то закон сохранения энергии запишется в виде: , где выражение в правой части равенства – полная энергия тела на поверхности Земли. На бесконечно большом расстоянии от Земли кинетическая и потенциальная энергии обращаются в ноль и

I. Механика. Специальная теория относительности Кинематика специальной теории относительности Преобразования Галилея Координаты материальной точки, покоящейся в системе К’ , в системе отсчета К будут иметь следующие координаты: Время в классической механике считается абсолютным, поэтому . Полученные соотношения называются преобразованиями Галилея. Соответствующие компоненты скорости имеют вид:

I. Механика. Специальная теория относительности • Постоянство скорости света. Опыт Майкельсона и Морли. • Для проверки существовавшей в конце 19 - начале 20 века теории эфира был проведен эксперимент Майкельсона и Морли. В нем измерялось время прохождения света в интерферометре в направлении движения Земли по орбите и в перпендикулярном направлении. Несмотря на высокую точность прибора время прохождения света оказалось не зависящим от направления движения: скорость света не складывалась (не вычиталась) со скоростью движения Земли. Скорость света оказалась постоянной, а преобразования Галилея не выполнялась. • В результате был сформулирован принцип относительности Эйнштейна: 1. Скорость света инвариантна относительно инерциальных систем отсчета и в пустоте не зависит от движения источника и приемника света; 2. Все законы природы инвариантны относительно инерциальных систем отсчета. • Постоянство скорости света требует, чтобы в системах К и К’ распространяющаяся световая волна имела сферический фронт. • •

I. Механика. Специальная теория относительности Подстановка преобразований Галилея дает: . Системе уравнений (1) и (2) удовлетворяют преобразования Лоренца. • Обратные преобразования имеют вид: Сложение скоростей:

I. Механика. Специальная теория относительности Разделив на dt, получим: где Постоянство скорости света приводит к разному течению времени в системах К и К’. Одновременность двух событий требует экспериментальной проверки. Одновременность событий происходящих в одной точке пространства определяется одними часами, а в разных точках только различными часами. Возникает проблема их синхронизации. Путем переноса синхронизированных часов из одной точки в другую она не решается, т. к. неизвестно, как меняется ход часов в процессе переноса. Поэтому синхронизацию необходимо провести в разных точках пространства, используя световой импульс, имеющий скорость с во всех инерциальных системах отсчета.

I. Механика. Специальная теория относительности • Часы в точке А синхронизованы с часами в точке В, если при достижении сигналом, испущенным из А в момент , часов В они показывают время , где - время возвращения сигнала к часам в А. Если теперь такие часы показывают одинаковое время двух событий, то они одновременны. Пусть два события происходят одновременно в системе К’ в точках и , Тогда, если , то . События в системе К происходят одновременно в одной точке пространства. Если , то и , т. е. события в системе К не одновременны.

I. Механика. Специальная теория относительности Продолжительность событий в разных системах отсчета. Замедление времени. Пусть время между событиями в системе К’ в точке . Определим время между теми же событиями в системе К. Время определено по часам, движущимся вместе с системой К’ и неподвижным относительно тела. Время определено по часам в системе К, которые движутся относительно тела. Промежуток времени по часам, связанным с телом ( собственное время) всегда меньше промежутка времени по часам, движущимся относительно тела . • Эффект замедления времени наблюдается при распаде - мезона. Среднее время его жизни (до распада) в покое составляет

I. Механика. Специальная теория относительности Однако, образуясь в космических лучах, мезоны долетают до Земли (20 -30 км). С точки зрения наблюдателя, движущегося с мезоном, его время замедляется по сравнению с часами на Земле. Сокращение длины движущегося тела. Рассмотрим стержень длины , расположенный неподвижно вдоль оси в системе К’ . Измерим (одновременно в момент времени ) координаты стержня в системе К: , откуда Таким образом, при движении длина стержня сокращается в направлении движения. Вдоль осей y и z размеры стержня не меняются. Элементы динамики специальной теории относительности. Рассмотрим неупругий удар двух одинаковых шаров вдоль оси в системе К

I. Механика. Специальная теория относительности В системе К’ В системе К импульс сохраняется , а в системе К’ не сохраняется. Это происходит потому, что импульс тела меняется при переходе от одной системы отсчета к другой. В релятивистской механике он имеет вид 2 закон Ньютона в специальной теории относительности.

I. Механика. Специальная теория относительности Кинетическая энергия релятивистской частицы Рассмотрим работу силы Для энергии движущейся релятивистской частицы получим: При и называется энергией покоя. Кинетическая энергия равна:

I. Механика. Специальная теория относительности При и выражение для кинетической энергии переходит к классическому виду. Нетрудно видеть, что Тогда полная энергия и импульс связаны соотношением: