
Кучи heap

куча ► это абстрактный тип данных, предназначенный для представления взвешенных множеств, имеет свойство ключ элемента превосходит ключи, его потомков. Множество называется взвешенным, если каждому его элементу однозначно соответствует число, называемое ключом или весом.

Бинарная куча (binary heap) ► Множество, обладающее определенными свойствами упорядоченности: § - нулевой элемент множества – корень § - для каждого элемента множества по индексу можно определить левую и правую дочерние вершины § - значение предка должно быть больше потомков Представлено в виде сортирующего дерева

► Бинарная куча == ► очередь с приоритетами == ► сортирующее дерево

Область использования ► сортировка элементов массива ► поиск во взвешенном неориентированном графе минимального остовного дерева ► поиск кратчайших путей от заданной вершины взвешенного графа до его остальных вершин ► и другие.

каждая вершина: ► ключ (key) ► информационное поле

Реализация ► на основе дерева ► на основе массива § неэффективны по времени выполнения основных операций: поиск, для поддержки упорядоченность массива по ключу, "неудобна" операция вставки нового элемента.
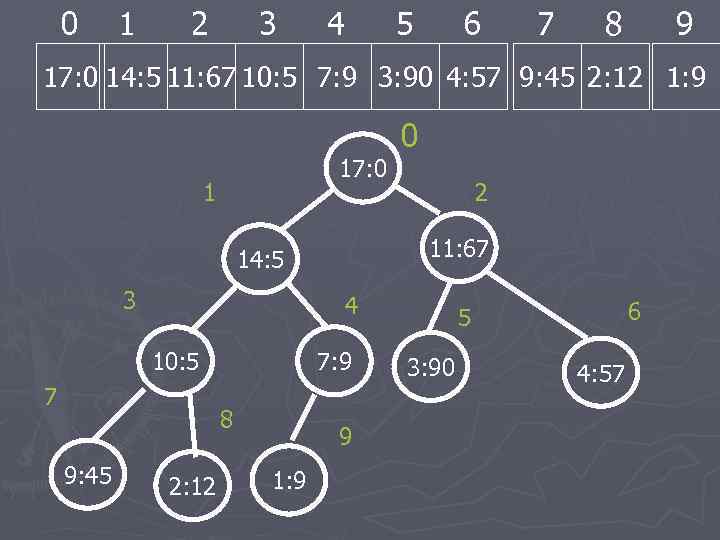
0 1 2 3 4 5 6 7 8 9 17: 0 14: 5 11: 67 10: 5 7: 9 3: 90 4: 57 9: 45 2: 12 1: 9 0 17: 0 1 11: 67 14: 5 3 4 10: 5 7 7: 9 8 9: 45 2 2: 12 9 1: 9 6 5 3: 90 4: 57
![► Основное свойство кучи: для любого i (кроме корня) A[parent(i)]>=A[i] (i-1)/2 i 2 i+1 ► Основное свойство кучи: для любого i (кроме корня) A[parent(i)]>=A[i] (i-1)/2 i 2 i+1](https://present5.com/presentation/3/212312989_187965485.pdf-img/212312989_187965485.pdf-9.jpg)
► Основное свойство кучи: для любого i (кроме корня) A[parent(i)]>=A[i] (i-1)/2 i 2 i+1 2 i+2

► Где находиться наибольший элемент кучи? ► Является ли кучей массив <23, 17, 14, 6, 13, 10, 1, 5, 7, 12> ?

► Размер свойства кучи - это количество вершин в ней ► Высота вершины дерева (максимальная глубина) – высота поддерева с корнем в этой вершине (число ребер в самом длинном пути с началом в этой вершине вниз по дереву к листу) ► в куче все уровни кроме последнего заполнены ► Высота дерева = высота корня ► N – число элементов

► Высота кучи и размер? ► <23, 17, 14, 6, 13, 10, 1, 5, 7, 12>

Основные операции ► Проверка основного свойства кучи Heapify время работы - O(logn) ► Построение кучи из произвольного массива Build. Heap - O(n) ► Сортировка массива без использования дополнительной памяти Sort. Heap -O(nlogn) ► Извлечение наибольшего (очередь с приоритетами) Extract. Max - O(logn) ► Мах - O(1) ► Добавление элемента Insert. Heap - O(logn)

Дополнительные операции ► Объединение двух куч – Union ► Удаление из кучи Delete ► Уменьшить значения ключа - Decrease. Key
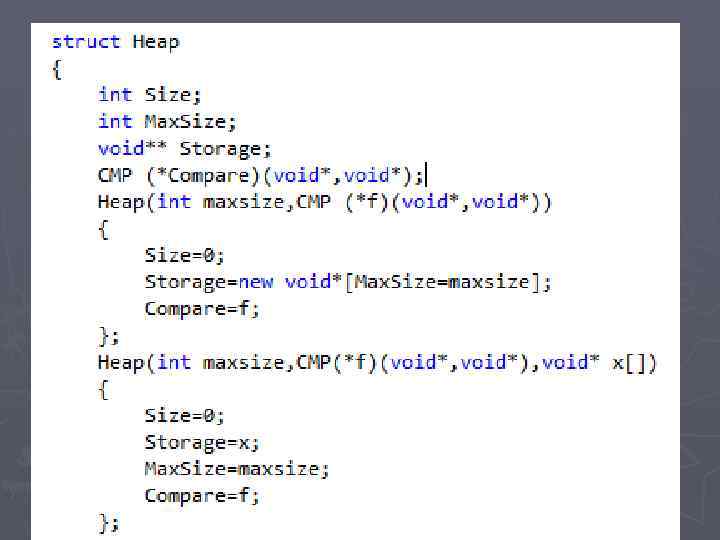

Определение родительской вершины

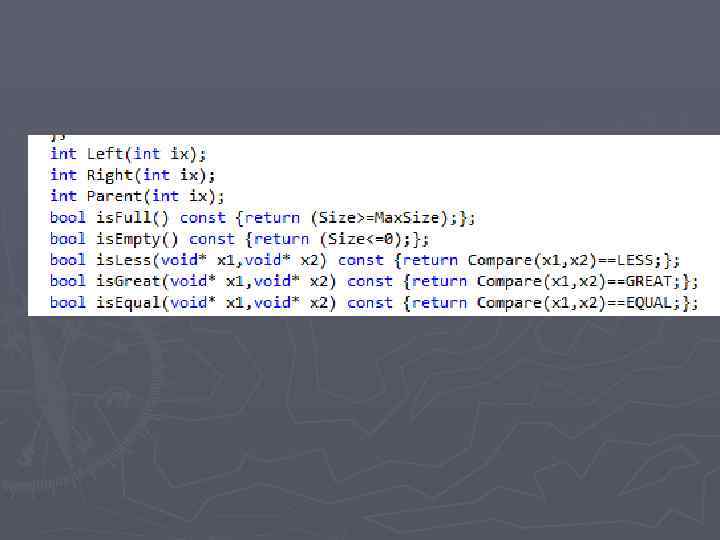
Определение левой дочерней вершины
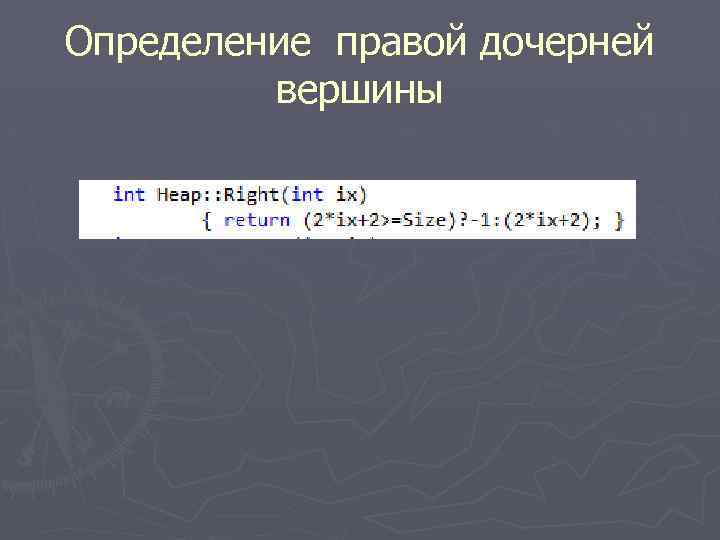
Определение правой дочерней вершины
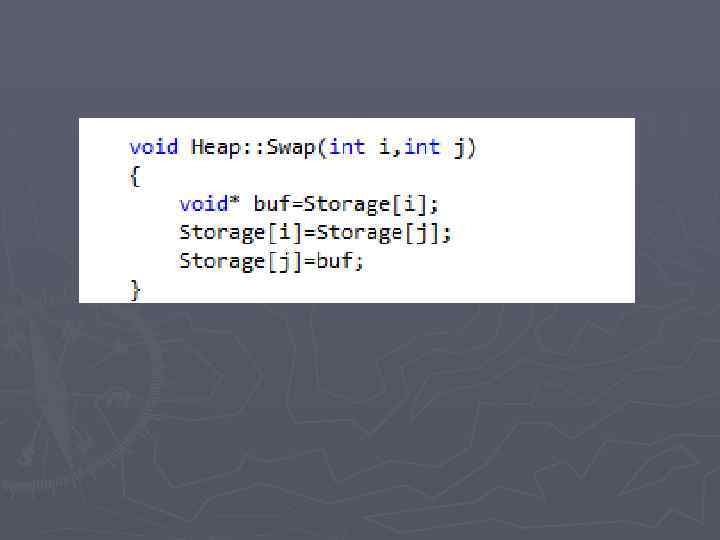

Проверка основного свойства кучи
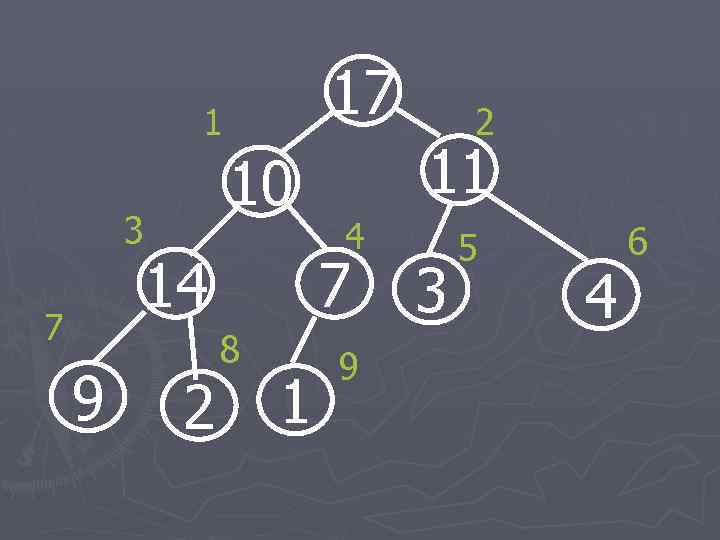
17 1 10 3 14 7 9 2 11 4 7 8 1 2 9 3 5 4 6

Оценка ►N - общее число элементов кучи ► h - глубина кучи ► - число элементов на самом нижнем уровне. ►

Минимальное число узлов в куче N min = 1+21+22+ … +2 h-1+1= Максимальное число узлов в куче N max = 1+21+22+ … +2 h-1+2 h= 2 h≤N ≤ 2 h+1 -1 (Количество узлов высоты h) ≤ N/2 h

cложность heapify ► O(1)- сложность фиксированной части, ► T(k) - сложность обработки следующего поддерева. ► общая сложность будет: T(N)=O(1)+T(k) ► T(N)<=O(h) ► h=log 2 N => T(N)=O(log 2 N)
![Построение кучи из произвольного массива Массив x[1. . N] Heapify к массиву в порядке Построение кучи из произвольного массива Массив x[1. . N] Heapify к массиву в порядке](https://present5.com/presentation/3/212312989_187965485.pdf-img/212312989_187965485.pdf-26.jpg)
Построение кучи из произвольного массива Массив x[1. . N] Heapify к массиву в порядке убывания начиная с вершины c [(N-1)/2] - удовлетворяют основному свойству
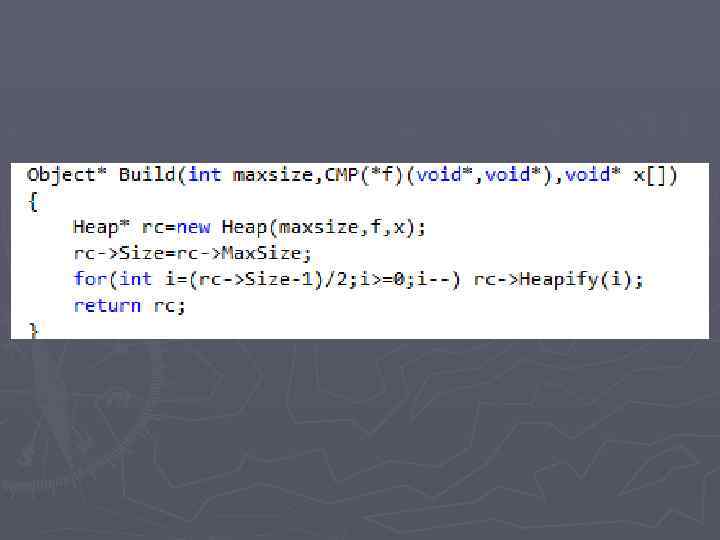
![Оценка сложности ► Временная сложность ► T(N)<=[(N-1)/2]*Theapify(N) = =[(N-1)/2]*O(log 2 N) Оценка сложности ► Временная сложность ► T(N)<=[(N-1)/2]*Theapify(N) = =[(N-1)/2]*O(log 2 N)](https://present5.com/presentation/3/212312989_187965485.pdf-img/212312989_187965485.pdf-28.jpg)
Оценка сложности ► Временная сложность ► T(N)<=[(N-1)/2]*Theapify(N) = =[(N-1)/2]*O(log 2 N)
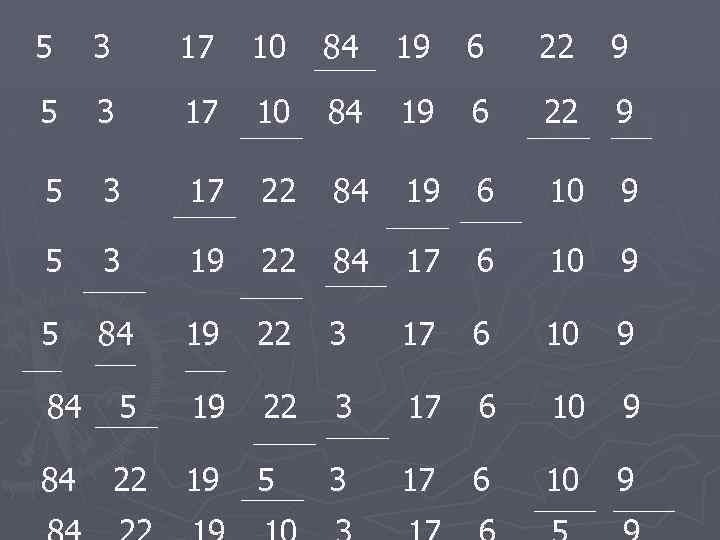
5 3 17 10 84 19 6 22 9 5 3 17 22 84 19 6 10 9 5 3 19 22 84 17 6 10 9 5 84 19 22 3 17 6 10 9 84 5 19 22 3 17 6 10 9 84 22 19 5 3 17 6 10 9

Сортировка массива без использования дополнительной памяти Sort. Heap 1. 2. 3. 4. выполнить процедуру Build. Heap; обменять местами элементы A[0] и A[n-1]; уменьшить размер кучи на единицу: выполнить процедуру Heapify для элемента 0 и т. д.

![Оценка сложности ► T[N] sort=T[N] buildheap+ (N-1)T[N] heapify T[N]=O(N)+(N-1)(O(log. N)+O(1))= =O(N)+O(Nlog. N)= =O(Nlog 2 Оценка сложности ► T[N] sort=T[N] buildheap+ (N-1)T[N] heapify T[N]=O(N)+(N-1)(O(log. N)+O(1))= =O(N)+O(Nlog. N)= =O(Nlog 2](https://present5.com/presentation/3/212312989_187965485.pdf-img/212312989_187965485.pdf-32.jpg)
Оценка сложности ► T[N] sort=T[N] buildheap+ (N-1)T[N] heapify T[N]=O(N)+(N-1)(O(log. N)+O(1))= =O(N)+O(Nlog. N)= =O(Nlog 2 N)
![Извлечение наибольшего Extract. Max ►Сохранить значение A[0] в промежуточной памяти ►Записать значение последнего элемента Извлечение наибольшего Extract. Max ►Сохранить значение A[0] в промежуточной памяти ►Записать значение последнего элемента](https://present5.com/presentation/3/212312989_187965485.pdf-img/212312989_187965485.pdf-33.jpg)
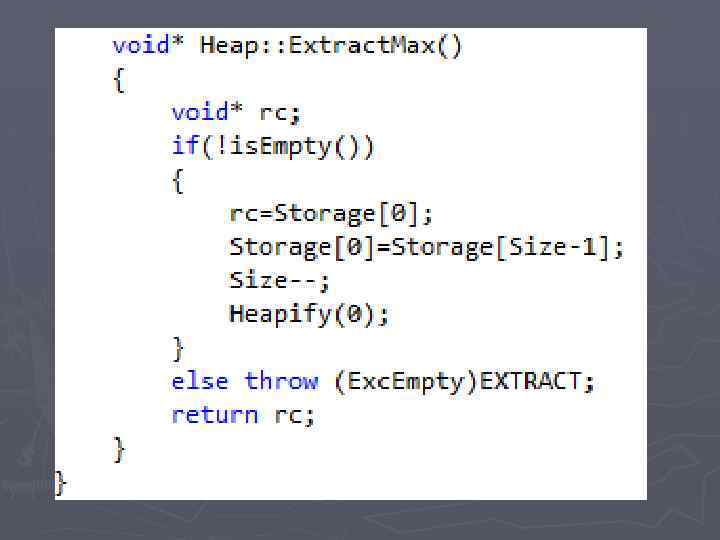
Извлечение наибольшего Extract. Max ►Сохранить значение A[0] в промежуточной памяти ►Записать значение последнего элемента A[N-1] в A[0] ►Уменьшить на единицу размер кучи ►Выполнить Heapify для 0 Сложность алгоритма O(log 2 N)
![Оценка сложности ► T[N]=T[N]heapify + O(1)= =O(log 2 N)+O(1)=O(log 2 N) Оценка сложности ► T[N]=T[N]heapify + O(1)= =O(log 2 N)+O(1)=O(log 2 N)](https://present5.com/presentation/3/212312989_187965485.pdf-img/212312989_187965485.pdf-35.jpg)
Оценка сложности ► T[N]=T[N]heapify + O(1)= =O(log 2 N)+O(1)=O(log 2 N)

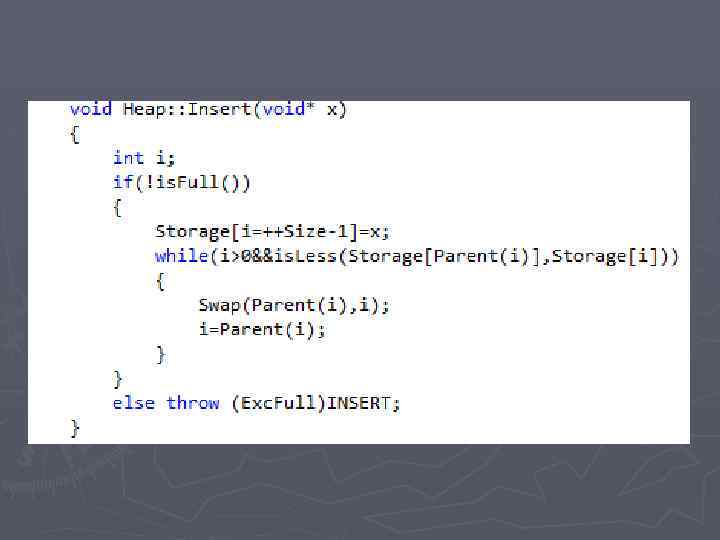
Добавление элемента Insert. Heap ►Увеличить на один размер кучи ►Поместить новый элемент за последним элементом кучи ►Дать всплыть элементу до своего уровня Временная сложность алгоритма O(log 2 N) – глубина дерева

Очередь с приоритетами (priority queue) ► <key, info> ► Insert(S, x) ► Maximum (S) ► Extract. Max(S) ► разделение ресурсов в операционной системе ► управление событиями (event-driven simulation)

d-ичная куча d≥ 2 определение дочерних вершин высота кучи через d и n di узлов глубины i
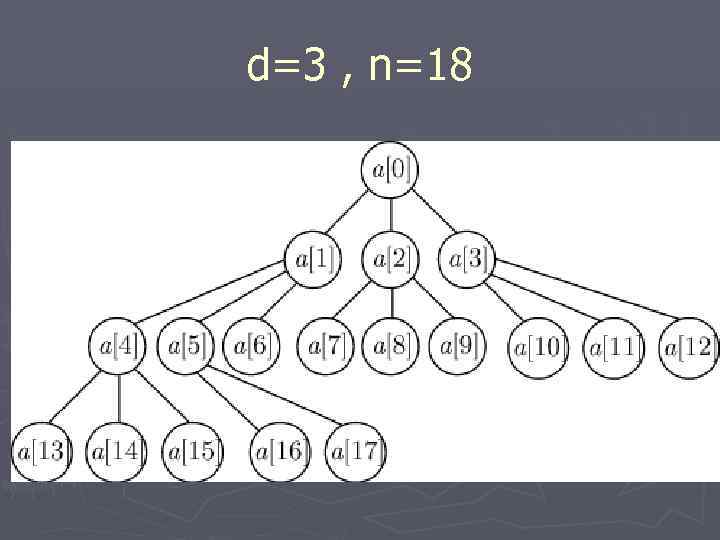
d=3 , n=18
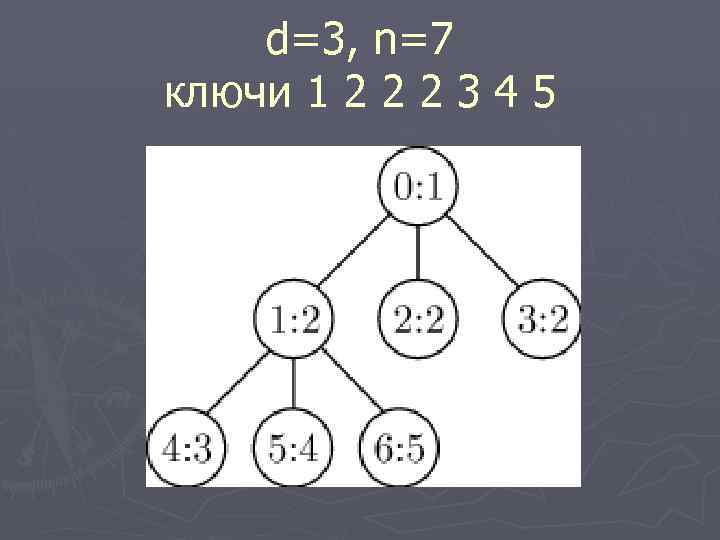
d=3, n=7 ключи 1 2 2 2 3 4 5

Левосторонние кучи ► Левосторонняя куча — бинарное дерево, для каждого узла которого ранг его левого непосредственного потомка в расширенном дереве не меньше ранга его правого потомка. ► Ранг узла - уменьшенное на 1 расстояние (число ребер) от него до ближайшего неполного потомка.

Свойства левостороннего дерева ► Правая ветвь из любого узла дерева имеет минимальную длину среди всех ветвей, исходящих из этого узла. ► Длина правой ветви левостороннего дерева, имеющего N узлов ограничена c[log 2 N].
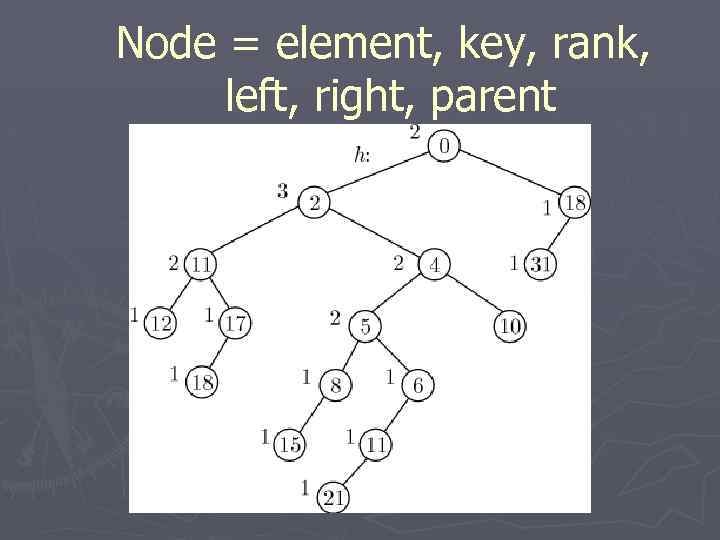
Node = element, key, rank, left, right, parent

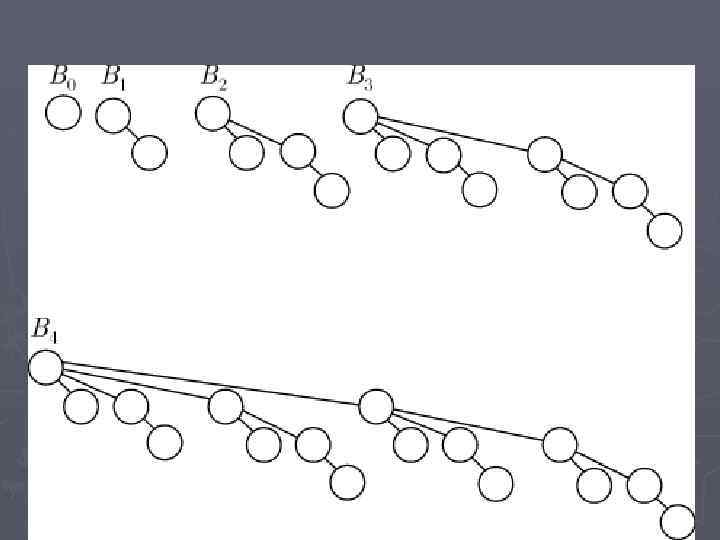
Биномиальное дерево ► B 0 — дерево, состоящее из одного узла высоты 0; ► Bk - дерево высоты k формируется из двух деревьев Bk-1 , при этом корень одного из них становится потомком корня другого. ► Биномиальный лес — это набор биномиальных деревьев, в котором любые два дерева имеют разные высоты.

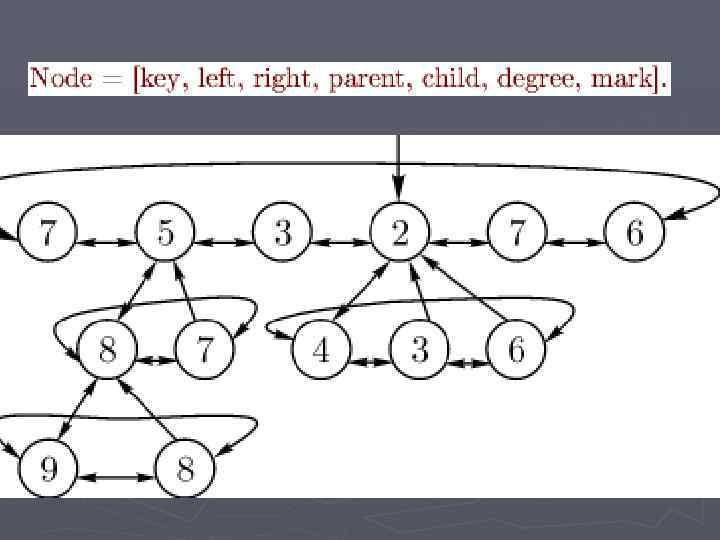
Фибоначчиева куча (англ. Fibonacci heap) ► время работы операций не требующих удаления- равно O(1) ► удаление O(logn)

► Каждое набор деревьев дерево в H подчиняется свойству неубывающей пирамиды (min-heap property): ключ узла не меньше ключа его родительского узла. ► Каждый узел x в H содержит след. указатели и поля: ► key[x] — поле, в котором хранится ключ; ► p[x] — указатель на родительский узел; ► child[x] — указ. на один из дочерних узлов; ► left[x] — указ. на левый сестринский узел; ► right[x] — указ. на правый сестринский узел; ► degree[x] — поле, в кот хранится кол. дочер. узлов; ► mark[x] — лог знач. , кот указывает, были ли потери узлом x дочерних узлов, начиная с момента, когда x стал дочерним узлом какого-то другого узла.

► Дочерние узлы x объединены при помощи указателей left и right в один циклический дважды связанный список дочерних узлов (child list) x. ► Корни всех деревьев в H связаны при помощи указателей left и right в циклический дважды связанный список корней (root list). ► Обращение к H выполняется посредством указателя min[H] на корень дерева с минимальным ключом. Этот узел называется минимальным узлом (minimum node) H.

► Подготовиться 16. 05. 2013 к контрольной ► Темы: ► Оценка алгоритмов, стеки, очереди, деки, списки, рекурсия, деревья, кучи, хэш