Кубичная среда Четырехволновое ваимодействие 1 г Электроиндуцированная

Кубичная среда Четырехволновое ваимодействие 1

г) Электроиндуцированная вторая гармоника д) Магнитоиндуцированная вторая гармоника 2

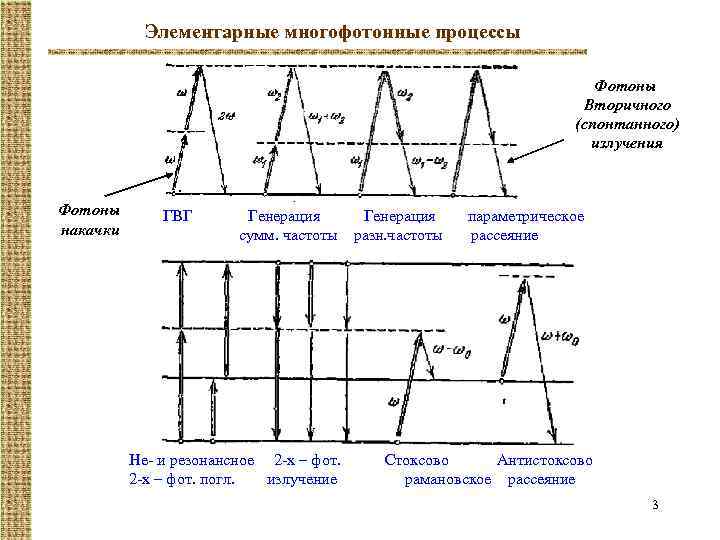
Элементарные многофотонные процессы Фотоны Вторичного (спонтанного) излучения Фотоны накачки ГВГ Генерация сумм. частоты Не- и резонансное 2 -х – фот. погл. излучение Генерация разн. частоты параметрическое рассеяние Стоксово Антистоксово рамановское рассеяние 3

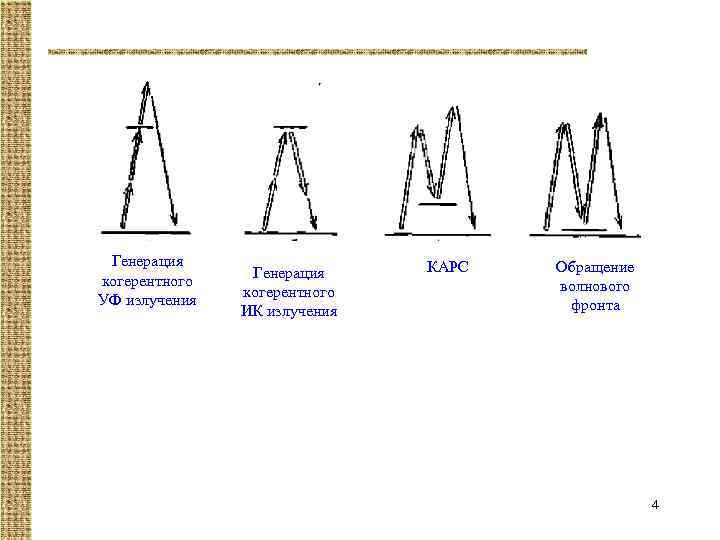
Генерация когерентного УФ излучения Генерация когерентного ИК излучения КАРС Обращение волнового фронта 4

Феноменологическое описание восприимчивостей среды I. Линейная восприимчивость Для однородного пространства и стационарности во времени имеем: В локальном приближении полагаем: В выражении для плоской монохроматической волны (иначе, для Фурьекомпоненты ЭМ поля): сделаем замену переменных: 5

Тогда интегральное выражение переходит в алгебраическую связь между спектральными компонентами поляризации, восприимчивости и ЭМ поля: функция Хевисайда Фурье-компонента линейной восприимчивости В общем случае поле с произвольной зависимостью от времени можно разложить в интеграл Фурье - дальше будем работать с Фурье-образами. При этом выполняются некоторые универсальные соотношения между самой функцией времени и её Фурье-образом 6

Если функция вещественна, тогда четная функция нечетная функция Отсюда следует, что, хотя формально Фурье-образ определен для частот от - ∞ до + ∞ , реально (с учетом четности) его можно задавать только для + ∞ ( ) Из вещественности поляризации и поля а также соотношений следует универсальное свойство линейной восприимчивости: 7

Из принципа симметрии кинетических коэффициентов (принципа Онсагера) следует: ! принцип Онсагера справедлив только в отсутствие магнитного поля. Для гиротропных (магнитных или оптически активных) сред свойство трансформируется в 8

Квадратичная восприимчивость (нелинейная восприимчивость второго порядка). В однородной восприимчивость имеет вид: стационарной среде квадратичная нелинейная Пренебрегая нелокальностью: 9

Для бигармонического ЭМ поля: Спектральная компонента квадратичной поляризации: получаем алгебраическое выражение где спектральная компонента квадратичной восприимчивости 10

Общие свойства восприимчивостей Перестановочная симметрия по всем индексам, кроме первого с соответствующей перестановкой частотных аргументов: Из вещественности ЭМ полей и поляризации следует универсальное свойство восприимчивостей: Покажем это… 11

Действительн о: тогда: поскольку меняя знаки частот в обеих частях выражения, получим: 12

Поглощение в заданном поле Диссипируемая мощность в слабо поглощающей среде: Здесь вектор Пойнтинга: C другой стороны, в немагнитной среде система макроскопических уравнений Максвелла имеет вид : 13

Средняя по времени поглощаемая мощность ЭМ излучения если то средняя по периоду поглощаемая мощность определяется амплитудами поля и Р Потери определяются произведением мнимой части восприимчивости и 14 амплитуд полей

Симметрия по всем индексам в среде без поглощения: соотношения Клейнмана Покажем на примере (2) возможность перестановки по первому индексу в нерезонансном случае – если все частоты лежат вне резонансов вещества. Реальной диссипации нет, изменение энергии в каждой из мод связано только с перекачкой в другие моды. Парциальные мощности : Изменим это выражение так, чтобы всюду было одинаковое произведение полей. 15

Поскольку получим: Если все 3 частоты лежат вне резонансов, то поглощение отсутствует и вещество лишь перераспределяет энергию между компонентами поля с 2, и 3. Т. к. комплексные амплитуды произвольны, то: Более того, в отсутствие дисперсии также произвольны и коэффициенты по отдельности равны нулю - получаем полную перестановочную симметрию по всем трем индексам 16

Соотношения Менли-Роу Перестановочная симметрия по первым индексам в отсутствие поглощения приводит к соотношениям Менли-Роу: Коэффициенты Миллера (1964) 17

Факторы локального поля Для кубической (изотропной) среды 18

Влияние кристаллической структуры на вид тензора нелинейной восприимчивости Принцип Неймана: симметрия макросвойства - не ниже симметрии структуры (группа симметрии свойства должна включать все элементы симметрии структуры) Конкретный вид тензора, описывающего конкретное свойство кристалла, определяется кристаллической симметрией. Компоненты тензора преобразуются как соответствующие произведения проекций векторов. Например, для квадратичной восприимчивости : эквивалентно преобразованию 19

Преобразование - это некоторая операция симметрии и соответствующая матрица перехода: x y z x' a 11 a 12 a 13 y' a 21 a 22 a 23 z' a 31 a 32 a 33 Таким образом, симметрийное преобразование имеет вид: 20

21

22

23

24

25

26