Kryptosysteme Digitale Signaturen Keymanagement Digitale Signaturen Jürgen Ecker

Kryptosysteme, Digitale Signaturen, Keymanagement Digitale Signaturen Jürgen Ecker

Inhalt Einführung RSA-Signaturen PKCS #1 ISO 9796 El. Gamal-Signaturen DSS Folie 2

Klassifikation Digitale Signaturen mit message recovery Aus der Signatur kann die signierte Nachricht ermittelt werden, diese braucht nicht zusätzlich gesendet zu werden. Digitale Signaturen ohne message recovery Die signierte Nachricht ist zweiteilig, die Nachricht wird zusätzlich zur Signatur benötigt, um die Unterschrift überprüfen zu können. Randomisierte Signaturschemata Die Signatur hängt außer von der Nachricht und vom Schlüssel auch noch von einem zufälligen Parameter ab. Deterministische Signaturschemata Die Signatur hängt nur von der Nachricht und vom Schlüssel ab. Folie 3

RSA-Signaturen mit message recovery Setup: Wähle RSA Schlüsselpaar (n, e), (n, d) Wähle eine Redundanzfunktion R, die Nachrichten zu Zahlen zwischen 1 und n-1 macht (vorerst beliebig). Signieren von m: berechne m´ = R(m) Redundanz hinzufügen berechne s = (m´)d mod n Signieren Verifizieren von s: berechne m´ = se mod n Signatur öffnen prüfe, ob m´ in R(M) liegt Redundanz prüfen berechne m = R-1(m´) message recovery Folie 4

RSA-Signaturen mit message recovery Zur Redundanzfunktion Die Redundanzfunktion ist so zu wählen, dass es praktisch unmöglich ist, ohne den private key eine Signatur s zu erzeugen, so dass se mod n in R(M) liegt, d. h. die geforderte Redundanz besitzt. Beispiel: Die Funktionswerte von R sind immer von der Form x x Folie 5

RSA Signaturen in der Praxis: ISO/IEC 9796 Eigenschaften für PK Signaturschemata, die aus k-Bit Nachrichten k-Bit Signaturen erzeugen zum Signieren von Nachrichten begrenzter Länge keine Hashfunktion benötigt message recovery Folie 6

ISO/IEC 9796: Notation Symbol Bedeutung k Bitlänge der Signatur d Bitlänge der zu signierenden Nachricht; z d ≤ 8 (k+3)/16 z = d/8 r Anzahl der Füllbits +1: r = 8 z-d+1 t t = (k-1)/16 ; 2 t Bytes enthalten zumindest k-1 Bits Beispiel: k=1024, d=150, z=19, r=3, t=64 Folie 7

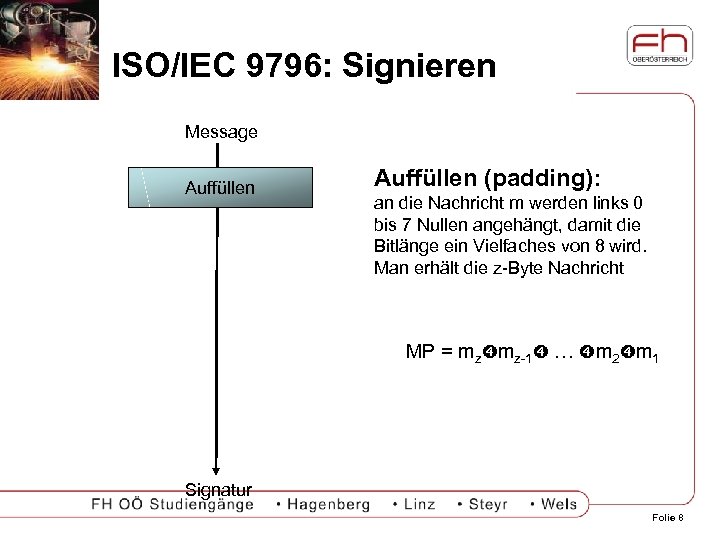ISO/IEC 9796: Signieren Message Auffüllen (padding): an die Nachricht m werden links 0 bis 7 Nullen angehängt, damit die Bitlänge ein Vielfaches von 8 wird. Man erhält die z-Byte Nachricht MP = mz mz-1 … m 2 m 1 Signatur Folie 8

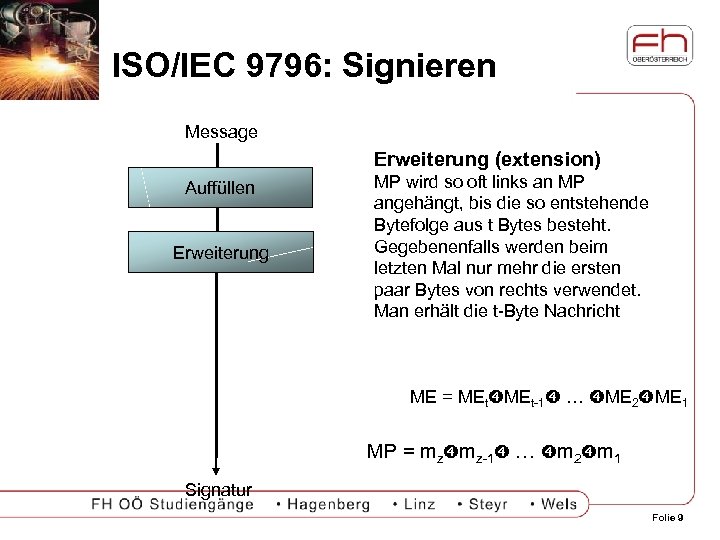ISO/IEC 9796: Signieren Message Erweiterung (extension) Auffüllen Erweiterung MP wird so oft links an MP angehängt, bis die so entstehende Bytefolge aus t Bytes besteht. Gegebenenfalls werden beim letzten Mal nur mehr die ersten paar Bytes von rechts verwendet. Man erhält die t-Byte Nachricht ME = MEt-1 … ME 2 ME 1 MP = mz mz-1 … m 2 m 1 Signatur Folie 9

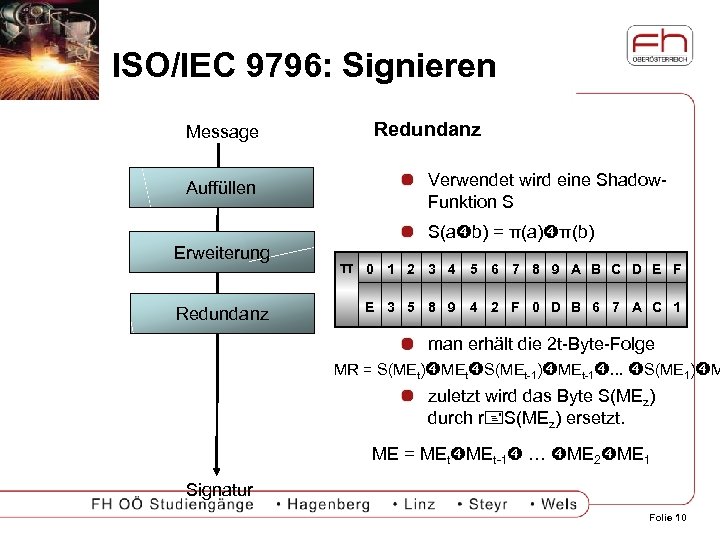ISO/IEC 9796: Signieren Redundanz Message Verwendet wird eine Shadow. Funktion S Auffüllen S(a b) = π(a) π(b) Erweiterung Redundanz π 0 1 2 3 4 5 6 7 8 9 A B C D E F E 3 5 8 9 4 2 F 0 D B 6 7 A C 1 man erhält die 2 t-Byte-Folge MR = S(MEt) MEt S(MEt-1) MEt-1. . . S(ME 1) M zuletzt wird das Byte S(MEz) durch r S(MEz) ersetzt. ME = MEt-1 … ME 2 ME 1 Signatur Folie 10

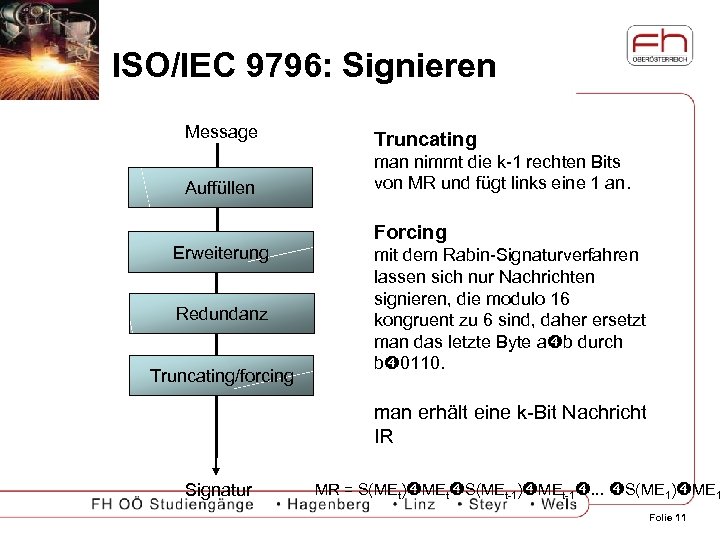ISO/IEC 9796: Signieren Message Truncating Auffüllen man nimmt die k-1 rechten Bits von MR und fügt links eine 1 an. Erweiterung Redundanz Truncating/forcing Forcing mit dem Rabin-Signaturverfahren lassen sich nur Nachrichten signieren, die modulo 16 kongruent zu 6 sind, daher ersetzt man das letzte Byte a b durch b 0110. man erhält eine k-Bit Nachricht IR Signatur MR = S(MEt) MEt S(MEt-1) MEt-1. . . S(ME 1) ME 1 Folie 11

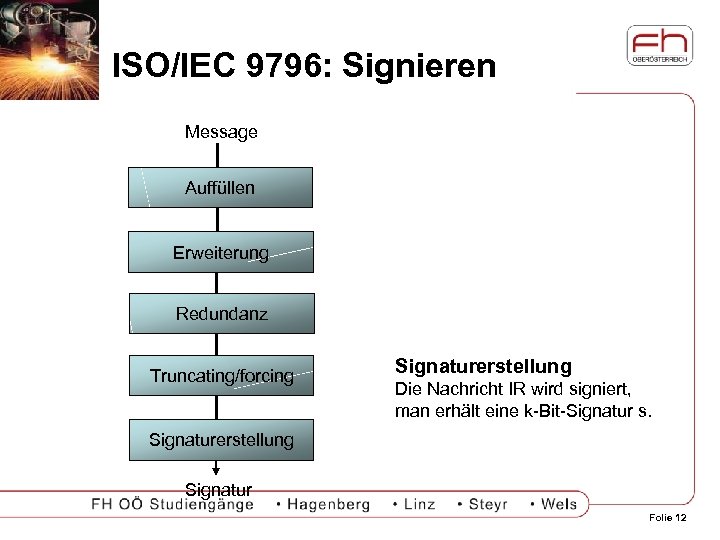ISO/IEC 9796: Signieren Message Auffüllen Erweiterung Redundanz Truncating/forcing Signaturerstellung Die Nachricht IR wird signiert, man erhält eine k-Bit-Signatur s. Signaturerstellung Signatur Folie 12

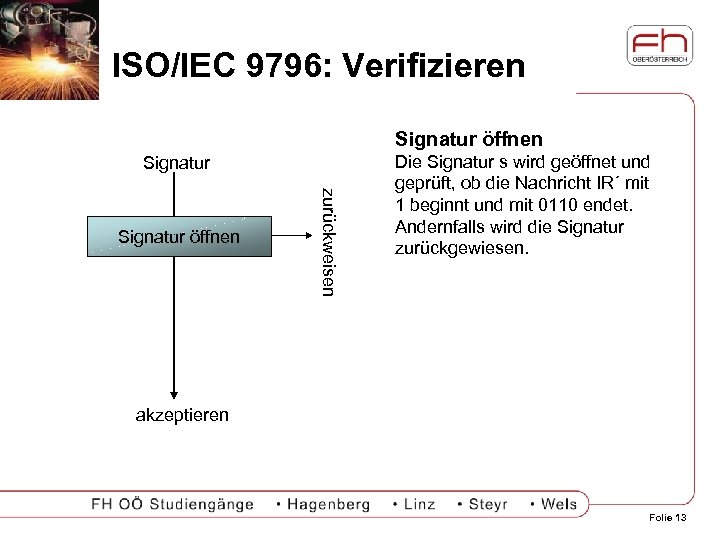ISO/IEC 9796: Verifizieren Signatur öffnen Signatur zurückweisen Signatur öffnen Die Signatur s wird geöffnet und geprüft, ob die Nachricht IR´ mit 1 beginnt und mit 0110 endet. Andernfalls wird die Signatur zurückgewiesen. akzeptieren Folie 13

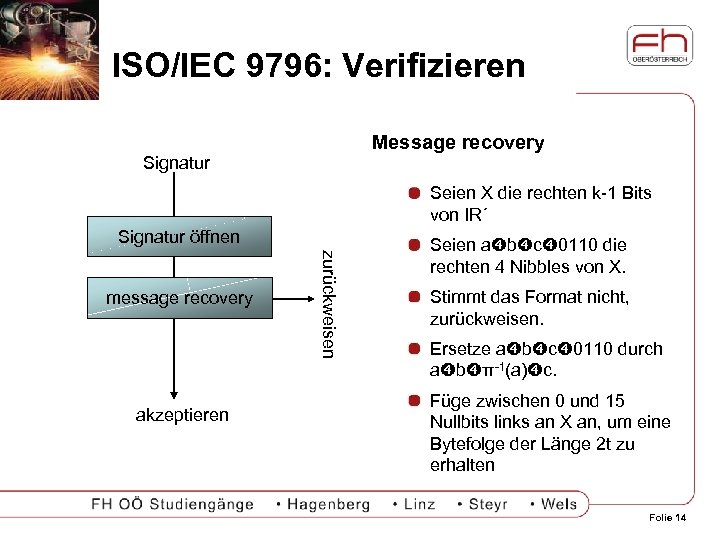ISO/IEC 9796: Verifizieren Message recovery Signatur Seien X die rechten k-1 Bits von IR´ Signatur öffnen akzeptieren zurückweisen message recovery Seien a b c 0110 die rechten 4 Nibbles von X. Stimmt das Format nicht, zurückweisen. Ersetze a b c 0110 durch a b π-1(a) c. Füge zwischen 0 und 15 Nullbits links an X an, um eine Bytefolge der Länge 2 t zu erhalten Folie 14

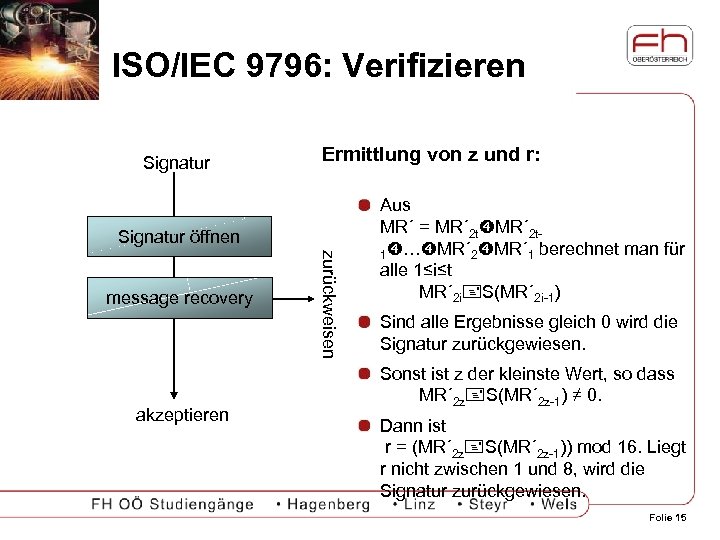ISO/IEC 9796: Verifizieren Signatur Ermittlung von z und r: Signatur öffnen akzeptieren zurückweisen message recovery Aus MR´ = MR´ 2 t 1 … MR´ 2 MR´ 1 berechnet man für alle 1≤i≤t MR´ 2 i S(MR´ 2 i-1) Sind alle Ergebnisse gleich 0 wird die Signatur zurückgewiesen. Sonst ist z der kleinste Wert, so dass MR´ 2 z S(MR´ 2 z-1) ≠ 0. Dann ist r = (MR´ 2 z S(MR´ 2 z-1)) mod 16. Liegt r nicht zwischen 1 und 8, wird die Signatur zurückgewiesen. Folie 15

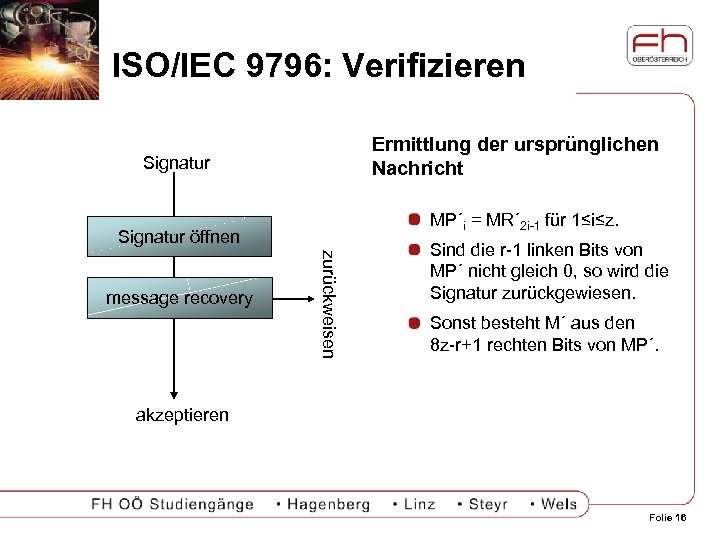ISO/IEC 9796: Verifizieren Ermittlung der ursprünglichen Nachricht Signatur MP´i = MR´ 2 i-1 für 1≤i≤z. Signatur öffnen zurückweisen message recovery Sind die r-1 linken Bits von MP´ nicht gleich 0, so wird die Signatur zurückgewiesen. Sonst besteht M´ aus den 8 z-r+1 rechten Bits von MP´. akzeptieren Folie 16

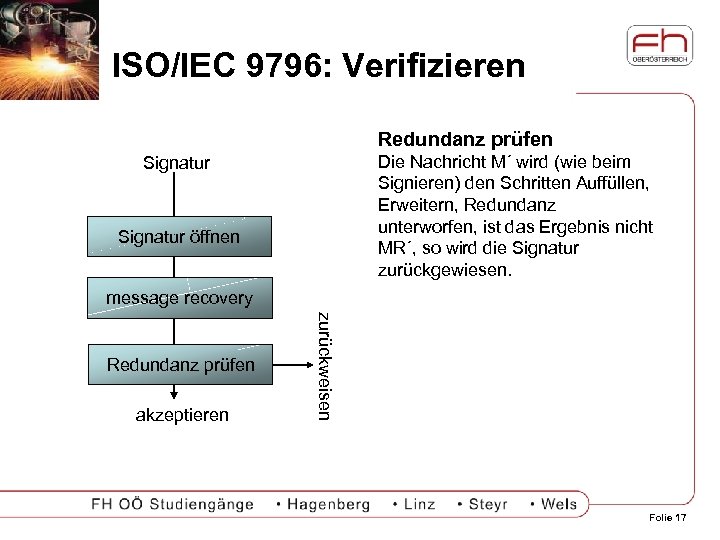ISO/IEC 9796: Verifizieren Redundanz prüfen Die Nachricht M´ wird (wie beim Signieren) den Schritten Auffüllen, Erweitern, Redundanz unterworfen, ist das Ergebnis nicht MR´, so wird die Signatur zurückgewiesen. Signatur öffnen message recovery akzeptieren zurückweisen Redundanz prüfen Folie 17

RSA-Signaturen ohne message recovery PKCS Public Key Cryptography Standards RSA Laboratories ab 1991 PKCS #1 RSA Cryptography Standard andere: #3: DH-Key Agreement Standard #6: Extended-Certificate Syntax Standard #12: Personal Information Exchange Syntax Standard #13: Elliptic Curve Cryptography Standard … Folie 18

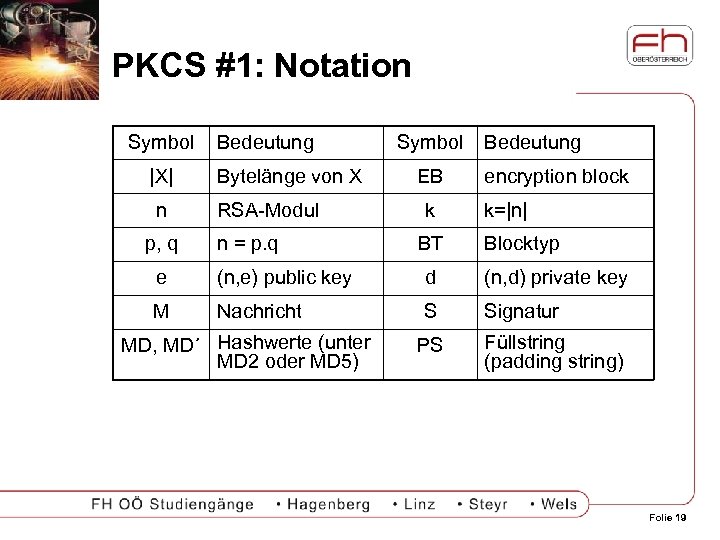PKCS #1: Notation Symbol |X| n p, q Bedeutung Bytelänge von X RSA-Modul n = p. q Symbol EB k BT Bedeutung encryption block k=|n| Blocktyp e (n, e) public key d (n, d) private key M Nachricht S Signatur MD, MD´ Hashwerte (unter MD 2 oder MD 5) PS Füllstring (padding string) Folie 19

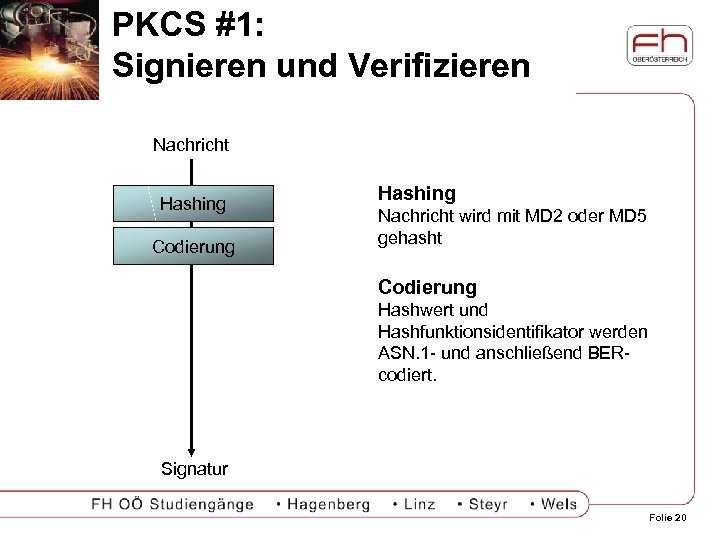PKCS #1: Signieren und Verifizieren Nachricht Hashing Codierung Hashing Nachricht wird mit MD 2 oder MD 5 gehasht Codierung Hashwert und Hashfunktionsidentifikator werden ASN. 1 - und anschließend BERcodiert. Signatur Folie 20

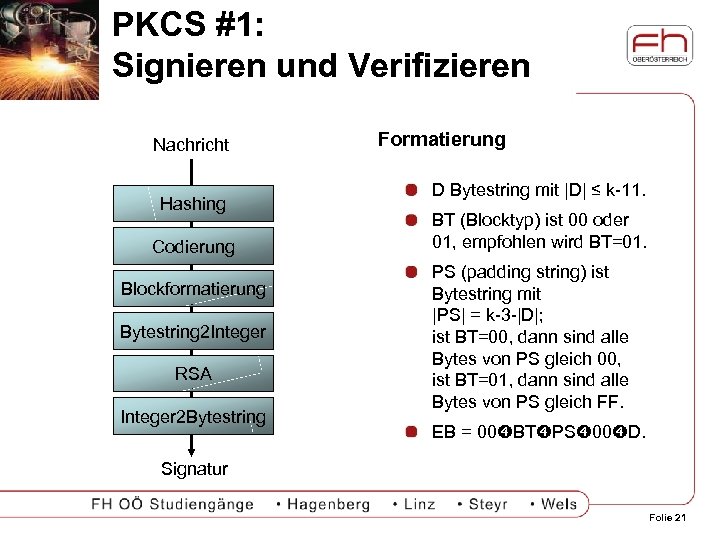PKCS #1: Signieren und Verifizieren Nachricht Hashing Codierung Blockformatierung Bytestring 2 Integer RSA Integer 2 Bytestring Formatierung D Bytestring mit |D| ≤ k-11. BT (Blocktyp) ist 00 oder 01, empfohlen wird BT=01. PS (padding string) ist Bytestring mit |PS| = k-3 -|D|; ist BT=00, dann sind alle Bytes von PS gleich 00, ist BT=01, dann sind alle Bytes von PS gleich FF. EB = 00 BT PS 00 D. Signatur Folie 21

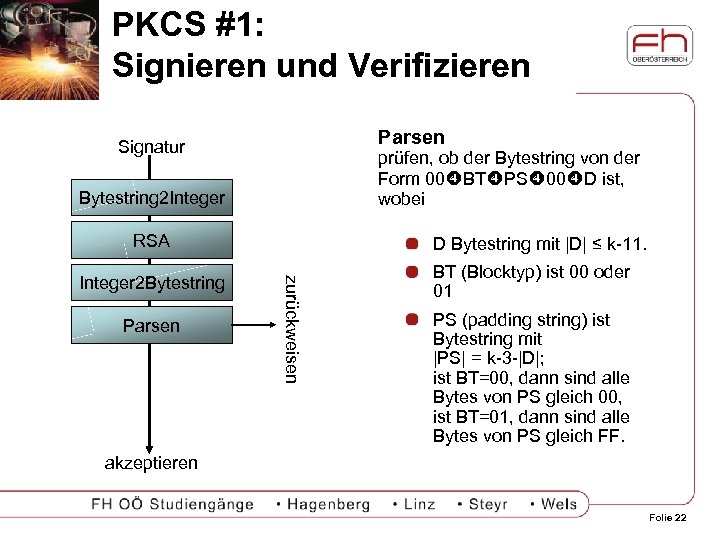PKCS #1: Signieren und Verifizieren Parsen Signatur prüfen, ob der Bytestring von der Form 00 BT PS 00 D ist, wobei Bytestring 2 Integer RSA Parsen zurückweisen Integer 2 Bytestring D Bytestring mit |D| ≤ k-11. BT (Blocktyp) ist 00 oder 01 PS (padding string) ist Bytestring mit |PS| = k-3 -|D|; ist BT=00, dann sind alle Bytes von PS gleich 00, ist BT=01, dann sind alle Bytes von PS gleich FF. akzeptieren Folie 22

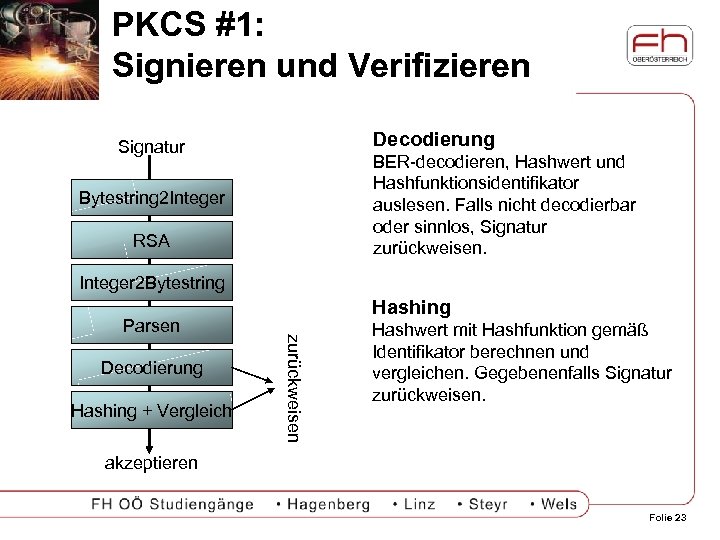PKCS #1: Signieren und Verifizieren Decodierung Signatur BER-decodieren, Hashwert und Hashfunktionsidentifikator auslesen. Falls nicht decodierbar oder sinnlos, Signatur zurückweisen. Bytestring 2 Integer RSA Integer 2 Bytestring Decodierung Hashing + Vergleich zurückweisen Parsen Hashing Hashwert mit Hashfunktion gemäß Identifikator berechnen und vergleichen. Gegebenenfalls Signatur zurückweisen. akzeptieren Folie 23

DSS • Digital Signature Standard • DSA (Digital Signature Algorithm) • FIPS 186 • Variante des El. Gamal-Signaturschemata • verwendete Hashfunktion ist SHA-1 Folie 24

DSS: Schlüsselerzeugung • Wähle q, so dass 2159 < q < 2160. • Wähle t, so dass 0 ≤ t < 8. Wähle t=8. • Wähle p prim, so dass gilt 2511+64 t < p < 2512+64 t und q | p-1. • Wähle ein Element g der Ordnung q in Zp*. • Wähle a zufällig, so dass 1 < a < q-1. • Berechne A = ga mod p. • Public key ist (p, q, g, A), secret key ist a. Folie 25

DSS: Signieren und Verifizieren Signieren: Wähle k zufällig, so dass 1 < k < q. Berechne r = (gk mod p) mod q. Berechne s = k-1(h(m)+ar) mod q. Signatur ist (r, s). Verifizieren: Prüfe 0 < r < q und 0 < s < q. Berechne x = s-1. h(m) mod q und y = r. s-1 mod q. Prüfe r = (gx. Ay mod p) mod q. Folie 26