Крива лінія як геометричне місце точок Крива

Крива лінія як геометричне місце точок.

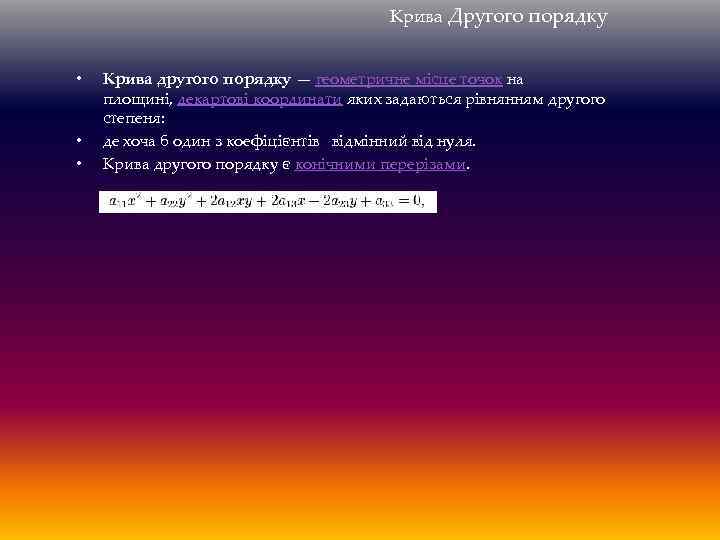Крива Другого порядку • • • Крива другого порядку — геометричне місце точок на площині, декартові координати яких задаються рівнянням другого степеня: де хоча б один з коефіцієнтів відмінний від нуля. Крива другого порядку є конічними перерізами.

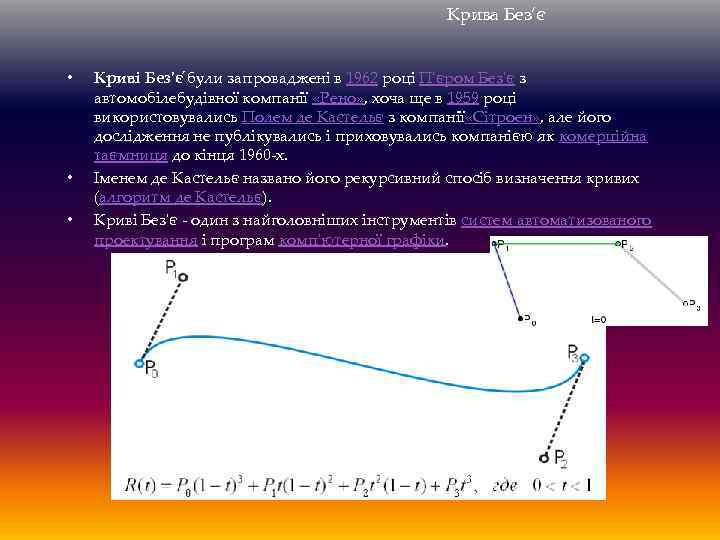Крива Без’є • • • Криві Без'є були запроваджені в 1962 році П'єром Без'є з автомобілебудівної компанії «Рено» , хоча ще в 1959 році використовувались Полем де Кастельє з компанії «Сітроен» , але його дослідження не публікувались і приховувались компанією як комерційна таємниця до кінця 1960 -х. Іменем де Кастельє названо його рекурсивний спосіб визначення кривих (алгоритм де Кастельє). Криві Без'є - один з найголовніших інструментів систем автоматизованого проектування і програм комп'ютерної графіки.

Фрактали. • Фракта л (лат. fractus — подрібнений, дробовий) — нерегулярна, самоподібна структура. В широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є подібними до неї самої. Термін фрактал увів 1975 року Бенуа Мандельброт.

Апроксима ція (лат. approximare — наближати) — наближене вираження одних математичних об'єктів іншими, простішими, наприклад, кривих ліній — ламаними, ірраціональних чисел — раціональними, неперервних функцій — многочленами. Апроксимації присвячені окремі розділи сучасної математики, наприклад, діофантові наближення — апроксимація ірраціональних чисел раціональними, наближення таінтерполяція функцій — апроксимація неперервних функцій алгебраїчними і тригонометричними многочленами.

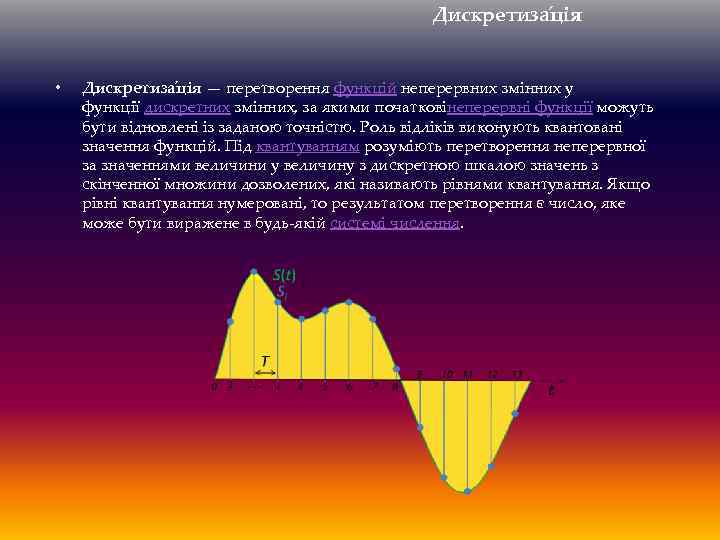Дискретиза ція • Дискретиза ція — перетворення функцій неперервних змінних у функції дискретних змінних, за якими початковінеперервні функції можуть бути відновлені із заданою точністю. Роль відліків виконують квантовані значення функцій. Під квантуванням розуміють перетворення неперервної за значеннями величини у величину з дискретною шкалою значень з скінченної множини дозволених, які називають рівнями квантування. Якщо рівні квантування нумеровані, то результатом перетворення є число, яке може бути виражене в будь-якій системі числення.

Інтерполяція • • Інтерполяція — в обчислювальній математиці спосіб знаходження проміжних значень величини за наявним дискретним набором відомих значень. Багатьом із тих, хто стикається з науковими та інженерними розрахунками часто доводиться оперувати наборами значень, отриманих експериментальним шляхом чи методом випадкової вибірки. Як правило, на підставі цих наборів потрібно побудувати функцію, зі значеннями якої могли б з високою точністю збігатися інші отримувані значення. Така задача називається апроксимацією кривої. Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних. Існує також близька до інтерполяції задача, що полягає в апроксимації якої-небудь складної функції іншою, простішою функцією. Якщо деяка функція занадто складна для продуктивних обчислень, можна спробувати обчислити її значення в декількох точках, а за ними побудувати, тобто інтерполювати, простішу функцію. Зрозуміло, використання спрощеної функції не дозволяє одержати такий ж точні результати, які давала б початкова функція. Але, для деяких класів задач, досягнутий виграш у простоті і швидкості обчислень може переважити отриманий огріх у результатах. Варто також згадати і зовсім інший різновид математичної інтерполяції, відому за назвою «інтерполяція операторів» . До класичних робіт з інтерполяції операторів відносяться теорема Рисса-Торина (Riesz-Thorin theorem) і теорема Марцинкевича (Marcinkiewicz theorem), що є основою для багатьох інших робіт.

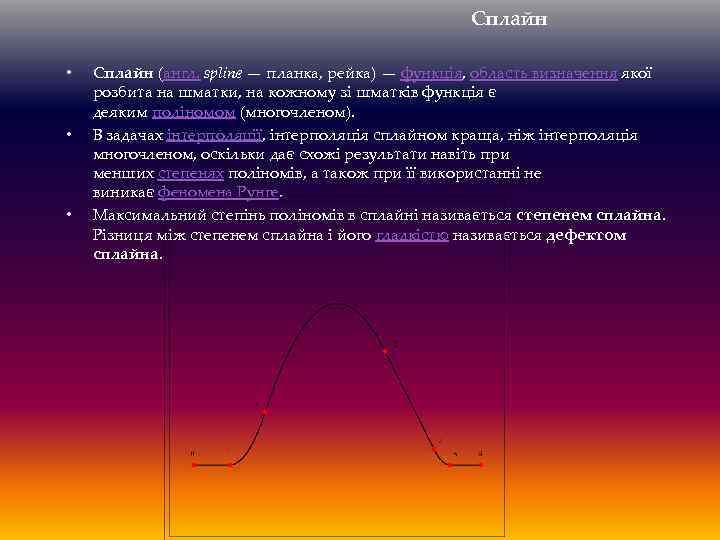Сплайн • • • Сплайн (англ. spline — планка, рейка) — функція, область визначення якої розбита на шматки, на кожному зі шматків функція є деяким поліномом (многочленом). В задачах інтерполяції, інтерполяція сплайном краща, ніж інтерполяція многочленом, оскільки дає схожі результати навіть при менших степенях поліномів, а також при її використанні не виникає феномена Рунге. Максимальний степінь поліномів в сплайні називається степенем сплайна. Різниця між степенем сплайна і його гладкістю називається дефектом сплайна.

Супровідний тригранник Френе • Репер або тригранник Френе або Френе - Серре відомий також, як природний, супроводжуючий, супутній - ортонормований репер в тривимірному просторі, що виникає при вивченні бірегулярних кривих. Одиничні вектори , відповідно для дотичної, головної нормалі і бінормалі кривої, при русі вздовж кривої змінюються. При відповідному виборі напрямку цих векторів з визначення кривизни та кручення виходять формули: дотична бінормаль головна нормаль Тригранник Френе для гвинтової лінії

Супровідний тригранник Френе Якщо взяти в якості m площину, що проходить через точку кривої, то умова стику при а≥ 2 визначає стичну площину кривої (рис. 1). Двічі диференційована крива в кожній точці має дотичну площину. Вона або єдина, або будь-яка площина, що проходить через дотичну кривої, є стичною. Пряма, перпендикулярна дотичній і проходить через точку дотику, називається нормаллю до кривої. Площина, перпендикулярна дотичній в даній точці кривої, називається нормальною площиною. Площина, що містить дотичну і бінормаль називається спрямляючою. Нормаль - це пряма, ортогональна (перпендикулярна) дотичний простір (дотичної прямої до кривої, дотичної площини до поверхні і т. д. ). Дотична пряма - пряма, що проходить через точку кривої і збігається з нею в цій точці з точністю до першого порядку. Бінормаль - нормаль кривої двоякої кривизни, (перпендикулярна до двох елементів кривої).