Критерий χ2 Пирсона q q Сопоставление эмпирического распределения

Критерий χ2 Пирсона q q Сопоставление эмпирического распределения с равномерным в Excel Сопоставление эмпирического распределения с нормальным в STATISTICA Сопоставление двух эмпирических распределений в Excel

Критерий 2 (критерий Пирсона) Эмпирическое значение критерия: где nэмп - наблюдаемые (эмпирические) частоты, nтеор - предполагаемые (теоретические) частоты, k – количество разрядов признака Число степеней свободы df=k-r-1, где r — число оцениваемых параметров закона распределения

Критерий 2 (критерий Пирсона) Эмпирическое значение критерия: где n – объем первой выборки, m- объем второй выборки, xi и yi – варианты первой и второй выборки Число степеней свободы df=(k-1)·(с-1), где k — число строк, с – число столбцов

Критерий 2 (критерий Пирсона) • Гипотезы для сравнения эмпирического и теоретического распределений: Н 0: полученное эмпирическое распределение признака не отличается от теоретического распределения Н 1: полученное эмпирическое распределение признака отличается от теоретического распределения • Гипотезы для сравнения двух эмпирических распределений: Н 0: эмпирическое распределение 1 не отличается от эмпирического распределения 2 Н 1: эмпирическое распределение 1 отличается от эмпирического распределения 2 Подчеркнутые слова заменить на соответствующие решаемой задаче формулировки

Критерий 2 (критерий Пирсона) Если то нулевая гипотеза принимается Если то нулевая гипотеза отклоняется Ограничения критерия: • объем выборки должен быть достаточно большим, n≥ 30 • теоретические частоты должны быть не меньше 5

Сопоставление эмпирического распределения с равномерным в Excel Пример Результаты контрольной работы: Оценки Количество оценок « 2» 14 « 3» « 4» « 5» 5 8 5 Гипотезы: Н 0: «Распределение оценок по контрольной работе не отличается от равномерного распределения» Н 1: «Распределение оценок по контрольной работе отличается от равномерного распределения»

Сопоставление эмпирического распределения с равномерным в Excel 1) Занести частоты эмпирического распределения в первый столбец Найти объем выборки (как сумму эмпирических частот) и проверить, больше ли он 30

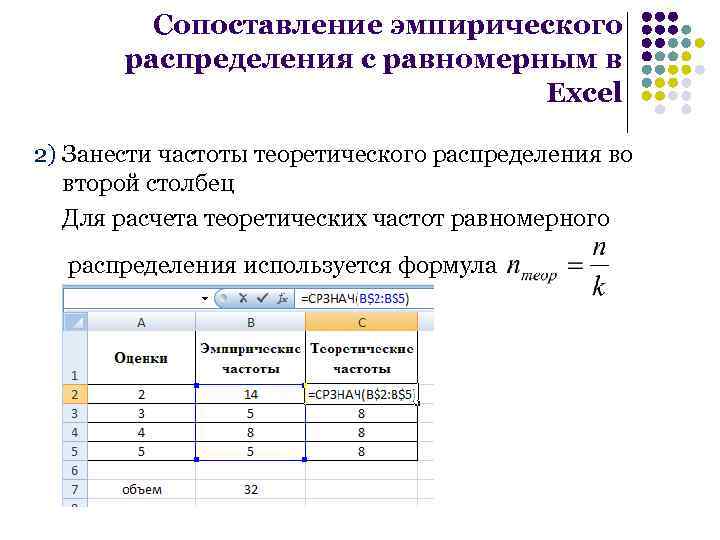Сопоставление эмпирического распределения с равномерным в Excel 2) Занести частоты теоретического распределения во второй столбец Для расчета теоретических частот равномерного распределения используется формула

Сопоставление эмпирического распределения с равномерным в Excel 3) Подсчитать уровень значимости p с помощью функции ХИ 2 ТЕСТ, указав в качестве фактического интервала – эмпирические частоты ожидаемого интервала – теоретические частоты

Сопоставление эмпирического распределения с равномерным в Excel 4) Сравнить уровень значимости p с уровнем значимости α если уровень значимости p>α, то гипотеза H 0 принимается если уровень значимости p≤α, то гипотеза H 0 отклоняется

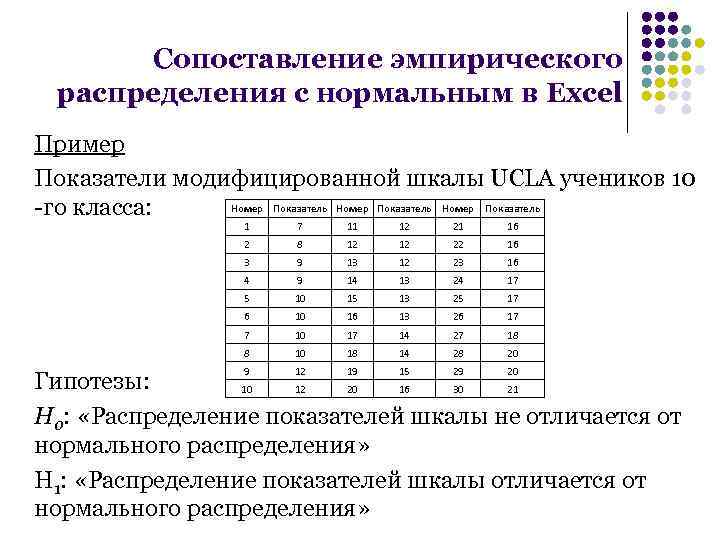Сопоставление эмпирического распределения с нормальным в Excel Пример Показатели модифицированной шкалы UCLA учеников 10 Номер Показатель -го класса: 1 7 11 12 21 16 2 8 12 12 22 16 3 9 13 12 23 16 4 9 14 13 24 17 5 10 15 13 25 17 6 10 16 13 26 17 7 10 17 14 27 18 8 10 18 14 28 20 9 12 19 15 29 20 Гипотезы: 10 12 20 16 30 21 Н 0: «Распределение показателей шкалы не отличается от нормального распределения» Н 1: «Распределение показателей шкалы отличается от нормального распределения»

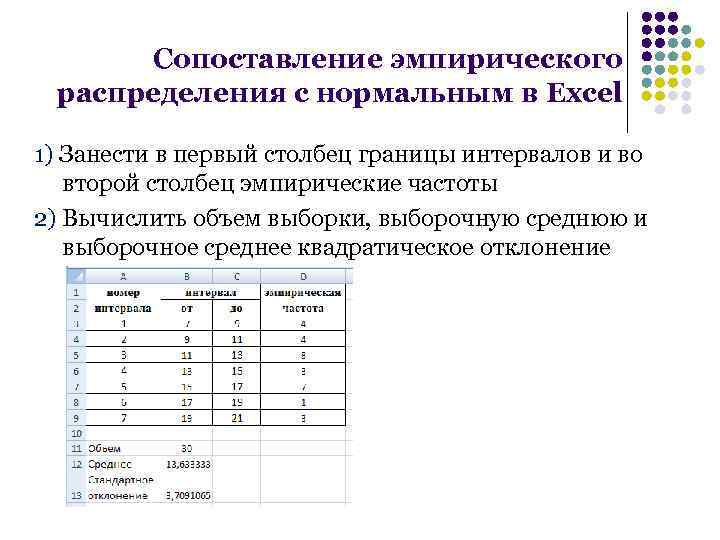Сопоставление эмпирического распределения с нормальным в Excel 1) Занести в первый столбец границы интервалов и во второй столбец эмпирические частоты 2) Вычислить объем выборки, выборочную среднюю и выборочное среднее квадратическое отклонение

Сопоставление эмпирического распределения с нормальным в Excel 3) Рассчитать теоретические частоты, т. е. частоты нормального распределения по формуле где Pi это вероятность попадания значения в i-й интервал Для этого: • для первого интервала

Сопоставление эмпирического распределения с нормальным в Excel при помощи критерия Пирсона Для этого: • для любого промежуточного интервала

Сопоставление эмпирического распределения с нормальным в Excel Для этого: • для последнего интервала

Сопоставление эмпирического распределения с нормальным в Excel 4) При необходимости объединить интервалы, для которых теоретические частоты оказались меньше 5

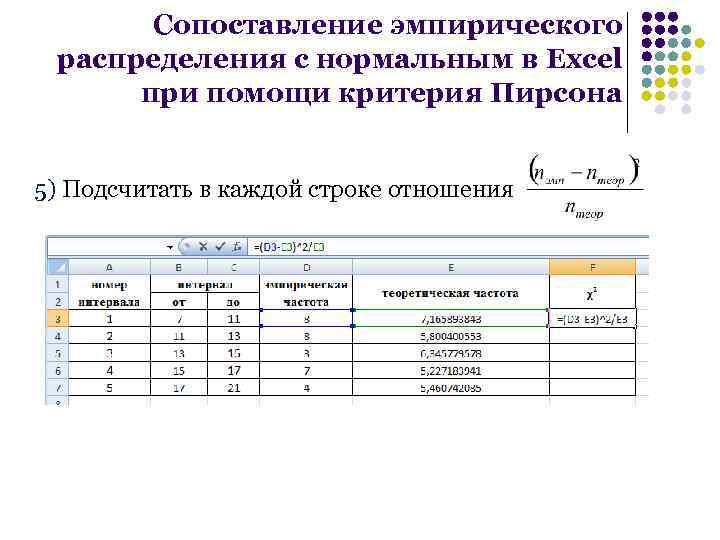Сопоставление эмпирического распределения с нормальным в Excel при помощи критерия Пирсона 5) Подсчитать в каждой строке отношения

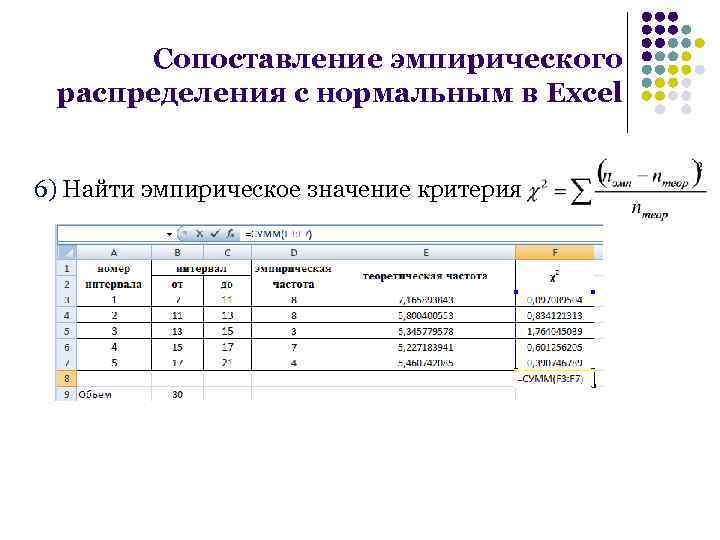Сопоставление эмпирического распределения с нормальным в Excel 6) Найти эмпирическое значение критерия

Сопоставление эмпирического распределения с нормальным в Excel 7) Определить уровень значимости p при помощи функции ХИ 2 РАСП

Сопоставление эмпирического распределения с нормальным в Excel 8) Сравнить уровень значимости p с уровнем значимости α если уровень значимости p>α, то гипотеза H 0 принимается если уровень значимости p≤α, то гипотеза H 0 отклоняется

Сопоставление эмпирического распределения с нормальным в STATISTICA 1) Занести показатели 2) Найти минимальное и максимальное значения признака Определить, на какое количество интервалов будут разбиваться значения

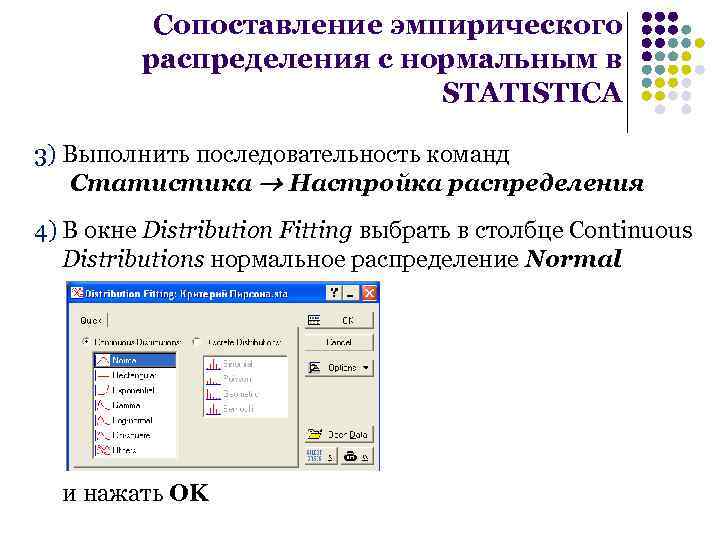Сопоставление эмпирического распределения с нормальным в STATISTICA 3) Выполнить последовательность команд Статистика Настройка распределения 4) В окне Distribution Fitting выбрать в столбце Continuous Distributions нормальное распределение Normal и нажать OK

Сопоставление эмпирического распределения с нормальным в STATISTICA 5) Нажать кнопку Variable и выбрать нужную переменную 6) На вкладке Parameters указать количество интервалов (Number of categories) минимум (Lower Limit) максимум (Upper Limit)

Сопоставление эмпирического распределения с нормальным в STATISTICA 7) На вкладке Options установить флажок в поле Combine Categories и нажать Summary

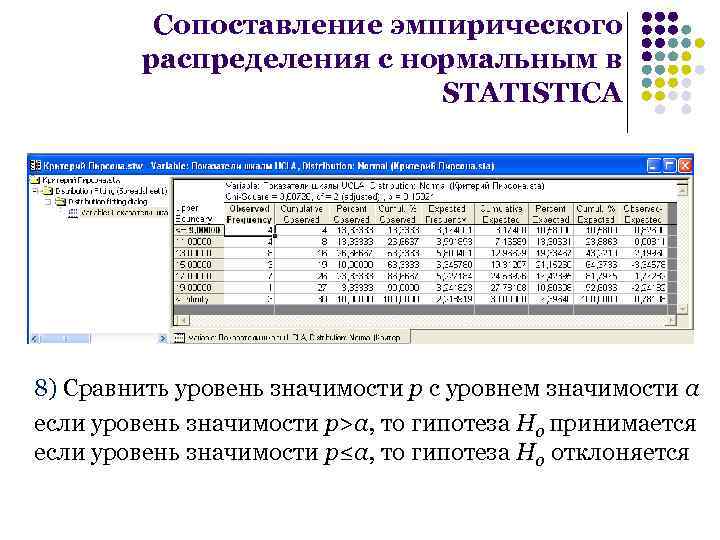Сопоставление эмпирического распределения с нормальным в STATISTICA 8) Сравнить уровень значимости p с уровнем значимости α если уровень значимости p>α, то гипотеза H 0 принимается если уровень значимости p≤α, то гипотеза H 0 отклоняется

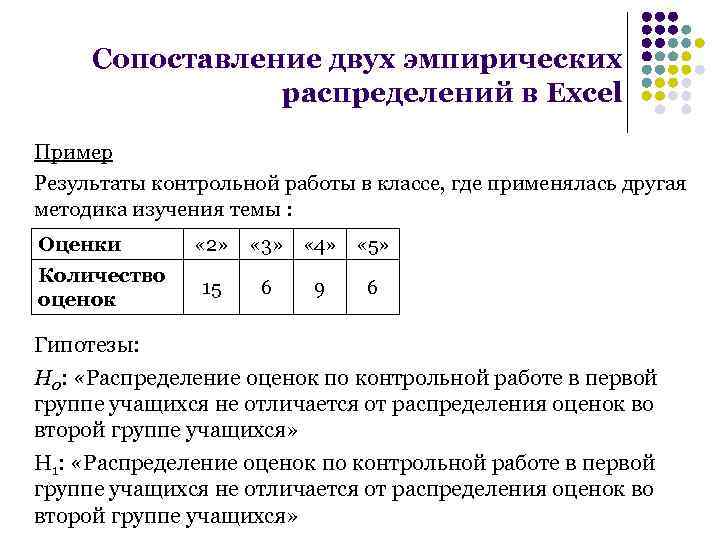Сопоставление двух эмпирических распределений в Excel Пример Результаты контрольной работы в классе, где применялась другая методика изучения темы : Оценки Количество оценок « 2» 15 « 3» « 4» « 5» 6 9 6 Гипотезы: Н 0: «Распределение оценок по контрольной работе в первой группе учащихся не отличается от распределения оценок во второй группе учащихся» Н 1: «Распределение оценок по контрольной работе в первой группе учащихся не отличается от распределения оценок во второй группе учащихся»

Сопоставление двух эмпирических распределений в Excel 1) Занести эмпирические частоты в первый и второй столбец

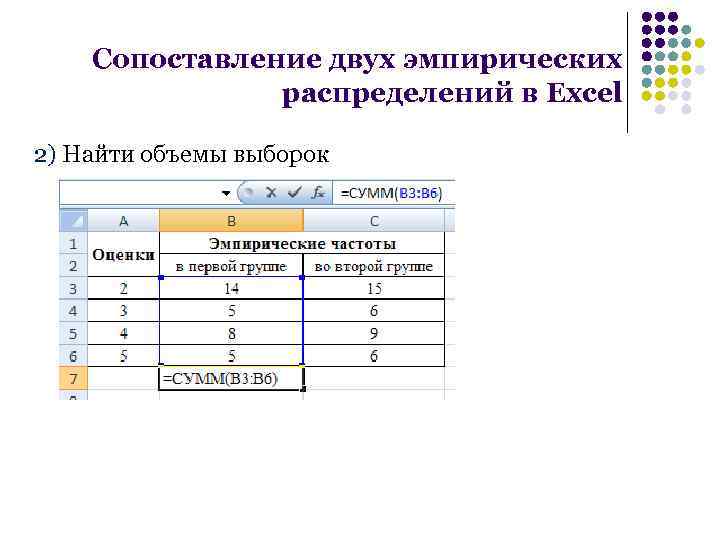Сопоставление двух эмпирических распределений в Excel 2) Найти объемы выборок

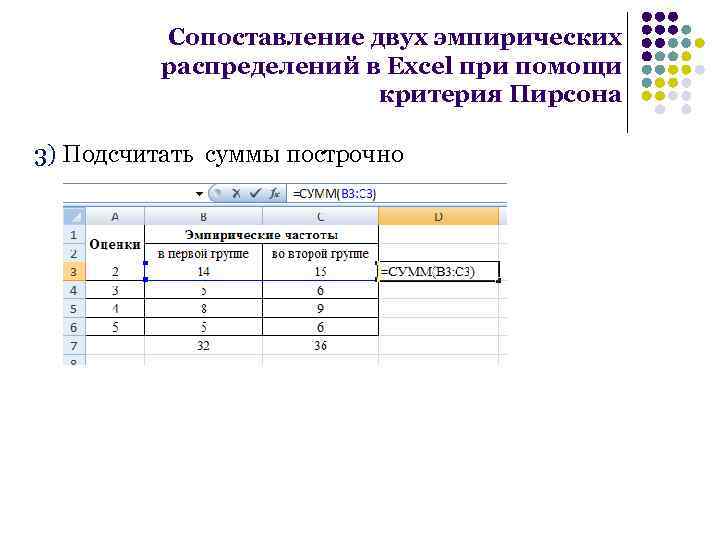Сопоставление двух эмпирических распределений в Excel при помощи критерия Пирсона 3) Подсчитать суммы построчно

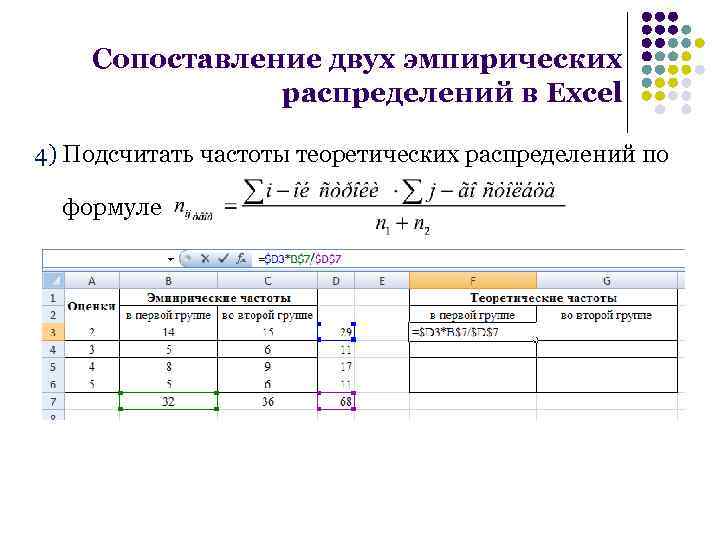Сопоставление двух эмпирических распределений в Excel 4) Подсчитать частоты теоретических распределений по формуле

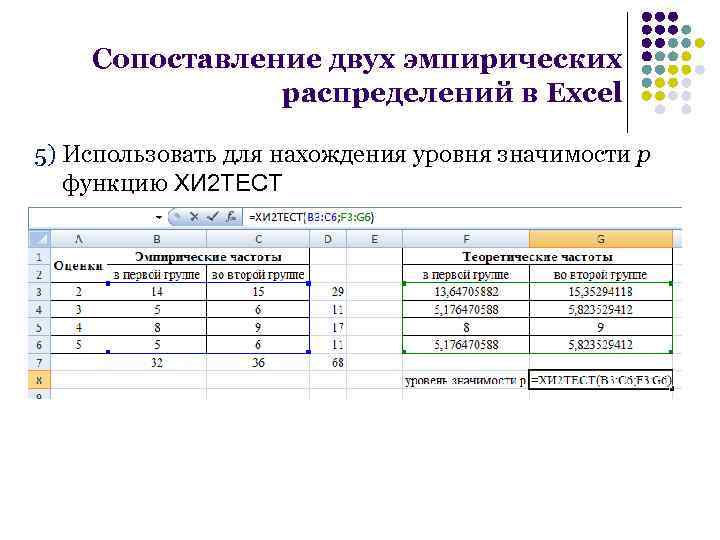Сопоставление двух эмпирических распределений в Excel 5) Использовать для нахождения уровня значимости p функцию ХИ 2 ТЕСТ

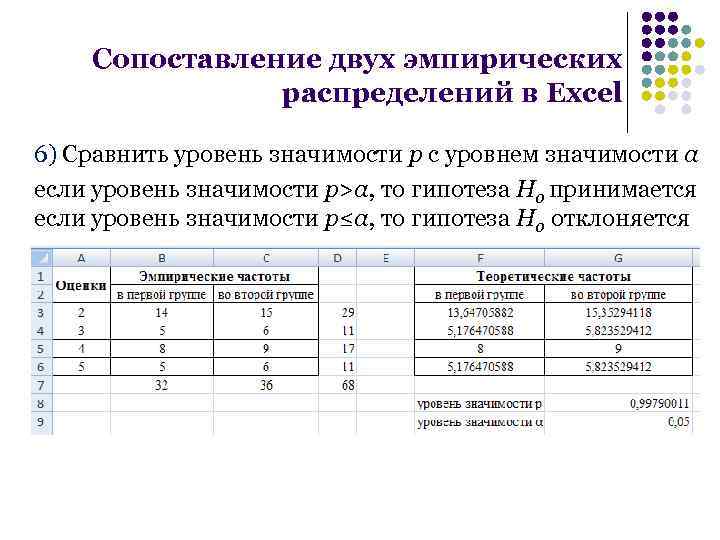Сопоставление двух эмпирических распределений в Excel 6) Сравнить уровень значимости p с уровнем значимости α если уровень значимости p>α, то гипотеза H 0 принимается если уровень значимости p≤α, то гипотеза H 0 отклоняется

Критерий 2 (критерий Пирсона) Примечание. В случае если число степеней свободы df=1, то необходимо внести в критерий поправку на непрерывность: перед возведением в квадрат разности эмпирических и теоретических частот необходимо уменьшить абсолютную величину этой разности на 0, 5

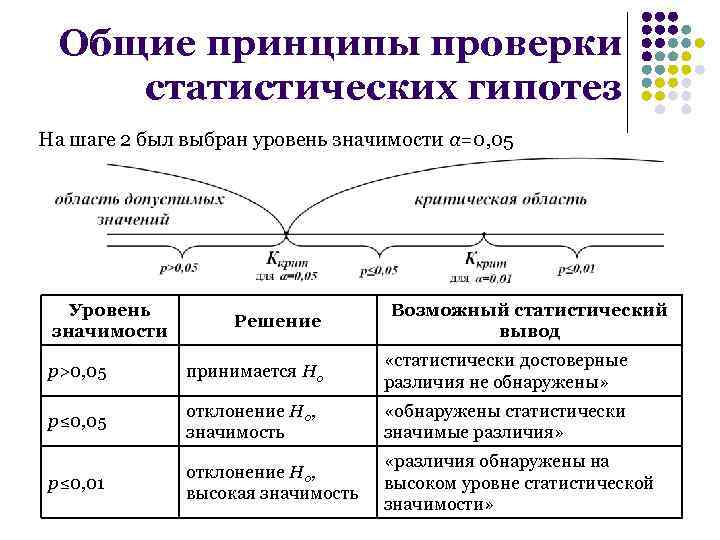Общие принципы проверки статистических гипотез На шаге 2 был выбран уровень значимости α=0, 05 Уровень значимости Решение Возможный статистический вывод p>0, 05 принимается H 0 «статистически достоверные различия не обнаружены» p≤ 0, 05 отклонение H 0, значимость «обнаружены статистически значимые различия» p≤ 0, 01 отклонение H 0, высокая значимость «различия обнаружены на высоком уровне статистической значимости»