КРИТЕРИИ ДОСТОВЕРНОСТИ ОЦЕНОК

КРИТЕРИИ ДОСТОВЕРНОСТИ ОЦЕНОК

t-Критерий Стьюдента ( t- распределение) Использование формулы Гаусса-Лапласа для сравнительной оценки средних величин затруднено тем, что в качестве аргументов в эту формулу входят генеральные параметры и (которые, как правило, ос таются неизвестными), тогда сравнении выборочных групп приходится пользоваться не генеральными, а выборочными характеристиками x и. Учитывая это обстоятельство, английский математик В. Госсет, в 1908 г. нашел закон распределения величины , в которой генеральный параметр заменен на его выборочную характеристику , т. е. нашел закон распределения значений

Оказалось, что отношение разности между выборочной и генераль ной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле: f(t)= для где С - константа, зависящая только от числа степеней свободы k = n - 1.

Открытый Госсетом и теоретически обоснованный Р. Фишером закон t-распределения служит основой так называемой теории , малой вы борки которая характеризует распределение выборочных средних в нор распределяющейся совокупности в мально зависимости от объема выбор ки, t-распределение зависит только от числа степеней свободы k = п - 1, причем с увеличением объема выборки n t- распределение быстро прибли жается к нормальному жается с параметрами = 0 и = 1 и уже при n > 30 не личается от него. Это видно из табл. 1, в которой от наряду с табулированны ми значениями фу нормального распределения приведены табулиро ванные значения для t-распределения разных значенийn.

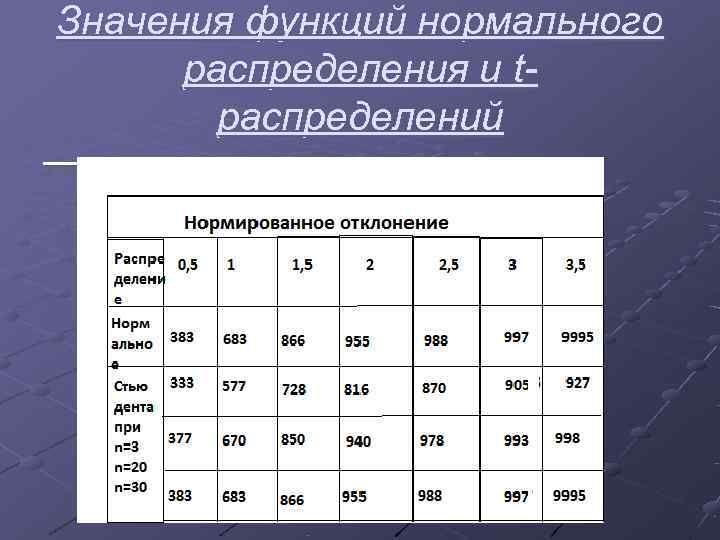Значения функций нормального распределения и t- распределений

Для выборок, объем которых превышает 30 единиц, величина t распределяется нормально и не зависит от числа наблюдений. Если же n < 30, характер t-распределения находится в зависимости от числа наблюденийn. Для практического использования t- распределения составлена спе циальная циальная таблица, в которой содержатся крити ческие ческие точки (ts) для разных уровней значимости а и чисел степеней свободы k.