Кристалографія Лекція 2 Кристал тверде тіло

Кристалографія Лекція 2

Кристал • тверде тіло, яке володіє трансляційною тримірно-періодичною атомною структурою і здатне самоогранятись в умовах вільного росту (коли росту не заважають сусідні кристали)

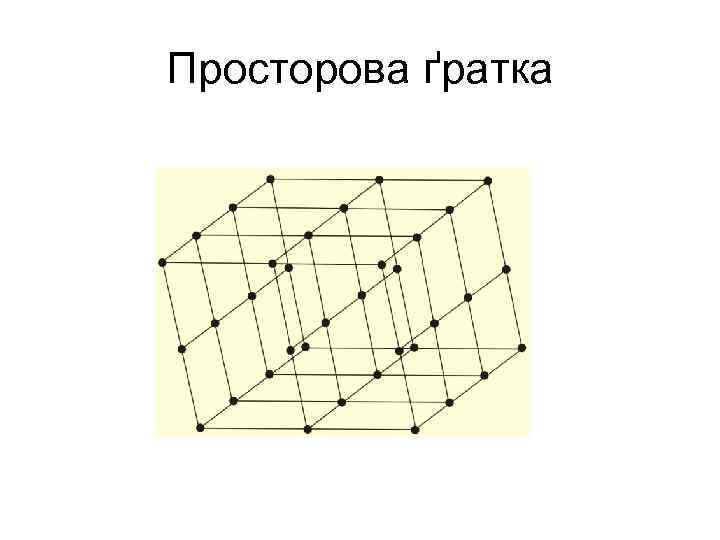Просторова ґратка

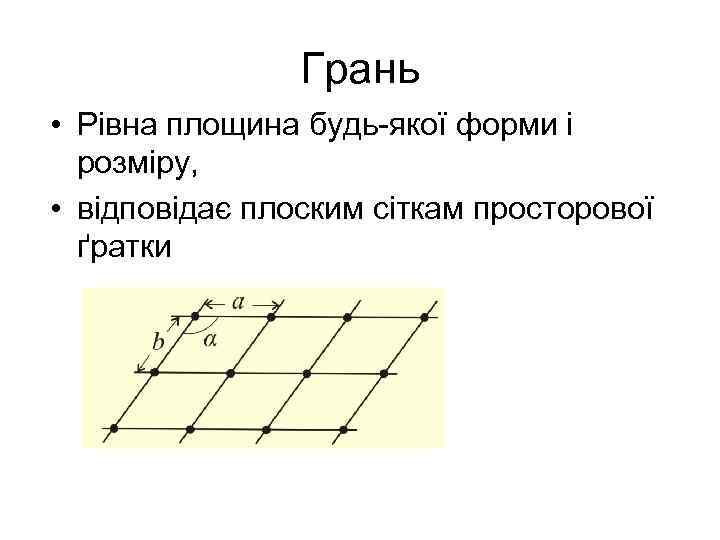Грань • Рівна площина будь-якої форми і розміру, • відповідає плоским сіткам просторової ґратки

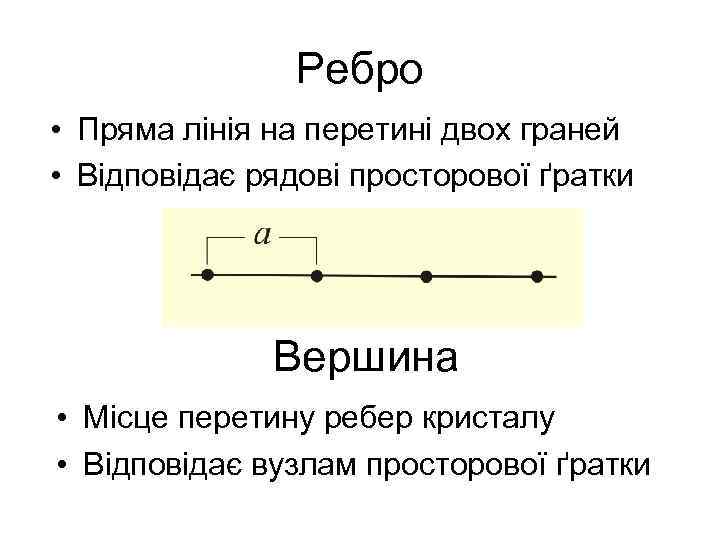Ребро • Пряма лінія на перетині двох граней • Відповідає рядові просторової ґратки Вершина • Місце перетину ребер кристалу • Відповідає вузлам просторової ґратки

Елементарний паралелепіпед (елементарна комірка) просторової ґратки: • а, b, c – проміжки рядів; α, β, γ – кути між осями

Найважливіші властивості кристалів • Здатності самоогранятись • Однорідність (будь-яких ділянках кристалічної речовини певного складу всі її властивості тотожні) • Анізотропія • Симетрія кристалічної речовини • Мінлива швидкість росту граней

Анізотропія Якщо є залежність властивостей від напрямку, то така залежність називається анізотропією • Деякі властивості кристалів скалярні, тобто не залежать від напрямку (питома вага, щільність, температура та ін. ). • В той же час багато властивостей, наприклад, теплопровідність, діелектрична і магнітна сприйнятливість, спайність, твердість, показник заломлення світла та інші, суттєво залежать від напрямку, стосовно якого вони визначені

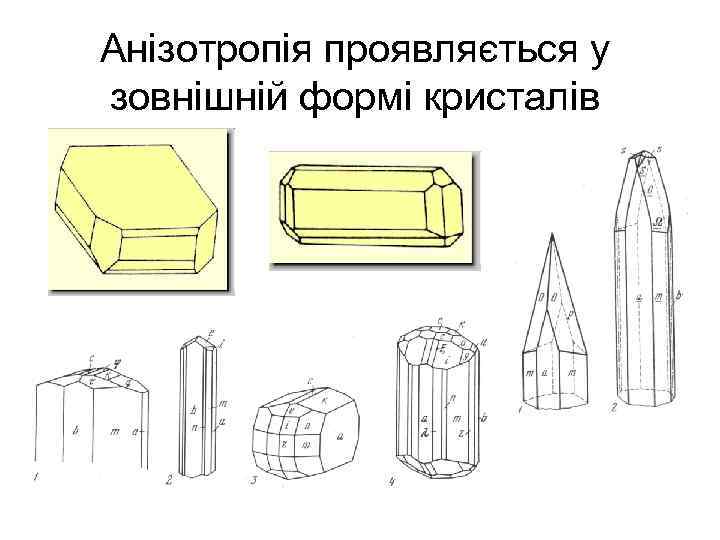Анізотропія проявляється у зовнішній формі кристалів

Енстатит Mg 2[Si 2 O 6]

Еґірин Na. Fe 3+[Si 2 O 6]

хромдіопсид (VICr 3+) Діопсид Ca. Mg[Si 2 O 6]

Видовжені кристали гюбнериту і кварцу

Сплющений обрис вульфеніту Pb[Mo. O 4]

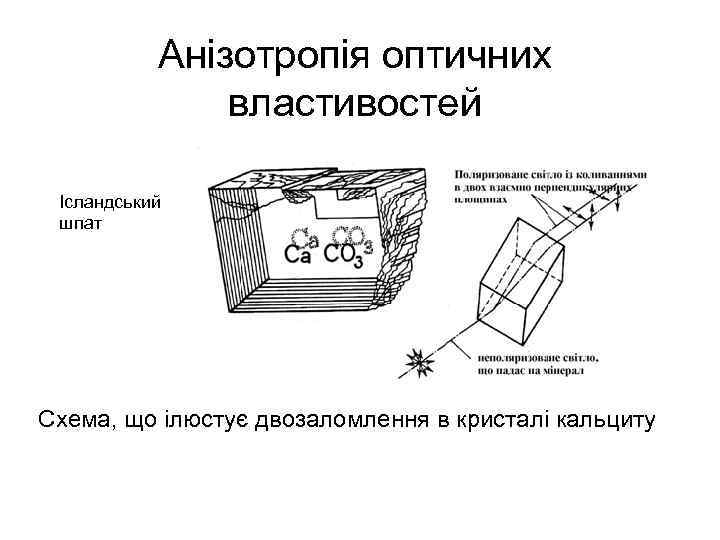Анізотропія оптичних властивостей Ісландський шпат Схема, що ілюстує двозаломлення в кристалі кальциту

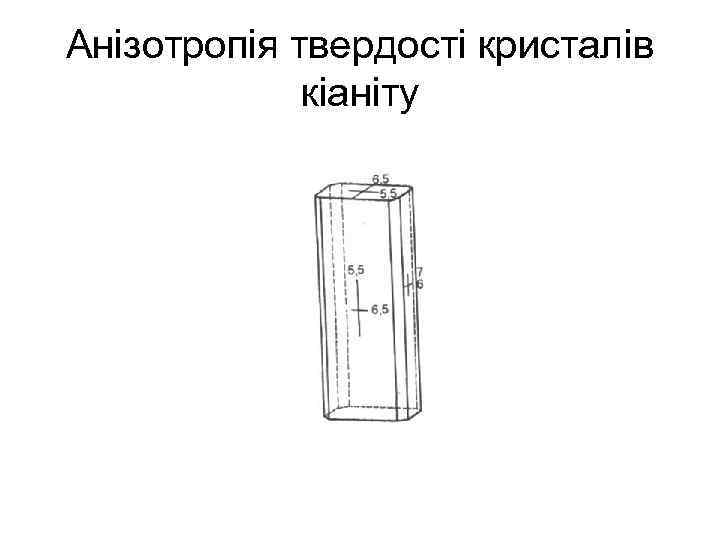Анізотропія твердості кристалів кіаніту

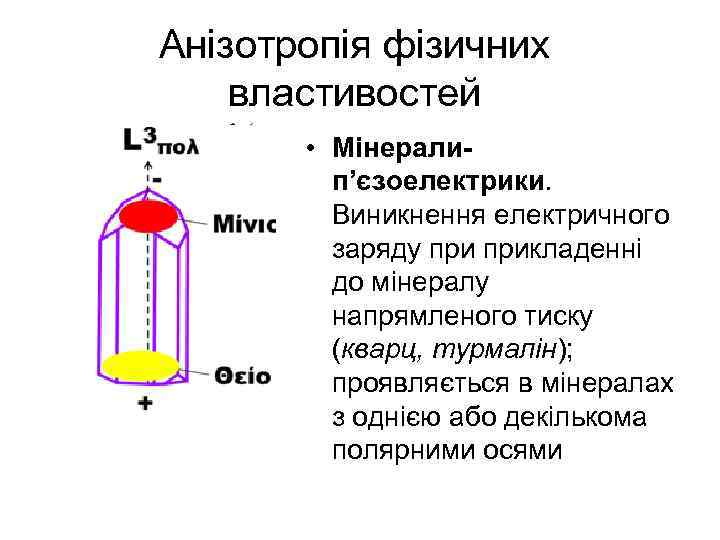Анізотропія фізичних властивостей • Мінералип’єзоелектрики. Виникнення електричного заряду прикладенні до мінералу напрямленого тиску (кварц, турмалін); проявляється в мінералах з однією або декількома полярними осями

Ізотропні речовини • Якщо властивість речовини не змінюється в залежності від напрямку, то говорять, що речовина ізотропна відносно цієї властивості • рідини й гази ізотропні відносно всіх властивостей, • кристали можуть бути ізотропними стосовно лише деяких властивостей • кристали кубічної сингонії оптично ізотропні, але механічні й інші властивості в різних напрямках у них проявляють анізотропію

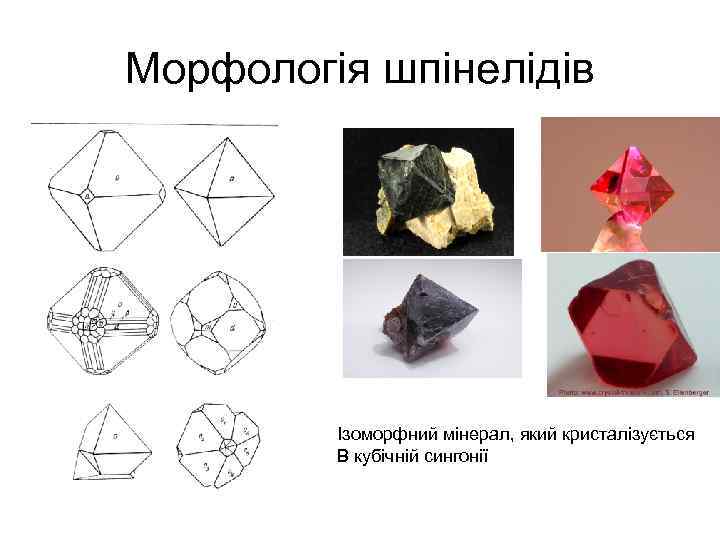Морфологія шпінелідів Ізоморфний мінерал, який кристалізується В кубічній сингонії

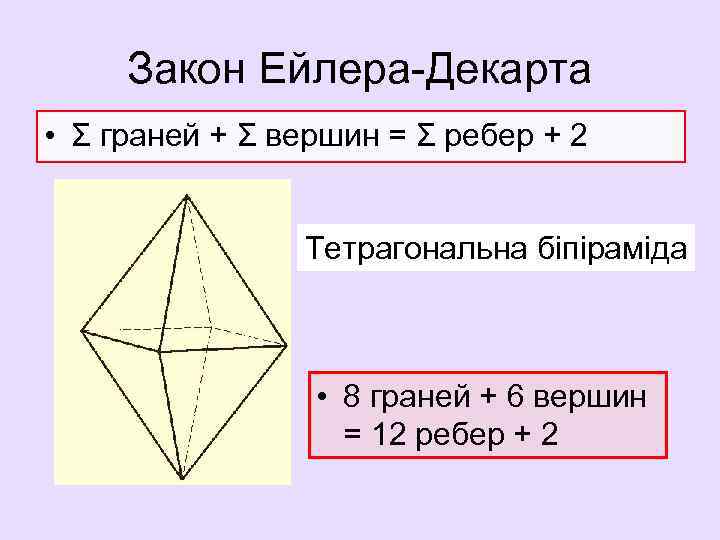Закон Ейлера-Декарта • Σ граней + Σ вершин = Σ ребер + 2 Тетрагональна біпіраміда • 8 граней + 6 вершин = 12 ребер + 2

Закон Браве – грані кристалів ростуть зі швидкостями, зворотньо пропорційними густині їхніх вузлових сіток – ретикулярній густині • Тому грані з малою ретикулярною щільністю швидко заростають і виклинюються, а грані густо усаджені атомами залишаються

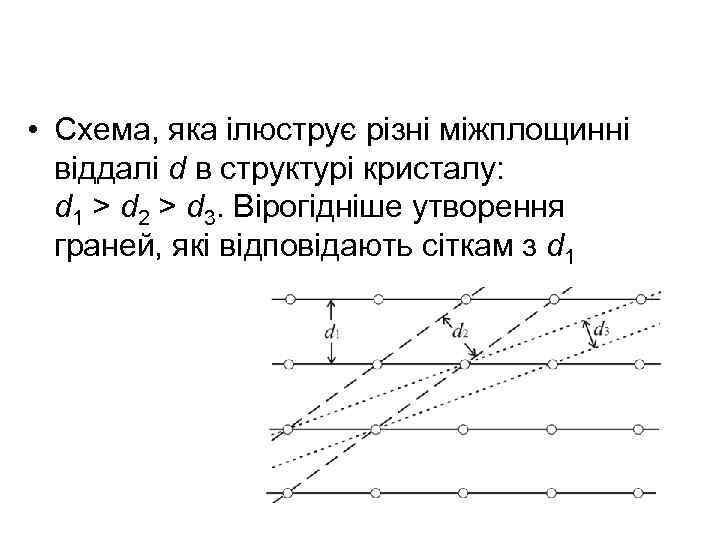• Схема, яка ілюструє різні міжплощинні віддалі d в структурі кристалу: d 1 > d 2 > d 3. Вірогідніше утворення граней, які відповідають сіткам з d 1

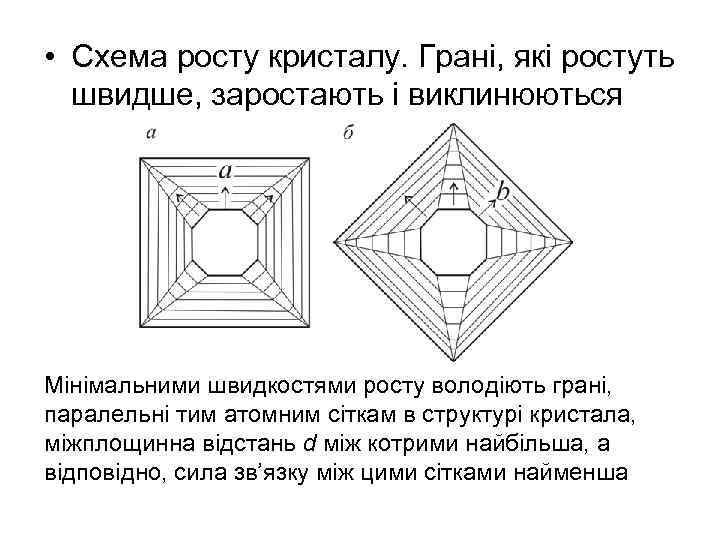• Схема росту кристалу. Грані, які ростуть швидше, заростають і виклинюються Мінімальними швидкостями росту володіють грані, паралельні тим атомним сіткам в структурі кристала, міжплощинна відстань d між котрими найбільша, а відповідно, сила зв’язку між цими сітками найменша

Інше формулювання закону Браве Кристал ограняється гранями з найбільшою ретикулярною густиною (це). Закон Кюрі-Вульфа В енергетичному плані реальні грані кристала відповідають плоским сіткам структури з мінімальною поверхневою енергією

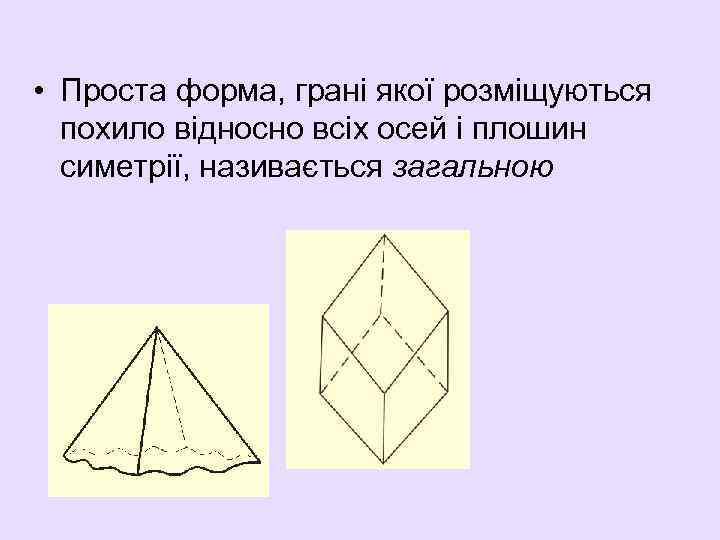• Проста форма, грані якої розміщуються похило відносно всіх осей і плошин симетрії, називається загальною

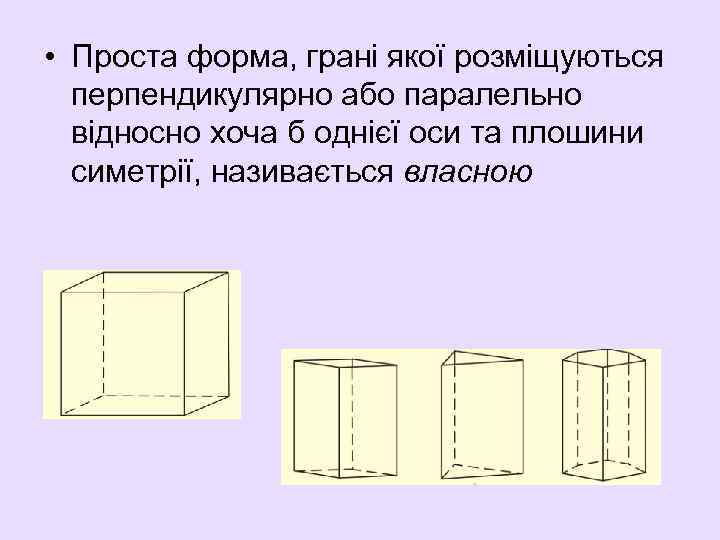• Проста форма, грані якої розміщуються перпендикулярно або паралельно відносно хоча б однієї оси та плошини симетрії, називається власною

• Поясом (або зоною) в геометрії багатогранників називається сукупність всіх граней, які перетинаються по паралельних ребрах • Можливою гранню або можливим ребром кристалу називають таку грань або ребро, котрі не присутні на даному кристалі, але можуть зустрінутись на інших кристалах тієї самої речовини

Морфологія ставроліту Ілюстрація можливих граней або можливих ребер

Закон зон Вейса • кожна площина, яка паралельна двом будь-яким дійсним або можливим ребрам кристалу – це можлива грань кристалу, а кожний напрям, паралельний лінії перетину двох будьяких дійсних або можливих граней кристалу – це можливе ребро кристалу

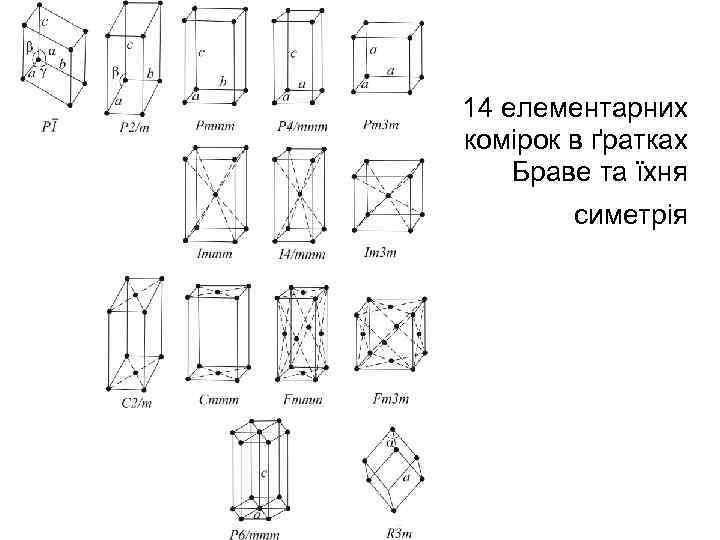14 елементарних комірок в ґратках Браве та їхня симетрія

14 тривимірних ґраток Браве • Закономірно розміщені в просторі точки у вигляді правильних паралелепіпедів з певними лінійними (a, b, c) і кутовими параметрами (α, β, γ)

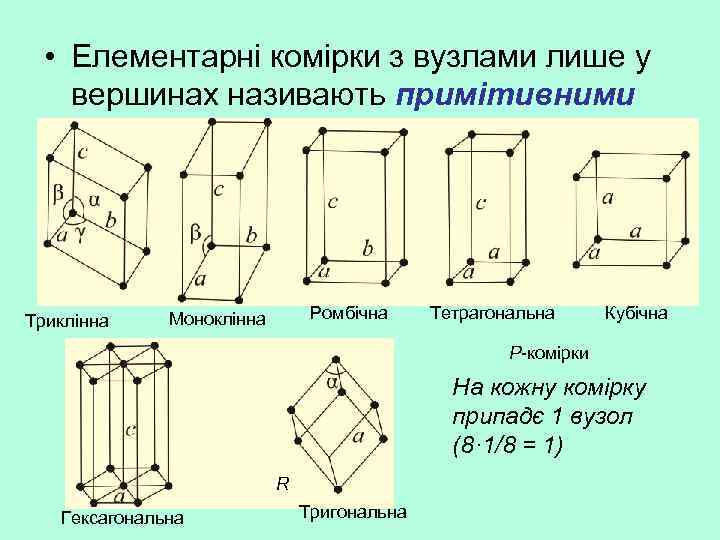• Елементарні комірки з вузлами лише у вершинах називають примітивними Триклінна Ромбічна Моноклінна Тетрагональна Кубічна Р-комірки На кожну комірку припадє 1 вузол (8· 1/8 = 1) R Гексагональна Тригональна

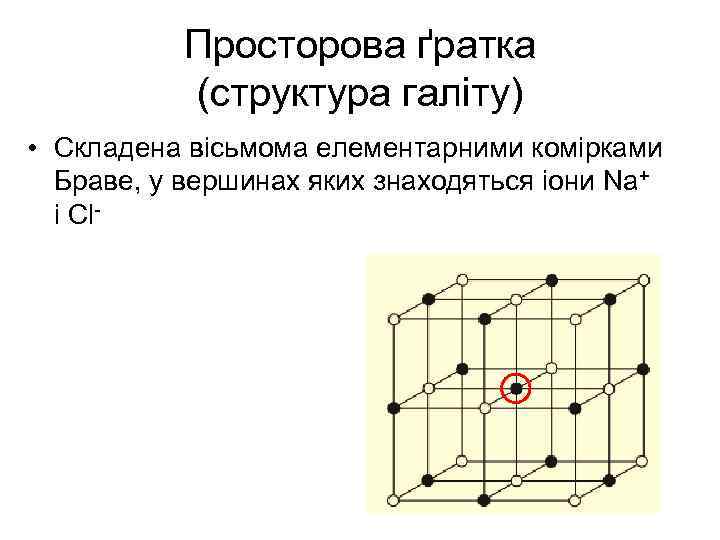Просторова ґратка (структура галіту) • Складена вісьмома елементарними комірками Браве, у вершинах яких знаходяться іони Na+ і Cl-

• Ґратки (з додатковими вузлами в центрі граней або в середині елементарної комірки) називають непримітивними Ø Базоцентровані Ø Об’ємноцентровані Ø Гранецентровані

Ø Базоцентровані – елементарні комірки, в яких атоми, іони чи молекули розміщені як у вершинах правильного паралелепіпеда, так і в центрі верхньої та нижньої плоских сіток На кожну комірку припадє 2 вузли (8· 1/8 + 2 · 1/2 = 2) С-комірки Моноклінна Ромбічна

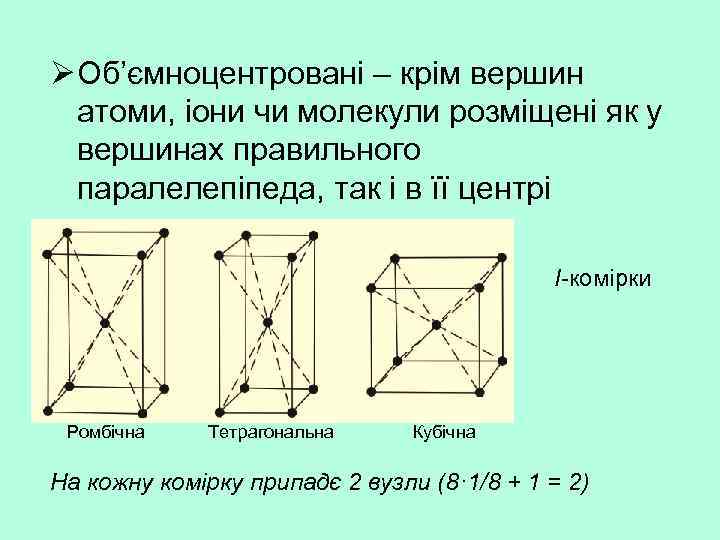Ø Об’ємноцентровані – крім вершин атоми, іони чи молекули розміщені як у вершинах правильного паралелепіпеда, так і в її центрі I-комірки Ромбічна Тетрагональна Кубічна На кожну комірку припадє 2 вузли (8· 1/8 + 1 = 2)

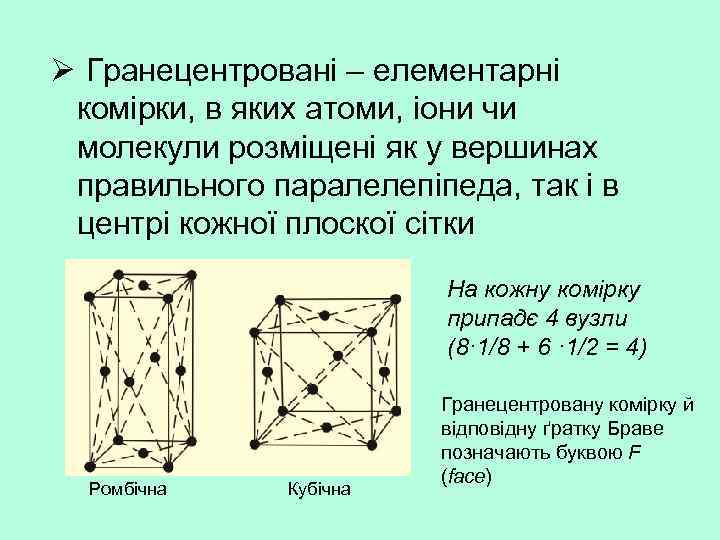Ø Гранецентровані – елементарні комірки, в яких атоми, іони чи молекули розміщені як у вершинах правильного паралелепіпеда, так і в центрі кожної плоскої сітки На кожну комірку припадє 4 вузли (8· 1/8 + 6 · 1/2 = 4) Ромбічна Кубічна Гранецентровану комірку й відповідну ґратку Браве позначають буквою F (face)

Фізичний зміст ґраток Браве • показують в структурах кристалів 14 варіантів розташування однотипних матеріальних частинок (з паралельною орієнтацією їх хімічних зв’язків і комплексу всіх оточуючих сусідів); • навіть найскладніші структури можна умовно розглядати як систему вставлених одна в одну однакових підґраток, які відповідають атомам кожного сорту

Елементи симетрії просторових граток • Поняття трансляція Т означає паралельний перенос (поступання) у даному напрямкові – періодичне переміщення у просторі окремих вузлів просторових ґраток і всієї структури

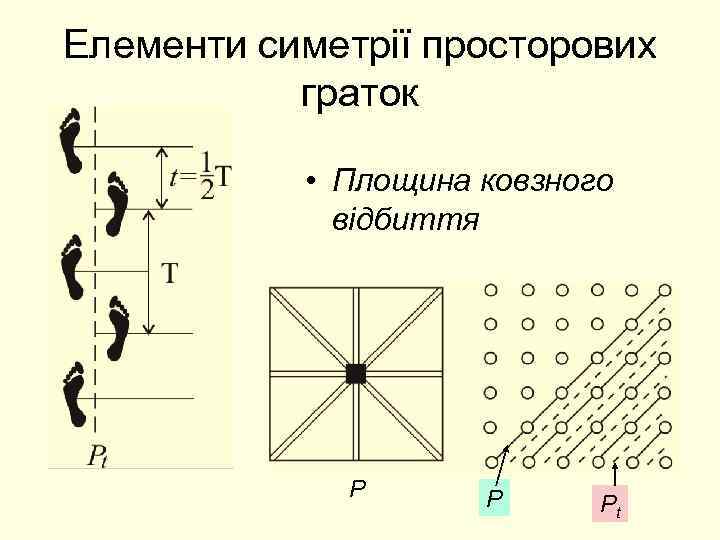Елементи симетрії просторових граток • Площина ковзного відбиття Р Р Рt

Гвинтові осі симетрії Lnt – елементи симетрії лише нескінчених фігур (просторових ґраток, кристалічних структур, правильних систем точок, пов’язаних елементами симетрії) • Подібно інверсійним і дзеркальним осям, гвинтові осі симетрії відповідають складній симетричній операції – повороту на певний елементарний кут (180, 120, 90, 60º) та одночасному переміщенню (поступанню t) у напрямку осі обертання

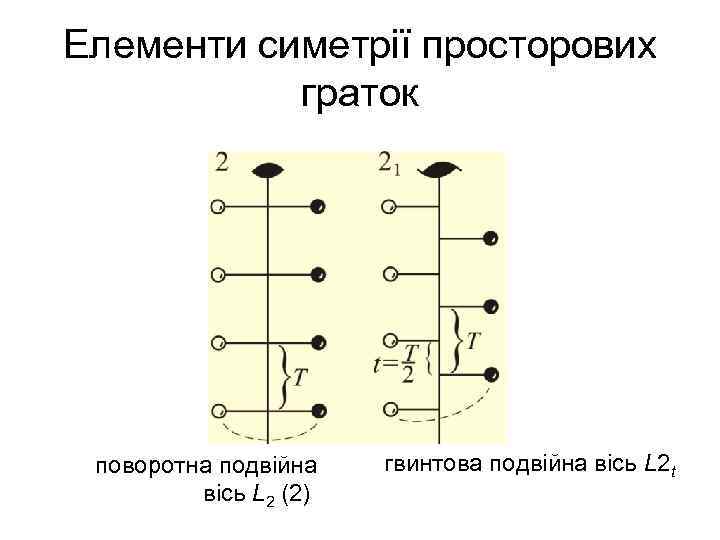Елементи симетрії просторових граток поворотна подвійна вісь L 2 (2) гвинтова подвійна вісь L 2 t

• В усіх гвинтових осях поступання t суміщене з дією звичайної поворотної осі L 3, L 4, L 6 • Величина поступання , де і – індекс, а n – порядок осі

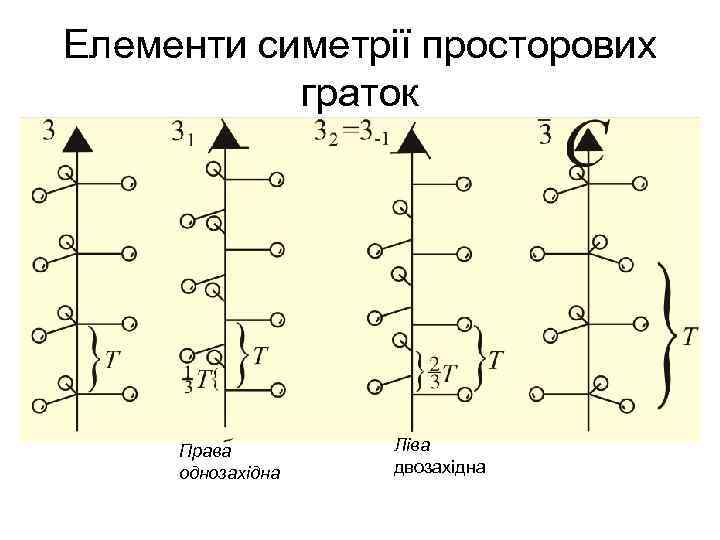Елементи симетрії просторових граток Права однозахідна Ліва двозахідна

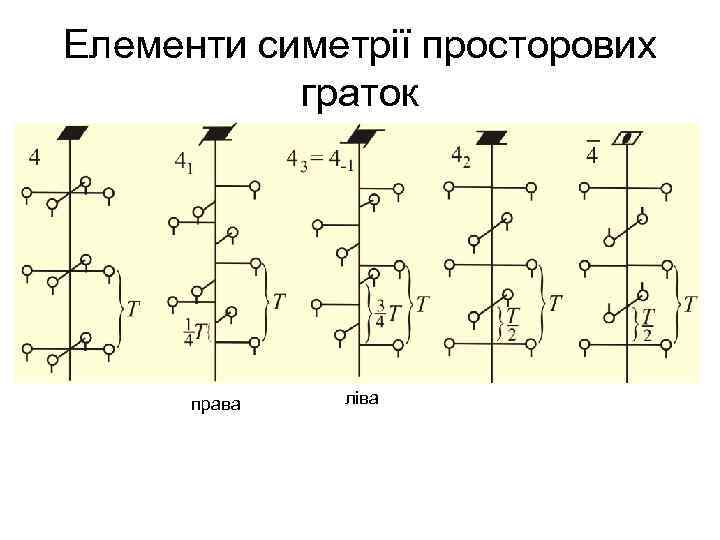Елементи симетрії просторових граток права ліва

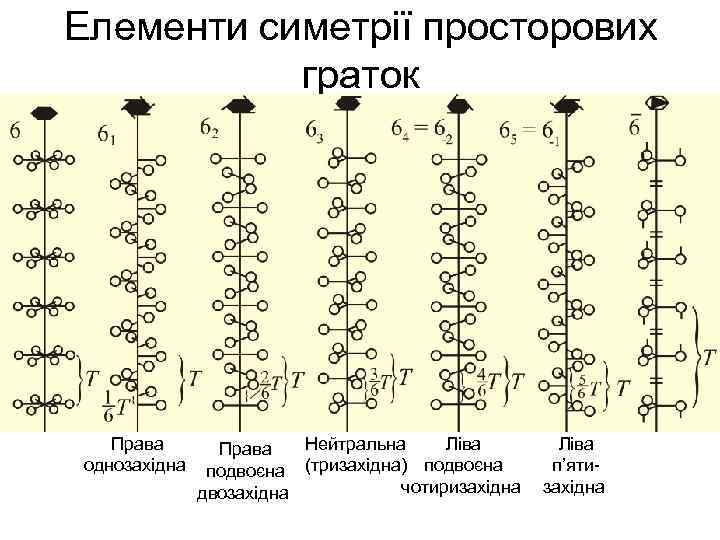Елементи симетрії просторових граток Права Нейтральна Ліва Права однозахідна подвоєна (тризахідна) подвоєна п’ятичотиризахідна двозахідна

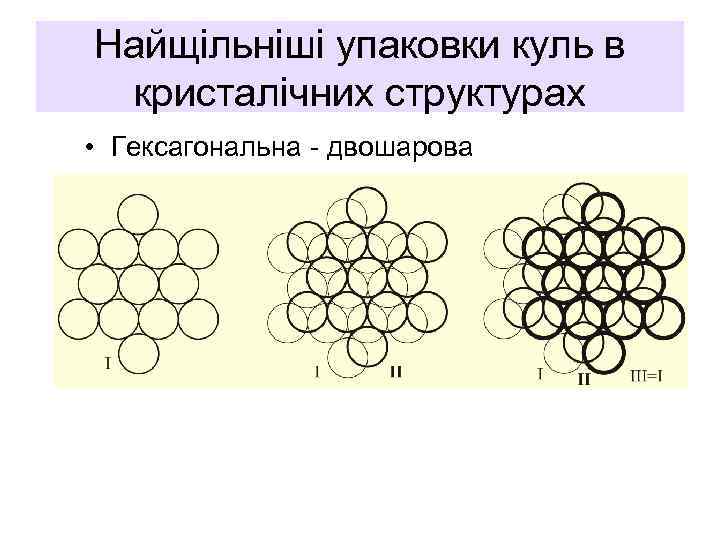Найщільніші упаковки куль в кристалічних структурах • Гексагональна - двошарова

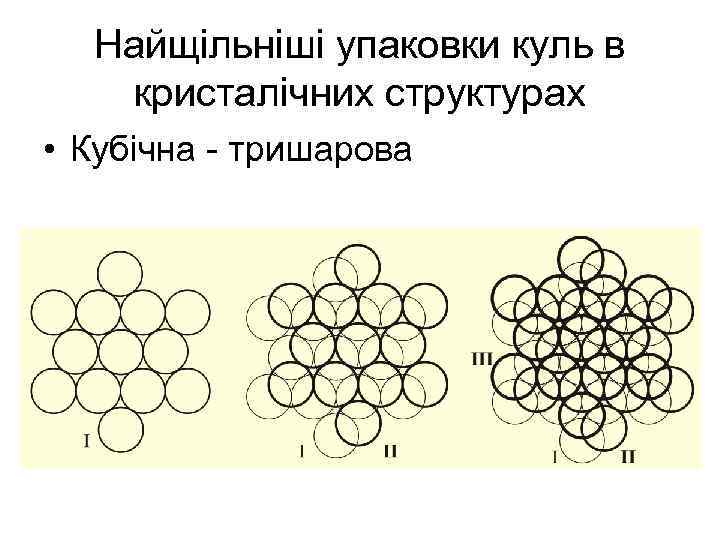Найщільніші упаковки куль в кристалічних структурах • Кубічна - тришарова

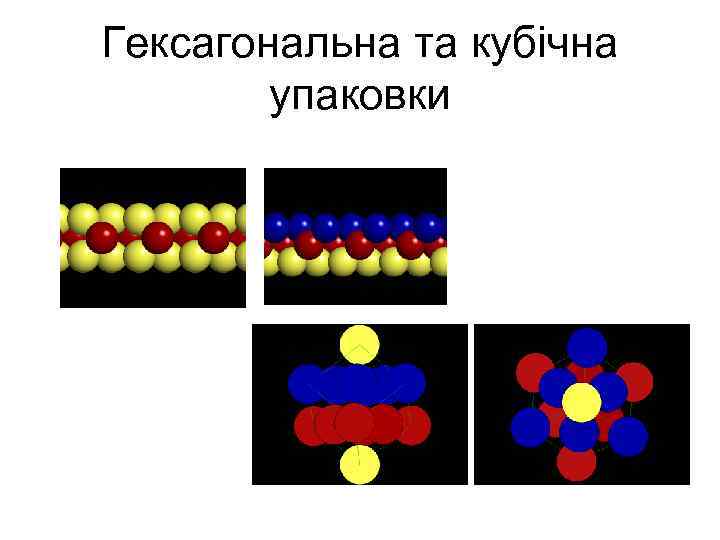Гексагональна та кубічна упаковки

Найщільніша упаковка • Реалізується у випадках – іонного та металічного зв’язку – Коли радіуси катіонів та аніонів близькі або ж катіон вільно входить в інтерстиційні пустоти упаковки аніонів • Структура більшості мінералів тільки наближається до найщільнішої упаковки

Порожнини в упаковці 26% щільно упакованої моноатомної структури - це порожнини – інтерстиції між атомами: Ø - тетраедричні – менші за розміром, обмежені Тетраедрична чотирма атомами порожнина Ø - октаедричні – більші за розміром, обмежені шістьома атомами на n куль припадає 2 n тетраедричних і n октаедричних пустот Октаедрична порожнина

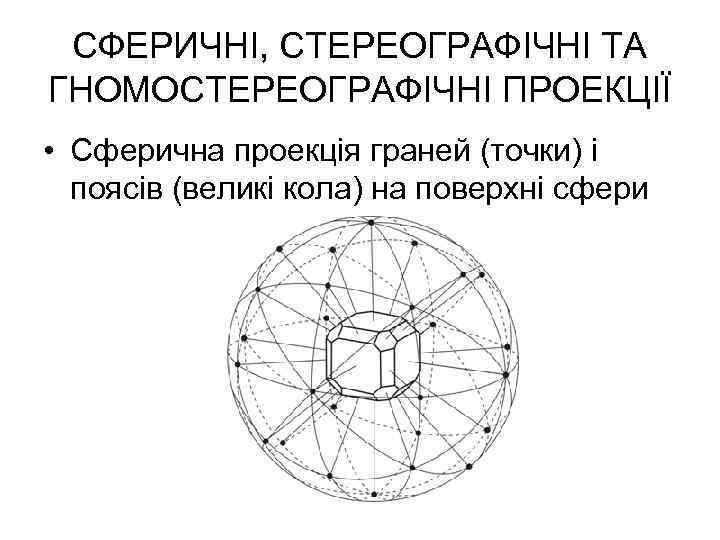СФЕРИЧНІ, СТЕРЕОГРАФІЧНІ ТА ГНОМОСТЕРЕОГРАФІЧНІ ПРОЕКЦІЇ • Сферична проекція граней (точки) і поясів (великі кола) на поверхні сфери

• Кожна з нормалей до граней кристала представлена на сфері відповідною точкою, яка називається полюсом грані • Всі грані, полюси котрих лежать на одному великому колі сферичної проекції належать до однієї зони (поясу) кристала • Кутові взаємовідносини між гранями кристала повністю зберігаються на сферичній проекції • Кути на сфері між полюсами граней відповідають кутам між перпендикулярами до граней. Вони є додатковими до внутрішніх кутів між гранями кристалу

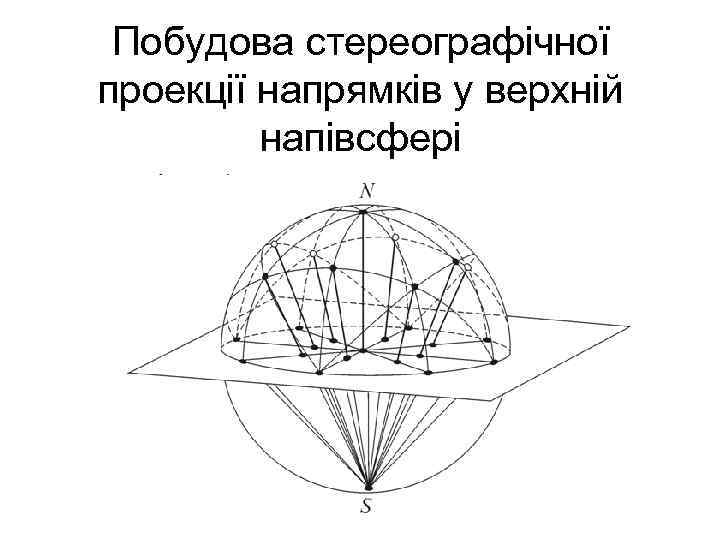Побудова стереографічної проекції напрямків у верхній напівсфері

• Стереографічною проекцією похилої площини, що проходить через центр сфери, буде дуга великого кола • Стереографічна проекція горизонтальної площини співпаде з екваторіальним колом проекції • По мірі зменшення кута нахилу площин кривизна відповідних дуг буде зменшуватись. У граничному випадку з вертикальною площиною одержимо пряму лінію, яка є діаметром екваторіального кола проекції

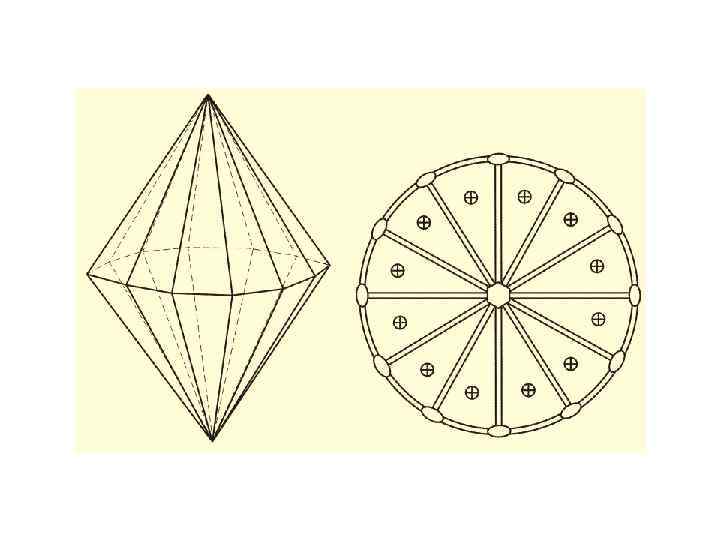
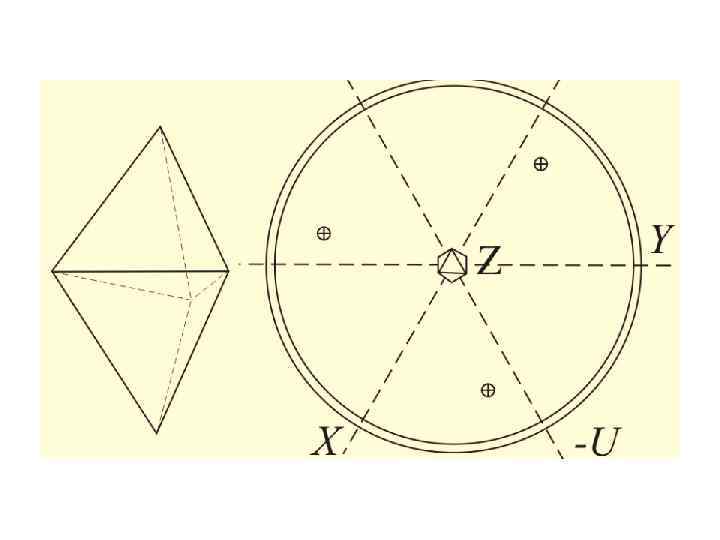
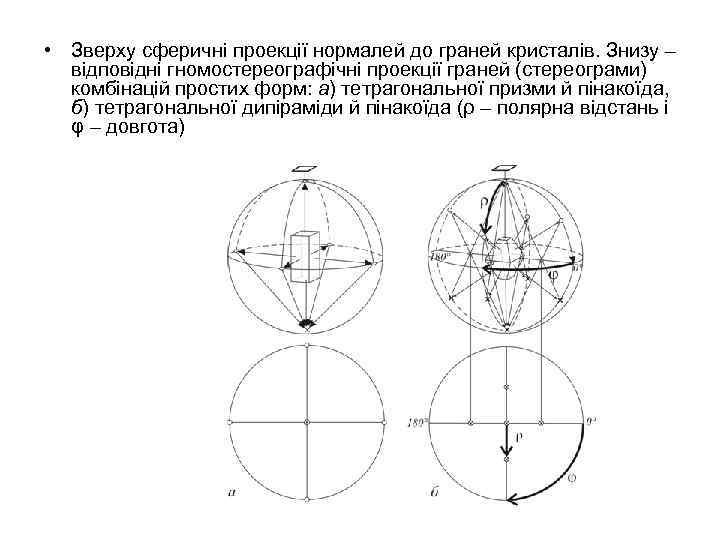• Зверху сферичні проекції нормалей до граней кристалів. Знизу – відповідні гномостереографічні проекції граней (стереограми) комбінацій простих форм: а) тетрагональної призми й пінакоїда, б) тетрагональної дипіраміди й пінакоїда (ρ – полярна відстань і φ – довгота)

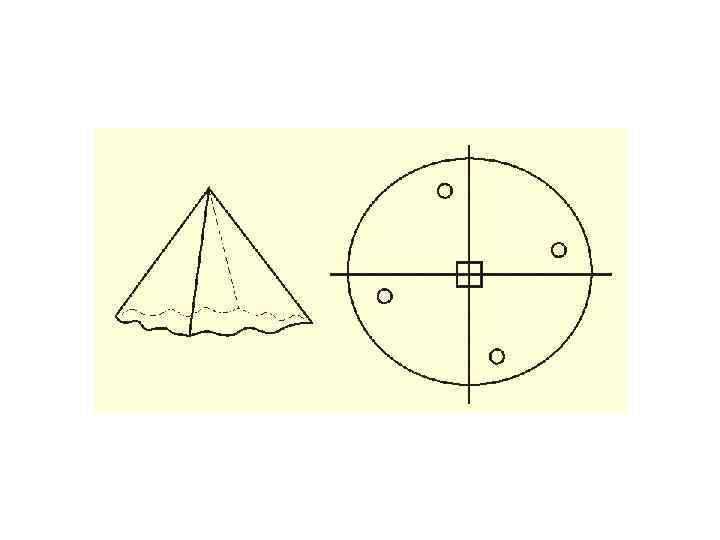
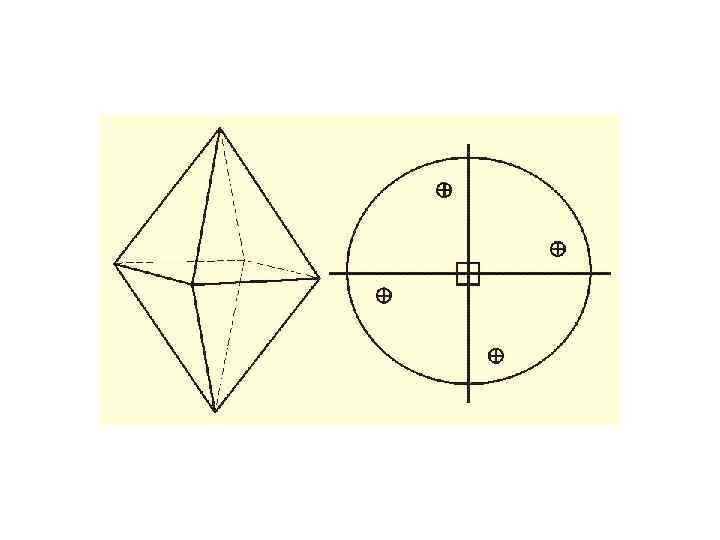
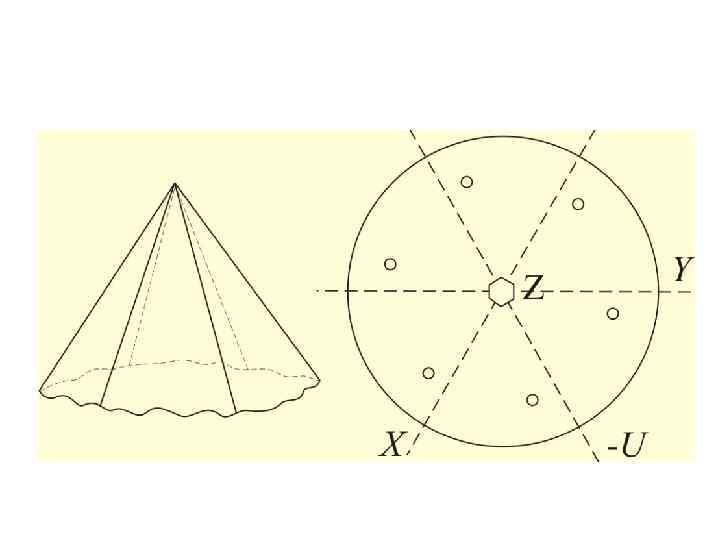
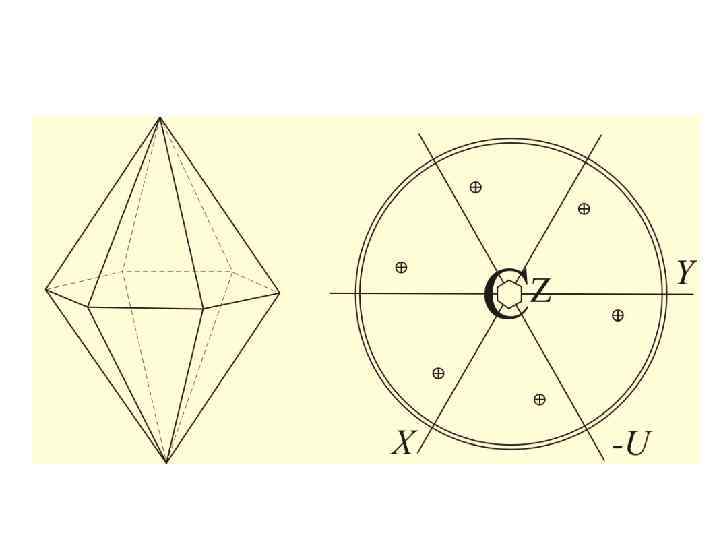
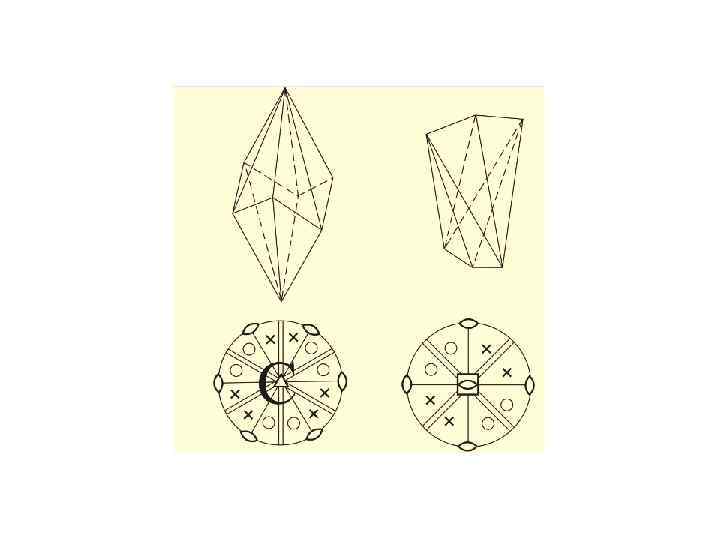
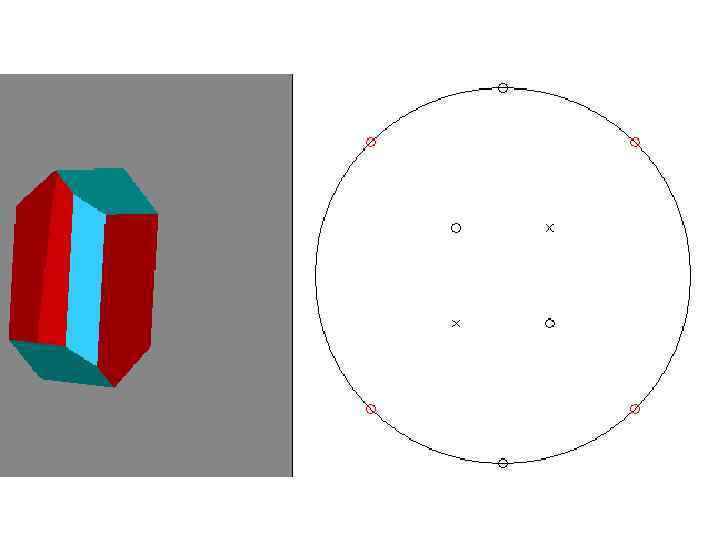
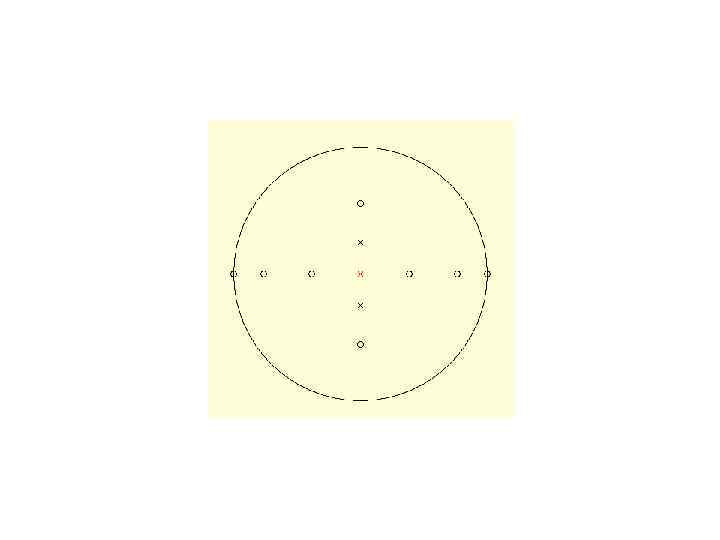
Проектування кристалів • спочатку будують стереографічну проекцію його елементів симетрії, а потім на неї наносять гномостереографічні проекції граней (полюси граней) • стереографічна проекція вектора, що виходить у верхній напівсфері, відмічена маленьким кружечком (○), а вектора у нижній напівсфері – хрестиком ( ) • горизонтальні грані (нормалі до них вертикальні!) проектують у центр кола проекцій • вертикальні грані (нормалі до них горизонтальні, ρ = 90°) – на коло • Проекції нахилених граней розміщують всередині кола. Чим грань ближча до вертикальної, тим точка (проекція грані) виявляється ближчою до екваторіального кола; і навпаки, чим грань більш полога, тим її проекція виявляється ближчою до центра кола. • полюси всіх вертикальних граней розміщуються на лінії екватора, їх позначають лише кружечками • коли проекції верхньої і нижньої граней на стереограмі потрапляють в одну точку, то кожну з них позначають відповідним значком: верхню – кружечком, нижню – хрестиком.