Kris Gaj Research and teaching interests cryptography

Kris Gaj Research and teaching interests: • cryptography • computer arithmetic • FPGA design and verification Contact: Engineering Bldg. , room 3225 kgaj@gmu. edu (703) 993 -1575 Office hours: Monday, 6: 00 -7: 00 PM, Tuesday 7: 30 -8: 30 PM, Thursday, 4: 30 -5: 30 PM, and by appointment

ECE 645 Part of: MS in Cp. E Digital Systems Design – pre-approved course Other concentration areas – elective course MS in EE Certificate in VLSI Design/Manufacturing Ph. D in ECE Ph. D in IT

DIGITAL SYSTEMS DESIGN 1. ECE 545 Digital System Design with VHDL – K. Gaj, project, FPGA design with VHDL, Xilinx & Altera FPGAs 2. ECE 645 Computer Arithmetic – K. Gaj, project, FPGA design with VHDL, Xilinx & Altera FPGAs 3. ECE 586 Digital Integrated Circuits – D. Ioannou, homework/small projects 4. ECE 681 VLSI Design for ASICs – TK Ramesh, project/lab, front-end and back-end ASIC design with Synopsys tools 5. ECE 682 VLSI Test Concepts – T. Storey, homework

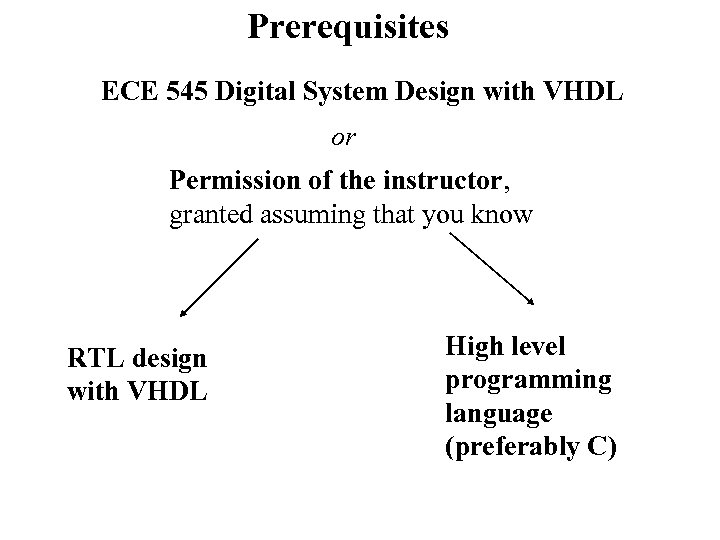Prerequisites ECE 545 Digital System Design with VHDL or Permission of the instructor, granted assuming that you know RTL design with VHDL High level programming language (preferably C)

Prerequisite knowledge • This class assumes proficiency with FPGA CAD tools from ECE 545 • You are expected to be proficient with: – Synthesizable VHDL coding – Advanced VHDL testbenches, including file input/output – FPGA synthesis and post-synthesis simulation – FPGA implementation and timing simulation – Reading and interpreting all synthesis and implementation reports

Course web page ECE web page Courses Course web pages ECE 645 http: //ece. gmu. edu/coursewebpages/ECE 645/S 12/

Computer Arithmetic Lecture Homework 10 % Midterm exam (in class) 15 % Final Exam (in class) 25 % Project 1 20 % Project 2 30 %

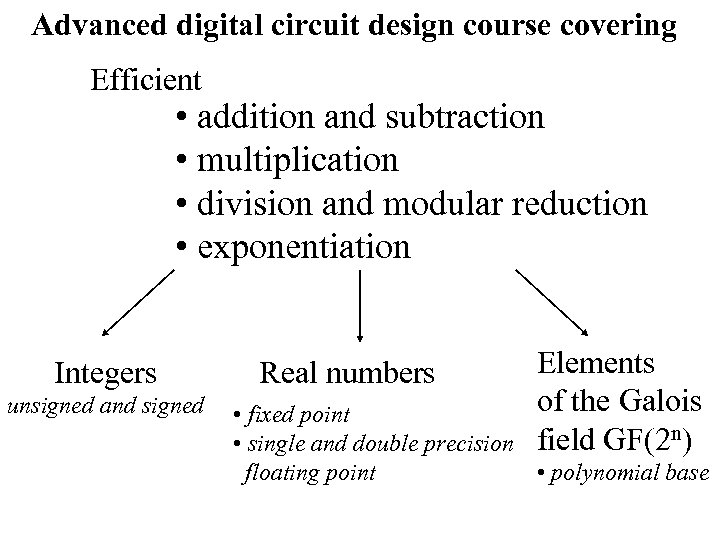Advanced digital circuit design course covering Efficient • addition and subtraction • multiplication • division and modular reduction • exponentiation Integers unsigned and signed Real numbers Elements of the Galois field GF(2 n) • fixed point • single and double precision floating point • polynomial base

Lecture topics INTRODUCTION 1. Applications of computer arithmetic algorithms.

ADDITION AND SUBTRACTION 1. Basic addition, subtraction, and counting 2. Addition in Xilinx and Altera FPGAs 3. Carry-lookahead, carry-select, and hybrid adders 4. Adders based on Parallel Prefix Networks 5. Pipelined Adders

MULTIOPERAND ADDITION 1. Sequential multi-operand adders 2. Carry Save Adders 3. Wallace and Dadda Trees

NUMBER REPRESENTATIONS • Unsigned Integers • Signed Integers • Fixed-point real numbers • Floating-point real numbers • Elements of the Galois Field GF(2 n)

LONG INTEGER ARITHMETIC 1. Modular Multiplication 2. Modular Exponentiation 3. Montgomery Multipliers and Exponentiation Units

MULTIPLICATION 1. Tree and array multipliers 2. Unsigned vs. signed multipliers 3. Optimizations for squaring 4. Sequential multipliers - radix-2 multiplier - multipliers based on carry-save adders - radix-4 & radix-8 multipliers - Booth multipliers - serial multipliers

TECHNOLOGY 1. Embedded resources of Xilinx and Altera FPGAs - block memories - multipliers - DSP units 2. Multiplication in Xilinx and Altera FPGAs - using distributed logic - using embedded multipliers - using DSP blocks 3. Pipelined multipliers

DIVISION 1. Basic restoring and non-restoring sequential dividers 2. SRT and high-radix dividers 3. Array dividers

FLOATING POINT AND GALOIS FIELD ARITHMETIC 1. Floating-point units 2. Galois Field GF(2 n) units

Literature (1) Required textbook: Behrooz Parhami, Computer Arithmetic: Algorithms and Hardware Design, 2 nd edition, Oxford University Press, 2010.

Literature (2) Recommended textbooks: Jean-Pierre Deschamps, Gery Jean Antoine Bioul, Gustavo D. Sutter, Synthesis of Arithmetic Circuits: FPGA, ASIC and Embedded Systems, Wiley-Interscience, 2006. Milos D. Ercegovac and Tomas Lang Digital Arithmetic, Morgan Kaufmann Publishers, 2004. Isreal Koren, Computer Arithmetic Algorithms, 2 nd edition, A. K. Peters, Natick, MA, 2002.

Literature (2) VHDL books: 1. Pong P. Chu, RTL Hardware Design Using VHDL: Coding for Efficiency, Portability, and Scalability, Wiley-IEEE Press, 2006. 2. Volnei A. Pedroni, Circuit Design and Simulation with VHDL, 2 nd edition, The MIT Press, 2010. 1. 3. Sundar Rajan, Essential VHDL: RTL Synthesis Done Right 2. S & G Publishing, 1998.

Literature (3) Supplementary books: 1. E. E. Swartzlander, Jr. , Computer Arithmetic, vols. I and II, IEEE Computer Society Press, 1990. 2. Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone, Handbook of Applied Cryptology, Chapter 14, Efficient Implementation, CRC Press, Inc. , 1998.

Literature (3) Proceedings of conferences ARITH - International Symposium on Computer Arithmetic ASIL - Asilomar Conference on Signals, Systems, and Computers ICCD - International Conference on Computer Design CHES - Workshop on Cryptographic Hardware and Embedded Systems Journals and periodicals IEEE Transactions on Computers, in particular special issues on computer arithmetic. IEEE Transactions on Circuits and Systems IEEE Transactions on Very Large Scale Integration IEE Proceedings: Computer and Digital Techniques Journal of Signal Processing Systems

Homework • reading assignments • analysis of computer arithmetic algorithms and implementations • design of small hardware units using VHDL

Midterm exams Midterm Exam - 2 hrs 30 minutes, in class multiple choice + short problems Final Exam – 2 hrs 45 minutes comprehensive conceptual questions analysis and design of arithmetic units Practice exams on the web Tentative days of exams: Midterm Exam - Monday, March 26 Final Exam - Monday, May 14, 7: 30 -10: 15 PM

Project 1 Project I (individual, 20% of grade) Adders in Xilinx and Altera FPGAs Choosing optimal architecture for • combinational adder • pipelined adder in • Xilinx FPGAs (Virtex 5 & Virtex 6) • Altera FPGAs (Stratix III & Stratix IV) • ASICs (bonus) Done individually Final report & deliverables due Monday, March 19

Project 2 Project II (in groups of two or individually, 30% of grade) Modular Exponentiation of Large Integers or Floating Point Operations Investigation of alternative architectures for the best performance in terms of • Latency x Area product in • Xilinx FPGAs (Virtex 5 & Virtex 6) • Altera FPGAs (Stratix III & Stratix IV) • ASICs (bonus) Final report & deliverables due Monday, May 7

Primary applications (1) Execution units of general purpose microprocessors Integer units Floating point units Integers (8, 16, 32, 64 bits) Real numbers (32, 64 bits)

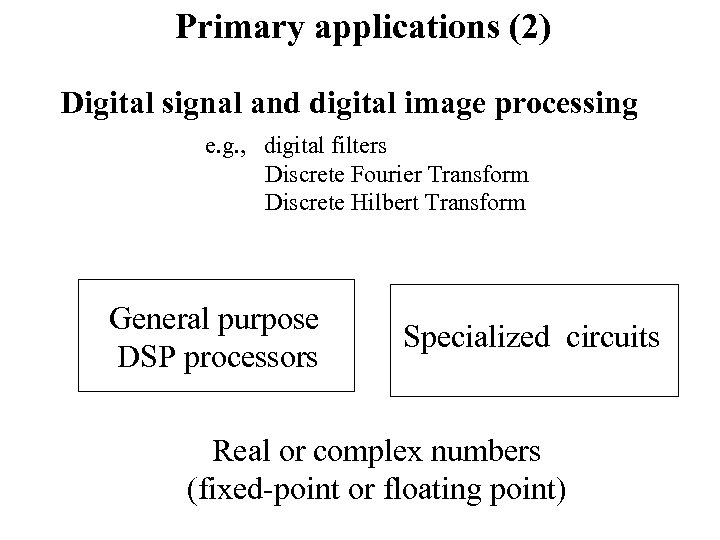Primary applications (2) Digital signal and digital image processing e. g. , digital filters Discrete Fourier Transform Discrete Hilbert Transform General purpose DSP processors Specialized circuits Real or complex numbers (fixed-point or floating point)

Primary applications (3) Coding Error detection codes Error correcting codes Elements of the Galois fields GF(2 n) (4 -64 bits)

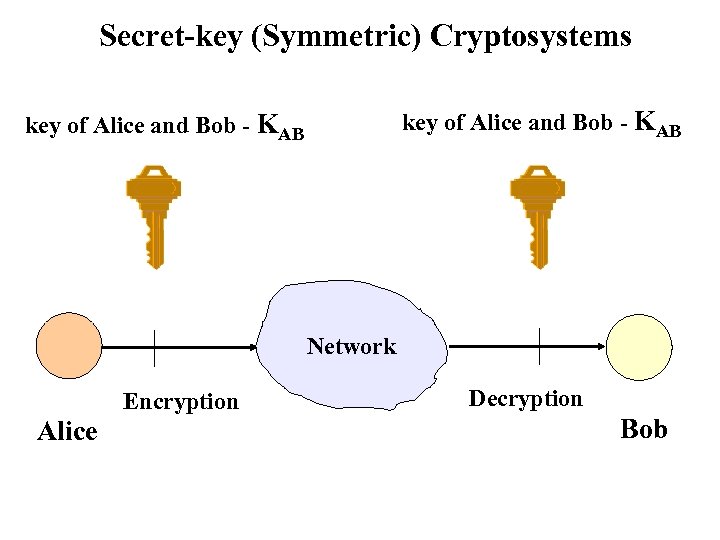Secret-key (Symmetric) Cryptosystems key of Alice and Bob - KAB Network Encryption Alice Decryption Bob

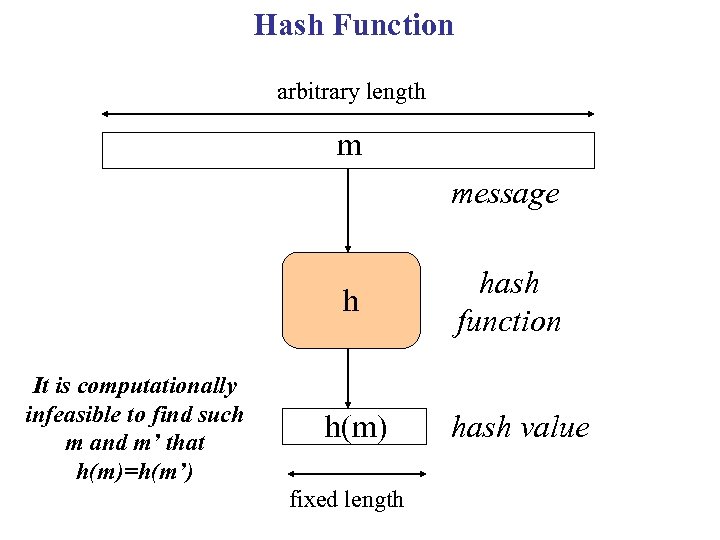Hash Function arbitrary length m message h It is computationally infeasible to find such m and m’ that h(m)=h(m’) h(m) fixed length hash function hash value

Primary applications (4) Cryptography IDEA, RC 6, Mars, SHA-3 candidates: SIMD, Shabal, Skein, BLAKE Integers (16, 32, 64 bits) Twofish, Rijndael, SHA-3 candidates Elements of the Galois field GF(2 n) (4, 8 bits)

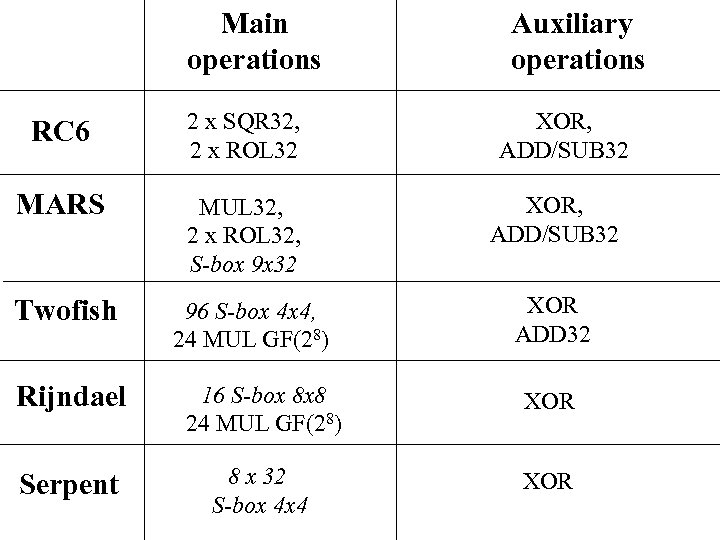Main operations RC 6 2 x SQR 32, 2 x ROL 32 MARS MUL 32, 2 x ROL 32, S-box 9 x 32 Twofish 96 S-box 4 x 4, 24 MUL GF(28) Auxiliary operations XOR, ADD/SUB 32 XOR ADD 32 Rijndael 16 S-box 8 x 8 24 MUL GF(28) XOR Serpent 8 x 32 S-box 4 x 4 XOR

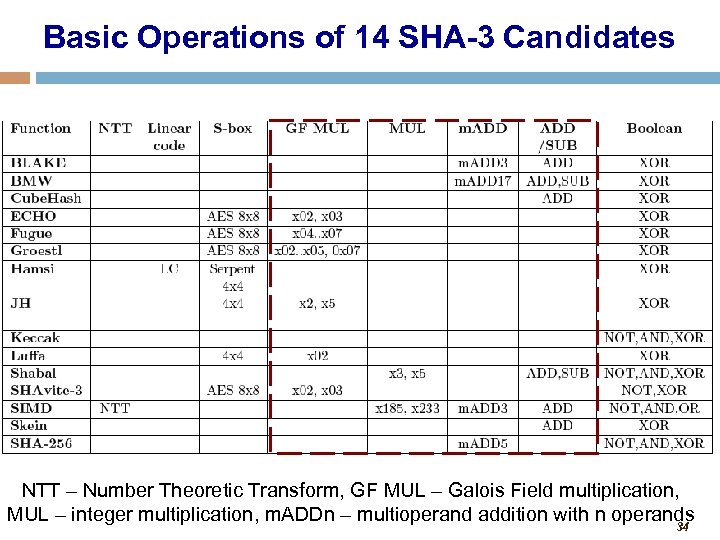Basic Operations of 14 SHA-3 Candidates NTT – Number Theoretic Transform, GF MUL – Galois Field multiplication, MUL – integer multiplication, m. ADDn – multioperand addition with 34 operands n 34

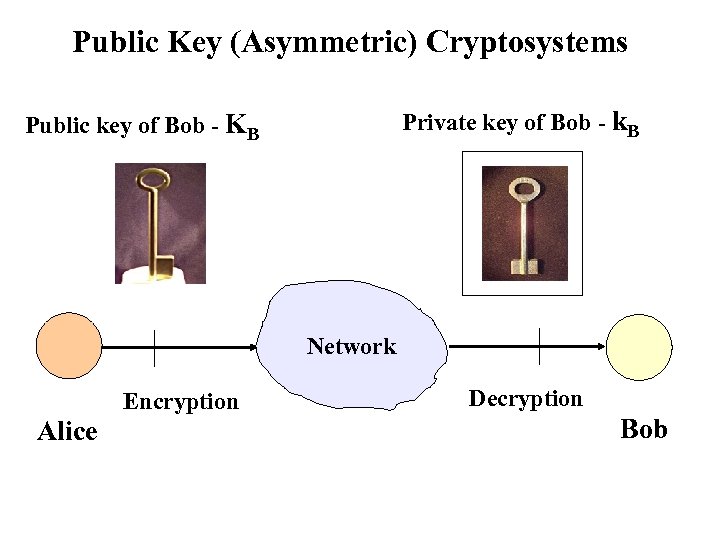Public Key (Asymmetric) Cryptosystems Private key of Bob - k. B Public key of Bob - KB Network Encryption Alice Decryption Bob

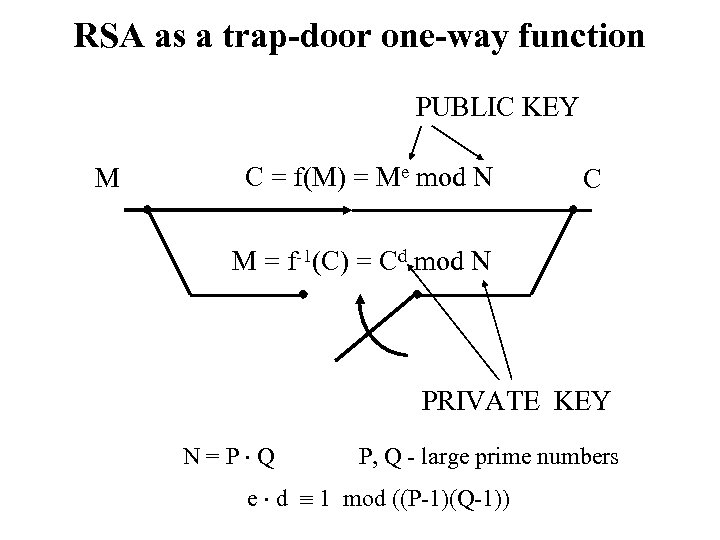RSA as a trap-door one-way function PUBLIC KEY M C = f(M) = Me mod N C M = f-1(C) = Cd mod N PRIVATE KEY N=P Q P, Q - large prime numbers e d 1 mod ((P-1)(Q-1))

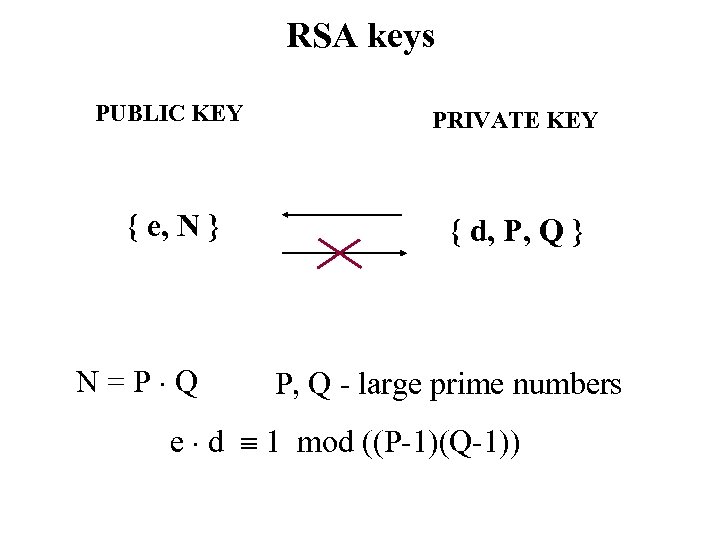RSA keys PUBLIC KEY PRIVATE KEY { e, N } { d, P, Q } N=P Q P, Q - large prime numbers e d 1 mod ((P-1)(Q-1))

Primary applications (5) Cryptography Public key cryptography RSA, Diffie-Hellman Long integers (1 k-16 k bits) Elliptic Curve Cryptosystems, Pairing Based Cryptosystems Elements of the Galois field GF(2 n) (160 -512 bits)

Primary applications (5) Cipher Breaking Public key cryptography RSA PUBLIC KEY RSA PRIVATE KEY { e, N } { d, P, Q } N=P Q P, Q e d 1 mod ((P-1)(Q-1))