КРИПТОГРАФИЧЕСКАЯ СТОЙКОСТЬ ойкий фр ст й ши

КРИПТОГРАФИЧЕСКАЯ СТОЙКОСТЬ

ойкий фр ст й ши Како Тот, который для успешной атаки требует от противника: • недостижимых вычислительных ресурсов • недостижимого объема перехваченных открытых или шифротекстов • такого времени раскрытия, что по его истечению информация станет неактуальной

Три типа стойкости шифров Вычислительная (практическая) стойкость Информационно-теоретическая (абсолютная) стойкость Доказуемая стойкость

Вычислительная стойкость шифра Для наилучшего алгоритма вскрытия шифра !!! Оценка базируется на теории сложности. Оценивается, исходя из двух позиций: § какова вычислительная сложность полного перебора ключей; § какие уязвимости имеет шифр

Вычислительная стойкость шифра Если алгоритм вскрытия шифра на современных мощных компьютерах должен выполнить ~280 операций, то шифр считается вычислительно защищенным ШИФР СДВИГА ШИФР ЗАМЕНЫ ШИФР ВИЖЕНЕРА DES AES RSA ШИФР ЭЛЬ-ГАМАЛЯ ЕСС

Теоретико-информационная (абсолютная) стойкость шифра криптоаналитик не может раскрыть криптосистему ни теоретически, ни практически, даже имея бесконечно большие вычислительные ресурсы Базируется на теории информации и теории вероятностей

Доказуемая стойкость шифра Доказательство стойкости криптосистемы сводят к решению определенной трудно решаемой математической проблемы, положенной в основу алгоритма

Клод Шеннон (Claude Shannon) – автор фундаментальных трудов по теории информации, электротехнике и криптографии 1916 – 2001 Ultimate Machine

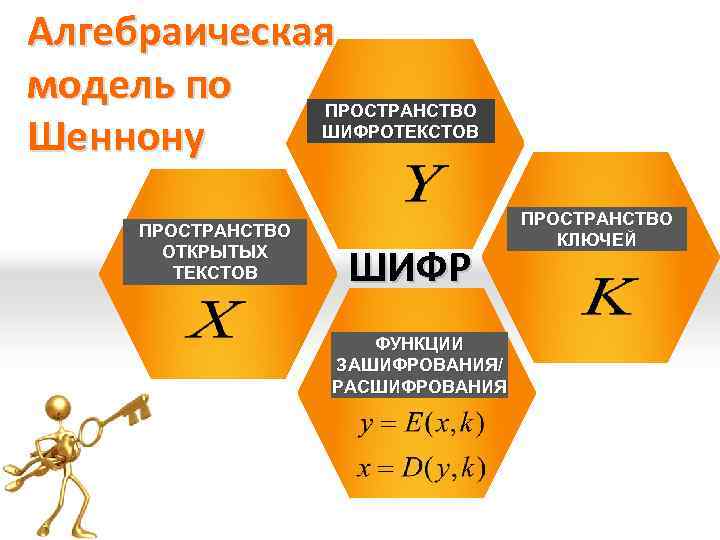Алгебраическая модель по ПРОСТРАНСТВО ШИФРОТЕКСТОВ Шеннону ПРОСТРАНСТВО ОТКРЫТЫХ ТЕКСТОВ ШИФР ФУНКЦИИ ЗАШИФРОВАНИЯ/ РАСШИФРОВАНИЯ ПРОСТРАНСТВО КЛЮЧЕЙ

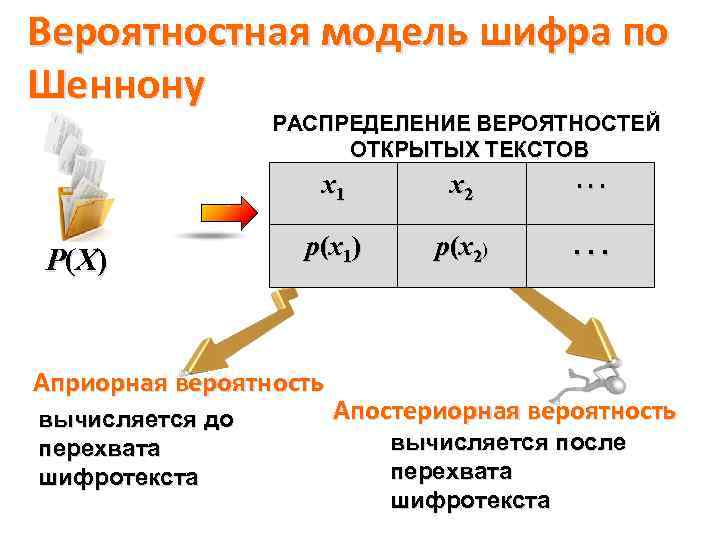Вероятностная модель шифра по Шеннону РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ОТКРЫТЫХ ТЕКСТОВ х1 Р (Х ) х2 . . . р(х1) р(х2) . . . Априорная вероятность вычисляется до перехвата шифротекста Апостериорная вероятность вычисляется после перехвата шифротекста

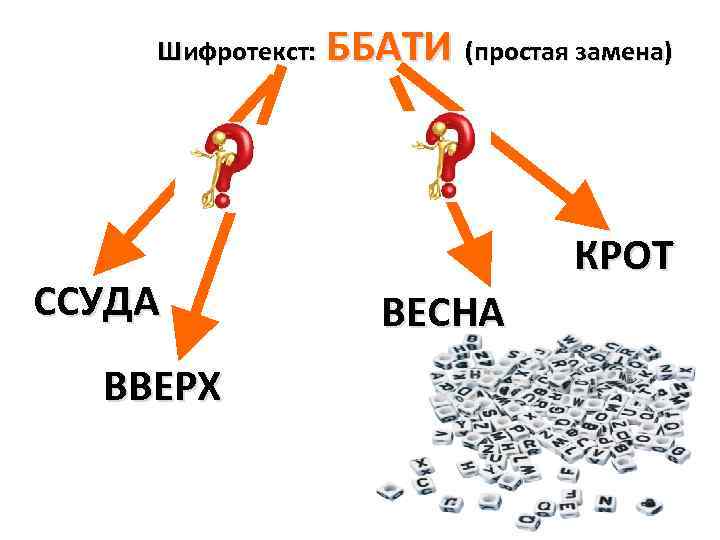Шифротекст: ССУДА ВВЕРХ ББАТИ (простая замена) КРОТ ВЕСНА

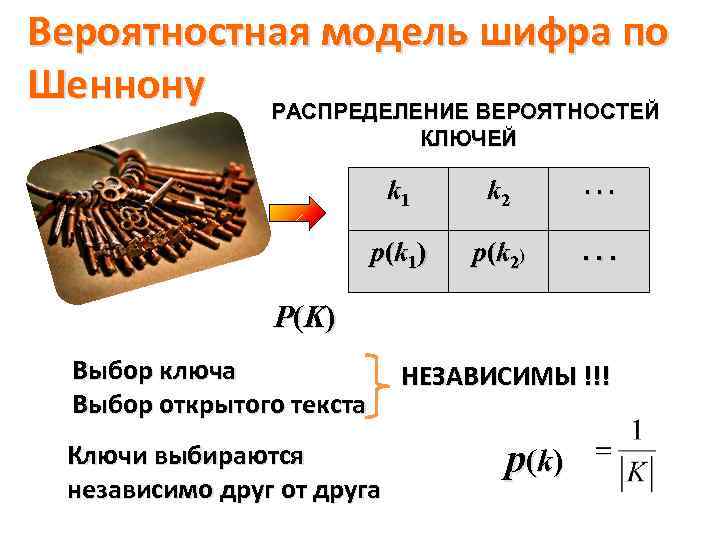Вероятностная модель шифра по Шеннону РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ КЛЮЧЕЙ k 1 k 2 . . . р(k 1) р(k 2) . . . Р (K ) Выбор ключа Выбор открытого текста Ключи выбираются независимо друг от друга НЕЗАВИСИМЫ !!! p(k)

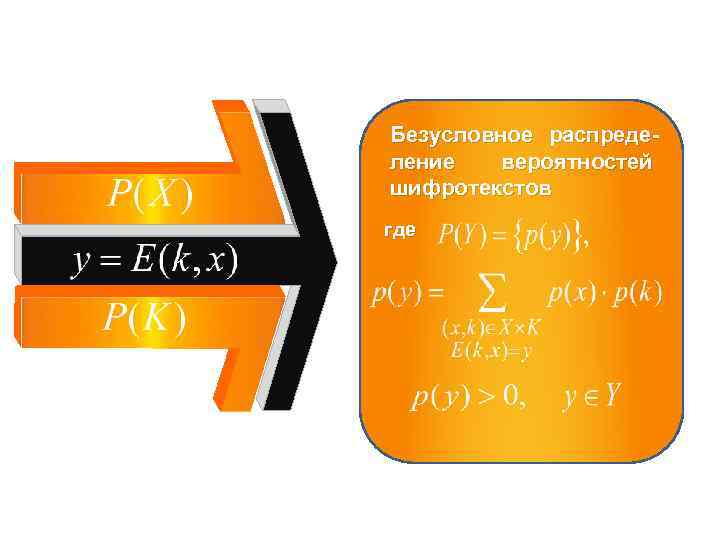Безусловное распределение вероятностей шифротекстов где

Вероятностная модель по Шеннону ШИФР РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ОТКРЫТЫХ ТЕКСТОВ Р (Х ) РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ КЛЮЧЕЙ Р (K )

Что может найти криптоаналитик Условную вероятность появления шифротекста у, если выбрано сообщение х Условную вероятность появления шифротекста у, если выбран ключ k

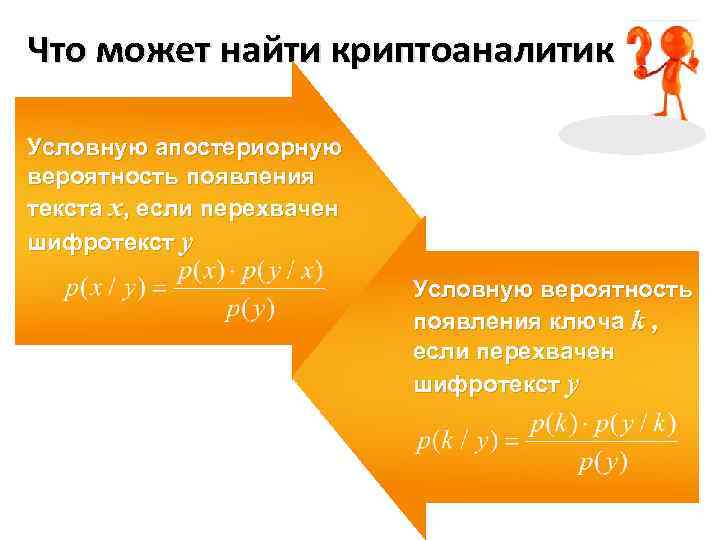Что может найти криптоаналитик Условную апостериорную вероятность появления текста х, если перехвачен шифротекст у Условную вероятность появления ключа k , если перехвачен шифротекст у

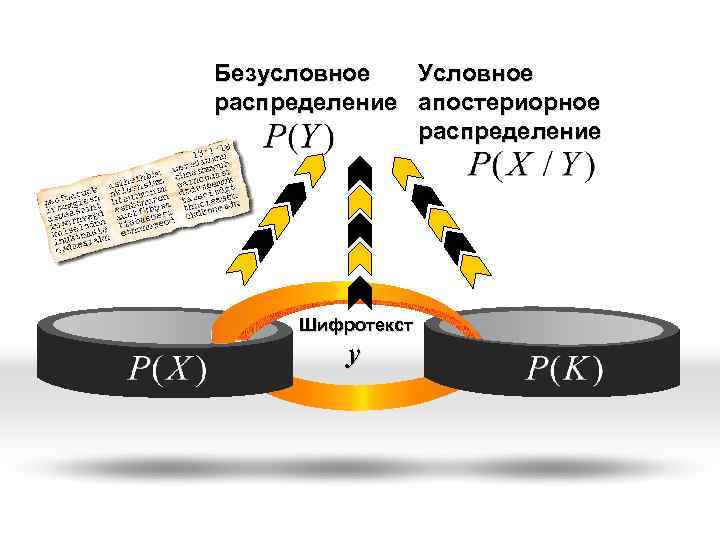Безусловное Условное распределение апостериорное распределение Шифротекст у

ПРИМЕР. Распределение вероятностей открытых текстов текст вероятность Распределение вероятностей ключ вероятность пространство шифротекстов

Функция зашифрования задана таблицей Найдем распределение вероятностей шифротекстов:

Условные вероятности шифротекста у при условии, что выбран открытый текст x;

Условные апостериорные вероятности открытого текста x при условии, что перехвачен шифротекст y.

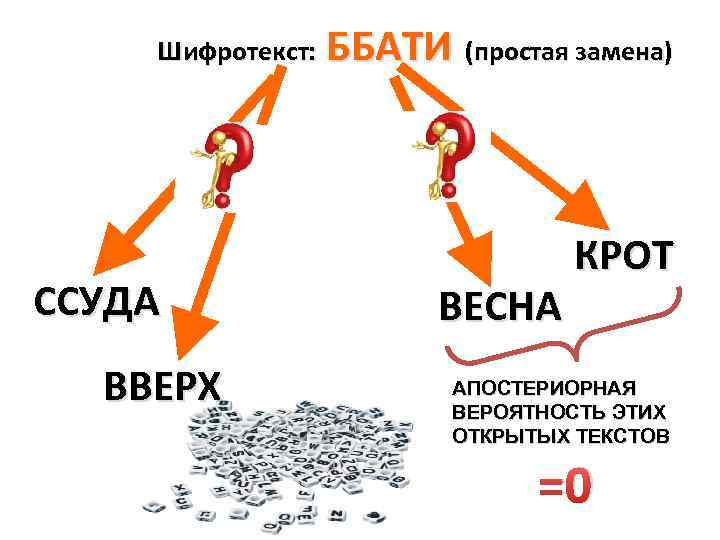Шифротекст: ССУДА ВВЕРХ ББАТИ (простая замена) ВЕСНА КРОТ АПОСТЕРИОРНАЯ ВЕРОЯТНОСТЬ ЭТИХ ОТКРЫТЫХ ТЕКСТОВ =0

КАКОЙ ШИФР ЯВЛЯЕТСЯ СОВЕРШЕННО СТОЙКИМ ? ? КАК ФОРМАЛИЗОВАТЬ ОТВЕТ

Шифр – совершенно (абсолютно) стойкий, если шифротекст не содержит какой-либо информации о ключе и шифруемом открытом тексте, кроме, возможно, его длины

Для совершенно стойкого шифра дешифрование по вероятности успеха эквивалентно простому угадыванию открытого текста в отсутствие каких-либо дополнительных данных КАК ФОРМАЛИЗОВАТЬ ЭТИ ОПРЕДЕЛЕНИЯ?

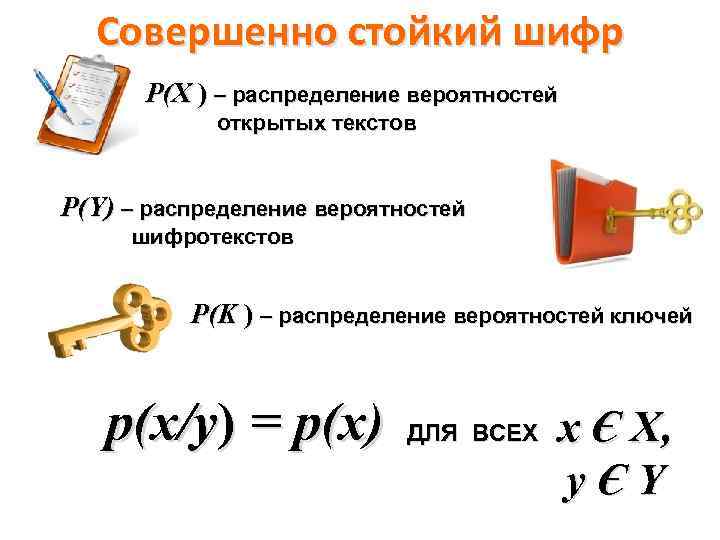Совершенно стойкий шифр Р(Х ) – распределение вероятностей открытых текстов Р(Y) – распределение вероятностей шифротекстов Р(K ) – распределение вероятностей ключей p(x/y) = p(x) ДЛЯ ВСЕХ x Є Х, уЄY

Совершенно стойкий шифр По формуле Байеса Условие совершенной стойкости шифра эквивалентно p(y/x ) = p(у) ДЛЯ ВСЕХ x Є Х, уЄY

Теорема : для совершенно стойкого шифра Доказательство: – верно для всех шифров. Для совершенно стойкого шифра для ключ при котором найдется иначе противоречит условию

Шифр называется идеально стойким, если невозможно однозначно восстановить открытый текст по известному шифротексту сколь угодной длины. Будет ли совершенно стойкий шифр идеально стойким ДА!

НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СОВЕРШЕННОЙ СТОЙКОСТИ ШИФРА Теорема: чтобы шифр, у которого был совершенно стойким, необходимо и достаточно, чтобы: Для любых х Є Х и y Є Y существовал только один ключ k Є K, при котором y=E(x, k) 2. Распределение Р(K) вероятностей ключей было равномерным (р(k) =1/|K|)

Для совершенно стойкого шифра ключ находится по паре из уравнения Дли на к не м люч ень а до тек ста ше дл лжн ины а бы ть отк рыт ого