Краткий курс начертательной геометрии для студентов машиностроительных специальностей

Краткий курс начертательной геометрии для студентов машиностроительных специальностей Автор Морозов С. А.

ВВЕДЕНИЕ Предметом начертательной геометрии, как и геометрии вообще, являются пространственные формы и отношения между ними. Начертательную геометрию из геометрии в целом выделяет особенность ее метода , основанного на операции проецирования и операции сечения. Аппаратом и средством решения задач в начертательной геометрии являются чертежи, выполненные на уровне полных графических моделей соответствующих пространственных форм и отношений. Начертательная геометрия является теоретической основой построения технических чертежей, которые представляют собой полные графические модели конкретных инженерных изделий. n Изучение начертательной геометрии способствует развитию пространственного представления и воображения, конструктивно геометрического мышления, развитию способностей к анализу и синтезу пространственных форм и отношений между ними. Освоению способов конструирования различных геометрических пространственных объектов (в основном - поверхностей), способов получения их чертежей на уровне графических моделей и умению решать на этих чертежах задачи, связанные с пространственными объектами и их геометрическими характеристиками. Основание начертательной геометрии как науке было положено французским ученым и инженером Гаспаром Монжем (1746 -1818) в его труде “Начертательная геометрия”, Париж, 1795 г. n Гаспар Монж дал общий метод решения стереометрических задач геометрическими построениями на плоскости, то есть на чертеже, с помощью чертежных инструментов. Отсюда следует: n Методом начертательной геометрии является графический метод, основанный, как было сказано выше, на операции проецирования. Поэтому большинство чертежей, рассматриваемых в курсе начертательной геометрии, называются проекционными чертежами. n

Принятые обозначения n n n n Точки - заглавными буквами латинского алфавита: А, В, С, D, . . . ; Линии - строчными буквами латинского алфавита, : a, b, с, d, . . . ; Поверхности - строчными буквами греческого алфавита с дополнительными индексами “градусов”: °, . . . ; Плоскости проекций: 1 - горизонтальная, 2 - фронтальная, 3 профильная или любая другая дополнительная плоскость; 4, 5, . . . - дополнительные плоскости проекций. Оси проекций - строчными буквами латинского алфавита: х, y и z. Начало координат - цифрой 0. Последовательность точек, линий или поверхностей подстрочными индексами: А 1, В 1, С 1, . . . , а 1, b 1, . . . . Проекции на плоскостях: 1 – АI, ВI, CI, . . . , a. I, b. I, . . . , I, . . . ; 2 – АII, ВII, CII, . . . , a. II, b. II, . . . , II, . . . ; 3 – АIII, ВIII, CIII, . . . , a. III, b. III, . . . , III, . . . ; 4 - АIV, ВIV, CIV, . . . , a. IV, b. IV, . . . , IV, . …;

n n n Горизонтальные линии - буквой h; горизонтальный след плоскости - h 0 ; Фронтальные линии - буквой f; фронтальный след плоскости f 0 ; Профильные линии - буквой р; профильный след плоскости р0 ; Точки схода следов плоскости - х0, y 0, z 0; В случае преобразовании эпюра (комплексного чертежа) вращением или плоскопараллельным перемещением: Обозначение точек, прямых, плоскостей, углов: после первого преобразования А 1 I, A 1 II, …a 1 I, a 1 II, …α 1 I, α 1 II, β 1 II; после второго преобразования А 2 I, A 2 II, …a 2 I, a 2 II, …α 2 I, α 2 II, β 2 II; Вспомогательные точки - цифрами 1, 2, 3, . .

Символическая запись операций: n n n n n Точка А лежит на прямой m - А m ; Прямая n проходит через точку А - n A; = - совпадают, равны, результат действия; - параллельны - а b ; - перпендикулярно - а b; - пересечение множеств - m = K; - конъюнкция предложений - соответствует союзу “и”; - импликация - логическое следствие, означает “если. . . то”. - эквивалентность.

Тема 1 Комплексный чертеж. 1. ПОНЯТИЕ ОБ ОПЕРАЦИИ ПРОЕЦИРОВАНИЯ n Аппарат проецирования состоит из двух основных частей и таких аппаратов проецирования в основном два: аппарат центрального проецирования и аппарат параллельного проецирования. n Аппарат центрального проецирования состоит из плоскости проекций и центра проецирования S. Причем центр проецирования не принадлежит плоскости проекций (рис. 1. 1). Проецирование осуществляется с помощью проецирующих лучей, исходящих из центра проецирования S. n Аппарат параллельного проецирования состоит из плоскости проекций и направления проецирования S, которое не параллельно плоскости проекций (рис. 1. 2). Проецирующие лучи, в данном случае, проводятся параллельно направлению S. n В точке пересечения проецирующего луча с плоскостью проекций и располагается соответствующая проекция точки. Проекции точек, как и сами точки, обозначаются заглавными буквами латинского алфавита, но с соответствующими индексами. На рис. 1. 1 и 1. 2 они обозначены индексами “штрих”. n Частным случаем параллельного проецирования является проецирование ортогональное, то есть прямоугольное, когда направление проецирования S перпендикулярно плоскости проекций. Этот способ является основным способом проецирования, принятым при построении технических чертежей. Рис. 1. 1 Рис. 1. 2

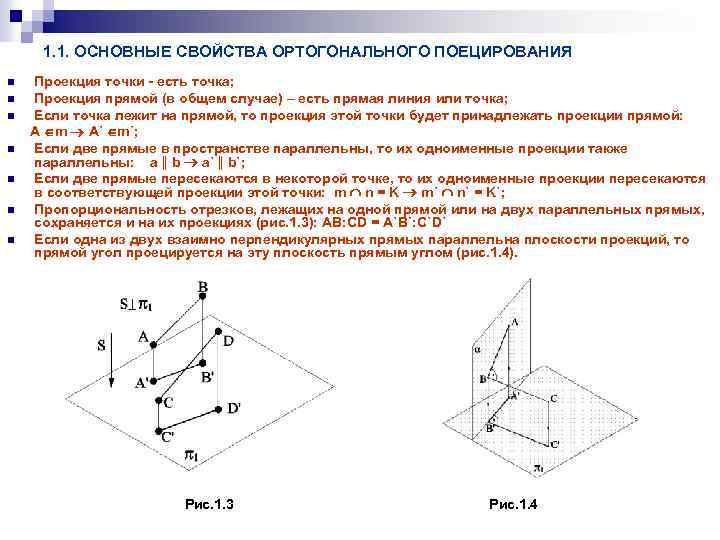1. 1. ОСНОВНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПОЕЦИРОВАНИЯ n n n n Проекция точки - есть точка; Проекция прямой (в общем случае) – есть прямая линия или точка; Если точка лежит на прямой, то проекция этой точки будет принадлежать проекции прямой: А m A` m`; Если две прямые в пространстве параллельны, то их одноименные проекции также параллельны: a b a` b`; Если две прямые пересекаются в некоторой точке, то их одноименные проекции пересекаются в соответствующей проекции этой точки: m n = K m` n` = K`; Пропорциональность отрезков, лежащих на одной прямой или на двух параллельных прямых, сохраняется и на их проекциях (рис. 1. 3): АВ: СD = А`B`: C`D` Если одна из двух взаимно перпендикулярных прямых параллельна плоскости проекций, то прямой угол проецируется на эту плоскость прямым углом (рис. 1. 4). Рис. 1. 3 Рис. 1. 4

1. 2. ЭПЮР ГАСПАРА МОНЖА ИЛИ КОМПЛЕКСНЫЙ ЧЕРТЕЖ n n Чертежи в начертательной геометрии строятся главным образом на основании операции ортогонального, то есть прямоугольного, проецирования на две взаимно перпендикулярные плоскости проекций: фронтальную и горизонтальную плоскости. Полученные таким образом два изображения позволяют однозначно определять положение того или иного геометрического образа (фигуры) в пространстве. (рис. 1. 5). Путем вращения одной из этих плоскостей проекций вокруг линии пересечения - оси х, до совмещения в единую плоскость получается плоское изображение, которое называют эпюром Гаспара Монжа или комплексным чертежом. Покажем это на примере изображения точки А (рис. 1. 5 и 1. 6). Плоскости 1 и 2 делят пространство на четыре четверти, отмеченные римскими цифрами. Рис. 1. 5 Рис. 1. 6

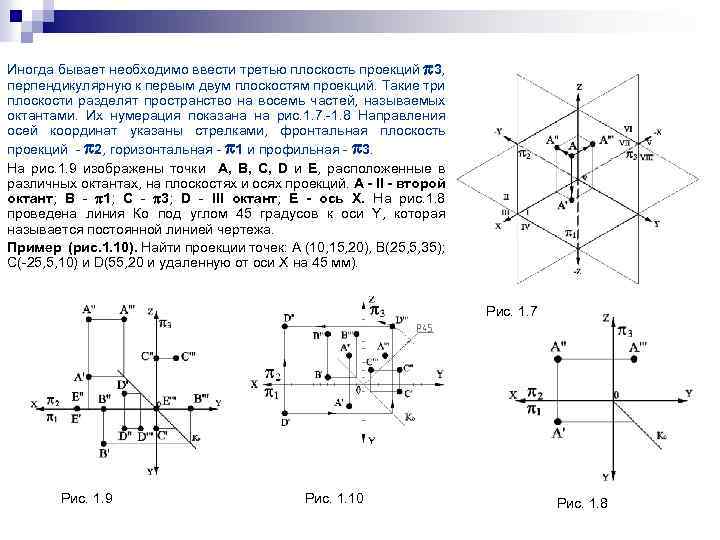Иногда бывает необходимо ввести третью плоскость проекций 3, перпендикулярную к первым двум плоскостям проекций. Такие три плоскости разделят пространство на восемь частей, называемых октантами. Их нумерация показана на рис. 1. 7. -1. 8 Направления осей координат указаны стрелками, фронтальная плоскость проекций - 2, горизонтальная - 1 и профильная - 3. На рис. 1. 9 изображены точки А, В, С, D и Е, расположенные в различных октантах, на плоскостях и осях проекций. А - II - второй октант; В - 1; С - 3; D - III октант; Е - ось Х. На рис. 1. 8 проведена линия Ко под углом 45 градусов к оси Y, которая называется постоянной линией чертежа. Пример (рис. 1. 10). Найти проекции точек: А (10, 15, 20), В(25, 5, 35); С(-25, 5, 10) и D(55, 20 и удаленную от оси X на 45 мм). Рис. 1. 7 Рис. 1. 9 Рис. 1. 10 Рис. 1. 8

БЕЗОСНЫЙ КОМПЛЕКСНЫЙ ЧЕРТЕЖ Постоянная линия комплексного чертежа - линия Ко- позволяет обойтись без применения осей проекций. Такие чертежи широко применяются в проекционном черчении (рис. 1. 11). Рис. 1. 11 При необходимости оси проекций всегда могут быть построены, выбраны в любом месте, с началом координат на линии Ко.

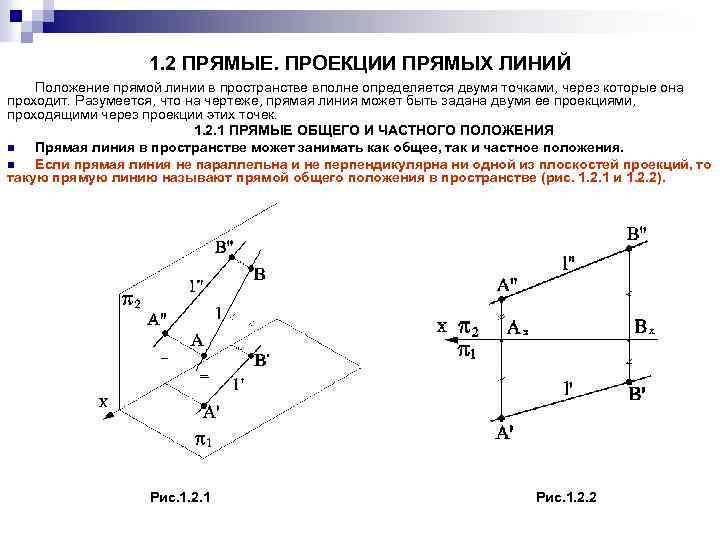1. 2 ПРЯМЫЕ. ПРОЕКЦИИ ПРЯМЫХ ЛИНИЙ Положение прямой линии в пространстве вполне определяется двумя точками, через которые она проходит. Разумеется, что на чертеже, прямая линия может быть задана двумя ее проекциями, проходящими через проекции этих точек. 1. 2. 1 ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ n Прямая линия в пространстве может занимать как общее, так и частное положения. n Если прямая линия не параллельна и не перпендикулярна ни одной из плоскостей проекций, то такую прямую линию называют прямой общего положения в пространстве (рис. 1. 2. 1 и 1. 2. 2). Рис. 1. 2. 1 Рис. 1. 2. 2

К прямым линиям частного положения, относятся прямые линии, параллельные одной из плоскостей проекций и прямые, перпендикулярные к одной из плоскостей проекций. Прямые линии перпендикулярные к одной из плоскостей проекций будут в то же время параллельными двум другим плоскостям проекций. n Прямые линии, параллельные одной из плоскостей проекций, называются прямыми уровня. n Среди них различают: n прямую параллельную горизонтальной плоскости проекций (Горизонтальная прямая уровня Горизонталь), которую обозначают буквой h (рис. 1. 2. 3); n прямую параллельную фронтальной плоскости проекций (Фронтальная прямая уровня Фронталь), которую обозначают буквой f (рис. 1. 2. 4); n Прямую, параллельную профильной плоскости проекций (Профильная прямая уровня), которую обозначают буквой р. (рис. 1. 2. 5). n Рис. 1. 2. 3 Рис. 1. 2. 4 Рис. 1. 2. 5

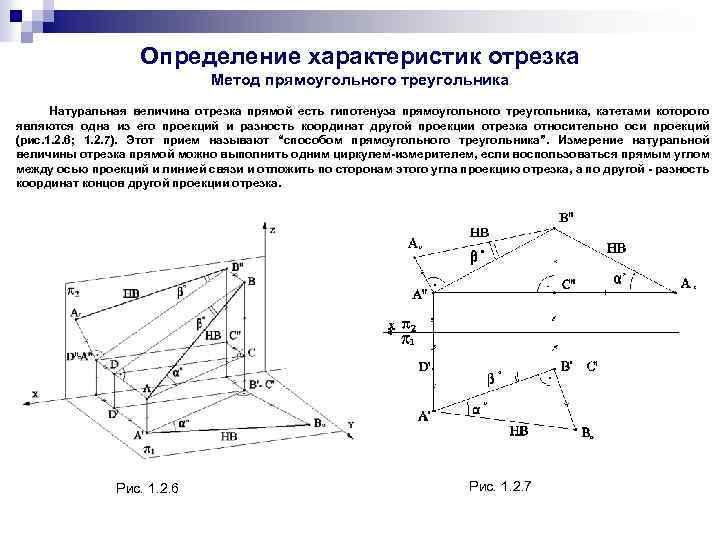Определение характеристик отрезка Метод прямоугольного треугольника Натуральная величина отрезка прямой есть гипотенуза прямоугольного треугольника, катетами которого являются одна из его проекций и разность координат другой проекции отрезка относительно оси проекций (рис. 1. 2. 6; 1. 2. 7). Этот прием называют “способом прямоугольного треугольника”. Измерение натуральной величины отрезка прямой можно выполнить одним циркулем-измерителем, если воспользоваться прямым углом между осью проекций и линией связи и отложить по сторонам этого угла проекцию отрезка, а по другой - разность координат концов другой проекции отрезка. Рис. 1. 2. 6 Рис. 1. 2. 7

Среди прямых, перпендикулярных к плоскостям проекций, выделяют : n горизонтально проецирующие прямые - прямые, перпендикулярные к горизонтальной плоскости проекций (рис. 1. 2. 8); n фронтально проецирующие прямые – прямые, перпендикулярные к фронтальной плоскости проекций (рис. 1. 2. 9); n профильно проецирующие прямые – прямые, перпендикулярные к профильной плоскости проекций (рис. 1. 2. 10). Рис. 1. 2. 8 Рис. 1. 2. 9 Рис. 1. 2. 10

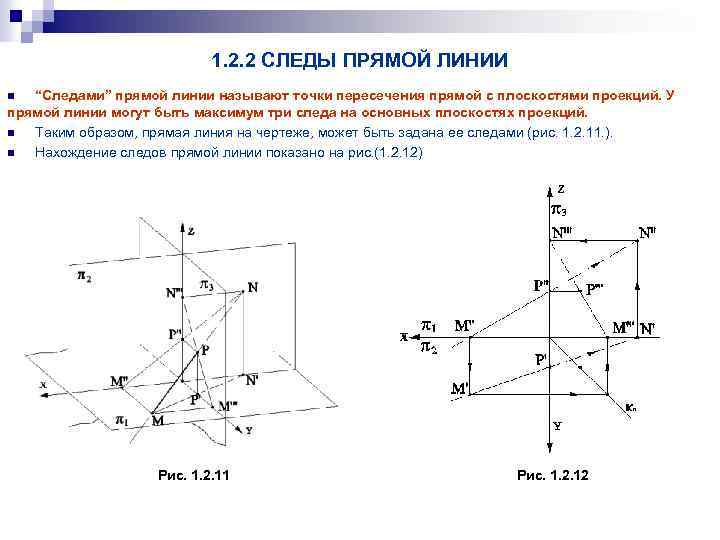1. 2. 2 СЛЕДЫ ПРЯМОЙ ЛИНИИ “Следами” прямой линии называют точки пересечения прямой с плоскостями проекций. У прямой линии могут быть максимум три следа на основных плоскостях проекций. n Таким образом, прямая линия на чертеже, может быть задана ее следами (рис. 1. 2. 11. ). n Нахождение следов прямой линии показано на рис. (1. 2. 12) n Рис. 1. 2. 11 Рис. 1. 2. 12

1. 2. 3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ В ПРОСТРАНСТВЕ n n Из стереометрии известно, что две прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися. (рис. 1. 2. 13, 1. 2. 14, 1. 2. 15). Рис. 1. 2. 13 Рис. 1. 2. 14 Рис. 1. 2. 15 Видимость двух скрещивающихся прямых (одна прямая на той или иной плоскости проекций может перекрывать другую прямую или быть перекрыта этой прямой). Для определения “видимости” линий в этом случае можно воспользоваться так называемыми “конкурирующими” точками, то есть точками, лежащими на одной проецирующей прямой. На рис. 2. 15 такими конкурирующими точками являются точки 1 и 2 и 3 и 4.

Контрольные вопросы 1. Какие проекции наиболее наглядны? а) центральные б) параллельные 2. Где расположен центр проекций при параллельном проецировании? а) на плоскости проекций б) в бесконечности 3. Сколько плоскостей проекций нужно использовать для обратимости чертежа? а) одну б) две в) три 4. Какой способ проецирования используется в методе Монжа? а) центральный б) ортогональный в) косоугольный 5. Какое минимальное количество проекций точки достаточно задать на комплексном чертеже? а) одну б) две в) три

6. Какие координаты определяют горизонтальную проекцию точки? а) х и у б) у и z в) х и z 7. Какие координаты определяют фронтальную проекцию точки? а) х и у б) у и z в) х и z Какие координаты определяют профильную проекцию точки? а) х и у б) у и z в) х и z Сколько одинаковых координат имеют конкурирующие точки? а) все б) одну в) две

ТЕСТЫ