Lektsia_5_lozh_kor.ppt
- Количество слайдов: 40
 Корреляция и причинность Две переменные х и у могут иметь сильную корреляцию, но прежде чем делать выводы необходимо подумать и проинтерпретировать эту взаимосвязь. Взаимосвязь переменных может быть вызвана другим фактором (третьей переменной), влияющим на х и у. Если Вы видите пожарную машину на каждом из пожаров, то это не означает, что пожарные машины вызывают пожар.
Корреляция и причинность Две переменные х и у могут иметь сильную корреляцию, но прежде чем делать выводы необходимо подумать и проинтерпретировать эту взаимосвязь. Взаимосвязь переменных может быть вызвана другим фактором (третьей переменной), влияющим на х и у. Если Вы видите пожарную машину на каждом из пожаров, то это не означает, что пожарные машины вызывают пожар.
 Ложная корреляция Для выявления ложных корреляций рассматривают не пару, а множество «потенциально важных» значений, и используют частные корреляции. Если зафиксировать пожары примерно одного масштаба, и посчитать корреляцию между количеством пожарных и ущербом, то корреляция окажется обратной.
Ложная корреляция Для выявления ложных корреляций рассматривают не пару, а множество «потенциально важных» значений, и используют частные корреляции. Если зафиксировать пожары примерно одного масштаба, и посчитать корреляцию между количеством пожарных и ущербом, то корреляция окажется обратной.
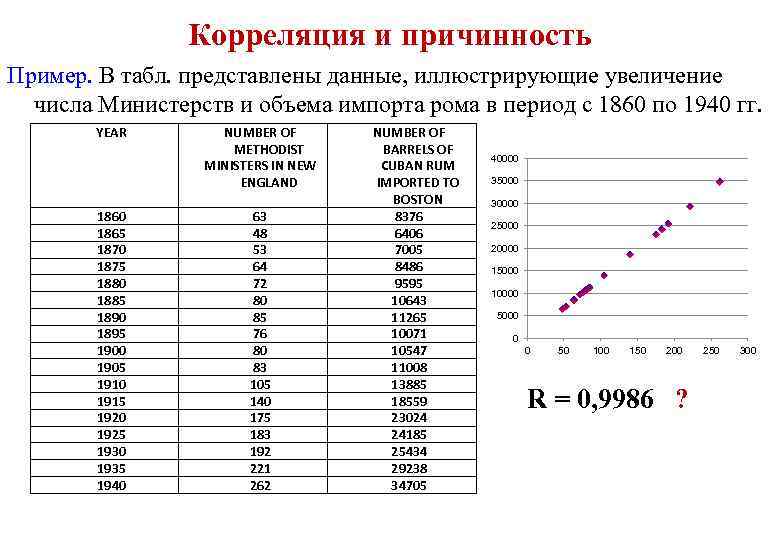 Корреляция и причинность Пример. В табл. представлены данные, иллюстрирующие увеличение числа Министерств и объема импорта рома в период с 1860 по 1940 гг. YEAR 1860 1865 1870 1875 1880 1885 1890 1895 1900 1905 1910 1915 1920 1925 1930 1935 1940 NUMBER OF METHODIST MINISTERS IN NEW ENGLAND 63 48 53 64 72 80 85 76 80 83 105 140 175 183 192 221 262 NUMBER OF BARRELS OF CUBAN RUM IMPORTED TO BOSTON 8376 6406 7005 8486 9595 10643 11265 10071 10547 11008 13885 18559 23024 24185 25434 29238 34705 40000 35000 30000 25000 20000 15000 10000 5000 0 0 50 100 150 200 R = 0, 9986 ? 250 300
Корреляция и причинность Пример. В табл. представлены данные, иллюстрирующие увеличение числа Министерств и объема импорта рома в период с 1860 по 1940 гг. YEAR 1860 1865 1870 1875 1880 1885 1890 1895 1900 1905 1910 1915 1920 1925 1930 1935 1940 NUMBER OF METHODIST MINISTERS IN NEW ENGLAND 63 48 53 64 72 80 85 76 80 83 105 140 175 183 192 221 262 NUMBER OF BARRELS OF CUBAN RUM IMPORTED TO BOSTON 8376 6406 7005 8486 9595 10643 11265 10071 10547 11008 13885 18559 23024 24185 25434 29238 34705 40000 35000 30000 25000 20000 15000 10000 5000 0 0 50 100 150 200 R = 0, 9986 ? 250 300
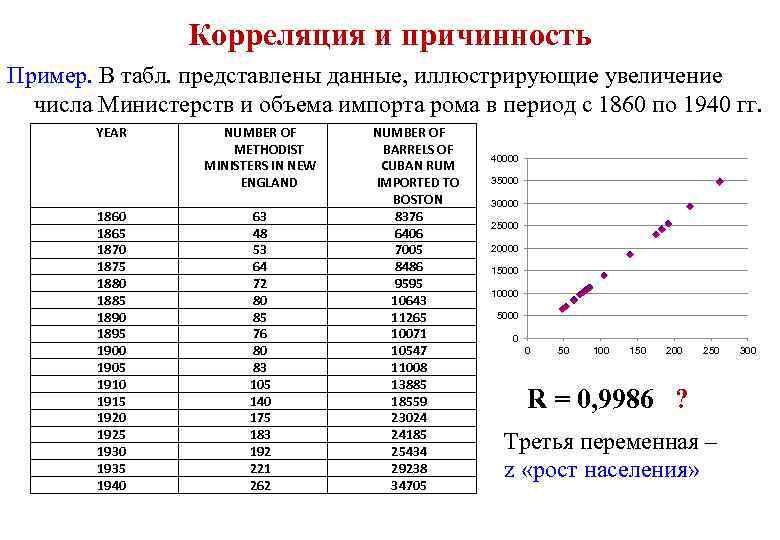 Корреляция и причинность Пример. В табл. представлены данные, иллюстрирующие увеличение числа Министерств и объема импорта рома в период с 1860 по 1940 гг. YEAR 1860 1865 1870 1875 1880 1885 1890 1895 1900 1905 1910 1915 1920 1925 1930 1935 1940 NUMBER OF METHODIST MINISTERS IN NEW ENGLAND 63 48 53 64 72 80 85 76 80 83 105 140 175 183 192 221 262 NUMBER OF BARRELS OF CUBAN RUM IMPORTED TO BOSTON 8376 6406 7005 8486 9595 10643 11265 10071 10547 11008 13885 18559 23024 24185 25434 29238 34705 40000 35000 30000 25000 20000 15000 10000 5000 0 0 50 100 150 200 250 R = 0, 9986 ? Третья переменная – z «рост населения» 300
Корреляция и причинность Пример. В табл. представлены данные, иллюстрирующие увеличение числа Министерств и объема импорта рома в период с 1860 по 1940 гг. YEAR 1860 1865 1870 1875 1880 1885 1890 1895 1900 1905 1910 1915 1920 1925 1930 1935 1940 NUMBER OF METHODIST MINISTERS IN NEW ENGLAND 63 48 53 64 72 80 85 76 80 83 105 140 175 183 192 221 262 NUMBER OF BARRELS OF CUBAN RUM IMPORTED TO BOSTON 8376 6406 7005 8486 9595 10643 11265 10071 10547 11008 13885 18559 23024 24185 25434 29238 34705 40000 35000 30000 25000 20000 15000 10000 5000 0 0 50 100 150 200 250 R = 0, 9986 ? Третья переменная – z «рост населения» 300
 Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных ! Если удалось установить тесную зависимость между двумя исследуемыми переменными, отсюда еще не следует их причинная взаимообусловленность.
Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных ! Если удалось установить тесную зависимость между двумя исследуемыми переменными, отсюда еще не следует их причинная взаимообусловленность.
 Трудности в интерпретации ПКК, связанные с опосредованным влиянием других переменных Пример (из кн. Айвазян С. А. , Енюков И. С. , Мешалкин Л. Д. Прикладная статистика: Исследование зависимостей. 1985) При анализе большого числа наблюдений, относящихся к отливке труб, была установлена положительная корреляционная связь между (x 1) временем плавки и (x 2) количеством забракованных труб Дать причинное истолкование такой стохастической зависимости невозможно (рекомендация ограничить продолжительность плавки для снижения брака малосостоятельна). Причина?
Трудности в интерпретации ПКК, связанные с опосредованным влиянием других переменных Пример (из кн. Айвазян С. А. , Енюков И. С. , Мешалкин Л. Д. Прикладная статистика: Исследование зависимостей. 1985) При анализе большого числа наблюдений, относящихся к отливке труб, была установлена положительная корреляционная связь между (x 1) временем плавки и (x 2) количеством забракованных труб Дать причинное истолкование такой стохастической зависимости невозможно (рекомендация ограничить продолжительность плавки для снижения брака малосостоятельна). Причина?
 Трудности в интерпретации ПКК, связанные с опосредованным влиянием других переменных Пример Спустя несколько лет обнаружили, что большая продолжительность плавки связана с использованием сырья специального состава. Этот вид сырья приводил одновременно к длительному времени плавки и большому проценту брака, хотя оба этих фактора независимы. Таким образом, высокий коэффициент корреляции x 1 и x 2 обуславливался влиянием третьего, не учтенного фактора – характеристики качества сырья.
Трудности в интерпретации ПКК, связанные с опосредованным влиянием других переменных Пример Спустя несколько лет обнаружили, что большая продолжительность плавки связана с использованием сырья специального состава. Этот вид сырья приводил одновременно к длительному времени плавки и большому проценту брака, хотя оба этих фактора независимы. Таким образом, высокий коэффициент корреляции x 1 и x 2 обуславливался влиянием третьего, не учтенного фактора – характеристики качества сырья.
 Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Если бы этот фактор был учтен, то никакой значимой корреляционной связи между x 1 и x 2 не было бы обнаружено. За счет подобных эффектов (одновременного влияния неучтенных факторов на исследуемые переменные) может искажаться истинный смысл связи межу переменными. Такую корреляционную связь называют ложной! необходимо исследовать …. .
Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Если бы этот фактор был учтен, то никакой значимой корреляционной связи между x 1 и x 2 не было бы обнаружено. За счет подобных эффектов (одновременного влияния неучтенных факторов на исследуемые переменные) может искажаться истинный смысл связи межу переменными. Такую корреляционную связь называют ложной! необходимо исследовать …. .
 Пример 1 Искажающее влияние «третьего фактора» на корреляцию между двумя изучаемыми переменными По итогам года были получены следующие показатели работы 37 однородных предприятий легкой промышленности: x 0 (y) - среднемесячная характеристика качества ткани (в баллах), x 1 – среднемесячное количество профилактических наладок линии, x 2 – среднемесячное число обрывов линии. Проверка статистической значимости показала отсутствие статистически значимой парной корреляционной связи между x 0 и x 1, что не согласуется с профессиональными представлениями технолога.
Пример 1 Искажающее влияние «третьего фактора» на корреляцию между двумя изучаемыми переменными По итогам года были получены следующие показатели работы 37 однородных предприятий легкой промышленности: x 0 (y) - среднемесячная характеристика качества ткани (в баллах), x 1 – среднемесячное количество профилактических наладок линии, x 2 – среднемесячное число обрывов линии. Проверка статистической значимости показала отсутствие статистически значимой парной корреляционной связи между x 0 и x 1, что не согласуется с профессиональными представлениями технолога.
 Пример 1 Искажающее влияние «третьего фактора» на корреляцию между двумя изучаемыми переменными Расчет частных коэффициентов корреляции позволил получить следующие результаты наличие статистически значимой парной корреляционной связи между x 0 и x 1, что согласуется с естественным представлением о характере связей. Построение доверительных интервалов с использованием z-преобразования Фишера подтвердило полученные результаты
Пример 1 Искажающее влияние «третьего фактора» на корреляцию между двумя изучаемыми переменными Расчет частных коэффициентов корреляции позволил получить следующие результаты наличие статистически значимой парной корреляционной связи между x 0 и x 1, что согласуется с естественным представлением о характере связей. Построение доверительных интервалов с использованием z-преобразования Фишера подтвердило полученные результаты
 Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Пример 2. С целью исследования влияния погодных условий на урожайность кормовых трав были рассмотрены данные Министерства земледелия Англии за 20 лет, характеризующие x 0 -урожайность (в ц/акр) , x 1 - весеннее количество осадков (в дюймах) x 2 - накопленная за весну сумма температур, превышающих 5, 5 гр. (в градусах по Фаренгейту) По выборке были подсчитаны основные числовые характеристики трехмерной случайной величины:
Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Пример 2. С целью исследования влияния погодных условий на урожайность кормовых трав были рассмотрены данные Министерства земледелия Англии за 20 лет, характеризующие x 0 -урожайность (в ц/акр) , x 1 - весеннее количество осадков (в дюймах) x 2 - накопленная за весну сумма температур, превышающих 5, 5 гр. (в градусах по Фаренгейту) По выборке были подсчитаны основные числовые характеристики трехмерной случайной величины:
 Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Действительно ли высокая температура в период созревания трав (x 2) отрицательно влияет на их урожайность (коэф. отрицательный) или здесь сказывается опосредованное влияние «мешающего» фактора – количества осадков x 1 ? Частные коэффициенты корреляции составили: Если исключить одновременное влияние количества осадков на урожайность (с ростом x 1 она повышается) и на сумму активных температур (с ростом x 1 она понижается), то мы не обнаружим отрицательной корреляции между температурой и урожайностью.
Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Действительно ли высокая температура в период созревания трав (x 2) отрицательно влияет на их урожайность (коэф. отрицательный) или здесь сказывается опосредованное влияние «мешающего» фактора – количества осадков x 1 ? Частные коэффициенты корреляции составили: Если исключить одновременное влияние количества осадков на урожайность (с ростом x 1 она повышается) и на сумму активных температур (с ростом x 1 она понижается), то мы не обнаружим отрицательной корреляции между температурой и урожайностью.
 Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Построение доверительных интервалов для (с уровнем значимости р=0, 95) с использованием z-преобразования Фишера дало следующие результаты: Последнее неравенство свидетельствует о том, что нет оснований считать положительную очищенную корреляционную связь между урожайностью и температурой статистически значимой.
Трудности в интерпретации парных коэффициентов корреляции, связанные с опосредованным влиянием других переменных Построение доверительных интервалов для (с уровнем значимости р=0, 95) с использованием z-преобразования Фишера дало следующие результаты: Последнее неравенство свидетельствует о том, что нет оснований считать положительную очищенную корреляционную связь между урожайностью и температурой статистически значимой.
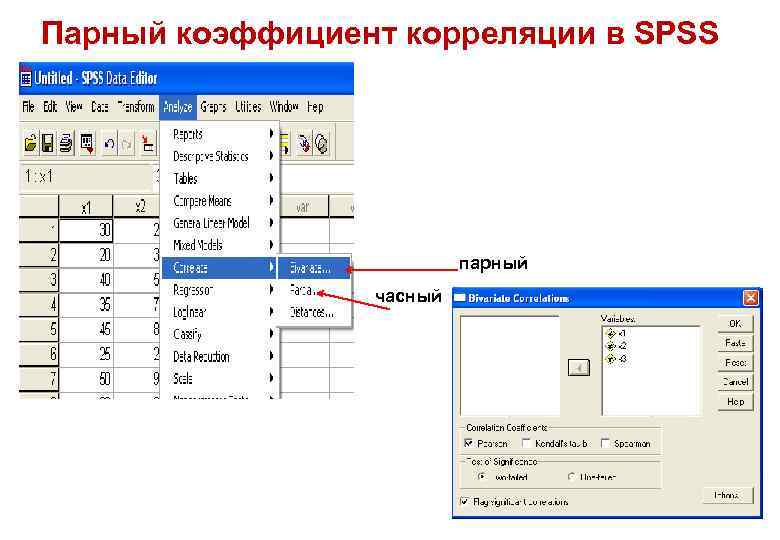 Парный коэффициент корреляции в SPSS парный часный
Парный коэффициент корреляции в SPSS парный часный
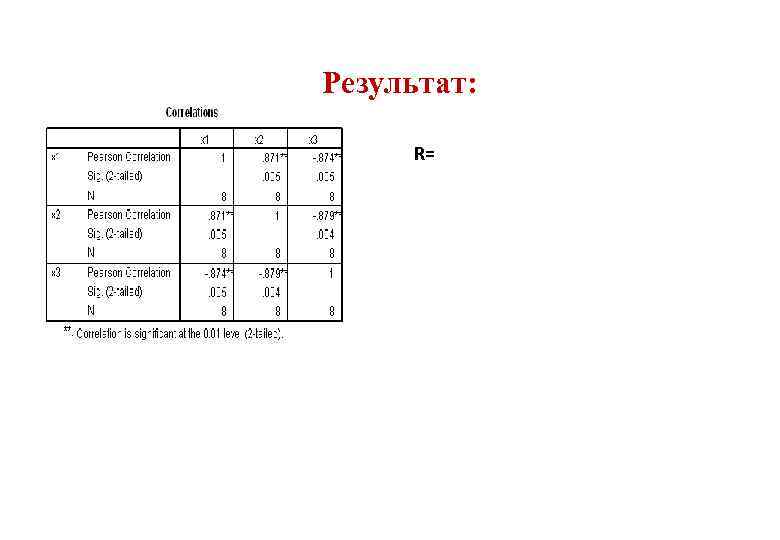 Результат: R=
Результат: R=
 Многомерный корреляционный анализ При исследование реальных экономических явлений приходится сталкиваться с анализом многомерной генеральной совокупности в которой каждый объект характеризуется набором признаков • Исследователь располагает случайной выборкой i= • Необходимо сделать вывод о параметрах р-мерной генеральной совокупности (многомерной случайной величине)
Многомерный корреляционный анализ При исследование реальных экономических явлений приходится сталкиваться с анализом многомерной генеральной совокупности в которой каждый объект характеризуется набором признаков • Исследователь располагает случайной выборкой i= • Необходимо сделать вывод о параметрах р-мерной генеральной совокупности (многомерной случайной величине)
 Многомерный корреляционный анализ Выводы основаны на информации, содержащейся в оценке • вектора математических ожиданий характеризует «центр тяжести» случайной выборки • ковариационной матрицы По существу вся специфика многомерной случайности сосредоточена в ковариационной матрице
Многомерный корреляционный анализ Выводы основаны на информации, содержащейся в оценке • вектора математических ожиданий характеризует «центр тяжести» случайной выборки • ковариационной матрицы По существу вся специфика многомерной случайности сосредоточена в ковариационной матрице
 Многомерный корреляционный анализ Ковариационная матрица позволяет строить и анализировать q характеристики вариации (рассеивания) q характеристики статистической взаимосвязи (коррелированности) компонент многомерного признака
Многомерный корреляционный анализ Ковариационная матрица позволяет строить и анализировать q характеристики вариации (рассеивания) q характеристики статистической взаимосвязи (коррелированности) компонент многомерного признака
 Многомерный корреляционный анализ Исходной для анализа является матрица: X= размерности (n x р), i-я строка которой характеризует i-е наблюдение (объект) по всем р - показателям (j=1, 2, . . . , р).
Многомерный корреляционный анализ Исходной для анализа является матрица: X= размерности (n x р), i-я строка которой характеризует i-е наблюдение (объект) по всем р - показателям (j=1, 2, . . . , р).
 Многомерная корреляционная модель Матрица парных коэффициентов корреляции R= Матрица R является симметричной и положительно определенной, на главной диагонали стоят единицы. Парный коэффициент корреляции, например, межу переменной x и y рассчитывается по формуле:
Многомерная корреляционная модель Матрица парных коэффициентов корреляции R= Матрица R является симметричной и положительно определенной, на главной диагонали стоят единицы. Парный коэффициент корреляции, например, межу переменной x и y рассчитывается по формуле:
 Многомерная корреляционная модель Матрица частных коэффициентов корреляции R= Матрица R является симметричной и положительно определенной, на главной диагонали стоят единицы.
Многомерная корреляционная модель Матрица частных коэффициентов корреляции R= Матрица R является симметричной и положительно определенной, на главной диагонали стоят единицы.
 Многомерная корреляционная модель Частный коэффициент корреляции в общем случае многомерной корреляционной модели показывает тесноту линейной зависимости между двумя рассматриваемыми переменными (например, x 1 и x 5) независимо от влияния остальных l (l=p-2) фиксируемых переменных. l где Rij – алгебраическое дополнение элемента rij корреляционной матрицы R
Многомерная корреляционная модель Частный коэффициент корреляции в общем случае многомерной корреляционной модели показывает тесноту линейной зависимости между двумя рассматриваемыми переменными (например, x 1 и x 5) независимо от влияния остальных l (l=p-2) фиксируемых переменных. l где Rij – алгебраическое дополнение элемента rij корреляционной матрицы R
 Многомерная корреляционная модель Частный коэффициент корреляции Для проверки значимости частного коэффициента корреляции используется те же критерии, что и для парного ρ, число степеней свободы - ν=n-l-2 Интервальная оценка для значимого частного коэффициента корреляции многомерной модели находится аналогично парному коэффициенту корреляции ρ, с помощью Z-преобразования Фишера, ΔZ рассчитывается по формуле:
Многомерная корреляционная модель Частный коэффициент корреляции Для проверки значимости частного коэффициента корреляции используется те же критерии, что и для парного ρ, число степеней свободы - ν=n-l-2 Интервальная оценка для значимого частного коэффициента корреляции многомерной модели находится аналогично парному коэффициенту корреляции ρ, с помощью Z-преобразования Фишера, ΔZ рассчитывается по формуле:
 Многомерная корреляционная модель Множественные коэффициенты корреляции и детерминации В общем случае многомерной корреляционной модели множественный коэффициент корреляции показывает тесноту связи между одной переменной и многомерным массивом остальных переменных где |R| - определитель, Аjl - алгебраическое дополнение элемента rjl корреляционной матрицы R.
Многомерная корреляционная модель Множественные коэффициенты корреляции и детерминации В общем случае многомерной корреляционной модели множественный коэффициент корреляции показывает тесноту связи между одной переменной и многомерным массивом остальных переменных где |R| - определитель, Аjl - алгебраическое дополнение элемента rjl корреляционной матрицы R.
 Многомерная корреляционная модель Множественные коэффициенты корреляции и детерминации Множественный коэффициент детерминации в общем случае многомерной корреляционной модели, например, R 23/1, 2, 4, …р (R 23) показывает долю дисперсии случайной величины X 3, обусловленную влиянием остальных переменных X 1, X 2, X 4, X 5, … Xр, включённых в корреляционную модель. Соответственно (1 - R 23) показывает долю остаточной дисперсии случайной величины X 3, обусловленную влиянием других, не включённых в корреляционную модель факторов
Многомерная корреляционная модель Множественные коэффициенты корреляции и детерминации Множественный коэффициент детерминации в общем случае многомерной корреляционной модели, например, R 23/1, 2, 4, …р (R 23) показывает долю дисперсии случайной величины X 3, обусловленную влиянием остальных переменных X 1, X 2, X 4, X 5, … Xр, включённых в корреляционную модель. Соответственно (1 - R 23) показывает долю остаточной дисперсии случайной величины X 3, обусловленную влиянием других, не включённых в корреляционную модель факторов
 Множественный коэффициент корреляции и его свойства 1. Множественный коэффициент корреляции изменяется в интервале 2. Минимальное значение соответствует случаю полного отсутствия корреляционной связи между η и остальными переменными. Это соответствует ситуации, когда усредненная дисперсия «регрессионных остатков» в точности равна общей вариации результирующего показателя.
Множественный коэффициент корреляции и его свойства 1. Множественный коэффициент корреляции изменяется в интервале 2. Минимальное значение соответствует случаю полного отсутствия корреляционной связи между η и остальными переменными. Это соответствует ситуации, когда усредненная дисперсия «регрессионных остатков» в точности равна общей вариации результирующего показателя.
 Множественный коэффициент корреляции и его свойства 3. Максимальное значение соответствует случаю полного отсутствия варьирования «регрессионных остатков» , что означает наличие функциональной связи между величиной η и остальными переменными. В этом случае мы имеем возможность точно восстановить условные значения η(X)={η/ξ=X} по значениям предикторных переменных X.
Множественный коэффициент корреляции и его свойства 3. Максимальное значение соответствует случаю полного отсутствия варьирования «регрессионных остатков» , что означает наличие функциональной связи между величиной η и остальными переменными. В этом случае мы имеем возможность точно восстановить условные значения η(X)={η/ξ=X} по значениям предикторных переменных X.
 Свойства множественного коэффициента корреляции 4. Множественный коэффициент корреляции превышает любой парный или частный коэффициент корреляции, характеризующий статистическую связь результирующего показателя. 5. Присоединение любой новой предсказывающей переменной не может уменьшить величины R (независимо от порядка присоединения).
Свойства множественного коэффициента корреляции 4. Множественный коэффициент корреляции превышает любой парный или частный коэффициент корреляции, характеризующий статистическую связь результирующего показателя. 5. Присоединение любой новой предсказывающей переменной не может уменьшить величины R (независимо от порядка присоединения).
 Свойства множественного коэффициента корреляции 6. Множественный коэффициент корреляции Rη может быть определен как максимальное значение обычного парного коэффициента корреляции между η и линейной комбинацией x 1, x 2, …, xp (максимум – по всевозможным линейным комбинациям) либо как обычный парный коэффициент корреляции между η и условным математическим ожиданием М(η/X).
Свойства множественного коэффициента корреляции 6. Множественный коэффициент корреляции Rη может быть определен как максимальное значение обычного парного коэффициента корреляции между η и линейной комбинацией x 1, x 2, …, xp (максимум – по всевозможным линейным комбинациям) либо как обычный парный коэффициент корреляции между η и условным математическим ожиданием М(η/X).
 Проверка значимости множественного коэффициента корреляции и детерминации Значимость множественного коэффициента корреляции (детерминации) проверяется с помощью F - критерия. 1. Наблюдаемое значение статистики находится по формуле:
Проверка значимости множественного коэффициента корреляции и детерминации Значимость множественного коэффициента корреляции (детерминации) проверяется с помощью F - критерия. 1. Наблюдаемое значение статистики находится по формуле:
 Проверка значимости множественного коэффициента корреляции 2. Нахождение критического значения статистики 3. Вывод по гипотезе Множественный коэффициент корреляции считается значимым, т. е. имеет место линейная статистическая зависимость, между X 1 и остальными факторами X 2, . . . , Xр, если: Fнабл. > Fкр. (α, р - 1, n – р).
Проверка значимости множественного коэффициента корреляции 2. Нахождение критического значения статистики 3. Вывод по гипотезе Множественный коэффициент корреляции считается значимым, т. е. имеет место линейная статистическая зависимость, между X 1 и остальными факторами X 2, . . . , Xр, если: Fнабл. > Fкр. (α, р - 1, n – р).
 Нелинейные связи • Рассмотрим фазовую плоскость (a, b), на которой крестиками нанесены одновременно принимаемые значения двух гипотетических переменных по результатам наблюдений. • Коэффициент линейной корреляции между a и b будет невысоким; однако едва ли найдется статистик, который стал бы утверждать, что эти параметры независимы. • В этом примере даже знак коэффициента корреляции будет определяться случайными обстоятельствами: их группировкой в зонах 1 и 3 (связь отрицательная). или в зонах 2 и 4 (связь положительная) Между тем, этот факт ничего не говорит о реальном характере взаимной зависимости переменных a и b.
Нелинейные связи • Рассмотрим фазовую плоскость (a, b), на которой крестиками нанесены одновременно принимаемые значения двух гипотетических переменных по результатам наблюдений. • Коэффициент линейной корреляции между a и b будет невысоким; однако едва ли найдется статистик, который стал бы утверждать, что эти параметры независимы. • В этом примере даже знак коэффициента корреляции будет определяться случайными обстоятельствами: их группировкой в зонах 1 и 3 (связь отрицательная). или в зонах 2 и 4 (связь положительная) Между тем, этот факт ничего не говорит о реальном характере взаимной зависимости переменных a и b.
 Нелинейные связи • Перед построением регрессионных моделей необходимо исследовать причинные связи в экономике! • Нобелевский лауреат Морис Аллэ много раз высказывал скептическое отношение к регрессионным моделям, построенным наобум, а злоупотребление ими в обстоятельствах, не вызывающих к ним серьезного доверия, называл «дикой эконометрикой» . • Он являлся сторонником параметрических моделей, в которых характер взаимосвязи между рассматриваемыми переменными выявляется заранее на основе анализа их фактически наблюдаемых значений. 1. Алле М. Философия моей жизни [http: //lib. ixbt. by/economics/ixbt_show _archives. php? subaction=showfull&id=1100489557&archive=1120044401&start_from=&ucat=1&]
Нелинейные связи • Перед построением регрессионных моделей необходимо исследовать причинные связи в экономике! • Нобелевский лауреат Морис Аллэ много раз высказывал скептическое отношение к регрессионным моделям, построенным наобум, а злоупотребление ими в обстоятельствах, не вызывающих к ним серьезного доверия, называл «дикой эконометрикой» . • Он являлся сторонником параметрических моделей, в которых характер взаимосвязи между рассматриваемыми переменными выявляется заранее на основе анализа их фактически наблюдаемых значений. 1. Алле М. Философия моей жизни [http: //lib. ixbt. by/economics/ixbt_show _archives. php? subaction=showfull&id=1100489557&archive=1120044401&start_from=&ucat=1&]
 Корреляционное отношение. Исследование парных нелинейных связей При отклонении исследуемых зависимостей от линейного вида, коэффициент корреляции теряет свой смысл как характеристика степени тесноты связи. Корреляционное соотношение (КО)- характеристика тесноты связи между x и y в случае нелинейной зависимости. КО используется тогда, когда характер выборки (x 1, y 1), (x 2, y 2), …, (xn, yn) допускает их группировку по оси объясняющей переменной x и подсчет частных средних внутри каждого j-го интервала группирования. где j=1, 2, …, m и m - число интервалов группирования; nj – число наблюдений (точек) в j-м интервале.
Корреляционное отношение. Исследование парных нелинейных связей При отклонении исследуемых зависимостей от линейного вида, коэффициент корреляции теряет свой смысл как характеристика степени тесноты связи. Корреляционное соотношение (КО)- характеристика тесноты связи между x и y в случае нелинейной зависимости. КО используется тогда, когда характер выборки (x 1, y 1), (x 2, y 2), …, (xn, yn) допускает их группировку по оси объясняющей переменной x и подсчет частных средних внутри каждого j-го интервала группирования. где j=1, 2, …, m и m - число интервалов группирования; nj – число наблюдений (точек) в j-м интервале.
 Корреляционное отношение. Исследование парных нелинейных связей Тогда межгрупповая вариация y характеризуется дисперсией Общая выборочная дисперсия yji относительно общей средней равна
Корреляционное отношение. Исследование парных нелинейных связей Тогда межгрупповая вариация y характеризуется дисперсией Общая выборочная дисперсия yji относительно общей средней равна
 Корреляционное отношение. Исследование парных нелинейных связей квадрат КО переменной x равно: зависимой переменной y по независимой Его вычисление не связано с видом уравнения регрессии. В отличие от парного коэффициента корреляции r КО несимметрично по отношению к исследуемым переменным, то есть в общем случае
Корреляционное отношение. Исследование парных нелинейных связей квадрат КО переменной x равно: зависимой переменной y по независимой Его вычисление не связано с видом уравнения регрессии. В отличие от парного коэффициента корреляции r КО несимметрично по отношению к исследуемым переменным, то есть в общем случае
 Корреляционное отношение. Исследование парных нелинейных связей КО, по определению, величина неотрицательная как положительный корень из Из следует наличие однозначной функциональной связи между y и x и, наоборот, из функциональной связи между y и x следует, что. Отсутствие связи между y и x означает, что условные средние равны между собой и равны , поэтому и наоборот, если , то и следовательно частные средние не зависят от x. Отметим, что между нет никакой простой зависимости.
Корреляционное отношение. Исследование парных нелинейных связей КО, по определению, величина неотрицательная как положительный корень из Из следует наличие однозначной функциональной связи между y и x и, наоборот, из функциональной связи между y и x следует, что. Отсутствие связи между y и x означает, что условные средние равны между собой и равны , поэтому и наоборот, если , то и следовательно частные средние не зависят от x. Отметим, что между нет никакой простой зависимости.
 Корреляционное отношение. Исследование парных нелинейных связей В случае линейной зависимости и совпадают, поэтому статистику используют в качестве меры отклонения регрессионной зависимости от линейного вида.
Корреляционное отношение. Исследование парных нелинейных связей В случае линейной зависимости и совпадают, поэтому статистику используют в качестве меры отклонения регрессионной зависимости от линейного вида.
 Корреляционное отношение. Исследование парных нелинейных связей Для проверки значимости , то есть проверки при заданном гипотезы используют F- критерий, основанный на статистике которую сравнивают с табличными значениями Если , то с вероятностью ошибки утверждают, что зависимость между переменными существует, в противном случае не отвергается.
Корреляционное отношение. Исследование парных нелинейных связей Для проверки значимости , то есть проверки при заданном гипотезы используют F- критерий, основанный на статистике которую сравнивают с табличными значениями Если , то с вероятностью ошибки утверждают, что зависимость между переменными существует, в противном случае не отвергается.
 Ложная корреляция Пример Пожары - положительная корреляция между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара. ? ? вывод «бо льшее количество пожарных приводит к бо льшему ущербу» → минимизировать ущерб от пожаров путем ликвидации пожарных бригад? ? ? Пример 2: Корреляция между размером обуви и средним доходом человека. ? ? нося обувь на размер больше, вы станете (получите шанс) больше зарабатывать? ? ?
Ложная корреляция Пример Пожары - положительная корреляция между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара. ? ? вывод «бо льшее количество пожарных приводит к бо льшему ущербу» → минимизировать ущерб от пожаров путем ликвидации пожарных бригад? ? ? Пример 2: Корреляция между размером обуви и средним доходом человека. ? ? нося обувь на размер больше, вы станете (получите шанс) больше зарабатывать? ? ?


