 Корреляционный и регрессионный анализ Основная задача статистики – обнаружить связь между явлениями, её вид и дать количественную характеристику этой связи. Вид связи между явлениями
Корреляционный и регрессионный анализ Основная задача статистики – обнаружить связь между явлениями, её вид и дать количественную характеристику этой связи. Вид связи между явлениями
 Предмет корреляционно-регрессионного анализа составляет исследование статистических зависимостей между явлениями Корреляционный анализ Регрессионный анализ
Предмет корреляционно-регрессионного анализа составляет исследование статистических зависимостей между явлениями Корреляционный анализ Регрессионный анализ
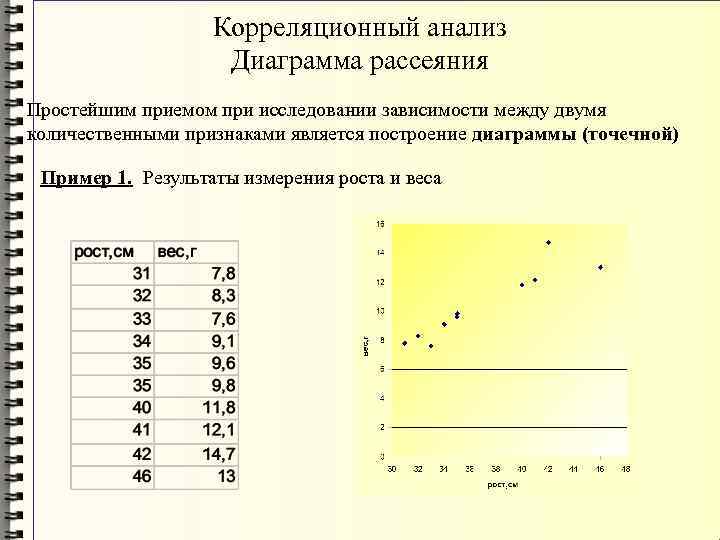 Корреляционный анализ Диаграмма рассеяния Простейшим приемом при исследовании зависимости между двумя количественными признаками является построение диаграммы (точечной) Пример 1. Результаты измерения роста и веса
Корреляционный анализ Диаграмма рассеяния Простейшим приемом при исследовании зависимости между двумя количественными признаками является построение диаграммы (точечной) Пример 1. Результаты измерения роста и веса
 Линейный коэффициент корреляции Пирсона Основные свойства коэффициента корреляции: Нет линейной связи
Линейный коэффициент корреляции Пирсона Основные свойства коэффициента корреляции: Нет линейной связи
 Линейный коэффициент корреляции Пирсона
Линейный коэффициент корреляции Пирсона
 Линейный коэффициент корреляции Пирсона Пример 2. Рейтинг и пропуски Число пропусков занятий, x 6 2 15 9 12 5 8 Итоговый рейтинг, y 82 86 43 74 58 90 78
Линейный коэффициент корреляции Пирсона Пример 2. Рейтинг и пропуски Число пропусков занятий, x 6 2 15 9 12 5 8 Итоговый рейтинг, y 82 86 43 74 58 90 78
 Линейный коэффициент корреляции Пирсона Пример 3. Возраст курящих и количество сигарет, выкуриваемых в день Возраст курящего, x 27 64 36 42 31 18 53 64 58 25 Число сигарет в день, y 6 10 9 18 7 12 5 12 7 3
Линейный коэффициент корреляции Пирсона Пример 3. Возраст курящих и количество сигарет, выкуриваемых в день Возраст курящего, x 27 64 36 42 31 18 53 64 58 25 Число сигарет в день, y 6 10 9 18 7 12 5 12 7 3
 Проверка значимости коэффициента корреляции Критерий Стьюдента для коэффициента корреляции: tкрит --- СТЬЮДРАСПОБР ( ; n-2) Корреляция значима, когда t >tкрит
Проверка значимости коэффициента корреляции Критерий Стьюдента для коэффициента корреляции: tкрит --- СТЬЮДРАСПОБР ( ; n-2) Корреляция значима, когда t >tкрит
 Коэффициент ранговой корреляции Спирмена Расчет: 1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле: где -сумма квадратов разностей рангов, а n- число парных наблюдений.
Коэффициент ранговой корреляции Спирмена Расчет: 1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле: где -сумма квадратов разностей рангов, а n- число парных наблюдений.
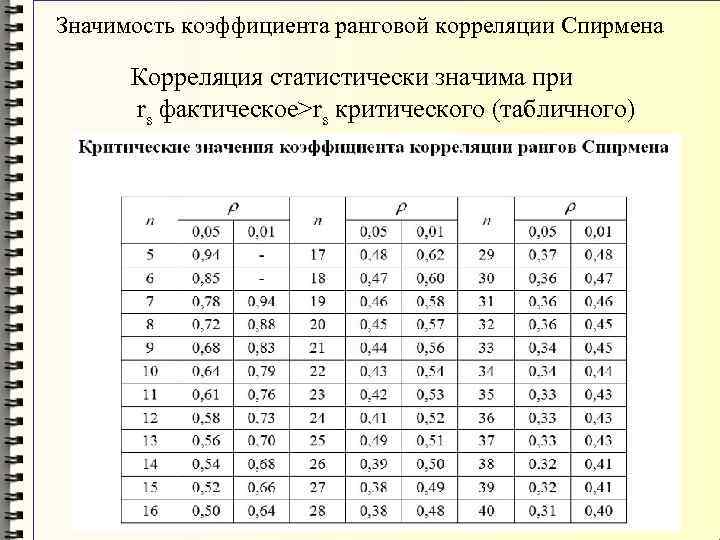 Значимость коэффициента ранговой корреляции Спирмена Корреляция статистически значима при rs фактическое>rs критического (табличного)
Значимость коэффициента ранговой корреляции Спирмена Корреляция статистически значима при rs фактическое>rs критического (табличного)
 время, мин, x 27 64 36 42 31 18 активность фермента, у. е. у 6 4 5 3 5 12 Ранги x 2 7 4 5 3 1 Ранги y 6 2 3 1 3 7 r. S= -0, 83
время, мин, x 27 64 36 42 31 18 активность фермента, у. е. у 6 4 5 3 5 12 Ранги x 2 7 4 5 3 1 Ранги y 6 2 3 1 3 7 r. S= -0, 83
 Проверка значимости коэффициента ранговой корреляции. Спирмена При n>40 следует применять к. Стюдента для проверки значимости tкрит --- СТЬЮДРАСПОБР ( ; n-2) Корреляция значима, когда t >tкрит
Проверка значимости коэффициента ранговой корреляции. Спирмена При n>40 следует применять к. Стюдента для проверки значимости tкрит --- СТЬЮДРАСПОБР ( ; n-2) Корреляция значима, когда t >tкрит