Корреляционный анализ Виды и формы связей между явлениями

Корреляционный анализ Виды и формы связей между явлениями.

Три типа взаимосвязей между различными явлениями и их признаками: Функциональная связь – это вид причинной зависимости, при которой определенному значению факторного признака (x) соответствует только одно точно заданное значение результативного признака (y). Нпр. Алгебраические функции. 2. Статистическая связь – это вид причинной зависимости, проявляющейся не в каждом отдельном случае, а в общем, при большом числе наблюдений. Нпр. Зависимость роста детей от роста родителей; потребление продуктов питания от душевого дохода. 1.

Корреляционная связь – это зависимость среднего значения результативного признака (у) от изменения факторного признака (х); в то время как каждому отдельному факторному признаку может соответствовать множество различных значений результативного. Задачи корреляционного анализа: 1. Изучение степени тесноты связи двух и более явлений; 2. Отбор факторов, оказывающих наиболее существенное влияние на результативный признак; 3. Выявление неизвестных причинных связей 3.

Этапы исследования корреляционных зависимостей: 1. Предварительный анализ свойств совокупности; 2. Установление факта наличия связи, определение ее направления (прямая и обратная) и формы (прямолинейная и нелинейная); 3. Измерение степени тесноты связи между признаками; 4. Построение регрессионной модели, т. е. нахождение аналитического выражения связи; 5. Оценка адекватности модели, ее экономическую интерпретацию и практическое использование.

Пути возникновения корреляционной зависимости: Причинная зависимость результативного признака от вариации факторного признака, например: Х – балл оценки плодородия почвы; У – урожайность сельскохозяйственной культуры. Возникновение связи между двумя следствиями общей причины (ложная корреляция), например: 17 августа 1998 г. Резко возросла цена валюты и объем покупки валюты частными лицами. Общая причина – обострение финансового кризиса. Если каждый из признаков и причина и следствие, например: производительность труда и заработная плата.

Предварительный анализ свойств совокупности и установление факта наличия связи, определение ее направления (прямая и обратная) и формы (прямолинейная и нелинейная). 1. Приведение параллельных данных. Х 1 2 3 4 5 6 7 8 9 У 5 9 6 10 12 17 15 20 23 2. Аналитических группировок.

3. Графический. 14 12 10 8 Значения Y 6 4 2 0 0 1 2 3 4 5 6

Измерение степени тесноты связи между признаками Показатель Фехнера Х 1 2 3 4 5 6 7 8 9 У 5 9 6 10 12 17 15 20 23 -4 -3 -2 -1 0 1 2 3 4 -8 -4 -7 -3 -1 4 2 7 10

Коэффициент корреляции – показатель интенсивности линейной связи:

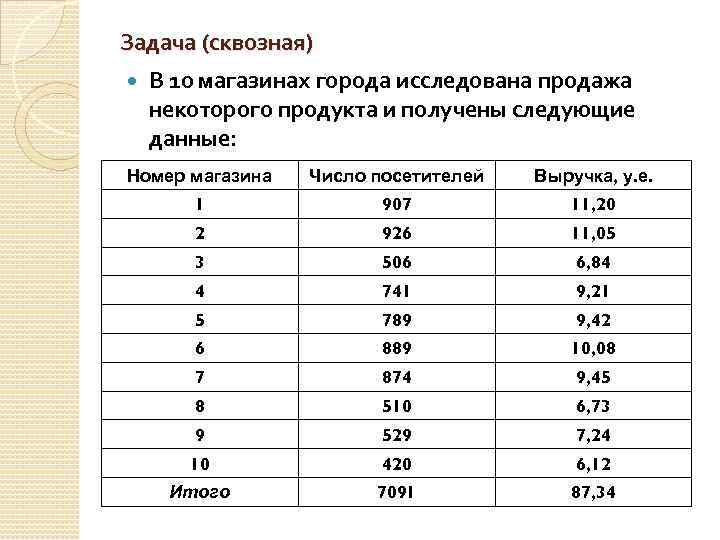Задача (сквозная) В 10 магазинах города исследована продажа некоторого продукта и получены следующие данные: Номер магазина Число посетителей Выручка, у. е. 1 907 11, 20 2 926 11, 05 3 506 6, 84 4 741 9, 21 5 789 9, 42 6 889 10, 08 7 874 9, 45 8 510 6, 73 9 529 7, 24 10 420 6, 12 Итого 7091 87, 34

Провести предварительный анализ свойств совокупности. Измерить степень тесноты связи между признаками, используя коэффициент корреляции. Решение: 1. Приведение параллельных данных. X 907 926 506 741 789 874 510 529 420 Y 11, 20 11, 05 6, 84 9, 21 9, 42 10, 08 9, 45 6, 73 7, 24 6, 12 2. Метод аналитических группировок.

3. Графический Выручка 11. 2 9. 21 6. 84 6. 73 510 529 9. 45 741 789 874 907 926 10. 08 6. 78 506 9. 42 11. 05 889

Линейный коэффициент корреляции

Выборочные средние:

4. Расчет коэффициента корреляции Мага зин Число покуп ателе й Х Выру чка 1 907 11, 20 2 926 11, 05 3 506 6, 84 4 741 9, 21 5 789 9, 42 6 889 10, 08 7 874 9, 45 8 510 6, 73 9 529 7, 24 10 420 6, 12 Итог: 7091 87, 34 У

Мага зин Число покуп ателе й Х Выру чка 1 907 11, 20 198 2, 47 489, 06 39204 6, 1 2 926 11, 05 217 2, 32 503, 44 47089 5, 38 3 506 6, 84 -203 -1, 89 383, 67 41209 3, 57 4 741 9, 21 32 0, 48 15, 36 1024 0, 23 5 789 9, 42 80 0, 69 55, 2 6400 0, 48 6 889 10, 08 180 1, 35 243, 0 32400 1, 82 7 874 9, 45 165 0, 73 120, 45 27225 0, 52 8 510 6, 73 -199 -2 398, 0 39601 4 9 529 7, 24 -180 -1, 49 268, 2 32400 2. 22 10 420 6, 12 -289 -2, 61 754, 29 83521 6, 81 Итог: 7091 87, 34 3230, 67 350073 31, 13 У

Ранговая корреляция Ранг – это ранжирование объектов по определенному признаку. Например: при выяснении предпочтений потребителей при выборе товара.

Задача. Пусть имеется 5 продуктов, расположенных по порядку предпочтений от 1 до 5 в соответствии с двумя характеристиками: Характеристик и для ранжирования V W X Y Z А 2 5 1 3 4 В 1 3 2 4 5 Продукт

Коэффициент ранговой корреляции Спирмена

Задача Семь вновь принятых сотрудников брокерской компании проходят аттестацию в конце испытательного периода. Результаты их работы оцениваются путем сдачи теста на профессиональную пригодность и по отдаче с каждого инвестированного рубля: Молоды е специал исты А В С Д Е F G Результ ат теста 3 2 6 4 1 7 5 Отдача с рубля 1 3 5 2 4 6 7

Оценка уравнения парной регрессии Регрессия – это односторонняя статистическая зависимость. Уравнение регрессии позволяет определить, каким в среднем будет значение результативного признака (У) при том или ином значении факторного признака (Х), если на остальные факторы не обращать внимания.

Виды уравнений парной регрессии:

Парная линейная зависимость

Метод наименьших квадратов Минимум суммы квадратов отклонений теоретических значений результативного признака от эмпирических имеет вид:

Система нормальных уравнений:

№ Х У 1 907 11, 20 2 926 11, 05 3 506 6, 84 4 741 9, 21 5 789 9, 42 6 889 10, 08 7 874 9, 45 8 510 6, 73 9 529 7, 24 10 420 6, 12 итого 7091 87, 34 ХУ

№ Х У ХУ 1 907 11, 20 822649 10158, 4 2 926 11, 05 857476 10232, 3 3 506 6, 84 256036 3461, 04 4 741 9, 21 549081 6824, 61 5 789 9, 42 622521 7432, 38 6 889 10, 08 790321 8961, 12 7 874 9, 45 763876 8259, 3 8 510 6, 73 260100 3432, 3 9 529 7, 24 279841 3829, 96 10 420 6, 12 176400 2570, 4 итого 7091 87, 34 5378301 65161, 81

Решить систему методом Крамера

Выводы: ü Минимальная сумма продаж составляет – 2, 19 у. е. ; ü Каждый человек увеличивает выручку магазина, в среднем, на 0, 009 у. е.

Интерпретация параметров уравнения регрессии параметры знак выводы b 0 b 1 + + Y – min b 0 b 1 + - b 0 b 1 + на каждую единицу X фактор Y увеличивается на b 1 единиц Y – max на каждую единицу X фактор Y уменьшается на b 1 единиц на каждую единицу X фактор Y увеличивается на b 1 единиц