Корреляционной анализ. Функциональная и стохастическая зависимости Корреляция, корреляционное

Корреляционной анализ

Функциональная и стохастическая зависимости Корреляция, корреляционное поле. Прямая и обратная корреляция Парный и ранговый коэффициенты корреляции Определение значимости коэффициента корреляции

В математике существуют два подхода к анализу тесноты связи Функциональная зависимость – такой вид связи между двумя признаками X и Y, при которой каждому значению одного из них соответствует одно и только одно значение другого. Например: ПС = ЧСС/V1м; S = V * t Стохастическая или вероятностная зависимость – такая форма связи, когда при фиксированном значении одной величины другая величина может принимать различные значения.

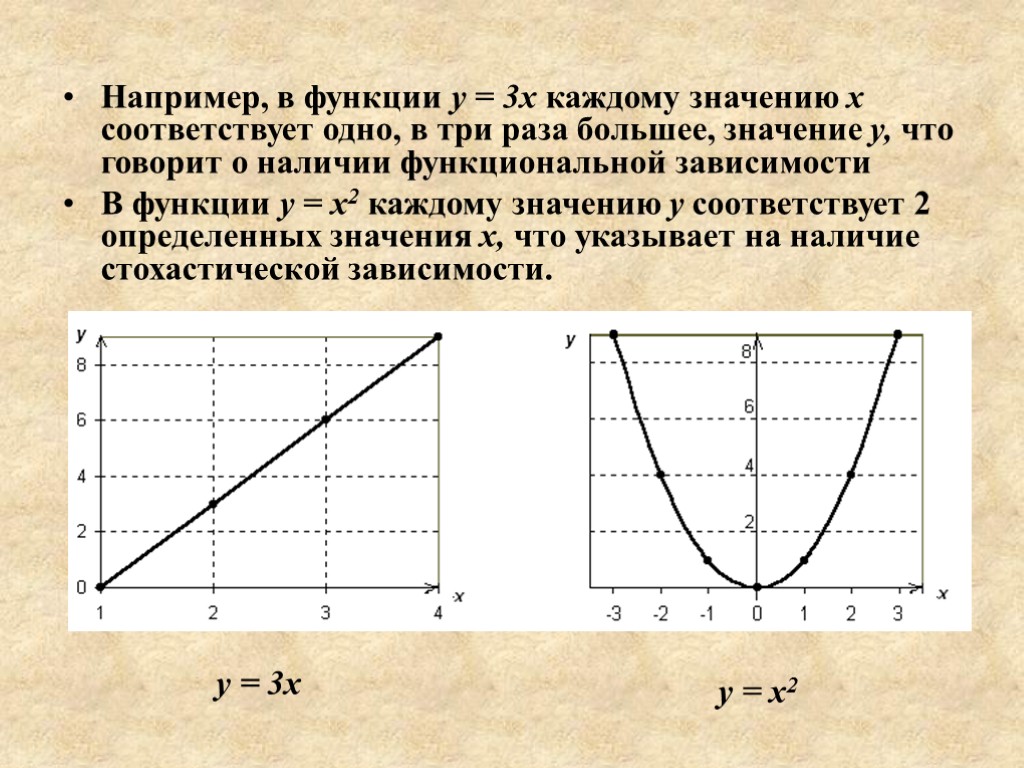
у = 3х Например, в функции у = 3х каждому значению х соответствует одно, в три раза большее, значение y, что говорит о наличии функциональной зависимости В функции у = х2 каждому значению у соответствует 2 определенных значения х, что указывает на наличие стохастической зависимости. у = х2

Корреляция (от латинского correlatio соотношение, связь) – зависимость между двумя случайными величинами X и Y, которая характеризуется специальными коэффициентами Корреляционный анализ состоит в определении связи между двумя случайными величинами Х и У, где в качестве меры связи используется коэффициент корреляции По своему характеру корреляция бывает прямая (положительная) и обратная (отрицательная). Прямая корреляция – с увеличением первого признака второй тоже увеличивается (соответственно, с уменьшением – уменьшается). Обратная корреляция – уменьшение второго признака с увеличением первого (и, наоборот, увеличение второго с уменьшением первого)

Графическая интерпретация – корреляционное поле Если точки рассеяны хаотично, то связь между признаками отсутствует. Если точки группируются вокруг какой-либо линии, то связь есть, и она тем теснее, чем ближе они группируются. По направлению линии можно сделать вывод о том, положительная или отрицательная корреляция.

Для количественной оценки корреляционной зависимости применяют коэффициент корреляции.

ПАРНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ БРАВЕ - ПИРСОНА Если 0 < rxy < =0,39 – связь слабая. Если 0,4 <= rxy <= 0,69 – связь средняя. Если 0,7 < =rxy < = 0,99 – связь тесная Если rxy = 0 – корреляция отсутствует. Если rxy = 1 – связь функциональная. Знак коэффициента корреляции указывает на направление связи («+» - связь прямая, «-» - обратная)

ПРИМЕР 4.2. Оценить существует ли взаимосвязь между упражнением прыжок в высоту с места и результатом в толчке штанги для тяжелоатлетов (возраст – 12 лет, весовая категория – до 60 кг.) Исходные данные: прыжок в высоту с места(см): 57, 60, 58, 61, 63, 68, 55, 64, 65, 64, 66, 61 толчок (кг): 107,5 110 110 115 115 107,5 107,5 120 112,5 122,5 120, 110

Алгоритм решения Методом средних величин находим средние арифметические признаков Х (прыжок) и Y (толчок): = 61 (см) и = 113 (кг) Находим разности между средними арифметическими и отдельными значениями признаков (для Х и У отдельно), возводим эти разности в квадраты и находим соответствующие суммы для подстановки в формулу для расчета коэффициента rxy: = 177,5 ( это сумма произведений разностей); = 134 ( это сумма квадратов разностей первого признака); = 311,3 ( это сумма квадратов разностей второго признака).

3. Подставляем найденные суммы в формулу для расчета коэффициента и находим коэффициент корреляции rxy : 4. Вывод: так как коэффициент корреляции равен 0,87, то связь между признаками сильная и прямая, т.е. результат в толчке у тяжелоатлетов зависит от специальных упражнений (прыжок в высоту с места).

РАНГОВЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ СПИРМЕНА Применяется в том случае, когда значения признаков заданы в порядковой шкале (оценки судей в баллах, места на соревнованиях и пр.) где – это разности рангов i-й пары значений Xi и Yi, n – объем выборки ( количество пар)

Ранговый коэффициент корреляции обладает теми же свойствами, что и парный Ранг – порядковый номер выборочного значения, если в выборке нет совпадающих значений Если же они есть, то ранг определяется как среднее арифметическое порядковых номеров совпадающих значений В данном методе присваивают ранги, начиная с лучшего результата

ПРИМЕР. Существует ли связь между результатами в прыжках в длину с места - xi (cм) и занятыми на соревнованиях местами – yi для гимнастов 11-12 лет. Алгоритм решения. Находим ранги Rxi и Ryi значений Xi и Yi , (они приведены в столбцах 4 и 5 таблицы). Вычисляем разности рангов Di = Rxi - Ryi( столбец 6). Возводим разности в квадрат (столбец 7) и находим сумму : По формуле определяем ранговый коэффициент корреляции:

Вывод: полученный коэффициент корреляции свидетельствует об отсутствии статистически значимой корреляционной зависимости между результатами гимнастов 11-12 лет в прыжках с места и местами, занятыми на соревнованиях.

Определение значимости коэффициента корреляции Для проверки значимости коэффициента корреляции, задаем значение доверительной вероятности, например Р=0,95 (или уровень значимости р=0,05), находим по таблице значение критического (граничного) значения критерия Стьюдента tкр и сравниваем его с расчетным значением tр , которое определяется по формуле Если tp > tkp, т. е. происходит маловероятное событие, предположение о некоррелированности признаков необоснованно и коэффициент корреляции считается значимым. Если же tp < tkp, коэффициент корреляции считается незначимым.