Коррекция ИХ и ЧХ ЦФ с помощью весовой

Коррекция ИХ и ЧХ ЦФ с помощью весовой обработки взвешиванием Применение окон

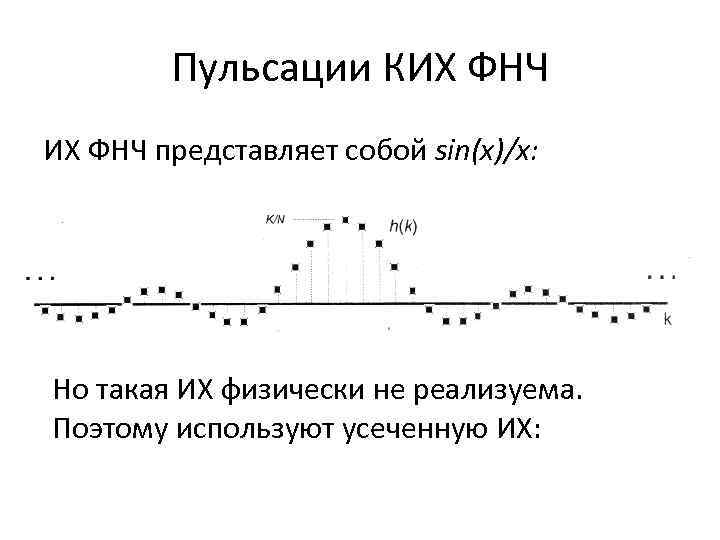Пульсации КИХ ФНЧ представляет собой sin(x)/x: Но такая ИХ физически не реализуема. Поэтому используют усеченную ИХ:

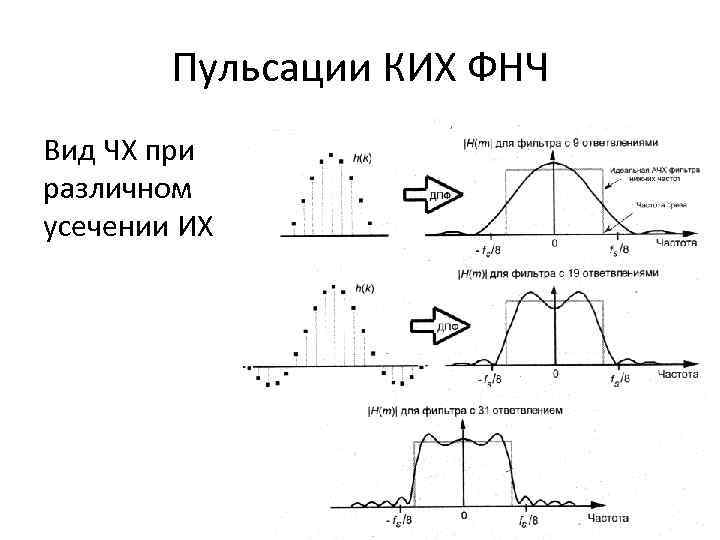Пульсации КИХ ФНЧ Вид ЧХ при различном усечении ИХ

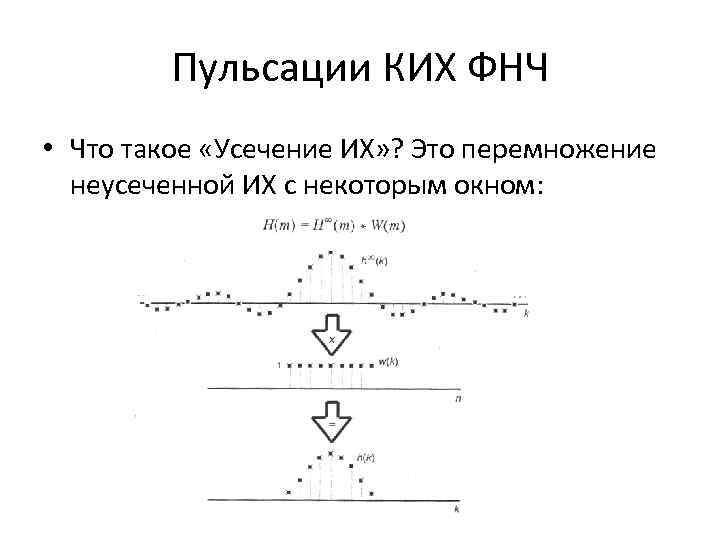Пульсации КИХ ФНЧ • Что такое «Усечение ИХ» ? Это перемножение неусеченной ИХ с некоторым окном:

Пульсации КИХ ФНЧ С учетом получим: итоговая ЧХ равна произведению ЧХ идеального фильтра на ЧХ окна усечения. Пульсации H(m) вызваны боковыми лепестками W(m).

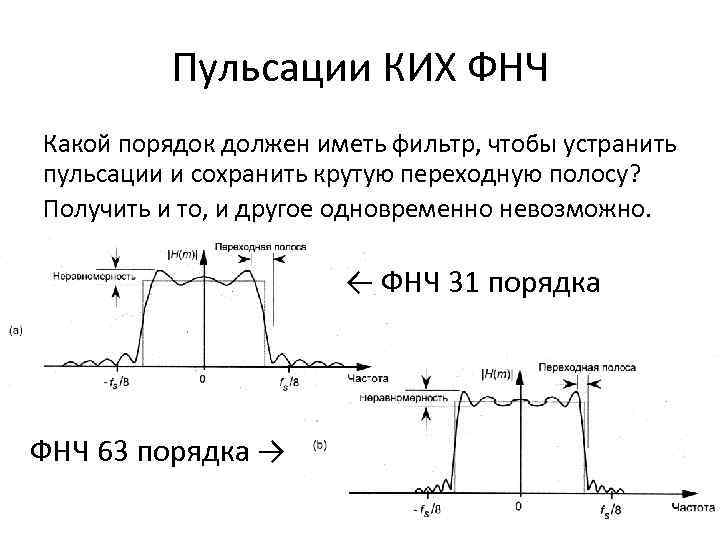Пульсации КИХ ФНЧ Какой порядок должен иметь фильтр, чтобы устранить пульсации и сохранить крутую переходную полосу? Получить и то, и другое одновременно невозможно. ← ФНЧ 31 порядка ФНЧ 63 порядка →

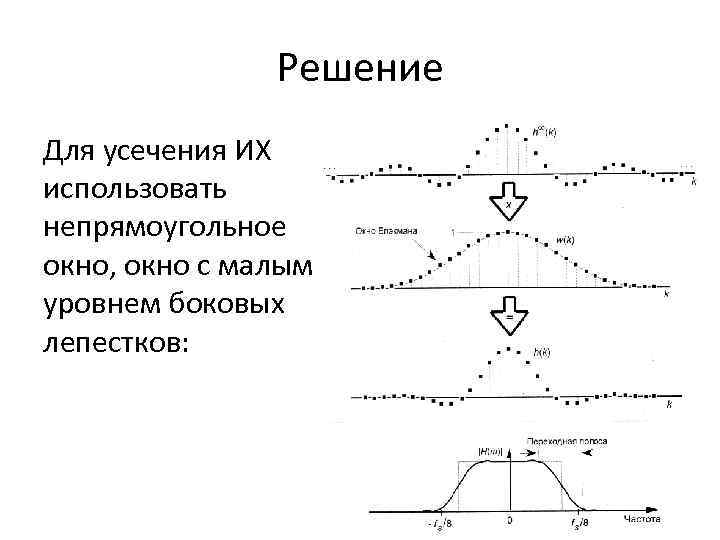Решение Для усечения ИХ использовать непрямоугольное окно, окно с малым уровнем боковых лепестков:

Применение окон Для снижения уровня боковых лепестков используют весовую обработку входной последовательности xk, которая состоит в ее умножении на некоторую временную функцию ( «весовое окно» , «Window» ) W(k). Эта функция близка к единице в середине и плавно убывает к краям.

Применение окон Во временной области умножение на плавно спадающую к краям функцию уменьшает скачки сигнала на краях выборки, соответственно уменьшается уровень гармоник, связанных с этими скачками. В результате форма ИХ становится более плавной.

Применение окон В спектральной области перемножению выборки и весовой функции соответствует свёртка спектров сигнала и весовой функции. Частотная характеристика при этом имеет вид

Применение окон Подбирая весовую функцию, можно уменьшить уровень боковых лепестков, однако при этом: • несколько расширяется главный лепесток спектра; • по обе стороны от точек разрыва появляются переходные полосы, ширина которых зависит от ширины главного лепестка функции W(k); • на всех частотах появляются ошибки аппроксимации (пульсации частотной характеристики), обусловленные боковыми лепестками функции W(k).

Применение окон Таким образом, временное окно должно удовлетворять следующим требованиям: 1. Ширина главного лепестка, в котором сосредоточена основная часть энергии, должна быть малой; 2. Энергия боковых лепестков должна быстро уменьшаться при

Применение окон Известно большое число разновидностей весовых окон. Выбор типа окна зависит от назначения фильтра, сложности расчета весовых коэффициентов и так далее.

Треугольное окно Отсчеты треугольного окна рассчитываются по следующей формуле:

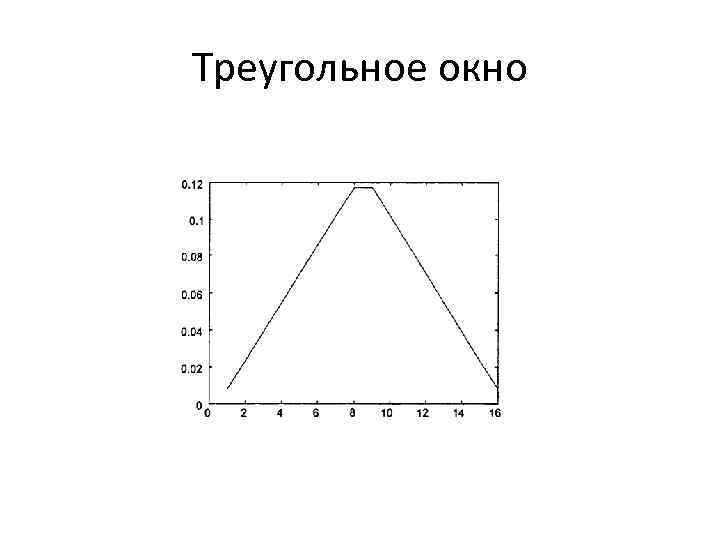Треугольное окно

Окно Бартлетта

Окно Бартлетта В отличие от треугольного окна, значения окна Бартлетта по краям равны нулю. Кроме того, это окно является симметричным независимо от четности. Окно Бартлетта представляет собой отсчеты симметричного треугольного импульса, который начинается при k=1, заканчивается при k=N и имеет единичную амплитуду. При нечетном N: • окно не достигает единичного значения в середине; • ненулевые отсчеты совпадают с отсчетами треугольного окна длины N-2.

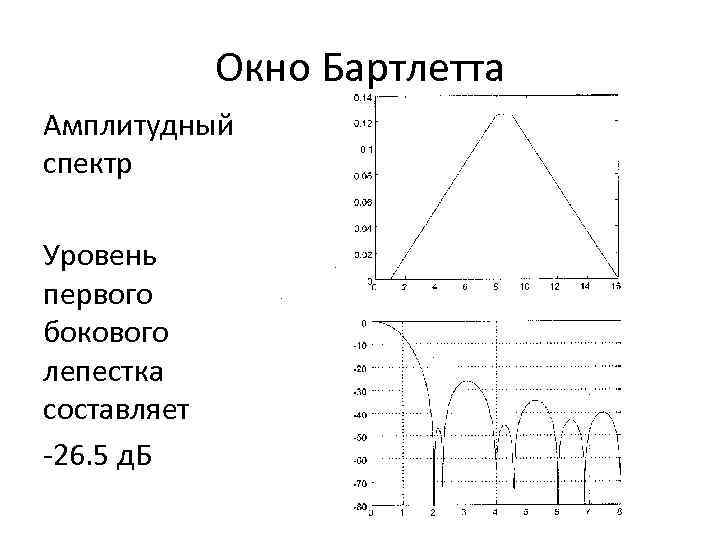Окно Бартлетта Амплитудный спектр Уровень первого бокового лепестка составляет -26. 5 д. Б

Окно Ханна В симметричном случае отсчеты окна Ханна рассчитываются по формуле

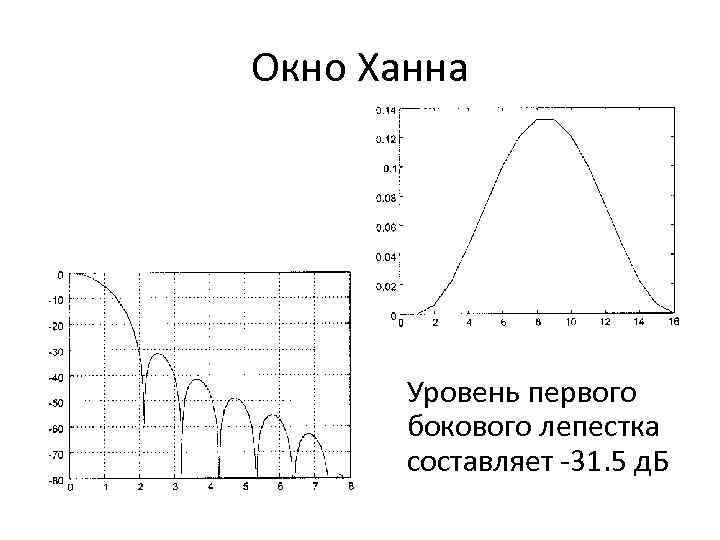Окно Ханна Уровень первого бокового лепестка составляет -31. 5 д. Б

Окно Хэмминга В симметричном случае отсчеты окна Хэмминга рассчитываются по формуле

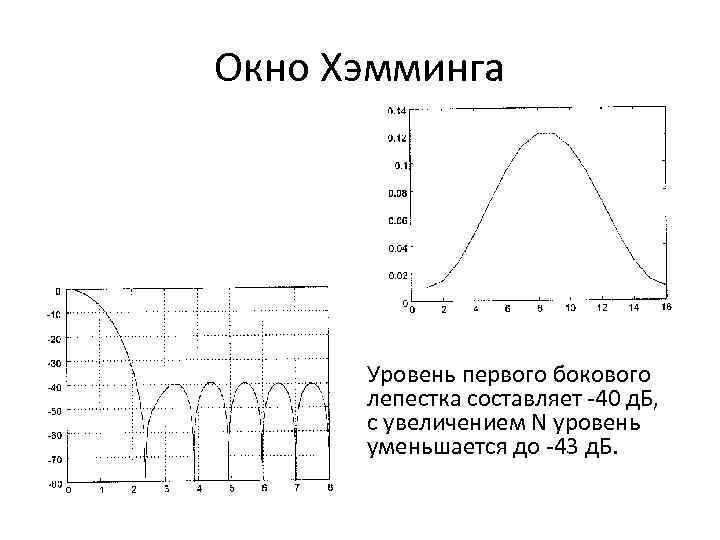Окно Хэмминга Уровень первого бокового лепестка составляет -40 д. Б, с увеличением N уровень уменьшается до -43 д. Б.

Окно Кайзера Отсчеты окна Кайзера рассчитываются по формуле Здесь I 0 – модифицированная функция Бесселя первого рода нулевого порядка. Чем больше β, тем больше энергия, сосредоточенная в главном лепестке, и ширина этого лепестка; и тем ниже уровень боковых лепестков. Применяются β от 4 до 9.

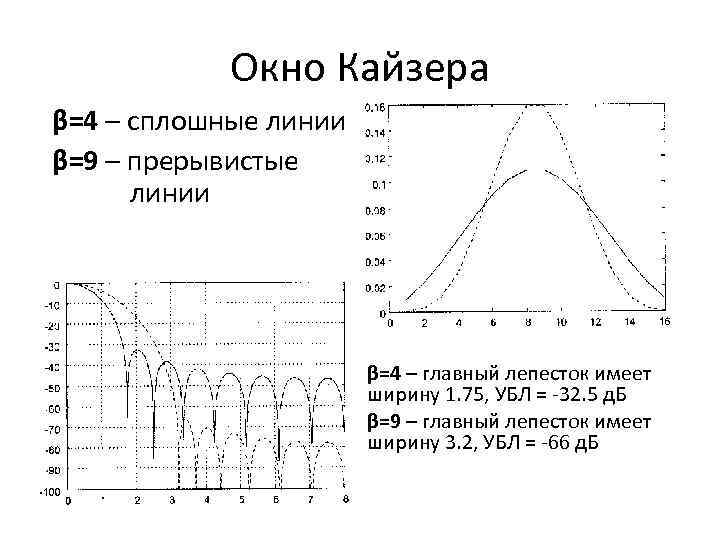Окно Кайзера β=4 – сплошные линии β=9 – прерывистые линии β=4 – главный лепесток имеет ширину 1. 75, УБЛ = -32. 5 д. Б β=9 – главный лепесток имеет ширину 3. 2, УБЛ = -66 д. Б

Окно Чебышева Для окна Чебышева все боковые лепестки имеют одинаковый, заданный при расчете окна уровень. Отсчеты окна Чебышева рассчитываются путем вычисления ОПФ от его ЧХ: Здесь β – степень подавления боковых лепестков в д. Б, n – требуемое количество отсчетов окна.

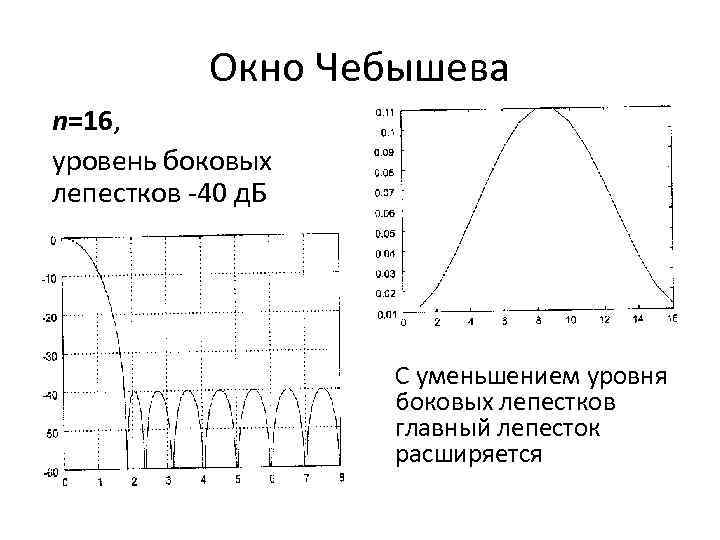Окно Чебышева n=16, уровень боковых лепестков -40 д. Б С уменьшением уровня боковых лепестков главный лепесток расширяется

Пример Рассмотрим пример использования весовых окон для улучшения ЧХ ФНЧ. Пусть требуется получить ФНЧ с идеальной прямоугольной частотной характеристикой. ИХ такого ФНЧ с частотой среза c описывается функцией

Пример Такая ИХ нереализуема. Физически реализуемая ИХ получается усечением и сдвигом, однако при этом возникает изрезанность ЧХ в полосе пропускания и большой уровень боковых лепестков в полосе непропускания.

Пример Если использовать для улучшения ЧХ весовую обработку, то для выборки объемом N=25 применение окна Хэмминга приводит к расширению главного лепестка ИХ примерно в два раза. Однако уровень боковых лепестков уменьшается до -40 д. Б, по сравнению с -12 д. Б для безвесовой обработки.

Пример Несколько меньшего расширения главного лепестка при том же уровне подавления боковых удается достичь при использовании окна Кайзера. Получаемая при использовании окна Кайзера частотная характеристика аппроксимируется выражением

Пример Зависимость достигаемого подавления боковых лепестков от коэффициента иллюстрируется таблицей: Окно Кайзера является оптимальным в том смысле, что при его умножении на последовательность конечной длины обеспечивается минимум энергии сигнала за пределами полосы прозрачности.