Корпоративные финансы Тема 6 Методы оценки капитальных финансовых

Корпоративные финансы Тема 6. Методы оценки капитальных финансовых активов (4 часа) Виталий Валерьевич Ковалев СПб. ГУ, кафедра теории кредита и финансового менеджмента тел. : (812) 272 -7821 сайт: http: //www. tcfm. ru В. Ковалев: СF-06

Определение (МСФО) Финансовый актив: (а) денежные средства; (б) договорное право требования денежных средств или другого ФА от другой фирмы; (в) договорное право на обмен финансовых инструментов с другой фирмой на потенциально выгодных условиях; (г) долевой инструмент другой компании. В. Ковалев: СF-06 2

Причины работы с FA: (а) выход на рынок капитала в поисках дополнительных источников; (б) хеджирование (т. е. страхование от возможных потерь); (в) спекулирование; (г) страховой запас высоко ликвидных активов В. Ковалев: СF-06 3

Базовые характеристики ФА Основные характеристики финансового актива как элемента рынка: { стоимость, цена, доходность, риск }. Четыре стоимостные характеристики: ценность, стоимость (Vt), цена (Pm), себестоимость. Vt - рассчитывается; Pm - декларируется. В. Ковалев: СF-06 4

Базовые характеристики ФА Ценность (маржинализм: оценка со стороны спроса, т. е. потребителя) и стоимость (классическая п/э: оценка со стороны предложения) близки. «Мера, в которой капитал и труд меняются друг на друга, составляет их ценность; мера же, в которой они обмениваются на деньги, составляет их цену» (Ж. -Г. Курсель-Сенель). В. Ковалев: СF-06 5

Стоимостные характеристики ФА (11) 1) Нарицательная стоимость – стоимостная оценка ФА, официально закрепленная за ним условиями эмиссии. 2) Цена размещения, или эмиссионная цена – цена, по которой ФА размещается, т. е. продается на первичном рынке. 3) Ликвидационная стоимость – стоимость, по которой, как полагают, можно продать некоторый актив (понуждающие факторы: есть/нет). В. Ковалев: СF-06 6

Стоимостные характеристики ФА – 2 4) Балансовая стоимость – стоимостная оценка ФА, исчисляемая по данным ББ. 5) Конверсионная стоимость – произведение Pm базисного актива (обычно это обыкновенная акция того же эмитента), лежащего в основе конвертации, и коэффициента конверсии. 6) Внутренняя (теоретическая, фундаментальная) стоимость – стоимость, исчисленная по DCF-модели. В. Ковалев: СF-06 7

Стоимостные характеристики ФА – 3 7) Выкупная цена – цена, по которой производится выкуп ФА эмитентом по истечении предусмотренного срока его жизни или до этого момента, если это предусмотрено условиями эмиссии. 8) Рыночная, или курсовая, цена – цена, по которой ФА продается на данном рынке. Pm зависит от конъюнктуры рынка, рыночной нормы прибыли, величина и динамика дохода, генерируемого активом, и др. В. Ковалев: СF-06 8

Стоимостные характеристики ФА – 4 9) Экс-дивидендная цена (ex-dividend price, ex -div) – цена акции, покупка по которой не дает права на получение последнего объявленного, но еще не выплаченного дивиденда (синоним – цена без дивиденда). В развитых экономиках: обычно акции начинают продаваться по цене ex-div за четыре дня до составления списка лиц, имеющих право на получение очередного дивиденда. В. Ковалев: СF-06 9

Стоимостные характеристики ФА – 5 10) Цена с включенным дивидендом (cumdividend price, cum-div) – цена акции, купив которую, акционер приобретает права на все дивиденды, включая последний объявленный, но не выплаченный дивиденд. ücum-div = ex-div + ближайший ожидаемый D. üПоявляется непосредственно перед выплатой D. üПереход от ex-div к cum-div – кратковременно. üЦена ex-div рассчитывается по DCF-модели и отражает долгосрочные ожидания. В. Ковалев: СF-06 10

Стоимостные характеристики ФА – 6 11) Справедливая стоимость (fair value) – характеристика объекта, определяющая его сравнительную значимость в потенциальных или фактических меновых операциях в условиях полной информированности участников сделки, их неангажированности и свободы в принятии решения. В. Ковалев: СF-06 11

Стоимостные характеристики ФА – 7 üСущественные условия сделки по справедливой стоимости: (а) независимость сторон; (б) осведомленность сторон; (в) невынужденный характер сделки; (г) доступность и публичность информации, на основе которой совершается сделка. Оценка: fair value = Pm, если есть рынок; fair value = оценочной стоимости, если рынка нет. В. Ковалев: СF-06 12

Логика финансовых операций Идея: сопоставление рыночной цены (Pm) и стоимости (Vt). Различия между Pm и ст Vt: ♧ Vt это расчетный показатель, а Pm– декларированный; ♧ в любой конкретный момент времени на данном рынке Pm однозначна, а Vt многозначна; ♧ Vt первична, а Pm вторична. В. Ковалев: СF-06 13

Логика финансовых операций – 2 Цена (Рm) – это то, что ты платишь, а стоимость (Vt ) – это то, что ты получаешь (цена очевидна, тогда как приобретенная стоимость неопределенна). Варианты соотношения: Рm > Vt или Рm < Vt или Р m = Vt В. Ковалев: СF-06 14

Логика оценки Vt – 1 Подходы к оценке FA: ♧ технократическая теория (Ч. Доу: идея поиска точки перелома тенденции); ♧ фундаменталистская теория (DCFмодель); ♧ теория «ходьба наугад» (Л. Башелье). Две типовые задачи: (1) оценка Vt, (2) оценка k. Фундаменталистский подход преобладает. В. Ковалев: СF-06 15

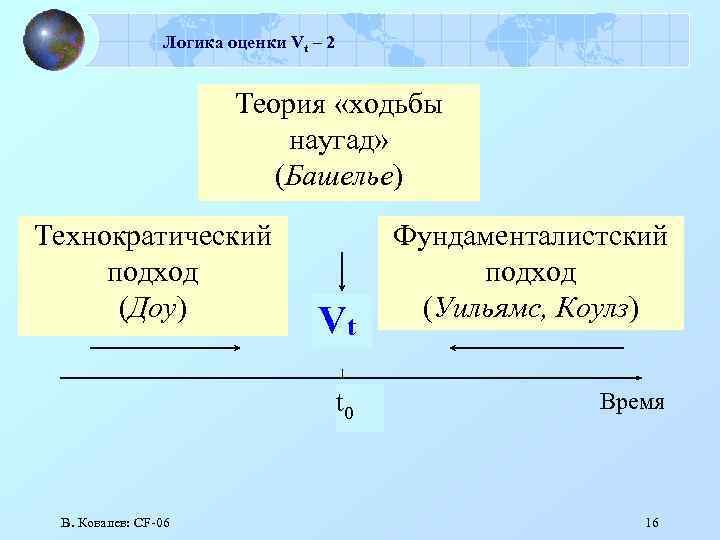Логика оценки Vt – 2 Теория «ходьбы наугад» (Башелье) Технократический подход (Доу) Vt t 0 В. Ковалев: СF-06 Фундаменталистский подход (Уильямс, Коулз) Время 16

Облигация – эмиссионная ценная бумага, закрепляющая право ее владельца на получение от эмитента облигации в предусмотренный в ней срок ее номинальной стоимости или иного имущественного эквивалента. Может предусматриваться выплата процента. Доходом по облигации являются процент и/или дисконт. В. Ковалев: СF-06 17

Облигация Свойства: (1) дает приоритетное право на получение процентов до начисления дивидендов; (2) дает приоритетное право перед собственниками на получение доли имущества при ликвидации фирмы; (3) не дает права ее владельцу на управление фирмой. В. Ковалев: СF-06 18

Облигация: стоимостные характеристики (1) нарицательная стоимость; (2) конверсионная стоимость; (3) внутренняя (теоретическая) стоимость; (4) выкупная цена; (5) рыночная цена. В. Ковалев: СF-06 19

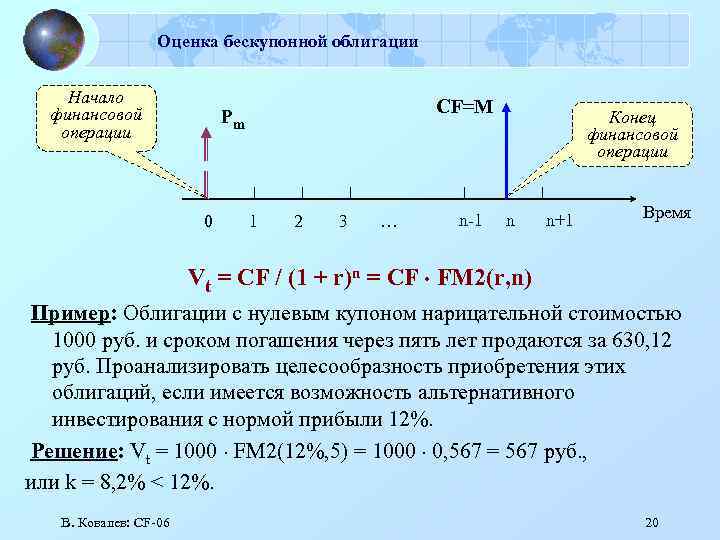Оценка бескупонной облигации Начало финансовой операции CF=M Pm 0 1 2 3 … n-1 Конец финансовой операции n n+1 Время Vt = CF / (1 + r)n = CF FM 2(r, n) Пример: Облигации с нулевым купоном нарицательной стоимостью 1000 руб. и сроком погашения через пять лет продаются за 630, 12 руб. Проанализировать целесообразность приобретения этих облигаций, если имеется возможность альтернативного инвестирования с нормой прибыли 12%. Решение: Vt = 1000 FM 2(12%, 5) = 1000 0, 567 = 567 руб. , или k = 8, 2% < 12%. В. Ковалев: СF-06 20

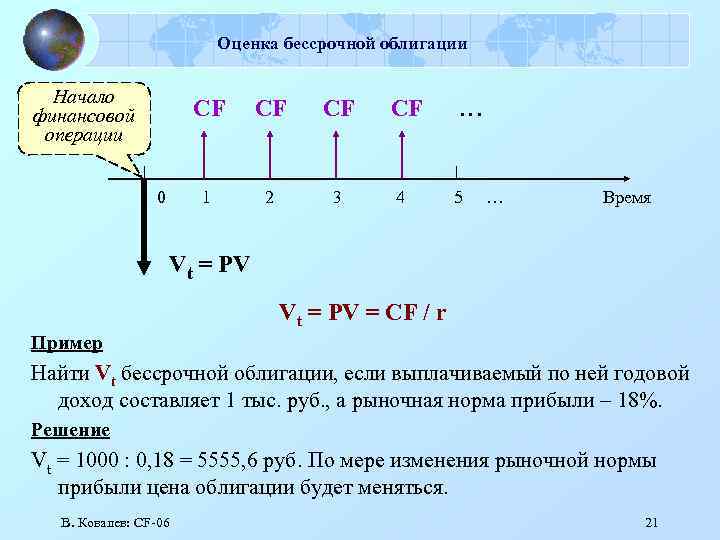Оценка бессрочной облигации Начало финансовой операции CF CF 1 0 CF 2 3 CF … 4 5 … Время Vt = PV = CF / r Пример Найти Vt бессрочной облигации, если выплачиваемый по ней годовой доход составляет 1 тыс. руб. , а рыночная норма прибыли – 18%. Решение Vt = 1000 : 0, 18 = 5555, 6 руб. По мере изменения рыночной нормы прибыли цена облигации будет меняться. В. Ковалев: СF-06 21

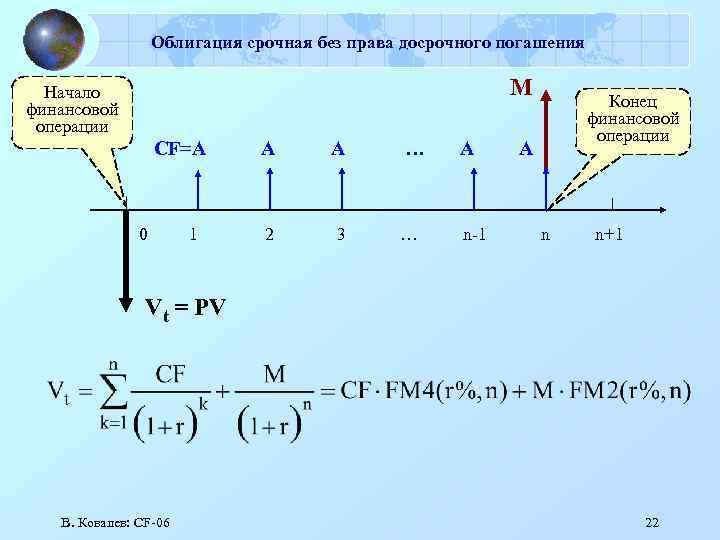Облигация срочная без права досрочного погашения M Начало финансовой операции CF=A 0 1 A A 2 3 … A … n-1 Конец финансовой операции A n n+1 Vt = PV В. Ковалев: СF-06 22

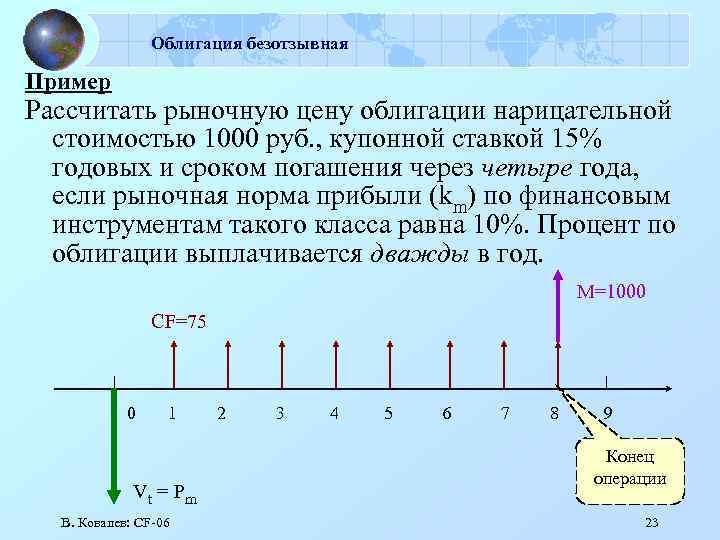Облигация безотзывная Пример Рассчитать рыночную цену облигации нарицательной стоимостью 1000 руб. , купонной ставкой 15% годовых и сроком погашения через четыре года, если рыночная норма прибыли (km) по финансовым инструментам такого класса равна 10%. Процент по облигации выплачивается дважды в год. M=1000 CF=75 0 1 Vt = P m В. Ковалев: СF-06 2 3 4 5 6 7 8 9 Конец операции 23

Облигация безотзывная (решение) (1) km = 10% Рm = Vt = 75 6, 463 + 1000 0, 677 = = 1162 руб. (2) km = 18% Vt = CF FM 4(9%, 8) + M FM 2(9%, 8) = = 75 5, 535 + 1000 0, 502 = 917 руб. (3) km = 15% Рm = Vt = 1000 руб. В. Ковалев: СF-06 24

Отзывная облигация Две дополнительные характеристики: (1) выкупная цена Pc, выплачиваемая в случае досрочного ее погашения; (2) срок защиты от досрочного погашения (первые m базисных периодов с момента эмиссии, в течение которых отзыв облигации с рынка запрещен). Две оценки Vt: досрочное погашение (1) мало вероятно; (2) весьма вероятно. В. Ковалев: СF-06 25

Отзывная облигация Базовая модель оценки где: n – число базисных периодов до окончания срока защиты; М – выкупная цена. В. Ковалев: СF-06 26

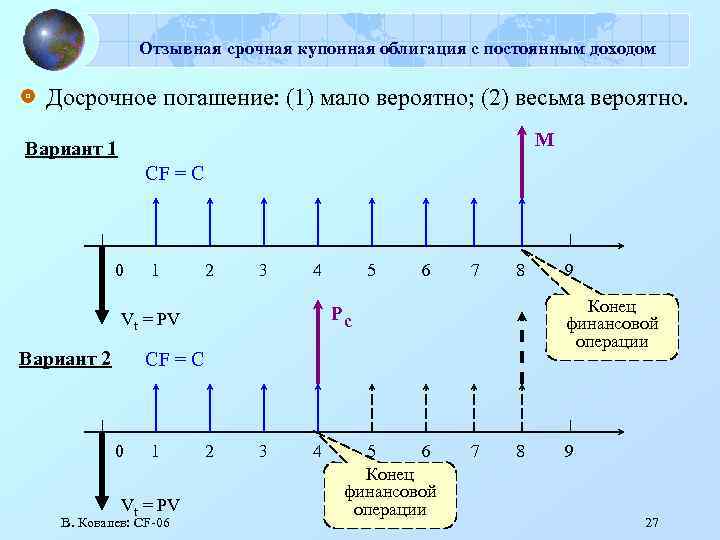Отзывная срочная купонная облигация с постоянным доходом Досрочное погашение: (1) мало вероятно; (2) весьма вероятно. M Вариант 1 CF = C 0 1 2 3 4 6 7 8 CF = C 0 1 Vt = PV В. Ковалев: СF-06 2 3 4 5 6 Конец финансовой операции 9 Конец финансовой операции Pc Vt = PV Вариант 2 5 7 8 9 27

Отзывная облигация (пример) Отзывная облигация номиналом 1000 долл. , с купонной ставкой 12% и ежегодной выплатой процентов будет погашена через 10 лет. На момент анализа облигация имеет защиту от досрочного погашения в течение пяти лет. В случае досрочного отзыва выкупная цена в первый год, когда отзыв становится возможным, будет равна номиналу плюс сумма процентов за год. Стоит ли приобрести эту облигацию, если ее текущая рыночная цена составляет 920 долл. , а приемлемая норма прибыли равна 14%? В. Ковалев: СF-06 28

Отзывная облигация (решение примера) (а) Оценка с позиции инвестора, который полагает, что вероятность досрочного погашения очень мала. Vt = 120 FM 4(14%, 10) + 1000 FM 2(14%, 10) = 120 5, 216 + 1000 0, 270 = 895, 92 долл. С позиции данного инвестора текущая цена облигации завышена, поэтому ее покупка нецелесообразна (Рm > Vt). В. Ковалев: СF-06 29

Отзывная облигация (решение примера) (б) Оценка с позиции инвестора, который полагает, что вероятность досрочного погашения достаточно велика. Vt = 120 FM 4(14%, 5) + 1120 FM 2(14%, 5) = 120 3, 433 + 1120 0, 519 = 993, 24 долл. С позиции данного инвестора текущая цена облигации занижена, поэтому ее покупка целесообразна (Рm < Vt). В. Ковалев: СF-06 30

Акции Долевые ценные бумаги – акции (привилегированные и обыкновенные). Привилегированная акция – бессрочный аннуитет: Vt = A / r (**) где r – ставка дисконтирования (внешний параметр). Обыкновенная акция: (1) дивиденды не меняются; (2) дивиденды возрастают с постоянным темпом прироста; (3) дивиденды возрастают с изменяющимся темпом прироста. В. Ковалев: СF-06 31

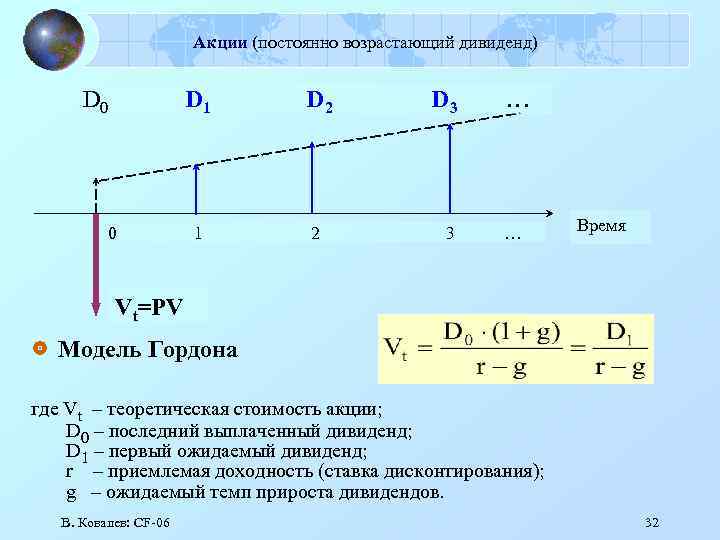Акции (постоянно возрастающий дивиденд) D 0 D 1 0 D 2 D 3 … 1 2 3 … Время Vt=PV Модель Гордона где Vt – теоретическая стоимость акции; D 0 – последний выплаченный дивиденд; D 1 – первый ожидаемый дивиденд; r – приемлемая доходность (ставка дисконтирования); g – ожидаемый темп прироста дивидендов. В. Ковалев: СF-06 32

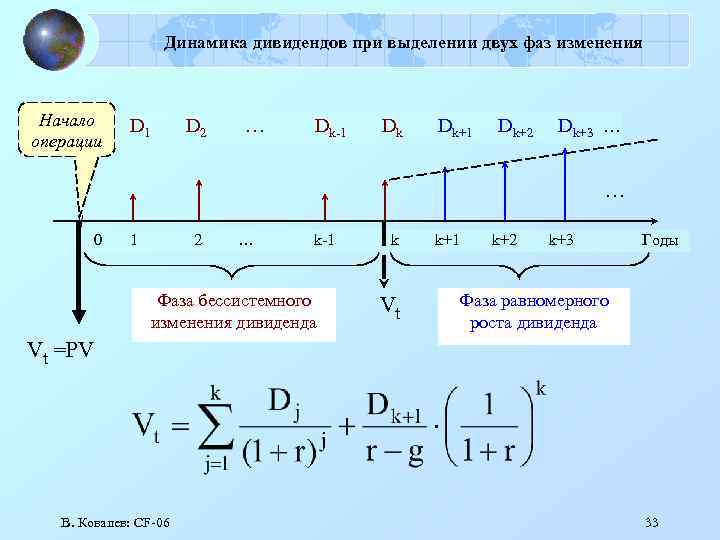Динамика дивидендов при выделении двух фаз изменения Начало операции D 1 D 2 … Dk-1 Dk Dk+1 Dk+2 Dk+3 … … 0 1 2 … k-1 Фаза бессистемного изменения дивиденда k Vt k+1 k+2 k+3 Годы Фаза равномерного роста дивиденда Vt =PV В. Ковалев: СF-06 33

Пример В течение последующих четырех лет компания планирует выплачивать дивиденды соответственно 1, 5; 2; 2, 6 долл. на акцию. Ожидается, что в дальнейшем дивиденд будет увеличиваться равномерно с темпом 4% в год. Рассчитать теоретическую стоимость акции, если rm = 12%. Решение Величина ожидаемого дивиденда пятого года будет равна: 2, 6 1, 04 = 2, 7 долл. Итак, в условиях эффективного рынка акции данной компании на момент оценки должны продаваться по цене, примерно равной 27, 62 долл. В. Ковалев: СF-06 34