Корень n-ой степени и его свойства І. Понятие

Корень n-ой степени и его свойства І. Понятие корня n- ой степени ІІ. Функции ІІІ. Свойства корня n- ой степени ІV. Преобразования иррациональных выражений

І. Понятие корня n-ой степени Определение 1. Корнем n -ой степени из неотрицательного числа а ( n= 2, 3, 4, 5, …) называют такое неотрицательное число, при возведении в степень n которого получается число а

Терминология √ — радикал n -показатель корня а — подкоренное число (выражение)

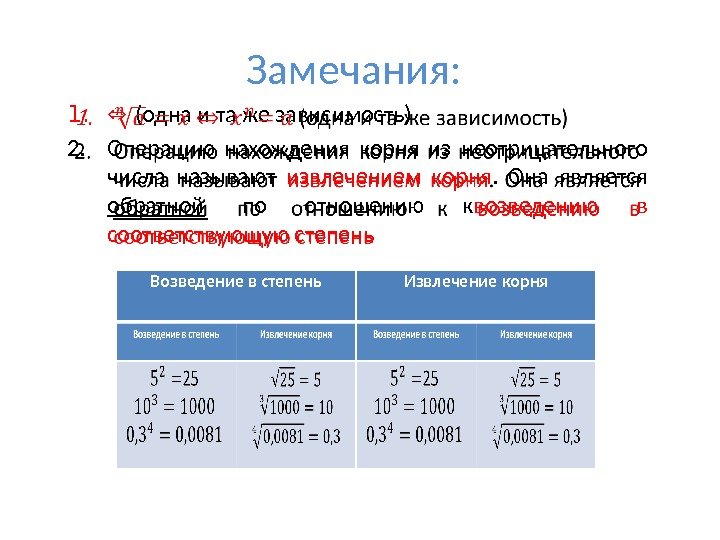Замечания: 1. ⇔ (одна и та же зависимость) 2. Операцию нахождения корня из неотрицательного числа называют извлечением корня. Она является обратной по отношению к возведению в соответствующую степень Возведение в степень Извлечение корня 25 Возведение в степень Извлечение корня

Определение 2. Корнем нечетной степени n из отрицательного числа а (n=3, 5, 7, …) называется такое отрицательное число, при возведении которого в степень n получается число а

Замечание: Корень четной степени имеет смысл только для неотрицательного подкоренного числа; корень нечетной степени имеет смысл для любого подкоренного числа

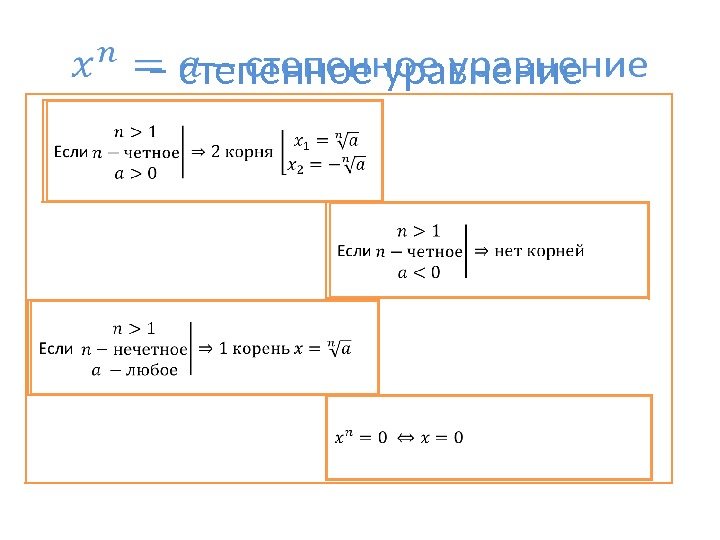– степенное уравнение Если

ІІ. Функции • Свойства функции • Если n — четное Если n — нечетное 1. Ни четная, ни нечетная 2. Возрастает на 3. Не ограничена сверху. Ограничена снизу 4. Непрерывна на 5. Выпукла вверх на 6. Дифференцируема на 1. Нечетная 2. Возрастает на 3. Не является ограниченной 4. Непрерывна на 5. Выпукла вверх на , выпукла вниз на 6. Дифференцируема на Если n — четное Если n — нечетное

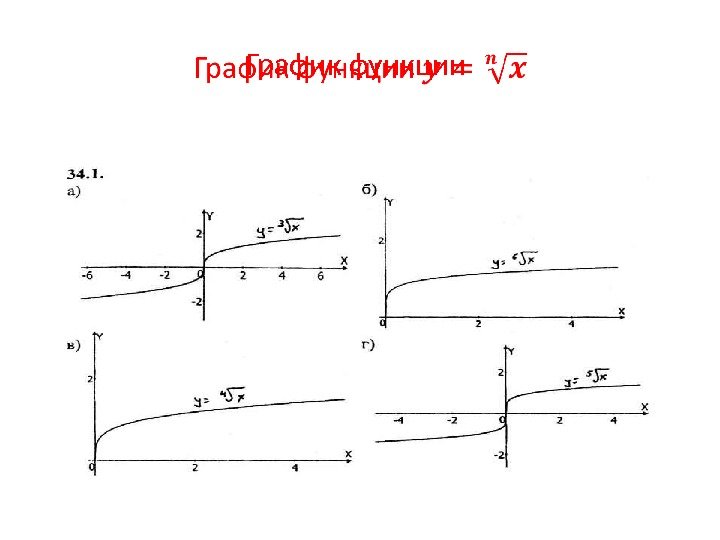График функции